秒杀共线向量求参的方法

江苏 范贤丽 王安寓

秒杀共线向量求参的方法

江苏 范贤丽 王安寓

最近正在复习《平面向量》，我在求解平面向量的题目过程中，发现了一种秒杀共线向量求参数值的方法．现整理成文，以飨读者．

一、秒杀解法的发现

【例1】已知向量a＝（1，0），b＝（2，1），若（ka－b）∥（a＋2b），则实数k＝________．

【分析】本题考查向量的坐标运算、向量共线的坐标公式，涉及简单的实数四则运算和解简单的方程．只须按条件代入坐标，计算即可．

上述求解过程中规中矩，没有一点可挑剔的．然而我觉得还是“多干活”了——实际上完全可以不计算坐标，就能观察出k的值．

二、秒杀解法之实例

常规解法与秒杀解法对比，常规解法多了许多计算，秒杀解法相应少了一些计算，甚至心算就行．

【类题1】已知向量a＝（1，0），b＝（2，1），若（ka－b）∥（a＋3b），则实数k＝________．

【秒杀解法】．

【类题2】已知向量a＝（1，2），b＝（0，1），设u＝a＋kb，v＝2a－b，若u∥v，则实数k＝________．

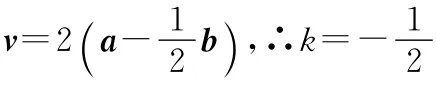
【类题3】已知向量a、b满足｜a｜＝1，｜b｜＝2，a与b的夹角为60°，记c＝2a＋b，设d＝ma－b，且d∥c，求实数m的值．

【秒杀解法】c＝－（－2a－b），∴m＝－2．

【类题4】已知向量a＝（2，1），b＝（0，－1），若（a－λb）∥a，则实数λ＝________．

【秒杀解法】a＝a－0·b，∴λ＝0．

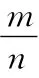
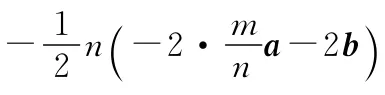
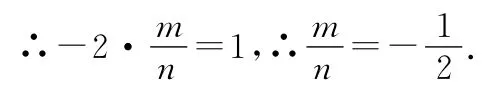
三、秒杀解法的理论依据

秒杀解法的理论依据是什么？其实就是共线向量定理和向量相等的充要条件．

我们通过以下题目给出解释．

【例2】已知a、b是不共线的两个向量，若8a＋kb与ka＋2b共线，则实数k＝________．

【常规解法】∵8a＋kb与ka＋2b共线，∴存在唯一实数λ，使得8a＋kb＝λ（ka＋2b），

∵a、b是不共线的两个向量，

从常规解法中，我们直观看到：所谓的共线向量，实际上就是通过变形，两个向量是若干倍的关系．对常规解法做简单变形，就得到秒杀解法．

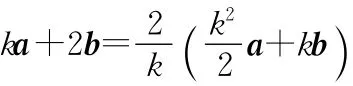
秒杀解法抛开了坐标计算和共线定理的直接应用，转化为考查两个基底的系数关系，本质上仍是共线向量定理的应用．

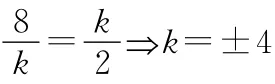
四、秒杀解法的应用范围

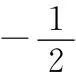
秒杀解法的本质是：通过观察找到了共线向量定理中的实数λ．如例1中，两个共线向量的关系是：a＋2b＝－2（ka－b）；例2中，两个共线向量的关系是：ka＋2b＝．共线向量定理中的实数λ一旦找到，求其他参数就轻而易举了．

五、秒杀解法思想迁移

以上，我们研究了向量a、b不共线（也就是能作为平面向量的基底），秒杀解法对向量a、b共线是否行得通呢？

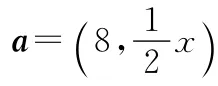
【分析】本题考查向量的坐标运算、向量共线的坐标公式，涉及简单的实数四则运算和解简单的方程．只须按条件代入坐标，计算即可．

上述解法是命题人希望我们采取的解法．其运算量稍大．实际上，我们可以通过向量与自身共线来简化运算．

【类题1】已知向量a＝（1，k），b＝（2，2），若（a＋b）∥2b，则实数k＝________．

我们从以上例3及其类题中看到：已知两个向量的线性和（差）共线，参数置入坐标中时，往往是两个向量共线．

六、对秒杀解法的反思

个人对秒杀解法的理解是：熟练掌握知识，才能反思出巧的解法．所谓的秒杀解法，实际上是省略了一些计算过程后呈现少的解法，是普通解法的升级版．其源头仍是普通解法，即通性通法．我们解完一道题后，要多做一些反思，可以是方法的反思，也可以是解题过程的反思．既可以考虑一题多解，也要考虑多题一解．本文是从多题一解的角度思考的，有不足之处，敬请指正．

（作者单位：江苏省南京市六合区实验高级中学）