“赵爽弦图”的数学文化背景考题赏析

山东 邹 龙

“赵爽弦图”的数学文化背景考题赏析

山东 邹 龙

1700多年前，赵爽绘制了极富创意的弦图（后人称之为“赵爽弦图”，如图1），采用“出入相补”原理使得勾股定理的成立不证自明．定理的证明体现出来的“形数统一”的思想方法，具有科学创新的重大意义．

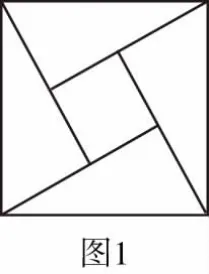
重视挖掘“赵爽弦图”所潜在的数学文化价值和应用功能，感受数学家的崇高品质及探究、解决数学问题的过程，进而体会中国古代数学的伟大贡献，增强爱国主义情怀，显得尤为必要．下面撷取几道以“赵爽弦图”为背景的高考题或模拟题，旨在抛砖引玉．

一、三角函数问题

【例1】2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图1）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cos2θ的值于________．

【分析】根据两正方形的面积分别求出两正方形的边长，根据小正方形的边长等于直角三角形的长直角边减去短直角边，利用三角函数的定义表示出5cosθ－5sinθ＝1，两边平方并利用同角三角函数间的基本关系及二倍角的正弦函数公式化简可得sin2θ的值，然后根据θ的范围求出2θ的范围即可判断出cos2θ的正负，利用同角三角函数间的基本关系由sin2θ即可求出cos2θ的值．

【点评】该考题取材2002年北京国际数学家大会（ICM2002）会标，题干大气，设问自然，流露出深刻的文化内涵．既巧妙地考查了三角的相关知识，又丰富了弦图的内涵．

【变式1】2002年8月在北京召开的国际数学家大会，会标是我国以古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图1）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，则sin2θ－cos2θ的值等于 （ ）

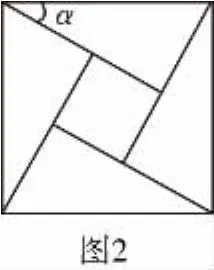
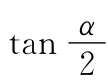
【解】由题意知，小正方形的边长为2，大正方形的边长为10．设直角三角形中较小边长为x，

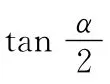
二、向量问题

【分析】首先求出cosθ，然后利用向量投影的定义求解．

【解】由题意知大正方形的边长为1，小正方形的边长为

【点评】本题以“赵爽弦图”为背景考查了三角恒等变换和平面向量的投影的概念和求法．

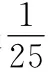
三、数列问题

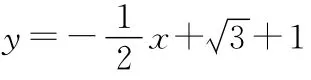
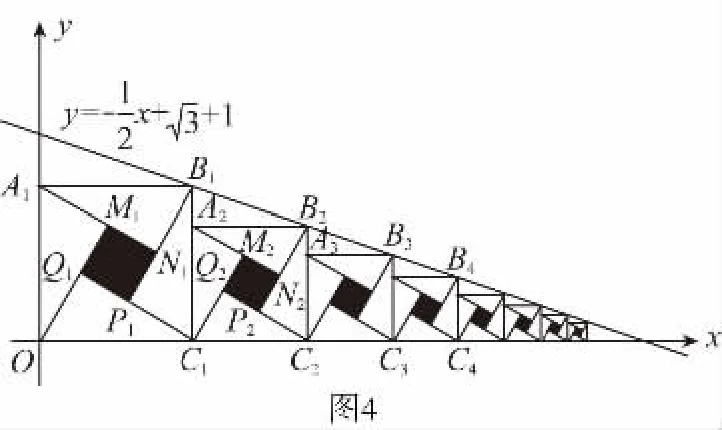
【分析】利用直角三角形两条直角边的差求出第一个正方形的边长，依次求出第二个、第三个小正方形的边长，归纳总结得到第n个小正方形的边长，则第n个阴影正方形的面积可求．

【解】因为每四个全等直角三角形都组成1个大正方形和1个小正方形，把这样的一个组合称为一组．

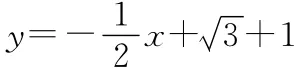
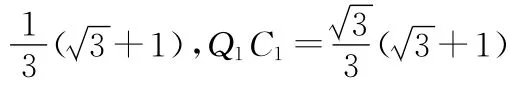
接下来的每一组大正方形的边长都会逐渐变小，但是成一定规律的．

【点评】本题将“赵爽弦图”置入平面直角坐标系中，使“赵爽弦图”与一次函数、数列的函数特性、数列和的求法相结合，构思新颖，设计巧妙，给人以美的享受．解答的关键在于通过求解前几个小正方形的边长，总结出小正方形边长的关于n的函数表达式．本题对考生的要求较高，要正确解决本题，考生要有扎实的基础知识，较强的分析问题、解决问题的能力和归纳推理能力，充分考查了考生的数学素养．

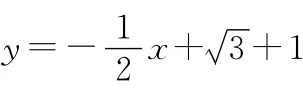
（作者单位：山东省泰安英雄山中学）