赏析由数学家引发的数学题

江苏 王佩其

赏析由数学家引发的数学题

江苏 王佩其

数学的发展，离不开历代数学家的贡献．当数学文化走进数学高考时，由数学家引发的数学题便应运而生，这些试题集数学文化与数学知识于一体，已成为当今高中数学一道亮丽的风景．我们一起来赏析几例．

一、数学家与函数问题

【狄利克雷】约翰·彼得·古斯塔夫·勒热纳·狄利克雷（Johann Peter Gustav Lejeune Dirichlet，勒热纳·狄利克雷是姓，1805年2月13日－1859年5月5日），德国数学家．他是解析数论的奠基者，也是现代函数概念的定义者．

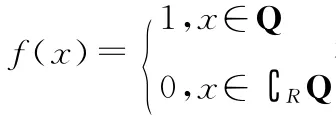
①f（f（x））＝0；

②函数f（x）是偶函数；

③任取一个不为零的有理数T，f（x＋T）＝f（x）对任意的x∈R恒成立；

④存在三个点A（x1，f（x1）），B（x2，f（x2））C（x3，f（x3）），使得△ABC为等边三角形．其中真命题的个数是 （ ）

A．1 B．2

C．3 D．4

【解析】当x为有理数时f（x）＝1，当x为无理数时，f（x）＝0，

∴当x为有理数时，f（f（x））＝f（1）＝1；

当x为无理数时，f（f（x））＝f（0）＝1，

即不论x是有理数还是无理数，均有f（f（x））＝1，故①不正确．

∵有理数的相反数还是有理数，无理数的相反数还是无理数，

∴对任意x∈R，都有f（－x）＝f（x），故②正确．

③若x是有理数，则x＋T也是有理数；若x是无理数，则x＋T也是无理数，∴根据函数的表达式，任取一个不为零的有理数T，f（x＋T）＝f（x）对x∈R恒成立，故③正确．

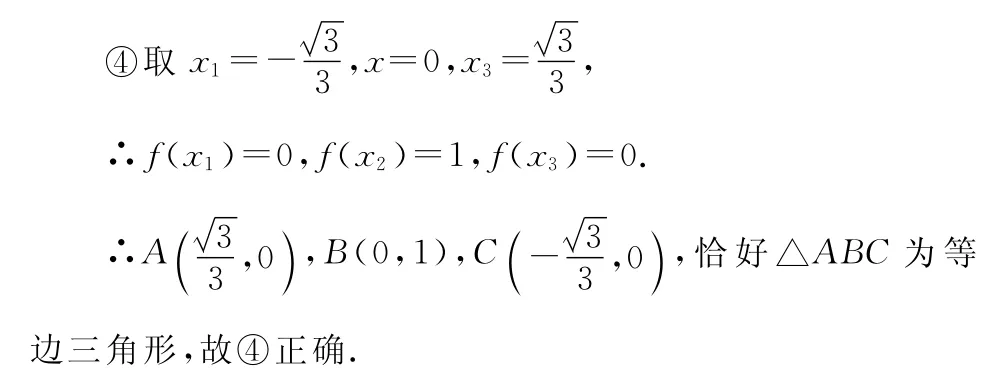
综上，应选C．

【评注】本题主要考查分段函数的基本性质．借助狄利克雷函数考查了分段函数的函数值的计算、分段函数周期性与奇偶性及其分段函数的应用．题干新颖，难度一般．

二、数学家与数列问题

【斐波那契】比萨的列奥纳多，又称斐波那契（Leonardo Pisano，Fibonacci，Leonardo Bigollo，1170年－1250年），意大利数学家，是西方第一个研究斐波那契数列的人，并将现代书写数和乘数的位值表示法系统引入欧洲．

【例2】意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和，人们把这样的一列数所组成的数列｛an｝称为“斐波那契数列”，该数列是一个非常美丽、和谐的数列，有很多奇妙的性质，比如：随着项数的增加，前一项与后一项的比值越逼近黄金分割0．6180339887．若把该数列｛an｝的每一项除以4所得的余数按相对应的顺序组成新数列｛bn｝，在数列｛bn｝中第2016项的值是________．

【解析】由题意得，数列1，1，2，3，5，8，13，…，除以4所得的余数分别为1，1，2，3，1，0，1，1，2，3，1，0，…，即新数列｛bn｝是周期为6的周期数列，所以b2016＝b336×6＝a6＝0．

【评注】本题主要考查了数列的综合应用问题，其中解答中涉及数列的递推关系式的应用、数列的周期性的应用等知识点的考查，着重考查了学生分析问题和解答问题的能力，试题有一定的难度，属于中档试题．本题的解答中仔细审题，根据数列的递推关系得出数列为周期数列是解答的关键．

三、数学家与解析几何问题

【欧拉】莱昂哈德·欧拉（Leonhard Euler，1707年4月15日－1783年9月18日），瑞士数学家、自然科学家．欧拉是18世纪数学界最杰出的人物之一，他不但为数学界做出贡献，更把整个数学推至物理的领域．他是数学史上最多产的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学、变分法等课本，《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作．

【例3】数学家欧拉在1765年提出定理：三角形的外心、重心、垂心，依次在同一条直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线后人称为三角形的欧拉线．已知△ABC的顶点A（2，0），B（0，4），若其欧拉线方程为x－y＋2＝0，则顶点C的坐标是________．

即x－2y＋3＝0．

∴△ABC的外心为（－1，1）．

则（m＋1）2＋（n－1）2＝32＋12，

整理得m2＋n2＋2m－2n＝8，②

联立①②，得m＝－4，n＝0或m＝0，n＝4．

当m＝0，n＝4时B，C重合，舍去．

∴顶点C的坐标是（－4，0）．

【评注】本题引进欧拉线，增强了试题的数学文化．本题主要考查直线方程，利用方程思想求点的坐标，难度中等．

四、数学家与立体几何问题

【阿基米德】阿基米德（公元前287年—公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯、牛顿并列为世界三大数学家．

【例4】如图是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等．相传这个图形表达了阿基米德最引以自豪的发现“圆柱容球定理”．我们来重温这个伟大发现：

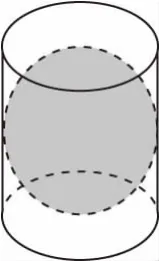
（1）求圆柱的体积与球的体积之比；

（2）求圆柱的表面积与球的表面积之比．

【解析】（1）设圆柱的高为h，底面半径为r，求的半径为R，

【评注】本题考查球与圆柱的内切及体积和表面积的算法，难度不大，但必须记住有关球体与柱体的体积与表面积的计算公式．

五、数学家与算法初步问题

【刘徽】刘徽（约公元225年—295年），汉族，山东邹平县人，魏晋期间伟大的数学家，中国古典数学理论的奠基人之一．是中国数学史上一个非常伟大的数学家，他的杰作《九章算术注》和《海岛算经》，是中国最宝贵的数学遗产．

【例5】公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3．14，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n值为 （ ）

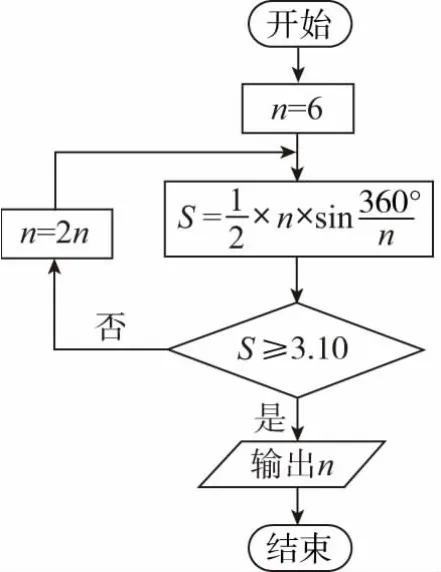
A．12 B．24 C．48 D．96

【解析】由程序框图，n，S值依次为：n＝6，S＝2．59808；n＝12，S＝3；n＝24，S＝3．10583，此时满足S≥3．10，输出n＝24．应选B．

【评注】本题考查程序框图．解题时要注意两种循环结构的区别，这也是容易出错是地方：当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．

六、数学家与合情推理问题

【伯努瓦·曼德尔布罗】伯努瓦·曼德尔布罗，世界“分形几何之父”，1924年11月20日出生于波兰，童年时随家人移居法国，后来在美国担任耶鲁大学名誉教授．2010年10月14日，伯努瓦·曼德尔布罗在美国马萨诸塞州剑桥辞世，享年85岁．

【例6】分形几何学是数学家伯努瓦·曼德尔布罗在20世纪70年代创立的一门新的数学学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照如图甲所示的分形规律可得如图乙所示的一个树形图：记图乙中第n行白圈的个数为an，则：

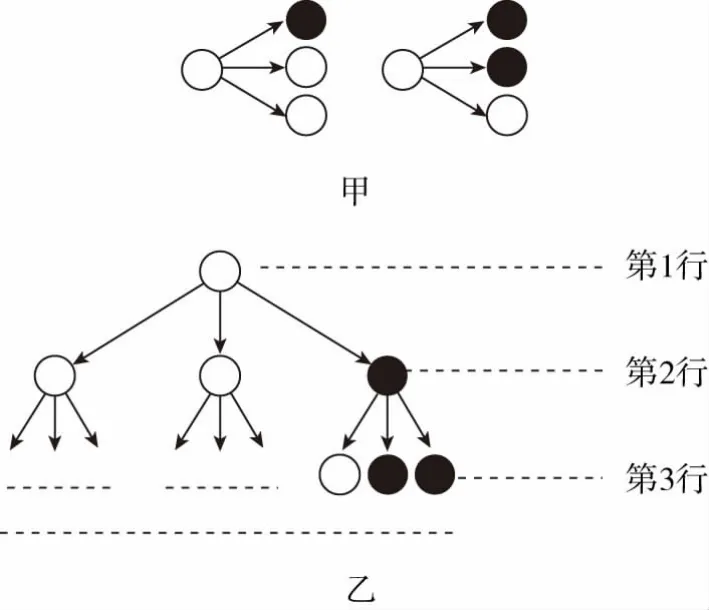
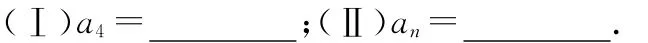
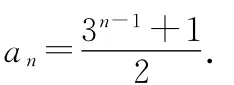
【评注】本题主要考查了与数列有关的归纳推理，归纳推理的一般步骤：（1）通过观察个别情况发现某些相同的性质；（2）从已知的相同性质中推出一个明确的表达的一般性的命题，正确理解归纳推理的步骤是解答此类问题的关键，本题的解答中，根据题设中分形规律，则可得第一行为（1，0）；第二行为（2，1）；第三行为（5，4）；第四行为（14，13），各行白圈数乘以2，分别是2，4，10，28，82，…，即1＋1，3＋1，9＋1，27＋1，81＋1，…，即可得出an的表达式．

七、数学家与数学猜想问题

【科拉茨】洛萨·科拉茨（Lothar Collatz，1910．7．6－1990．9．26），德国数学家，于1937年提出最早提出“3N＋1猜想”．

（1）如果n＝2，则按照上述规则施行变换后的第8项为________．

（2）如果对正整数n（首项）按照上述规则施行变换后的第8项为1（注：1可以多次出现），则n的所有不同值的个数为________．

则n的所有可能取值为2，3，16，20，21，128，共6个．

【评注】数学猜想是推动数学理论发展的强大动力．数学猜想是数学发展中最活跃、最主动、最积极的因素之一，是人类理性中最富有创造性的部分．在数学试题中引入数学猜想，并让考生沿着数学猜想的思路探究有关新的问题，不仅考查了考生的探究能力，而且能让试题更具有数学味儿．

（作者单位：江苏省太仓市明德高级中学）