基于改进小波神经网络的动车组牵引电机故障趋势预测
2017-08-08刘海生
刘 峰,刘海生
(北京交通大学 计算机与信息技术学院,北京 100044)
基于改进小波神经网络的动车组牵引电机故障趋势预测
刘 峰,刘海生
(北京交通大学 计算机与信息技术学院,北京 100044)
针对小波神经网络在多维输入情况下易于陷入局部极小值、收敛速度慢的弱点,引入Levenberg Marquardt(LM)算法优化小波神经网络,解决传统小波神经网络收敛速度慢的问题。基于传统小波神经网络和LM算法改进的小波神经网络分别建立预测模型,用于动车组牵引电机的故障趋势预测,通过MATLAB软件对两种预测模型的训练过程进行了数值仿真,仿真实验结果表明改进小波神经网络建立的故障预测模型提高了小波神经网络的预测精度,同时加快了神经网络的收敛速度,是一种有效的预测模型。
小波神经网络;LM算法;动车组牵引电机;故障趋势预测
0 引言
近年来我国高速铁路动车组进入大规模建设时期,投入运营的动车组数量不断增加,动车组监测数据也不断的增长。牵引电机为动车组提供动力,在运行过程中承受各种电磁交变应力的作用,易导致牵引电机出现各种电气故障和机械故障,牵引电机的正常运行对动车组的安全起着至关重要的作用。因此利用这些不断积累的动车组监测数据,对牵引电机进行故障趋势预测,具有十分重要的意义。
小波神经网络用小波函数代替BP神经网络隐含层节点的激励函数,通过映射变换建立起小波变换与网络系数之间的连接,广泛应用于设备的故障诊断和故障趋势预测。但传统小波神经网络的学习训练算法一般为梯度下降法,在多维输入情况下有易于陷入局部极小值、收敛速度慢的弱点[1],无法满足动车组进行实时故障预测的要求。本文提出一种基于LM算法优化小波神经网络的方法,并应用于动车牵引电动机的故障趋势预测。实验结果表明,经过改进的小波神经网络不仅迭代次数少,而且收敛精度也得到了较大的提高。
1 小波神经网络及改进
1.1 小波神经网络
1992年,法国信息科学研究机构的Qinghua Zhang等人提出了小波神经网络的概念和算法[2]。小波神经网络是一种基于小波变换理论而构造的前馈神经网络,具有较强的函数逼近能力和较快的收敛速度,其主要可分为松散型和紧密型两种类型。本文采用紧密型结构来构造小波神经网络,其基本思想是将常规小波神经网络隐含层节点的激励函数用小波函数代替,在网络训练过程中逐步更新神经元间的连接权值、神经元的阈值及小波函数的伸缩因子和平移因子。3层前馈网络能以任意精度逼近一个非线性映射[3],因此本文采用3层小波神经网络用于构造动车组牵引电机的故障趋势预测模型。
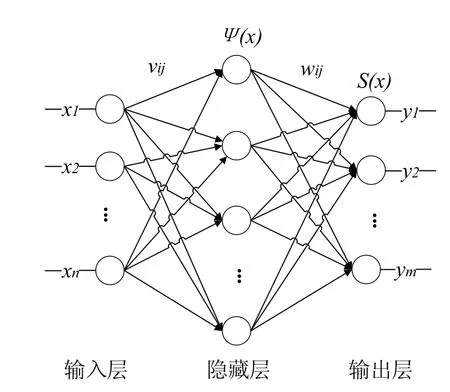
图1 三层小波神经网络结构
图1为3层小波神经网络的网络结构图,其中输入层有n个神经元,隐含层有k个神经元,输出层有m个神经元,输入层和输出层的神经元个数根据实际要求确定,隐含层神经元数参考经验公式表示输人层的第i个神经元与隐含层的第j个神经元的连接权值,wij表示隐含层的第i个神经元与输出层的第j个神经元的连接权值。设网络输入变量实际输出变量期望输出变量则隐含层输出的计算公式为:
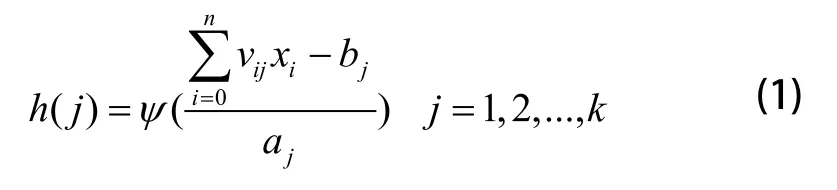
其中,h(j)为隐含层第j个节点的输出值,Ψ(x)为小波函数,bj为小波函数的平移因子,aj为小波函数的伸缩因子,v0j是第j个隐含层节点阈值(相应的x0=-1),隐含层神经元的激励函数常采用Morlet小波[4]:
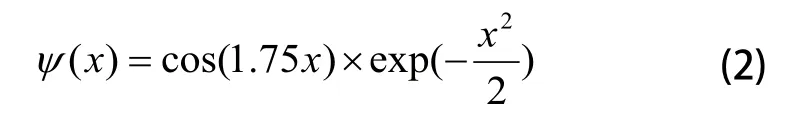
输出层神经元则采用sigmoid函数作为激励函数:
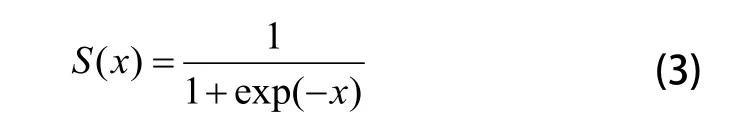
设w0j是第j个输出层节点阈值,则小波神经网络输出层的计算公式为:
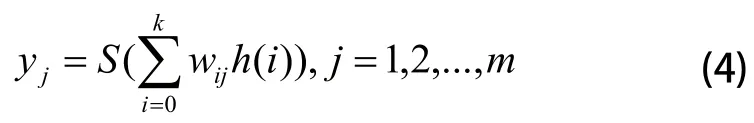
传统小波神经网络多采用梯度下降法修正网络的权值和小波函数的参数。梯度下降法是一阶最优化算法,核心思想是以目标函数的负梯度方向为搜索方向,通过每次迭代使待优化的目标函数逐步减小。这种搜索是一种贪心算法的过程,只考虑目标函数在迭代点的局部性质。其中学习速率选择过大或过小会导致网络训练过慢或震荡发散,因此通常会在梯度下降法的基础上附加动量因子加速算法收敛[5],使小波神经网络预测输出不断逼近期望输出。给定样本集根据梯度下降法定义误差目标函数:
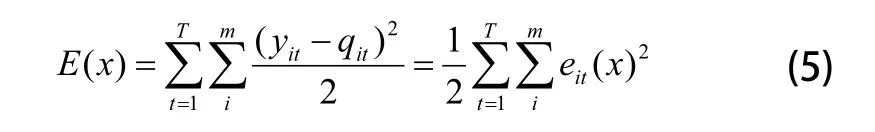
基于上述目标函数进行误差反向传播,使权值沿误差函数的负梯度方向改变,利用梯度下降法调整优化小波神经网络的参数;
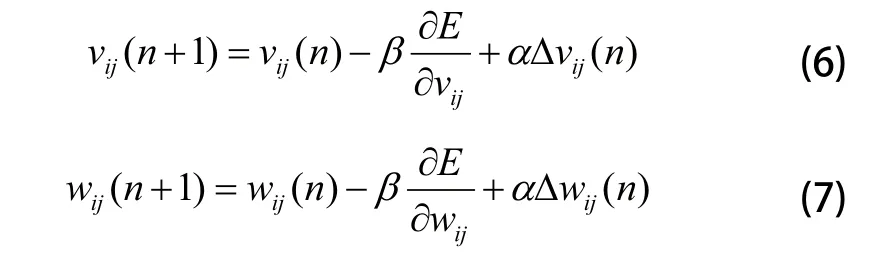
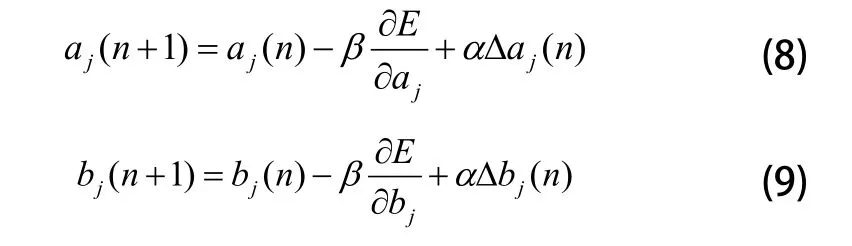
其中,t为迭代次数,β为学习速率,α为动量因子。
1.2 LM算法改进的小波神经网络
1.2.1 LM算法
传统的小波神经网络算法采用梯度下降法进行误差反向传播,参数沿着与误差梯度相反的方向移动,使误差函数达到极小值。附加动量因子记忆上次迭代的变化方向,可以采用较大的学习速率系数以提高学习速度,但是参数调整优化过程依然线性收敛,相对速度依然较慢。LM算法是一种利用标准数值优化技术的快速算法,具有高斯牛顿法的局部收敛性和梯度下降法的全局特性,在局部搜索能力上强于梯度下降法[6]。
LM算法基本思想是先沿着负梯度方向进行搜索,然后根据牛顿法在最优值附近产生一个新的理想的搜索方向。LM算法具有二阶收敛速度,迭代次数很少,可以大幅度提高收敛速度和算法的稳定性,避免陷入局部最小点的优点。设x(n)表示第n次迭代的小波神经网络的参数所组成的向量,新的参数向量x(n+1)可根据下面的规则求得:
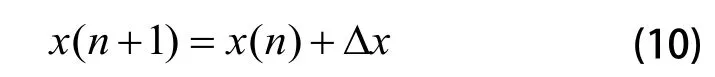
按式(5)定义的误差目标函数,对于小波神经网络的参数有Jacobian矩阵:
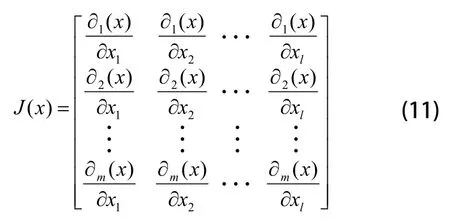
LM算法改进小波神经网络的权值修正量为:

其中μ>0是比例系数,I是单位矩阵。当μ=0时,LM算法转化为具有近似高斯牛顿法。当μ较大时,LM算法接近小步长的梯度下降法。
1.2.2 LM算法改进小波神经网络的计算步骤
1)给出网络训练误差允许值ε及网络最大训练次数M,一般选定ε=0.0000001,M=5000次,初始化系数μ0和β,且令n=0,μ=μ0。
2)计算网络输出Y(m)及误差目标函数E(n)。
3)计算Jacobian矩阵。
4)计算权值修正量∆x(k)。
5)若E(n)<ε或n>M,转至步骤7),否则以x(n+1)为权重,计算误差E(n+1)。
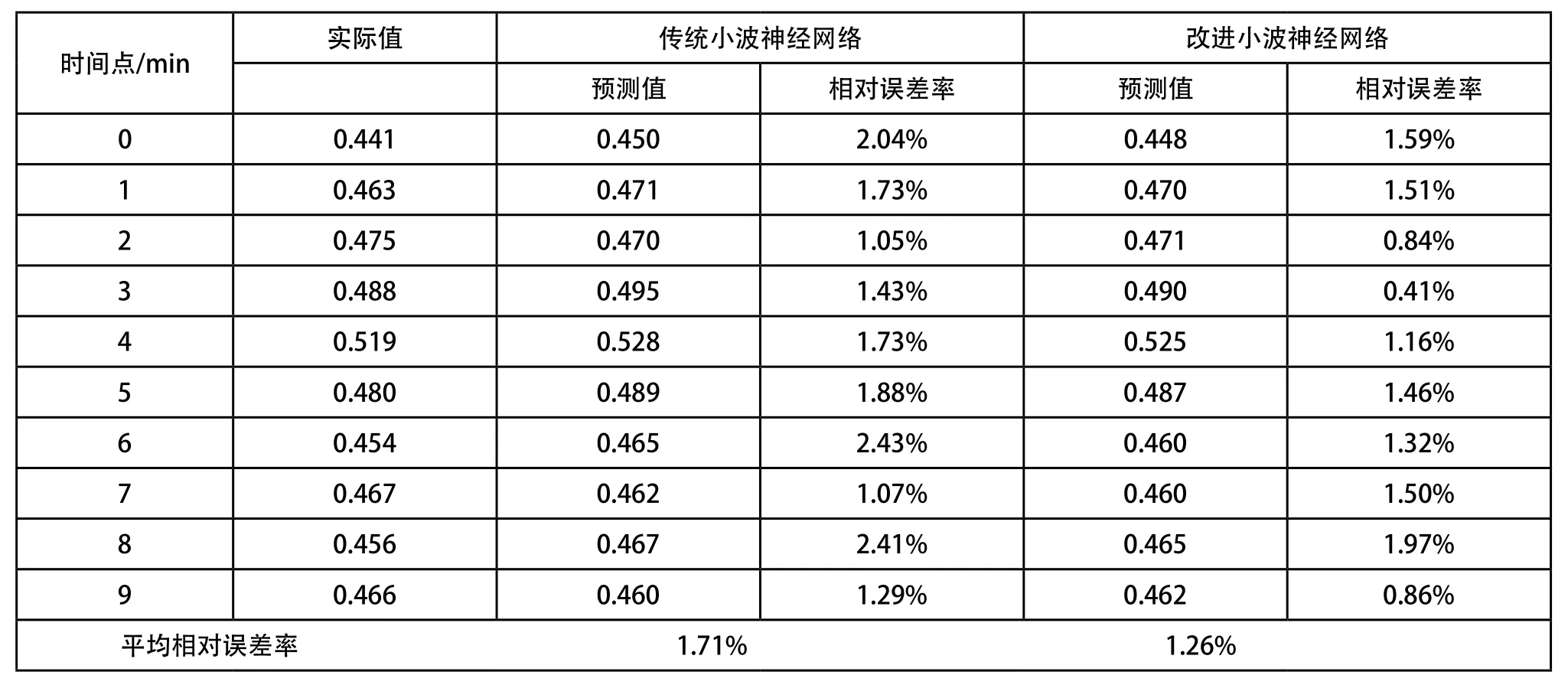
6)若E(n+1) 7)停止。 故障预测就是对装备的未来性能给出定量的评价、分析[7]。动车组牵引电机故障趋势预测模型以动车组牵引电机当前的运行状态为起点,对未来任务段内其运行状态的变化给出预测,以便于根据已知的结构特性、功能参数、服役条件及运行历史(包括运行记录和以往故障及修复的记录),对动车组牵引电机可能出现的故障进行预报、分析和判断[8]。 2.1 动车组电机预测的特点 动车组牵引电机固定在动车转向架上,与周围环境密切接触,工作环境相对恶劣,工作强度较大,导致动车组牵引电机易发生各种电气故障和机械故障,其故障趋势预测也具有一下特点: 1)实时性要求。动车组牵引电机的运行状态对于动车组的正常运行具有重要意义,其监控数据频率是分钟级别的,这就要求预测模型必须有较快的运算速度。 2)多因素相互影响。动车组牵引电机工作环境恶劣,其运行状态受环境影响,各种运行状态指标之间也存在相互影响,对其故障趋势的预测必须考虑多因素。文献[9]进行了发电机组振动多因素预测,并通过实验比较说明随机时间序列受多种因素影响时,将这些影响因子也作为网络的输入,综合考虑网络预测结果更好。 3)短时运行环境相对稳定。动车组短时内运行速度、运行环境温度等相对变化较稳定。 2.2 动车组电机故障趋势预测 针对动车组电机故障预测特点,建立时间序列上的动车组电机多因素滚动故障趋势预测模型,利用过去一段时间的监测值预测未来的一段时间内动车组牵引电机的状态。将动车组电机的历史状态数据编辑整理成时间序列,用每次单步预测模型的预测值替换下一步预测模型中输入层时间最老的一个值,依次迭代,得到未来一段时刻的预测值。由于动车组电机短时运行环境相对稳定,对动车组电机的运行状态产生影响的其他多因素取最近时刻的状态值。 其中(x1,x2,…,xn,yn,…,zn)、(x2,x3,…,xn+1,yn+1,…,zn+1)和(xk-n,xk-n+1,…,xk-1,yk-1,…,zk-1)为训练样本输入,模型训练收敛后,输入样本(xk-n+1,xk-n+2,…,xk,yk,…,zk)预测xk+1时刻的值。依次类推得到期望的预测时间序列。 使用上海铁路局提供的动车组牵引电机监控数据,分别建立传统小波神经网络和改进小波神经网络的预测模型,基于牵引电机的轴承温度、列车速度、环境温度和定子温度4个因素对定子温度做预测,在MATLAB下验证改进神经网络建立的预测模型的优越性。实验1通过比较两个模型的迭代次数,验证改进模型实时预测性能的优越性;实验2通过比较两个模型的预测结果,验证改进模型预测精度的优越性。 3.1 数据归一化处理 小波神经网络的输入变量具有不同的物理意义和不同的量纲,归一化之后的数据都在[0,1]之间变化,从而使网络训练中各输入分量有同等重要的地位。同时输出层小波函数选用Sigmoid函数,该函数输出在0~1之间,因此必须对数据归一化处理才能用于预测问题。将输入输出数据变换为[0,1]区间的值常用以下变换式: 3.2 实例分析 现有来源于上海铁路局的动车组牵引电机监测数据,是国内某段动车组2016年7月和8月共62天的监控数据,数据时间单位是分钟,选用7月1日这一天5个小时共300组数据做实验验证。前280组数据做模型训练,最后20组数据分别用于实验1和实验2。其中前10组数据用于实验1,后10组数据用于实验2。利用常规小波神经网络和改进的神经网络分别建立多因素滚动预测模型,基于牵引电机的轴承温度、列车速度、环境温度和定子温度4个因素对定子温度做预测,从预测的精度和模型训练的迭代次数两个方面,比较两种预测模型的性能。 根据动车组牵引电机的特性设计小波神经网络,确定输入层节点数16,其中13个节点是动车组电机的定子温度时间序列,其他3个节点分为列车速度、环境温度和定子温度,输出层节点1个,隐含层节点4个,即本案例网络拓扑结构为16:4:1。初始化神经网路参数学习率为0.5,网络权值选定为0.5~+0.5之间的一组随机数,小波函数选用morlet函数,系统误差选定为0.0000001,最大迭代次数为5000次。 分别使用传统小波神经网络和改进小波神经网络建立的牵引电机故障预测模型,采用相同的280样本数据对预测模型进行训练。实验1使用相同的10组数据测试上述训练完成的预测模型,误差曲线如图2和图3所示。 图2 传统小波神经网络误差迭代曲线 图3 改进小波神经网络误差迭代曲线 从图2和图3可以看出,改进小波神经网络的收敛速度更快,网络迭代次数更少,改进小波神经网络迭代41次收敛,常规小波神经网络迭代94次收敛,改进小波神经网络的收敛速度提高了56%。迭代次数的减少,意味着改进小波神经网络建立的预测模型在预测实时性上更好。 实验2使用训练完成的预测模型预测未来电机定子温度的10组数据,预测结果如图4和图5所示,通过观察预测拟合曲线可以发现,预测变化趋势与实际值基本一致,因此可以用训练好的网络来预测动车组牵引电机的定子温度,并对预测结果进行分析。 图4 传统小波神经网络预测结果 图5 改进小波神经网络预测结果 采用相对误差率分析预测结果,其计算公式为: 通过预测结果对照表1发现,用改进小波神经网络建立的预测模型平均误差率为1.26%,传统小波神经网络建立的预测模型为1.71%,改进模型预测的准确定更好。 本文采用小波神经网络用于动车组牵引电机的故障 【】【】趋势预测,通过预测牵引电机状态变化,反应其故障变化趋势。利用LM算法改进小波神经网络,分别建立改进小波神经网络和传统小波神经网络的电机故障趋势预测模型,通过以上实验可以得到以下结论: 表1 动车组牵引电机预测情况表 1)采用改进小波神经网络建立的预测模型,网络训练迭代次数更少,网络收敛速度更快,预测的实时性更好。 2)采用改进小波神经网络建立的预测模型,预测的准确性也得到了一定的提高。 因此,基于改进小波神经网络建立的动车组牵引电机多因素滚动故障预测模型具有更好的先进性和实用性,是一种有效的动车组牵引电机预测方法。 [1] 杨国为,王守觉,闫庆旭.分式线性神经网络及其非线性逼近能力研究[J].计算机学报,2007,30(2):189-199. [2] Zhong Shisheng.Continuous wavelet process neural network and its application[J].Neural Network World,2007,17(5):483-495. [3] 阎平凡,张长水.人工神经网络与模拟进化计算[M].北京:清华大学出版社,2000. [4] 涂远,杜建江,王涛.压电类智能层合结构的ANSYS仿真分析[J].广西大学学报(自然科学版),2005,30(4):288-292. [5] J. L. Guardado. A comparative study of neural network efficiency in power transformers diagnosis using dissolved gas analysis[J].IEEE Transactions on Power Delivery,2001,16(4):643-647. [6] McKeown, John J. Some numerical aspects of the training problem for feed-forward neural nets[M].Elsevier Science Ltd.,1997,10(9):1455-1463. [7] 陈明,顾幸生.故障模糊预测模型研究[J].系统仿真技术,2005,1(2):74-78. [8] Himmelblau DM. Fault detection and diagnosis in chemical and petrochemical process[M].Amsterdam: Elsevier Press,1978. [9] AS Willsky. A survey of design methods for failure detection in dynamic systems[J].Automatica,1975,12(6):601-611. Fault trend prediction of EMU traction motor based on improved wavelet neural network LIU Feng, LIU Hai-sheng U269 :A 1009-0134(2017)07-0015-05 2017-05-02 国家科技部“863”项目-高速铁路动车组全生命周期数据集成化管理平台技术研究项目(K15B200011);国家科技支撑计划项目:面向高铁列车高效生产的新一代认知型制造执行系统研究与应用示范(2015BAF08B02) 刘峰(1961 -),男,北京人,教授,博士,研究方向为计算机软件。2 动车组牵引电机故障趋势预测模型
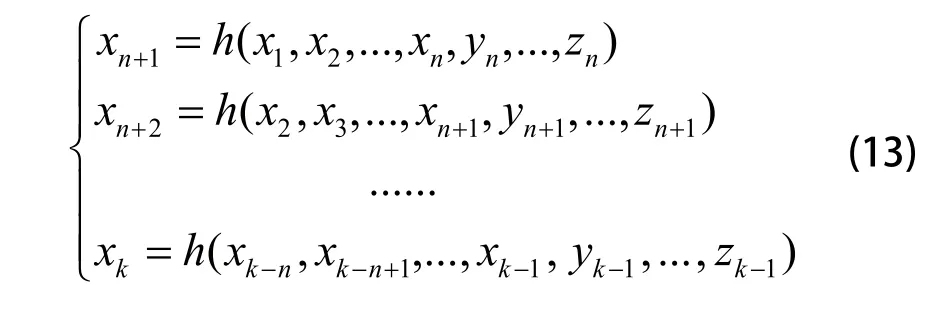
3 仿真实验

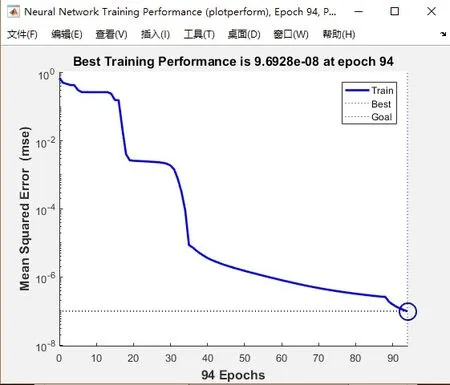
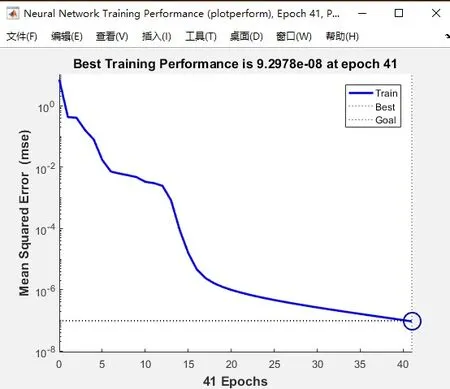



4 结论