基于小波包变换的回转窑托轮轴承故障诊断

艾 红，赵子炜

（北京信息科技大学 自动化学院，北京 100192）

基于小波包变换的回转窑托轮轴承故障诊断

艾 红，赵子炜

（北京信息科技大学 自动化学院，北京 100192）

针对回转窑对象给出了水泥回转窑故障诊断框图。说明了水泥回转窑工艺流程和常见的水泥回转窑设备故障及原因。阐述了小波包分解方法和小波包分解的优缺点。阐述了基于小波包变换的水泥回转窑故障诊断算法，给出了基于小波包变换的轴承故障诊断流程图。对正常状态、外圈故障状态和内圈故障状态的轴承小波包变换进行分析。得到经小波包分解1～4层细节进行重构后的波形图，得到经4层小波包分解后各频带的能量分布以及重构信号的包络图。将正常状态下小波包分解后的能量频谱信号与故障状态下的进行比照，通过能量频谱信号的不同，确定正常状态和故障状态的特征信息。文中对采集到的振动信号进行小波包分解，对分解后不同频带上的信号进行功率谱计算，通过能量的改变表示某一种特征信号，再对提取到的特征信号进行Hilbert谱分析。最终，通过对特征信号的Hilbert谱分析来区分出不同的故障。

回转窑；轴承；小波包变换；故障诊断

0 引言

水泥回转窑在生产过程中可能会发生一些故障，如托轮断轴，齿轮断裂，筒体裂开等故障。回转窑的整体结构较为繁杂，因其具有封闭性的特点，因此无法通过建立数学模型等精确的诊断方法检测故障，大多只能运用人工检测，而人工检测效率低，不能及时有效预防故障，因此给故障诊断带来很大困难。通过对回转窑工艺结构的信号特征进行检测与分析处理，提取其特征信号进行故障诊断，可以有效进行故障预测。本文采用基于小波包变换方法的水泥回转窑轴承故障诊断方法，对振动信号进行小波包分解，挑选出能够表征信号特征的频带进行Hilbert包络谱分析，从包络线中判别轴承的工作状态[1]，为水泥回转窑轴承的不同故障状态提供判别依据。

1 回转窑故障诊断基本流程

水泥回转窑故障诊断的具体实施过程可以归纳为信号采集、信号处理、状态识别和诊断决策四个方面。信号采集是指回转窑在工作时，其内部元件必然会产生振动量的变化，得到一些特征信号，需要使用传感器来收集这些信息。信号处理是将采集到的信号进行加工与处理，以此得到表征回转窑的特征。进行特征分析是用各种信号处理方法，找到工况状态与特征量的关系，把有关故障和无关故障的特征信息分离开，得到真实的故障特征，再经过信号处理滤出混杂的噪声和干扰，将信号变换成容易处理、传输、分析与识别的形式[2,3]。状态识别是将信号处理后得到的特征信号与规定的信号特征进行比较，通过比较确定回转窑的故障类型。诊断决策是根据对回转窑状态的研究，分析整个过程中的诸多信息，对回转窑的现状以及发展趋势做出判断。利用获取的信息进行分析，诊断出故障类型以及故障的具体部位，进而进行提前准备，恢复系统正常运转。图1为水泥回转窑故障诊断的基本流程，表1为回转窑常见故障及其产生的主要原因。

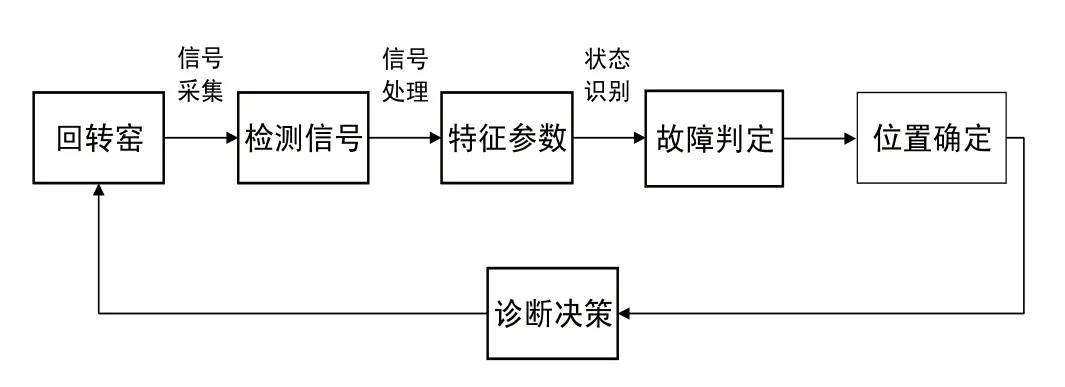
图1 回转窑故障诊断基本流程

表1 回转窑常见故障及其产生的主要原因

2 小波包变换法

基于小波变换的时频域分析方法是指对信号的高频部分具有较低的频率分辨率和较高的时间分辨率，而对于信号的低频部分具有较高的频率分辨率和较低的时间分辨率，即小波变换对信号具有多分辨率分析的特点。

2.1 小波包分解

由于小波变换在高频部分无法细致地进行分解，因此提出小波包分解的方法。小波包分解是对频带进行多层次划分，能够对高频部分进行更加细致的分解，小波包分解的另一个优点就是小波包能够对不同信号进行不同频段的选择，使得分解后的时频分辨率变得更加精确。在回转窑工作过程中，其轴承的振动信号隐含着各种频率成分，当窑轴承发生异常时，轴承的振动信号必然会发生相应变化，这个变化会与正常运行时振动信号产生的能量空间存在相应差异，这个差异正好是反映回转窑轴承发生故障的特征信息。因此，当窑轴承发生故障时，振动信号的部分频率就会发生相应变化，同时与之相对应的频带也会有所增减。所以，对振动信号进行小波包变换，可以通过振动信号的频率特征参数在分解子空间上的能量变化来对窑轴承进行分析。具体做法是将正常状态下小波包分解后的能量频谱信号与故障状态下的进行比照，通过能量频谱信号的不同，确定正常状态和故障状态的特征信息，建立故障信息库，通过实际测量数据小波包分解后的能量频谱分析与故障特征信息对比，来判定实际测量数据表征的轴承是否发生了故障[4,5]。在具体操作中，首先对采集到的振动信号进行小波包分解，然后对分解后不同频带上的信号进行功率谱计算，通过能量的改变来表示某一种特征信号，再对提取到的特征信号进行Hilbert谱分析，从而区分出不同的故障。如果轴承的某一部分出现损伤，在轴承运转过程中遇到损伤点时会发生碰撞而产生持续时间很短的冲击，使构件变形形成自由衰减振动，振动频率取决于系统的固有频率。随着轴承的回转，这种冲击响应以该元件的损伤特征频率重复出现，使振动信号产生了幅值调制现象。采用解调分析方法，可以从高频信号中提取出调制信息，分析其强度和频率可用于判断零件损伤的程度和部位。Hilbert变换包络解调是提取轴承损伤特征频率的有效方法之一，原理是求信号的Hilbert变换对。以信号为实部，Hilbert变换对为虚部，构成解析信号，求解析信号的模，得到采样信号的包络。

2.2 小波包分解的优缺点

小波包分解的优点是具有多分辨分析的特点，在时域和频域上都具有表征信号局部特征的能力，是信号时频分析的优良工具。小波包分解可以对高频部分提供更精细的分解，而且这种分解无冗余，也无疏漏，可以得到比较好的频率局部化。随着分解层数的增加，频带被划分得越来越精细，所以小波包分解是一种比多分辨分析更加细化的分解方法。

小波包分解的缺点是其分解层数的选择如果过大，其分解过程的复杂度就增大，如果分解层数过小，则不能有效地体现出信号的局部信息，不利于特征向量的提取。小波包分解中，最优小波包基函数的选择对信号处理乃至故障诊断有很大关系。要对每个小波包分解系数选择一个适宜的阈值，对其量化，阈值的选择和量化直接关系到信号的消躁质量，通常一次选择并不能取得理想效果，需多次尝试。

3 回转窑故障诊断算法的实现

由于正交小波变换只对信号的低频部分做进一步分解，而对高频部分即信号的细节部分不再继续分解，所以小波变换能够很好地表征一大类以低频信息为主要成分的信号，但它不能很好地分解和表示包含大量细节信息的信号。与之不同的是，小波包变换可以对高频部分提供更精细的分解，而且这种分解既无冗余，也无疏漏，对包含大量中、高频信息的信号能够进行更好的时域局部化分析。根据小波包分析理论可以知道，小波包变换的实质是采用多个互相衔接的等宽带滤波，把信号映射到不同的频带上去，而各个频带可以得到含有不同特征信号的分量，与此同时，信号的能量又能反映出轴承运行的实际状况，而能量高的小波包频带则包含了信号的主要故障特征。因此，对窑轴承的振动信号进行小波包分解，将分解后的信号进行能量求解进而得出各个频带的小波包能量，将能量最大的频带作为振动信号的特征分量来进行Hilbert解调分析，从而得到窑轴承正常运行和故障状态下运行的特征频率。

由于窑轴承振动信号所表现出来的故障信号的复杂性，根据小波包分解理论可以知道，对信号进行小波包分解是对信号提供一种更为精细化的分析方法。小波包分解方法能够对信号在全频带内进行多层次划分，同时又由于小波包分解自身是一种正交分解方法，使得分解得到信号的两个频带互不交叉，同时输出的两个频带带宽减半，因此信息不会因频带的分解而丢失。利用小波包对信号进行分解可以将任意信号分解到相应的频带中去，同时采用每个频带内分解信号的能量来反映轴承的工作状态，再通过相应频带内的能量变化对轴承进行有效地故障分析和诊断[6,7]。

根据小波包分解后某一频带内的能量信号大小作为特征分量进行希尔伯特变换，希尔伯特变换是对非平稳信号进行分析的一个有效分析工具，若有一个实信号可表示为x(t)，则希尔伯特变换的表达式为：

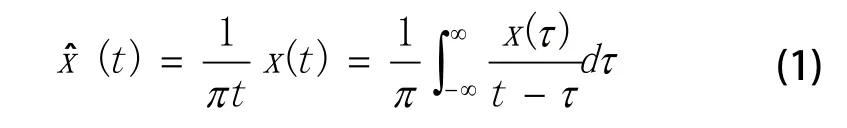
由式(1)可知，对一个确定性信号进行希尔伯特变换过程相当于对该信号进行一次滤波处理。经小波包分解后得到能量最大的频带分量En(t)对该分解信号进行希尔伯特解析信号的包络为：

式中：

En为频带分量；

E'n为En的希尔伯特变换。

利用能量判别方法实现的基于小波包变换方法回转窑故障诊断算法流程如图2所示。在算法实现过程中，首先通过软阈值小波去噪方法去除采集到的振动信号背景噪声，然后进行小波包分解，求得4层小波包频带能量E4,j（j=0，1，…，15），再调用MATLAB软件求最大值函数提取小波包能量最大频带作为待分析的特征分量，对特征分量进行希尔伯特调制分析，从特征分量的Hilbert调制信号中获得调制信号的包络谱，得到损伤特征频率，以此来确定故障具体位置。

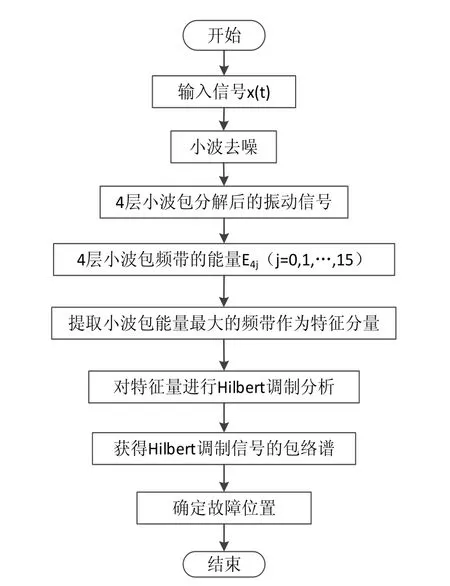
图2 基于小波包变换的轴承故障诊断流程图

4 基于小波包变换的回转窑轴承故障诊断

通过小波包变换的时频分析特性信号可以将振动信号中的冲击成分在小波分解过程中分解，使用小波包变换方法对采集到的振动信号进行变换，同时通过分解小波信号的能量大小寻找故障特征信号，进行希尔伯特变换解调和细化频谱分析，可以有效地将回转窑轴承中的故障信息成分分析出来，找出轴承发生故障的部位。这里选取了3组回转窑轴承振动数据，分别为正常状态下、内圈故障状态下和外圈故障状态下的回转窑轴承振动数据，利用MATLAB软件进行故障分析。在对轴承振动信号的采集过程中，由于外界噪声干扰的存在以及采集系统自身的一些局限性，使得采集到的振动信号与其真实值之间存在一定的偏差，为了更加有效地对采集信号进行分析，要对信号进行预处理[8,9]。

4.1 正常状态的轴承小波包变换分析

图3为正常状态下4层小波包分解后各频带的能量分布情况，可以看出第4层小波分解各频带的能量大小，对能量最大的频带进行Hilbert变换后进行包络分析得到其包络谱情况，如图4所示。

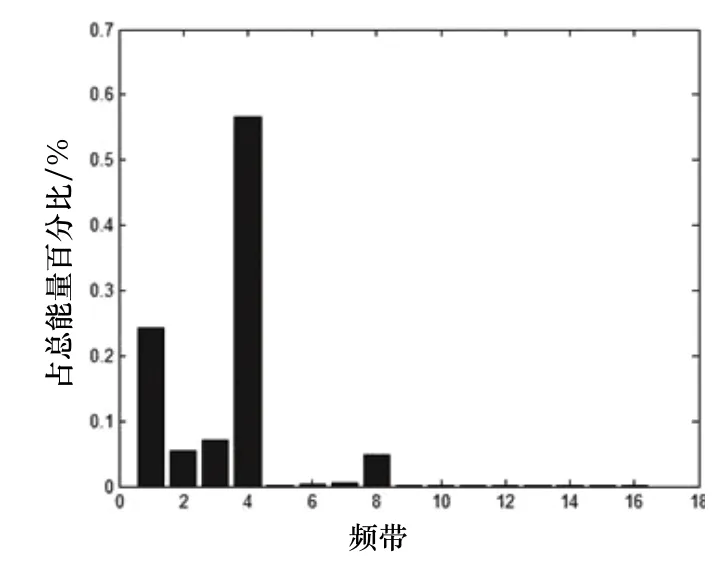
图3 正常状态下分解后各频带的能量分布

图4 正常状态下重构信号的包络谱

由图4可知，正常状态下各频带内的能量分布差异加大。由图5可知，0Hz时功率谱最大，将此频率及功率谱峰值作为判别正常状态的标志来区分不同故障状态。

4.2 外圈故障状态的轴承小波包变换分析

图5为外圈故障状态下4层小波分解后各频带的能量分布情况，可以看出能量最大的频带与正常状态下的分布具有明显的区别，对能量最大的频带进行Hilbert变换后进行包络分析得到其包络谱如图6所示。

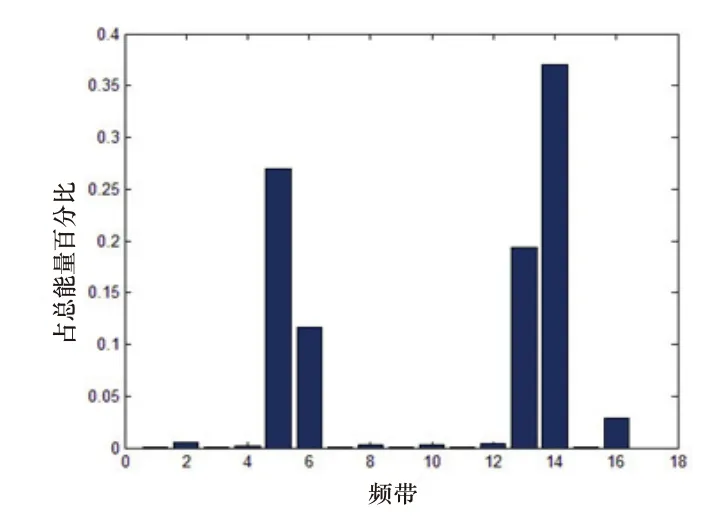
图5 外圈故障下分解后各频带的能量分布

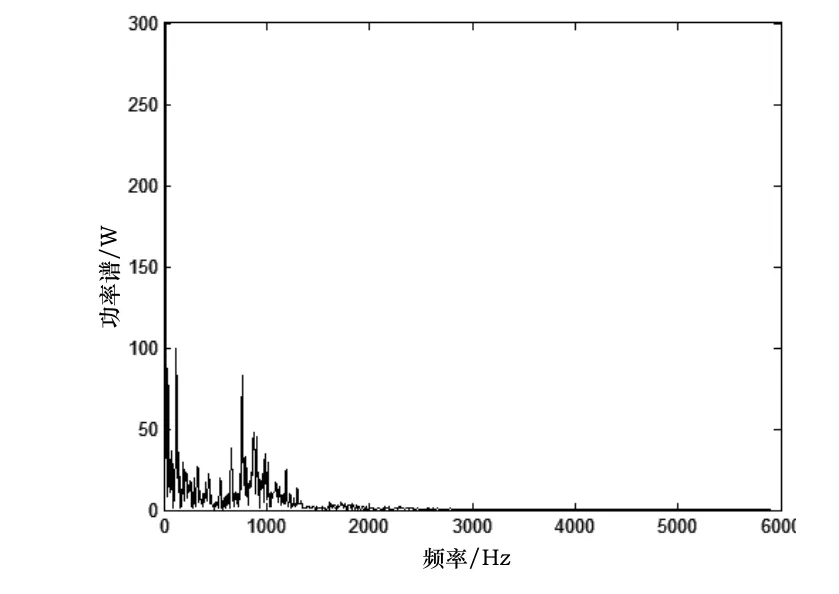
图6 外圈故障下重构信号的包络谱

由图6可知，外圈故障下各频带内的能量分布差异加大，与正常状态下的分布差异明显。由图8可知，功率谱峰值所在的频率较正常状态下变化明显，以此频率及功率谱峰值作为判别外圈故障的标志。

4.3 内圈故障状态的轴承小波包变换分析

图7为内圈故障状态下4层小波包分解后各频带的能量分布情况，可以看出能量最大的频带与正常状态和外圈故障状态下的分布具有明显的区别。对能量最大的频带进行Hilbert变换后进行包络分析得到其包络谱情况，如图8所示，其与正常状态和外圈故障状态的包络图相比有明显区别，且从其功率谱能量中确定是内圈故障。

图7 内圈故障下分解后各频带的能量分布

图8 内圈故障下重构信号的包络谱

由图7可知，内圈故障下各频带内的能量分布差异加大，且与正常状态和外圈故障状态下的分布差异明显。从图8可以看出，功率谱峰值在频率较低和1000Hz处明显，这比正常状态和外圈故障状态下的变化都明显，以此频率及功率谱峰值作为判别内圈故障的标准。

通过3种状态下对滚动轴承的仿真进行分析可以发现，正常状态下的滚动轴承时域波形图与内圈故障和外圈故障状态下的2组时域波形图进行对比时，很难区分正常状态和故障状态。因此，需要对振动信号进行小波包分解。为了更加有效地对正常状态和故障状态进行区分，就需要对分解后的各频带进行能量谱分析，对能量最大的频带进行重构后再进行Hilbert包络分析，通过功率谱峰值出现的位置有效地区分出轴承的正常状态和故障状态。

5 结束语

本文提出了应用小波包变换方法进行回转窑故障诊断的方法，挑选出能够表征信号特征的频带进行Hilbert包络谱分析，从包络线中判别轴承的工作状态。该方法能够有效地提取到故障状态中的特征频率，为水泥回转窑轴承的不同故障状态提供了判别依据。

[1] 张楠,郭丽娟.我国水泥工业发展状况研究[J].赤峰学院学报(自然科学版),2009,25(2):129-131.

[2] 季尚行,张元慈.我国新型干法水泥生产技术的进步和展望[J].水泥工程,2010,(5):3-9.

[3] 柴保明,吴治南,赵志强,等.基于小波包包络分析的滚动轴承故障诊断[J].煤矿机械,2015,(1):283-285.

[4] 王江萍,孙文莉.基于小波包能量谱齿轮振动信号的分析与故障诊断[J].机械传动,2011,35(1):55-58.

[5] 赵锦剑,杨光永,周安然,等.旋转机械振动信号的Kalman滤波及故障诊断[J].仪表技术与传感器,2014,(5):80-83.

[6] Chen Gang,LiuYang,Zhou Wen-an. Research on intelligent fault diagnosis based on time series analysis algorithm[J]. The Journal of China Universities of Posts and Telecommunications,2008,15(1):68-74.

[8] GuoYuyin,JiangBin,ZhangYoumin,ect. Novel robust fault diagnosis method for flight control systems[J].Journal of Systems Engineering and Electronics,2008,19(5):1017-1023.

[9] 周东华,叶银忠.现代故障诊断与容错控制[M].北京:清华大学出版社,2000:24-39.

Fault diagnosis of rotary kiln supporting roller bearing based on wavelet packet transform

AI Hong, ZHAO Zi-wei

TP206.3

：A

1009-0134(2017)07-0010-04

2017-03-27

北京市自然科学基金资助项目（4162025）

艾红（1962 -），女，四川重庆人，教授，硕士，主要从事故障诊断方面的研究。