三轴气浮台重心自动调整研究

潘俊帆 康国华 周琼峰

南京航空航天大学航天学院微小卫星研究中心，南京210000



三轴气浮台重心自动调整研究

潘俊帆 康国华 周琼峰

南京航空航天大学航天学院微小卫星研究中心，南京210000

为了使小型三轴气浮台的重心与旋转中心始终保持一致，分析了三轴气浮台在重力影响下的运动特点，建立了重心到旋转中心的偏移量与三轴上加速度的对应方程，同时引入了弹性形变对平台重心位置的影响，阐述了平台姿态与受弹性形变影响而产生的重心偏移的关系，提出了一种修正弹性形变干扰的气浮台三轴重心调整方法，编写了控制算法，进行了实验验证。 关键词 三轴气浮台；重力；重心调整；弹性形变；物理仿真

在使用三轴气浮台对卫星姿态进行高精度控制时，气浮球轴承的气流摩擦力矩、外界对台体的干扰力矩(如风对台体产生的力矩)、台体的质心与旋转中心不重合而产生的不平衡力矩，以及外界的温度及湿度等因素，都与轨道上存在的干扰不同，因此会影响实验结果。在这些干扰中，质心与旋转中心不重合所产生的不平衡力矩带来的影响最大。因此，能否把质心和旋转中心的重合度控制在适当范围内，对于获得高精度的实验结果至关重要，该项工作通常称为配平。

本文首先建立了三轴气浮台在地面实验时的动力学方程，通过对动力学方程的分析，找出可以作为调整重心与旋转中心差值的参考量。然后对台面受重力影响而产生的弹性形变进行分析，指出了这种形变对重心位置的影响。最后给出了一种全新的三轴气浮台重心调整方法。该方法修正了弹性形变对重心位置的影响，具有调整速度快，适用范围广等特点，适合高精度三轴气浮台使用。

1 气浮台平衡动力学方程

以三轴气浮台的旋转中心为原点，建立当地水平坐标系(OXYZ)和随实验平台一起转动的体坐标系(Oxyz)。当气浮台转动时，其姿态可由3个欧拉角表示。设在初始状态时，实验平台体坐标系与当地水平坐标系完全重合，给定一组目标欧拉角(ψ，θ，φ)，按照3,2,1的顺序转动实验平台，则经过3次旋转后，从当地水平坐标系到目标台体坐标系的变换矩阵C为[1]：

(1)

式中，A=sinψcosφ,B=cosψcosφ,D=sinψsinφ,E=cosψsinφ,φ为偏航角，θ为俯仰角，ψ为滚动角。在小角度情况下，有如下关系[1]：

(2)

式(1)和(2)描述的是气浮台的运动过程，用于建立气浮台的运动学模型。气浮台用于地面实验时，利用平台上的传感器获取位姿信息，利用执行机构模拟对卫星的姿态控制。本文提到的三轴气浮台装有三轴陀螺与倾角传感器，可以获取平台当前的角度与角速度；利用三轴动量轮和十六向喷气装置对平台进行姿态控制。

在地面上利用三轴气浮台进行卫星姿态模拟时，不可避免的会受到重力影响。当实验平台的重心与旋转中心不重合时，重力将在平台上产生静不平衡力矩：

Ts=

(3)

若将平台本身视作刚体，则在运动过程中平台重心与旋转中心的位置都保持不变，其平衡动力学方程可表示为[2]：

(4)

其中，m为转台质量，Ixx为x轴转动惯量，Iyy为y轴转动惯量，Izz为z轴转动惯量，rx，ry，rz分别为旋转中心与重心在x，y，z轴方向相差的量。

由式(3)和(4)可知，当重心与旋转中心不重合时，若气浮台的横滚角和俯仰角不为0，则会产生1个角速度，从而引起姿态的改变。因此，可将平台不处于水平位置时，气浮台姿态在无控状态下是否会自发变化作为判断重心与旋转中心是否重合的依据，同时还可以根据角加速度的大小估计重心位置与旋转中心的差值。

2 弹性形变引起的不平衡力矩分析

上述动力学分析的基础是将三轴气浮台视为刚体，如图1所示。

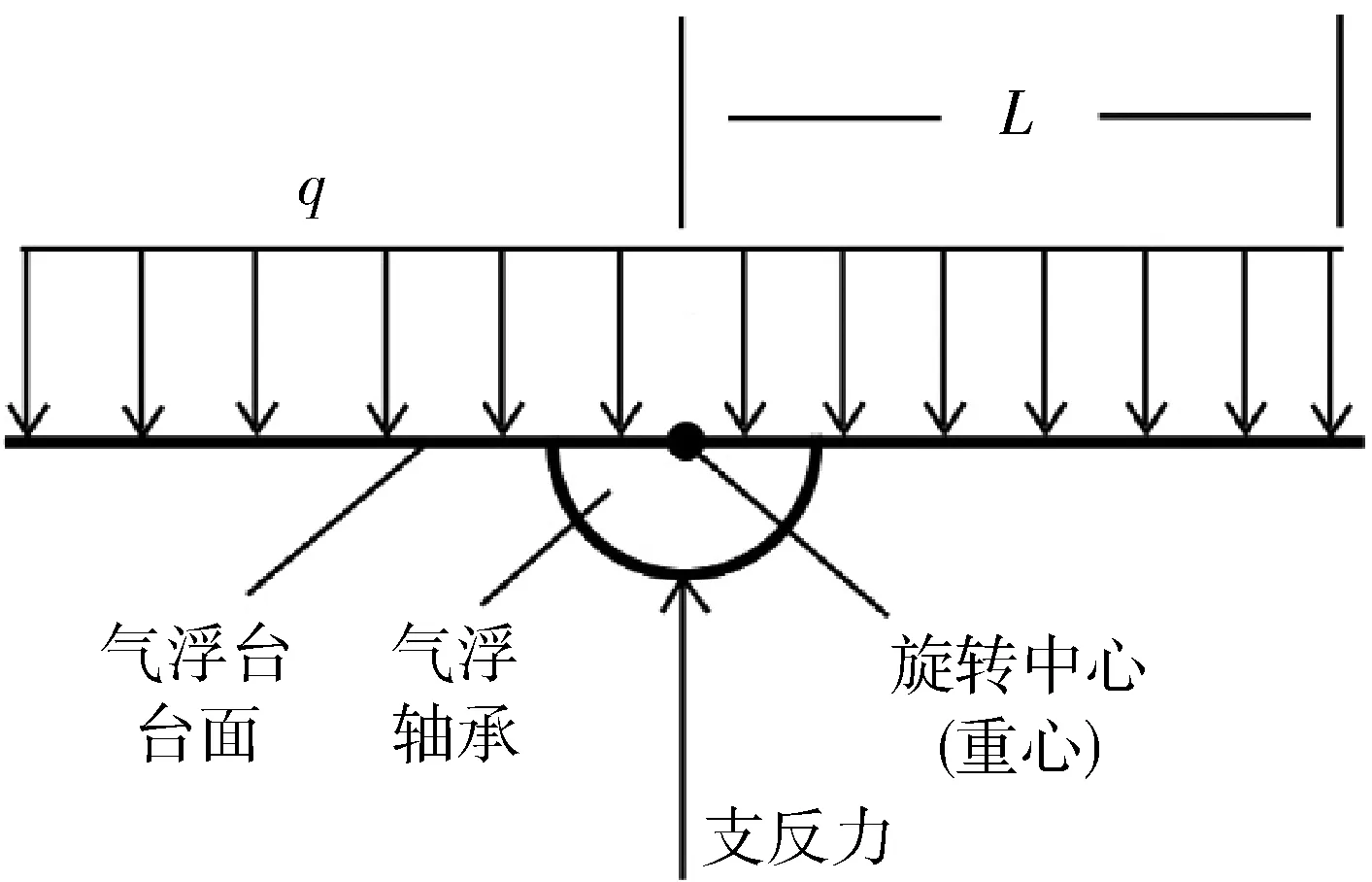
图1 水平刚性平台受力简图

图1中，平台的自重与平台上的载荷可等效为作用于平台表面的均布载荷，平台半径为L。若此时平台已通过配平使旋转中心与重心重合，则整个系统受力情况如图1所示。

若将平台视为弹性体，则在均布载荷q作用下，会在水平位置产生弹性形变。由于弹性形变的影响，此时平台的重心将低于将平台视作刚体时的重心。记平台末端的弹性形变大小为h0，此状态下重心与旋转中心的关系如图2所示。

图2 水平弹性平台受力简图

实验平台固定于气浮球轴承上，并随之转动，故可将实验平台看作中点固支、两端自由的平板。因此,当气浮台上所受载荷为均布载荷时，可用悬臂梁模型对气浮台一侧的受力进行近似分析。其远端的挠度可以通过式(5)和(6)[3]算出：

(5)

(6)

式中，q为沿实验平台径向均布的载荷；L为实验平台的半径；E为平台所用材料的弹性模量；I为截面的惯性矩，与平台的结构设计有关；h0为台面处于水平状态时相对于水平基准线的最大挠度，取竖直向上为正向。式(5)描述的是整个悬臂梁模型的挠度曲线，x为到支点的距离，y为该位置挠度，取竖直向上为正。

图3 倾斜弹性平台受力简图

设实验平台绕X轴转动了一定角度，如图3所示。由于实验平台与水平面产生了一个夹角，因此重力在垂直于台面方向的均布载荷要小于台面处于水平位置时。平台在水平位置时的最大挠度为h0，因此在旋转过程中有h0>h>0。由式(6)可知h的取值与q有关，而q与实验平台转角θ有如下关系：

(7)

因此，平台末端的挠度与实验台的转角对应关系为：

(8)

由式(8)可以看出，台面末端的挠度大小会随台面倾角的变化而变化。若将台面视作均质考虑，可得:

(9)

即整个台面的重心会随倾角的变化而变化。因此，重心应根据台面姿态的变化进行动态调制。

3 三轴气浮台的重心调整方法

三轴气浮台的重心调整一般通过观察气浮台在水平状态下的偏转方向，以添加或移动配重块的方式手动调整。但耗时较长，调整精度较低，同时由于调整时的基准面一般选择在水平面上，当完成重心在XY面上的调整后，无论重心在Z轴上是否有偏差，实验平台都不会发生偏转。因此难以对重心进行Z轴方向上的调整。

现有的自动调平方式也多着眼于重心在XY面内的调整，对Z轴方向的调整多依赖于经验。本文提出的三轴气浮台重心动态调整方法利用了平台上的自动配重模块、台面测量系统以及姿控态统，实现了对实验平台重心的三轴自动调整。整个调整过程如图4所示。具体调整方法如下：

1)首先将进行过粗调平的三轴气浮台置于水平位置，让气浮台处于自由状态，利用实验平台上的传感器测量出此时三轴气浮台绕X，Y轴的角加速度；

2)根据三轴气浮台各轴惯量和飞轮模块飞轮惯量的比值以及测量出的角加速度计算出对应轴向上飞轮的转动加速度，并控制飞轮向三轴气浮台绕X，Y轴转动相同的方向加速转动，通过喷气系统对飞轮进行卸载。此时的控制目标为保持三轴气浮台姿态水平不变；

3)由飞轮维持台面水平所需要的力矩大小以及方向，调节配平滑轨上配重块的位置，使得飞轮维持台面水平所需的力矩逐渐减小，直至飞轮维持常值转速。至此即完成重心在水平面即X，Y轴上的调整；

4)对飞轮进行卸载后，利用X轴(或Y轴)方向的飞轮使实验平台产生倾斜。此时由于重心在Z轴上，尚未完成调整，由于重心位置的不同对台面产生的影响不同。由式(4)可知，若重心在Z轴上高于旋转中心，由重力产生的不平衡力矩会使平台倾斜程度加大，反之则会减小。利用飞轮将平台维持在这一倾斜位置，并根据平台倾斜的趋势移动滑轨上配重块的位置配平，直至平台稳定在这一位置，且飞轮输出常值转速。至此即完成重心在Z轴上的调整。

由于弹性形变的影响，重心在Z轴上的位置会随倾角变化。因此，在倾斜姿态平台完成了Z轴上的重心调整后，此时的调整是和当前姿态对应的。当平台回到水平位置或者进行实验时，Z轴的配重块也需要进行相应的移动来保证重心在目前的姿态下与旋转中心重合。重心和姿态的关系已在式(9)给出，配重的调整量应根据配重与台面质量的比值及重心和姿态的关系决定。

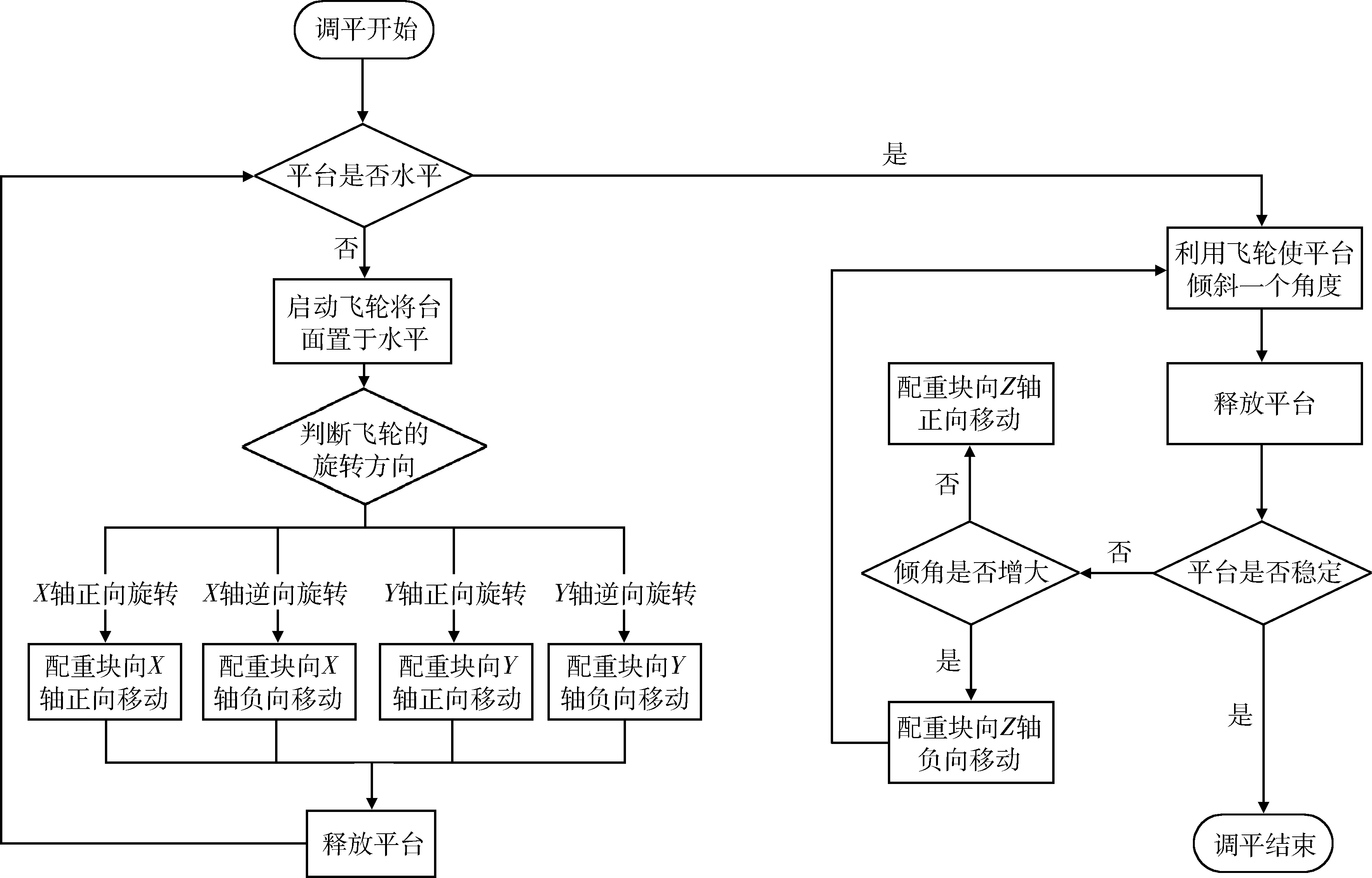
图4 重心自动调整过程流程图

4 调平方法实验验证

4.1 实验设备条件

三轴气浮台的台面直径800mm，台面质量45kg，所加配重块质量1kg，配重块所在滑轨可调节范围为240mm，重心初始时在X，Y，Z三轴上的偏移量分别为4mm，3mm，2mm，台体转动惯量I=(2.41,0,0；0,2.78,0；0,0,3.16)，惯量积为0。

实验台使用动量轮作为执行机构，由喷气系统对动量轮进行卸载。选取对平台不施加控制时的绕X轴和Y轴的角加速度为参考量，根据角加速度的方向和大小确定控制力矩，最终控制目的是使该参考量为0。由实验台数据和式(8)和(9)可得，实验台受弹性形变影响而产生的重心偏移量在10-4量级。

图5 实验平台与三轴调平系统

4.2 实验结果

图6是考虑弹性形变时调整过程中的重心与旋转中心的差的变化。图7是对应的调整过程中实验台台面的姿态变化。如图所示，重心调整由XY面开始，再到Z轴。调整的过程中，台面的姿态会产生的一定的起伏，这种姿态的波动会随重心与旋转中心的接近而逐渐减小。在10°附近完成此姿态下的重心调平后，由于考虑到弹性形变在不同姿态下对重心有不同的影响，重心的调整还将随台面姿态的变化而变化。因此当平台姿态回到水平后，重心与旋转中心依然重合。图8是未考虑弹性形变时调整过程中的重心与旋转中心的差的变化。图9是对应的调整过程中实验台台面的姿态变化。整个调整过程中平台姿态的变化与考虑弹性形变的调平方式类似。如图所示，尽管10°时重心与旋转中心调整到了重合的位置，但是随着实验平台回到水平，重心与旋转中心的差值又逐渐增大。

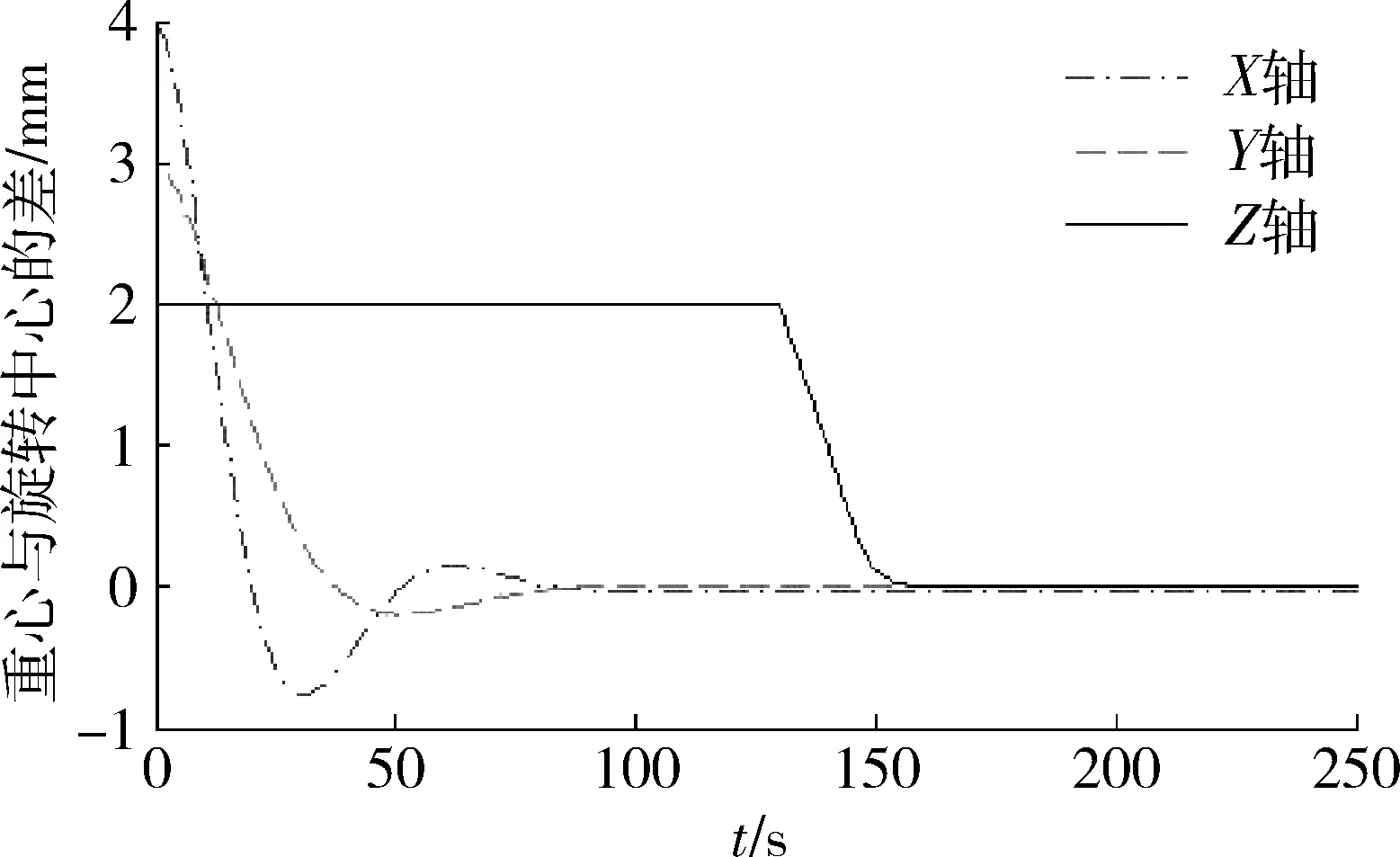
图6 考虑弹性形变时调整过程中的重心与旋转中心的差的变化

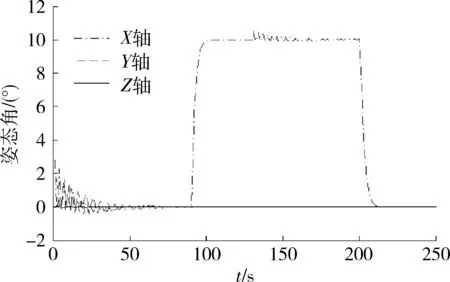
图7 考虑弹性形变时调整过程中的实验台姿态变化

图8 不考虑弹性形变时调整过程中的重心与旋转中心的差的变化

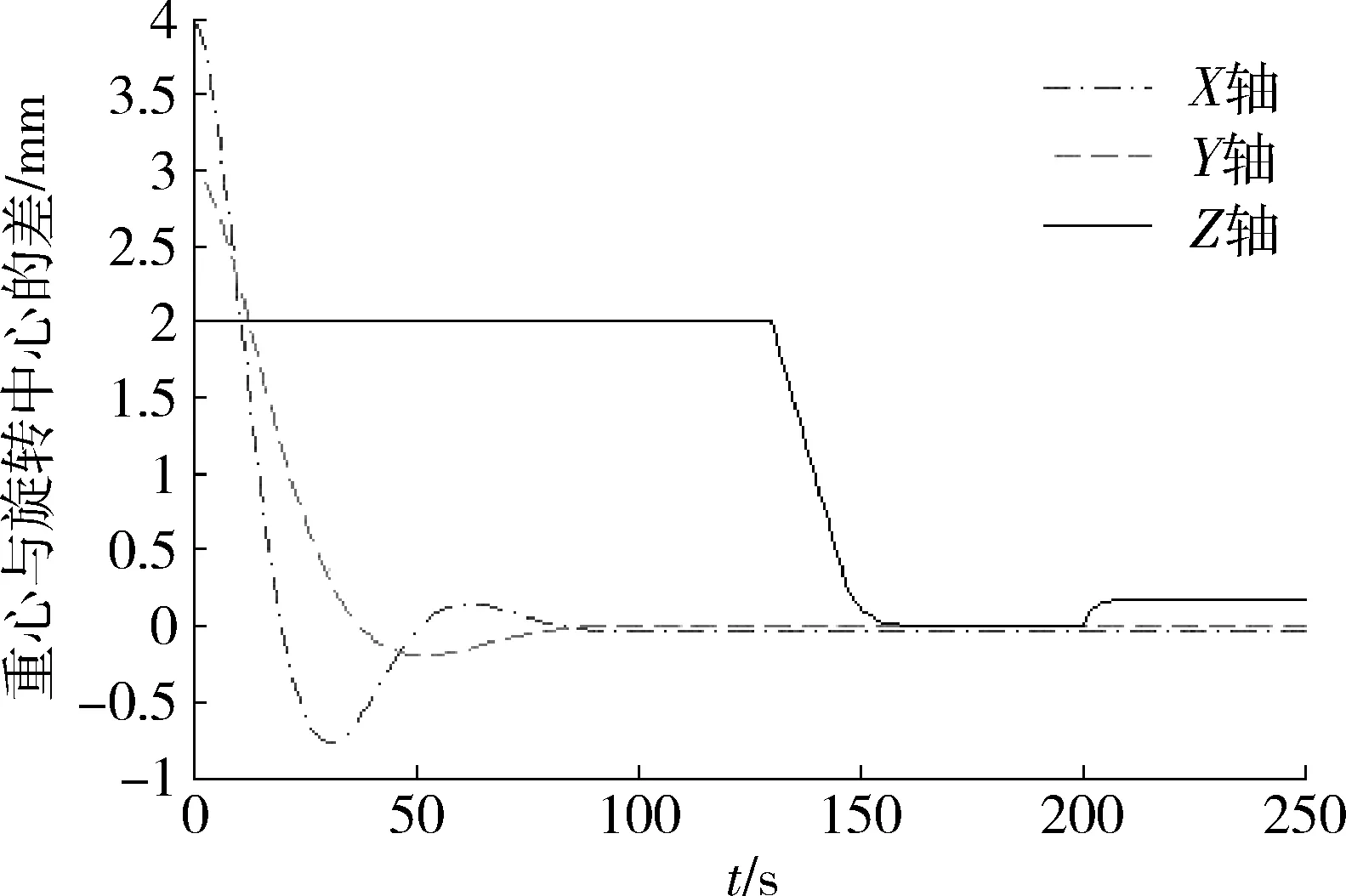
图9 不考虑弹性形变时调整过程中的实验台姿态变化

由以上实验结果可以看出，该调平方法突破了以往重心调整仅在X，Y面内的限制。对重心在Z轴上的偏移也有很好的调整效果。由于本方法同时考虑了弹性形变对台面重心造成的影响，将重心的调整与姿态的变化联系起来，因此使得平台在任何位置都能保持重心与旋转中心的重合，从而在最大程度上减少了由重力带来的干扰力矩。应用本方法的整个调平过程平稳而快速，为后续的实验打下了良好的基础。

5 结论

分析了三轴气浮台的重心调整影响因素，提出了一种适用于三轴的重心调整方法，并通过实验验证，得到如下结论：

1)通过对重力导致的台面弹性形变与调平配置的影响分析，得出了弹性形变造成的重心偏移与姿态之间的关系，提出了一种可以主动消除该干扰的调平方法；

2)通过调平实验，深入分析了弹性形变以及姿态改变对气浮平台重心位置的影响，由此设计了一种自动调平方法，通过仿真验证了该方法能在较短的时间内自动完成气浮台重心在三轴上的位置调整。

该调平方法还可用于模拟重心与旋转中心始终保持一定距离的情况(如重力梯度力矩对卫星的影响)，对于增加地面的仿真能力，提高仿真实验精度有着重要意义。

[1] 杨秀彬，金光，徐开. 三轴气浮台自动调节平衡和干扰力矩测试[J]. 空间科学学报，2009,29(1):34-38.(YangXiubin,JinGuang,XuKai.AdjusttotheBalanceofThree-DOFAir-bearingPlatformandtheTestsofDisturberTorque[J].Chin.J.Space.Sci,2009,29(1):34-38.)

[2] 李延斌，向东，高有华. 重力引起的三自由度气浮台各类不平衡力矩关系及影响[J]. 机械工程学报，2015,51(21):7-14.(LiYanbin,XiangDong,GaoYouhua.RelationandInfluenceofAllKindsofUnbalanceTorquesofThreeDegreesofFreedomAir-bearingPlatformCausebyGravity[J].JournalofMechanicalEngineering, 2015,51(21):7-14.)

[3] 单祖辉. 材料力学[M]. 北京：高等教育出版社，2010.(ShanZuhui.StrengthofMaterials[M].Beijing:HigherEducationPress,2010.)

[4] 邱万彬，陆婷婷. 基于计算机视觉的三轴气浮台姿态确定[J]. 计算机测量与控制，2015，23(2):554-557.(QiuWanbin,LuTingting,AttitudeDeterminationof3-axisAirBearingTableBasedontheComputerVision[J].ComputerMeasurement&Control, 2015,23(2):554-557. )

[5] 田留德，赵建科，薛勋,等. 基于单轴气浮台的角动量输出测量方法[J]. 中国测试，2011，37(6):41-44.(TianLiude,ZhaoJianke,XueXun,etal.MeasurementMethodofAngularMomentumOutputBasedonOne-axisAirBearingTest-bed[J].ChinaMeasurement&Test, 2011,37(6):41-44 .)

[6] 张振军，董云峰. 利用动量轮测试气浮台干扰力矩的新方法[J]. 计算机测量与控制，2008,16(8):1122-1124.(ZhangZhenjun，DongYunfeng.NewMethodforTestingInterferenceTorqueofAirBearingPlatformbyMomentumWheel[J].ComputerMeasurement&Control, 2008,16(8):1122-1124.)

[7] 刘超，何平，李岐,等. 基于三轴气浮台的卫星姿态控制系统物理仿真[J]. 哈尔滨商业大学学报，2015,31(1):65-68.(LiuChao,HePing,LiQi,etal.PhysicalSimulationofSatelliteAttitudeControlSystemBasedonThree-axisAirBearingplatform[J].JournalofHarbinUniversityofCommerce, 2015,31(1):65-68.)

[8]Reynerson，CharlesM.AerodynamicDisturbanceForceandTorqueforSpacecraftandSimpleShapesUsingFinitePlateElements-PartII：Aerodynamicforce&torque[C]// 2012IEEEAerospaceConference，March3-10，2012，BigSky，MT，UnitedStates，2012：1-9.

[9]BaeJ，KimY.AdaptiveControllerDesignforSpacecraftFormationFlyingUsingSlidingModeControllerandNeuralNetworks[J].JournaloftheFranklinInstitute，2012,349(5)：578-603.

[10]VerbinD,LappasVJ.RapidRotationalManeuveringofRigidSatelliteswithHybridActuatorsConfiguration[J].JournalofGuidanceControlandDynamics, 2013,36(2): 532-547.

[11]LongbothamN,BleilerC,ChaapelC,etal.SpectralClassificationofWorldview-2Multi-AngleSequence[C] //IEEEGRSSandISPRSJointUrbanRemoteSensingEvent.Munich,Germany:IEEEComputerSociety, 2011: 109-112.

[12]BoyarkoGA,RomanoM,YakimenkoOA.Time-OptimalReorientationofaSpacecraftUsinganInverseDynamicsOptimizationMethod[J].JournalofGuidanceControlandDynamics, 2011,34(4): 1197-1208.

[13]BassetG,XuY,YakimenkoOA.ComputingShort-TimeAircraftManeuversUsingDirectMethods[J].JournalofComputerandSystemsSciencesInternational, 2010,49(3): 481-513.

[14]VerbinD,LappasVJ,Ben-AsherJZ.Time-EfficientAngularSteeringLawsforRigidSatellites[J].JournalofGuidanceControlandDynamics, 2011,34(3):878-892.

[15]VerbinD,LappasVJ.RapidRotationalManeuveringofRigidSatelliteswithHybridActuatorsConfiguration[J].JournalofGuidanceControlandDynamics, 2013,36(2):532-547.

Research on the Automatic Adjustment of Center of Gravity on Three-Axis Air-Bearing Platform

Pan Junfan，Kang Guohua，Zhou Qiongfeng

Nanjing University of Aeronautics and Astronautics, Nanjing 210000, China

Inordertomakethecenterofgravityofthethree-axisairbearingtableconsistentwiththerotationcenter,themotioncharacteristicsofthreeaxisairbearingtableareanalyzedundertheinfluenceofgravityinthispaper.Theequationofaccelerationisestablishedonthethree-axiscorrespondingtotheoffsetofthecenterofgravitytothecenterofrotation.Inviewofelasticdeformation,theequationofplatformattitudeandthecenterofgravityshiftarealsobuiltduetoelasticdeformation.Inthispaper,acenterofgravityadjustmentmethodofthreeaxisofairbearingtablewithmodifiedelasticdeformationinterferenceispresented.Thecontrolalgorithmofthiscenterofgravityadjustmentmethodisdevelopedandthisalgorithmisproventhatitiseffectivethroughthephysicalsimulationofthree-axisairbearingtable.

Three-axisair-bearingplatform;Gravity;Centerofgravityadjustment;Elasticdeformation;Physicalsimulation

2016-08-02

潘俊帆(1992-)，男，吉林人，硕士研究生，主要研究方向为卫星总体设计与姿控；康国华(1978-)，男，福建人，教授，硕士生导师，主要研究方向为卫星总体设计与姿控；周琼峰(1993-)，女，浙江人，硕士研究生，主要研究方向为卫星总体设计与姿控。

V416.2

A

1006-3242(2017)02-0083-06