J2摄动下卫星相对运动解析方程研究*

周 敬 郑建华 李明涛

1.中国科学院国家空间科学中心, 北京 100190 2.中国科学院大学，北京100190



J2摄动下卫星相对运动解析方程研究*

周 敬1,2郑建华1,2李明涛1,2

1.中国科学院国家空间科学中心, 北京 100190 2.中国科学院大学，北京100190

在圆/近圆参考轨道下，依据含有J2摄动的卫星相对运动动力学模型，提出将变化幅度较小的地心距及轨道倾角平均化，求解J2摄动下卫星相对运动动力学模型，获得了适用于任意初始条件的、以相对位置和相对速度为变量的、解析形式的J2摄动卫星相对运动方程。仿真结果表明，与经典CW方程相比，J2摄动下卫星相对运动精度提升明显，证明了所提方法的合理性和准确性。 关键词 相对运动；CW方程；J2摄动；解析方程

卫星间的相对运动是国际航天动力学与控制领域的研究热点之一，同时也是卫星编队飞行、交会对接和空间攻防等任务的动力学基础。因此，研究卫星间的相对运动具有重要意义。

目前国内外研究卫星相对运动主要采用2种方法：1)基于相对位置和相对速度描述的动力学法[1-3]；2)基于相对轨道根数或其变化形式描述的运动学法[4]。在动力学方法中最简单、最基本的就是CW方程，但其前提假设是理想球体、圆参考轨道和卫星间相对距离足够近，限制了其进一步应用。J2摄动是近地航天器最主要的摄动力，因此研究高精度卫星相对运动首先要考虑的就是J2摄动。目前关于J2摄动下卫星相对运动的研究多采用运动学方法，如参考文献[5-12]，也有参考文献[13]提出可以直接采用数值积分的方法分析J2摄动下的卫星相对运动，虽然此方法计算精度较高，但在理论分析方面效果稍差，计算复杂，不利于星上自主导航或地面的实时处理。理论上，J2摄动下的卫星相对运动动力学模型是一个超越方程，无法通过常规方法获得解析解。为获得解析解，张锦绣[6]以初始时刻主从星的平均轨道根数偏差为变量，在一阶长期意义下，忽略主从星轨道根数中的短周期项，推导出J2摄动下卫星相对运动的精确解析模型。参考文献[14-16]通过研究特定的相对运动初始条件，同样获得了解析形式的相对运动方程，虽具有一定的局限性，但仍具有启示意义。

目前国内外关于J2摄动下相对运动方程的研究绝大部分是以轨道根数描述的，此种描述形式虽然精度较高，但非常复杂。也有其他研究方法，参考文献[17]将J2摄动引起的误差表达式添加到CW方程解析解上，得到了J2摄动下的相对运动表达式；参考文献[18-19]利用拉格朗日方程，推导了高精度的J2摄动下相对运动动力学方程。此外，现有的研究成果多数也是以卫星编队飞行作为研究背景，这就意味着存在航天器等周期这样的隐含约束条件，但某些航天任务，如交会对接、相对轨道转移和空间飞越观测等都不满足这样的约束条件。基于此，研究J2摄动下，以相对位置和相对速度为变量的、形式简单的、无隐含约束条件的相对运动解析方程具有重要研究价值。

本文通过研究J2摄动下的相对运动动力学模型式(3)发现，如果参考卫星的地心距和轨道倾角为常量，则模型可解。通过STK(Satellite Tool Kit)仿真验证，J2摄动下卫星的地心距和轨道倾角恰好变化幅度较小，可近似为常量。因此提出将地心距和轨道倾角平均化，并作为常量代入到J2摄动相对运动动力学模型中。基于此，J2摄动相对运动动力学模型便由不可解的超越方程变为可解的常微分方程，通过求解得到J2摄动下的相对运动近似解析方程。

1 J2摄动下卫星相对运动动力学模型

卫星间的相对运动描述源自20世纪60年代Clohessy和Wiltshire[20]提出的CW方程。该方程建立在圆/近圆参考轨道、无摄动且卫星之间相对距离较近三点假设之上，可在短时间内对卫星间相对运动进行较高精度的描述。然而，随着时间积累其误差逐渐增大。为解决此问题，国内外学者做了很多研究工作以改进CW方程。此外，为满足椭圆参考轨道卫星相对运动研究的需要，Lawden和Carter等以真近点角或偏近点角为独立变量，提出了可适用于任意Kepler轨道的、不考虑摄动情况的相对运动解析解[21]。

一般情况下，相对运动模型建立在相对运动坐标系下，相对运动坐标系也称为RIC坐标系(Radial—In-Track—Cross-Track)，该坐标系以参考卫星质心为坐标原点，以参考卫星的轨道平面作为基本平面，X轴沿参考卫星径向方向，Z轴沿参考卫星轨道平面法向方向，Y轴满足右手坐标系。卫星间的相对运动及相对运动坐标系见图1。

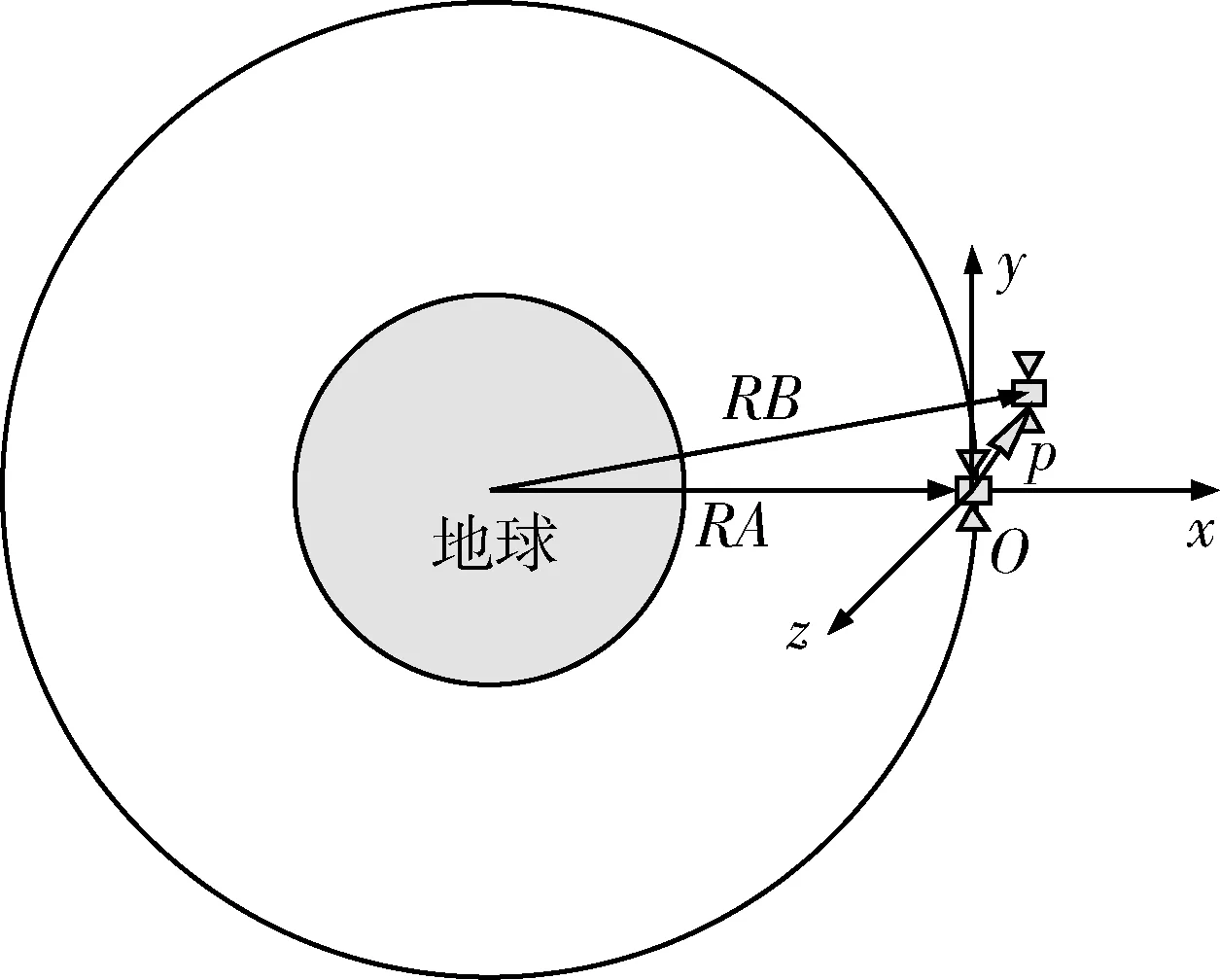
图1 卫星相对运动及相对运动坐标系

无摄动力下的卫星相对运动动力学方程为：

(1)

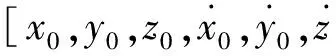
(2)

此即为经典的CW方程。SamuelA.Schweighart从上述经典的CW方程出发，考虑地球J2摄动的影响，将J2项摄动加速度添加到相对运动动力学模型里，改进了圆/近圆参考轨道的相对运动动力学方程[22]。在相对运动坐标系下，改进的相对运动动力学方程为：

(3)

其中，各项参数关系如式(4)所示, 更多参数设置可以参考文献[23]。

(4)

2 J2摄动下卫星相对运动动力学模型求解

Yeh[16]通过研究发现，在改进的动力学模型式(3)下，当初始条件满足一定关系时可以得到相应的解析解，具体内容可查看参考文献[16]。虽然该文献中的卫星相对运动模型可以提供解析形式的运动方程，但是需要研究特定的初始条件，即特定的初始相对位置和相对速度之间的关系，因此不具有普适性。

理论上，J2摄动下的相对运动动力学模型式(3)为超越方程，无法通过常规方法获得其解析解。研究式(3)发现，如果参考卫星的地心距和轨道倾角为常量，则模型可解。而J2摄动下卫星的地心距和轨道倾角虽然会出现长期项、长周期项和短周期项等变化项，但变化幅度很小，恰好可以近似为常量。以太阳同步轨道为例，卫星地心距和轨道倾角变化趋势如图2和3所示，具体变化值见表1。

表1 J2摄动下圆轨道地心距与轨道倾角变化情况

图2 J2摄动下地心距变化情况

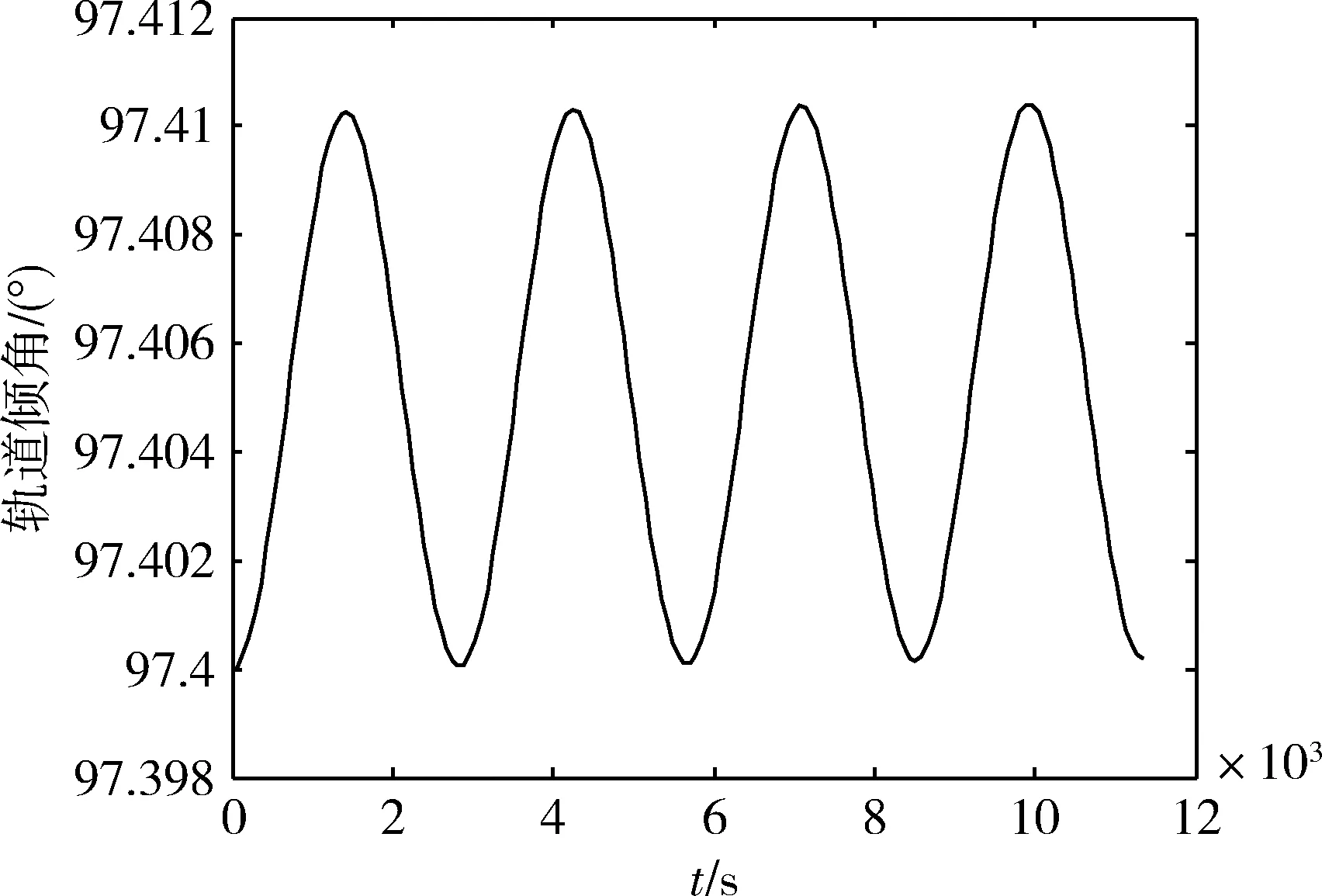
图3 J2摄动下轨道倾角变化情况

根据表1，为得到J2摄动下相对运动解析形式，可以合理假设变化幅度很小的卫星地心距、轨道倾角为常量，具体值可以取为平均轨道根数：

(5)

根据式(3)可以看出，Z轴相对运动与其他两轴相对运动是解耦的，因此可以分别研究Z轴相对运动和XY平面相对运动。一般情况下，相对运动在Z轴的分量较小，Z轴相对运动的精度对综合精度影响很小。此外，在相对运动动力学模型中，Z轴的系数l,q,φ是2颗卫星升交点赤经及其变化率的函数，如式(6)所示，虽然相关文献[12]给出了相应

的计算公式，但是需要求解平均轨道根数，这偏离了本文避免使用轨道根数的初衷。因此，本文不再简化Z轴相对运动，而是直接采用CW方程中的Z轴相对运动形式：

z(t)=c′sin(nt+φ)

(6)

其中，

(7)

综上，J2摄动下XY平面内的相对运动动力学模型可以通过数学处理转化为：

(8)

其中，

(9)

由此，J2摄动下的相对运动动力学模型便可由不可解的超越方程式(3)转化为可解的常微分方程式(8)，求解常微分方程式(8)，可得三轴相对运动方程为：

(10)

由于该解析解消除了特定的初始条件限制，可以适用于任意初始条件，因此具有普适性。

3 数值仿真及结果分析

为验证所提方法的合理性和准确性，本文采用与STK仿真数据、CW方程数据对比验证的方法。

假设初始时刻2颗卫星形成非等周期相对运动，其轨道根数、轨道根数之差转化到相对运动坐标系下的位置偏差与速度偏差如表2所示。

表3表示以STK数据为基准，在相同的初始条件下，CW方程仿真数据和J2摄动下解析运动方程仿真数据的精度比较结果。为使仿真结果更具有针对性、统一性和科学性，在STK仿真模型中仅考虑J2摄动，没有考虑大气阻力、日月引力等其他摄动。

表2 初始时刻两卫星轨道根数与相应的位置、速度误差

表3 CW方程与J2摄动解析方程精度对比(2轨)

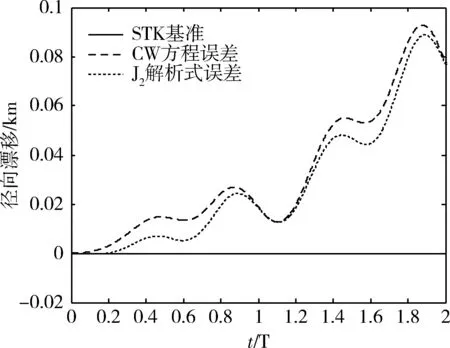
图4 径向相对运动误差

图5 迹向相对运动误差

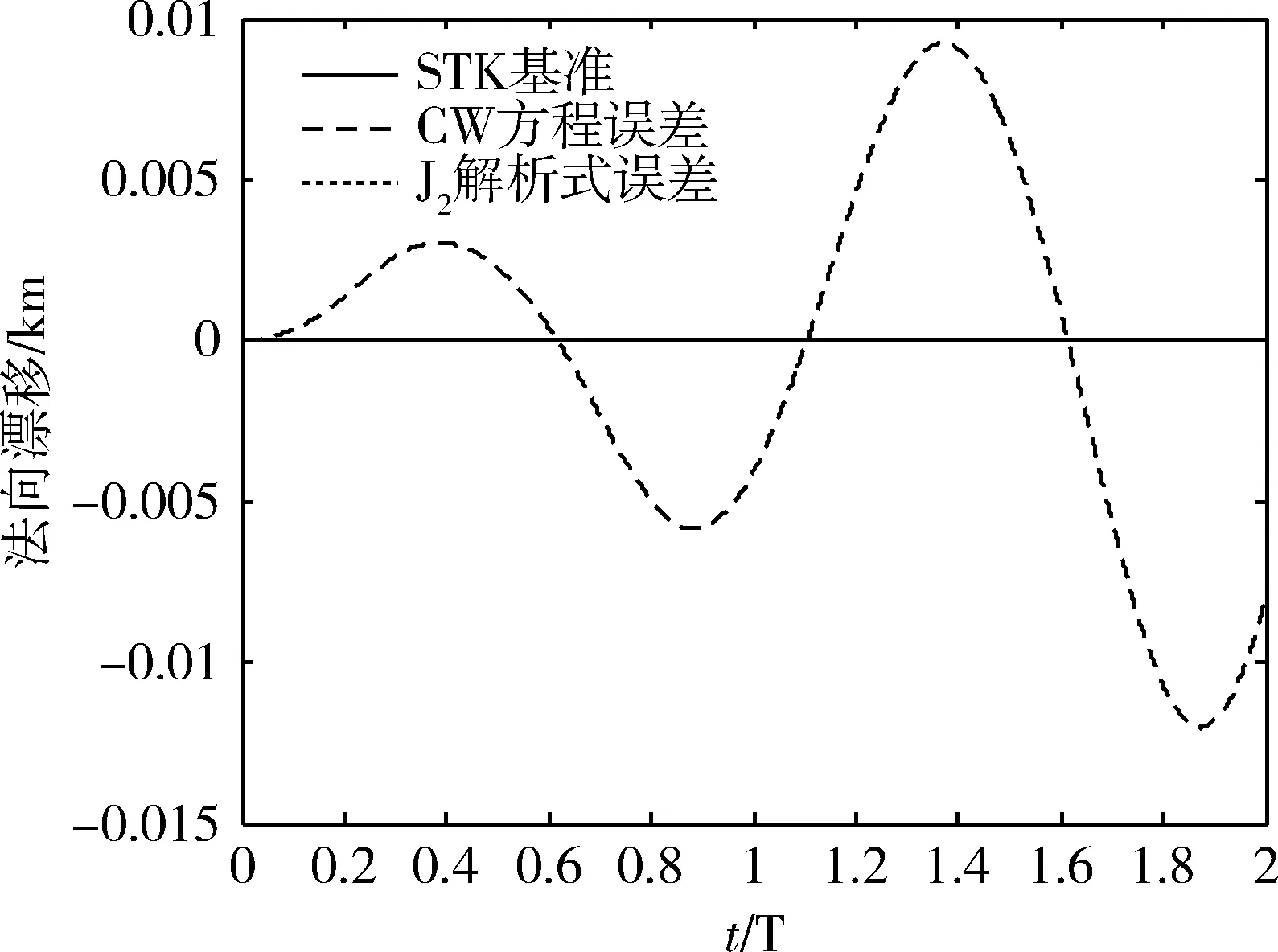
图6 法向相对运动误差

图7 综合相对运动误差

图4～7为2颗卫星相对运动在2轨道周期内，以STK仿真数据为基准， CW方程仿真数据和J2摄动解析运动方程仿真数据在径向、迹向和法向三轴分量以及综合情况下的相对运动绝对误差变化曲线。在径向方向上，J2摄动解析方程相比CW方程精度有提升，但提升幅度较小，见图4；在迹向方向上，J2摄动解析方程相比CW方程精度明显提升，见图5；在法向方向上，J2摄动解析方程相比CW方程精度相同，见图6。

表3提供了相对运动精度提升的具体数值信息。可以看出，以STK仿真数据为基准，2轨道周期内，CW方程在终点时刻的误差是150m量级，平均误差是80m量级，而J2摄动解析方程在终点时刻的误差是80m量级，平均误差是40m量级，精度提高约2倍；尤其在迹向方向，CW方程在终点时刻的误差是130m量级，平均误差是70m量级，而J2摄动解析方程在终点时刻的误差是12m量级，平均误差是20m量级，终点时刻精度提高约10倍，平均精度提高约4倍。

综上，本文所推导的J2摄动卫星相对运动解析方程相对CW方程精度更高，更具优势。

4 结论

J2摄动作用下，卫星相对运动动力学模型为超越方程，通过常规方法无法获得类似CW方程解析形式的相对运动方程。但对于圆/近圆参考轨道，由于J2摄动下地心距及轨道倾角变化很小，可以合理假设为不变量，卫星相对运动动力学方程便由不可解的超越方程转化为可解的常微分方程。仿真结果表明，在考虑J2摄动下，本文所提方法相比CW方程，相对运动精度提升明显，尤其在迹向方向，相对运动精度可以提高约4倍。因此本文推导的J2摄动相对运动解析方程具有一定的实际工程应用价值，可以应用于航天器交会对接、卫星编队飞行等领域。

[1] Karlgaard C D, Lutze F H. Second_order Relative Motion Equation [J]. Journal of Guidance, Control, and Dynamics,2003,27(1):499-501.

[2] Vaddi S S, Vadali S R, Alfriend K T. Formation Flying：Accomdating Nonlinearity and Eccentricity Perturbations[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(2):214-223.

[3] Sedwick R J, Miller D W, Kong E M C. Mitigation of Differential Perturbations in Clusters of Formation Flying Satellites[R]. AAS/AIAA Space Flight Mechanics Meeting, American Astronautical Society, AAS Paper, Feb,1999, 99-124.

[4] 李俊峰, 雪丹. 编队卫星相对运动描述方法综述[J]. 宇航学报, 2008, 29(6): 1689-1694.(Li Junfeng, Xue Dan. Review of Relative Motion Description Methods for Satellite Formation Flying [J]. Journal of Astronautics, 2008, 29(6): 1689-1694.)

[5] Sabol Chris, Burns Richard, McLaughlin Craig A. Satellite Formation Flying Design and Evolution [J]. Journal of Spacecraft and Rockets,2001,38 (2):270-278.

[6] Schaub H, Vadali S R, Junkins J L, et al. Spacecraft Formation Flying Control Using Mean Orbit Elements[J]. The Journal of Astronautical Sciences, 2000, 48(1):69-87.

[7] Alfriend K T, Schaub H. Dynamics and Control of Spacecraft Formations Challenges and Some Solutions[J]. Journal of the Astronautical Sciences, 2000, 48(2):249-267.

[8] 潘立公, 冯祖仁, 刘建平, 等. J2摄动影响下椭圆参考轨道的相对运动模型研究[J]. 系统仿真学报, 2011, 23(4): 648-651.(Pan Ligong, Feng Zuren, Liu Jianping. Study on Relative Motion Model of Elliptical Reference Orbit Under Influence of J2Perturbation [J].Journal of System Simulation, 2011, 23(4): 648-651.)

[9] 张锦绣, 曹喜滨, 王继河. J2摄动情况下编队飞行卫星相对运动精确解析模型研究[J]. 应用基础与工程科学学报, 2007, 15(3): 342-350.( Zhang Jinxiu, Cao Xibin, Wang Jihe. Precision Analytical Equation to Relative Motion of Formation Flying Satellites for J2Perturbation [J]. Journal of Basic Science and Engineering, 2007, 15(3): 342-350.)

[10] Dong-Woo Gim, Kyle T Alfriend. Satellite Relative Motion Using Differential Equinoctial Elements [J]. Celestial Mechanics and Dynamical Astronomy, 2005, 92 (3):295-336.

[11] Schaub H. Relative Orbit Geometry Through Classical Orbit Element Differences [J]. Journal of Guidance Control and Dynamics, 2004, 27(5):839-848.

[12] Alfriend K T, Echaub H, Gim D W. Gravitational Perturbations, Nonlinearity and Circular Orbit Assumption Effects on Formation Flying Control Strategies [C]. The Richard H. Battin Astrodynamics Conference, College Station, TX,USA, March, 2000.

[13] 黄勇, 李小将, 王志恒, 等. J2项和大气阻力摄动作用下卫星编队构型的演化分析[J]. 航天控制, 2013, 31(3): 62-66.(Huang Yong, Li Xiaojiang, Wang Zhiheng. The Evolvement Analysis of Satellite Formation under J2Term and Atmosphere Drag Perturbation[J]. Aerospace Control, 2013, 31(3): 62-66.)

[14] 孟云鹤, 戴金海. J2摄动影响下的卫星编队稳定性分析, 仿真与构形设计[J]. 系统仿真学报, 2005, 17(2): 483-487.(Meng Yunhe, Dai Jinhai. Analysis of Stability、Simulation and Configuration Design for Satellite Formation under the Influence of the J2Perturbation[J]. Journal of System Simulation, 2005, 17(2): 483-487.)

[15] Schweighart S, Sedwick R. A Perturbative Analysis of Geopotential Disturbances for Satellite Cluster Formation Flying[C]//Aerospace Conference, 2001, IEEE Proceedings. IEEE, 2001, 2: 2/1001-2/1019 vol. 2.

[16] Yeh H H, Sparks A. Geometry and Control of Satellite Formations[C]//American Control Conference, 2000. Proceedings of the 2000. IEEE, 2000, 1(6): 384-388.

[17] 马艳红. CW 制导误差分析[J]. 航天控制, 2009, 27(5): 38-42.(Ma Yanhong.The Error Analysis of C-W Guidance[J].Aerospace Control, 2009, 27(5): 38-42.)

[18] 徐光延, 项峰, 谌颖. 高阶带谐摄动下卫星相对运动精确动力学模型[J]. 宇航学报, 2012, 33(9): 1203-1209.(Xu Guangyan, Xiang Feng, Chen Ying. Exact Dynamics Model of Satellite Relative Motion under Arbitrary Zonal Harmonic Perturbations[J]. Journal of Astronautics,2012, 33(9): 1203-1209.)

[19] 杏建军, 时伟, 蒋炳炎. J2项摄动条件下线性化的编队卫星动力学方程[J]. 宇航学报, 2013, 34(5):605-610.(Xing Jianjun, Shi Wei, Jiang Bingyan. Linearized Formation Flight Dynamics Model under J2Perturbation [J]. Journal of Astronautics,2013, 34(5):605-610.

[20] Clohessy W H, Wiltshire R S. Terminal Guidance System for Satellite Rendezvous[J]. Journal of the Aerospace Science, 1960,27(5):653-658,674.

[21] 曹喜滨. 航天器编队动力学与控制[M]. 国防工业出版社, 2013.

[22] Schweighart S A, Sedwick R J. High-Fidelity Linearized J Model for Satellite Formation Flight[J]. Journal of Guidance, Control and Dynamics, 2002, 25(6): 1073-1080.

[23] 孟云鹤. 航天器编队飞行导论[M]. 国防工业出版社, 2014.

Analytical Solutions for Satellite Relative Motion under J2Perturbation

Zhou Jing1,2， Zheng Jianhua1,2， Li Mingtao1,2

1. National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China 2. University of Chinese Academy of Sciences, Beijing 100190, China

Satellite’sorbitalelementscancontainsecularandperiodiccomponentsundertheJ2perturbationwhichresultsinthattherelativemotiondynamicsmodelbecometranscendentalequationsandtheanalyticalsolutionscannotbeobtainedthroughconventionalmethods.Underthiscircumstances,thedistancecanbeaveragedamongthesatellite,theearthcenterandtheorbitinclinationsothattherelativemotiondynamicsmodelcanbesolvedandtheanalyticalrelativemotionequationscanbeobtainedunderJ2perturbationforcewhenthereferenceorbitiscircularorellipticalwithverysmalleccentricity.SimulationsresultsshowthattheprecisionofrelativemotioncanbeimprovedgreatlybycomparingwithCWequations.Itdemonstratestheeffectivenessandveracityofthenewmethod.

Relativemotion; CWequations; J2perturbation;Analyticalequation

*国家自然科学基金(11672293)

2016-11-08

周 敬 (1991-)，男，安徽人，硕士研究生，主要研究方向为飞行器动力学、控制与仿真；郑建华(1966-)，女，河南人，博士，研究员，博士生导师，主要研究方向为飞行器动力学、控制与仿真；李明涛(1982-)，男，河南人，博士，研究员，硕士生导师，主要研究方向为飞行器动力学、控制与仿真。

V412.4

A

1006-3242(2017)02-0044-07