一种卫星遥测参数动态ARMA建模方法*

朱丽莎 姜 斌 程月华 陆宁云

1.南京航空航天大学自动化学院，南京 210016 2.南京航空航天大学航天学院, 南京 210016



一种卫星遥测参数动态ARMA建模方法*

朱丽莎1姜 斌1程月华2陆宁云1

1.南京航空航天大学自动化学院，南京 210016 2.南京航空航天大学航天学院, 南京 210016

针对部分卫星遥测参数序列在长时间演变中其底层数据生成机制与相互关系存在变化的情况，对传统自回归移动平均(ARMA)模型进行改进，提出一种动态ARMA建模方法。该方法根据预测误差来衡量模型对后续数据的“适合度”，并根据适合度对序列进行分割。在序列分割的基础上，不断更新模型，从而实现动态ARMA建模。最后，利用“天巡一号”(TX-1)卫星遥测数据进行验证，结果表明该方法能有效分割序列，提高建模与预测精度。 关键词 时间序列分割；自回归移动平均；建模；遥测数据

卫星在轨运行时，各系统的监测参数通过测控操作下达地面站，形成大量遥测数据。遥测参数预测是状态预测的前提，而状态预测是判断卫星运行是否正常的重要依据，也是可靠性评估、故障预警与预防等研究的重要前提。如何实现卫星遥测参数的精确预测是航天器故障预测与健康管理的核心技术之一[1-5]。

目前，航天器预测领域已有一些研究，预测区间技术、神经网络、支持向量机、ARMA模型和灰色模型等多种方法都有应用[6-23]。文献[8]利用超1000小时的陀螺仪监测数据，拟合得到一个线性高阶多项式方程来预测性能趋势。文献[9]将预测区间技术用于遥测数据趋势预测。Gebraeel和Lawley利用神经网络预测轴承性能退化及剩余寿命[10]。文献[12]将支持向量机回归方法用于性能退化轨迹建模。文献[13]用GM(1,1)模型预测遥测缓变参数。文献[14]进一步用灰色理论进行电子设备在线故障预测。对于卫星遥测数据而言，时间序列法中的ARMA预测是一种常用方法，如文献[16-17]用ARMA模型进行设备故障预测；文献[18]用ARMA模型对卫星遥测数据做短期预测。近几年还出现了结合灰色理论与ARMA模型的组合模型(GM-ARMA)，在各领域都有应用，见文献[19-21]。但由于卫星遥测参数的数据特性复杂，在长时间的演变中，一些参数的底层数据生成机制变化，导致各数据段的数据特性和变化规律不同，简单地对整个遥测参数序列建立单一的静态模型不能得到准确模型。

本文基于传统的ARMA模型，分析这类卫星遥测参数数据特性，研究了改进的动态ARMA建模与预测方法。该方法根据ARMA模型之于序列的“适合度”对遥测参数序列进行分割，建立动态模型逐段描述，提高预测精度。利用南京航空航天大学“天巡一号”(TX-1)卫星遥测数据进行实验，验证了方法的准确性和有效性。

1 问题描述

时间序列预测是预测方法体系中的重要组成部分，其中ARMA模型迄今为止理论最为完善。它的一般形式如下[24]：

Φ(B)xt=Θ(B)at

(1)

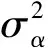
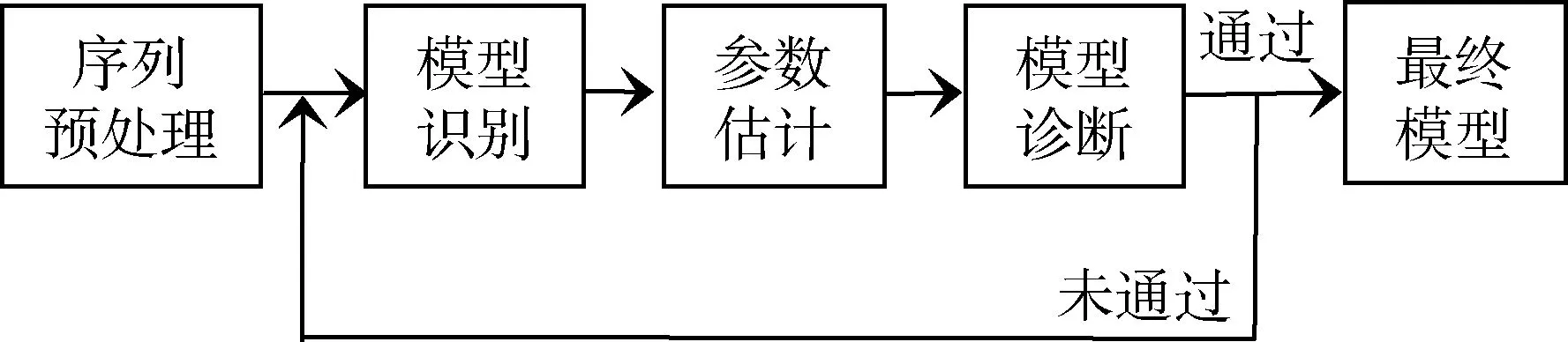
图1 ARMA建模流程图

将式(1)改写成如下形式：

(2)

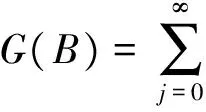
(3)

然而，并不是所有遥测参数都能直接采用传统ARMA模型对整段序列进行描述，有时无法得到准确的模型。如“TX-1”动量轮电机电流序列第117～177天数据最佳模型为ARMA(7,1)，而第178～240天数据最佳模型却为ARMA(8,8)，如果用ARMA(7,1)去描述第178～240天数据，不能通过参数显著性检验(表1)及模型检验(图2)，故不同数据段适合的模型不同。

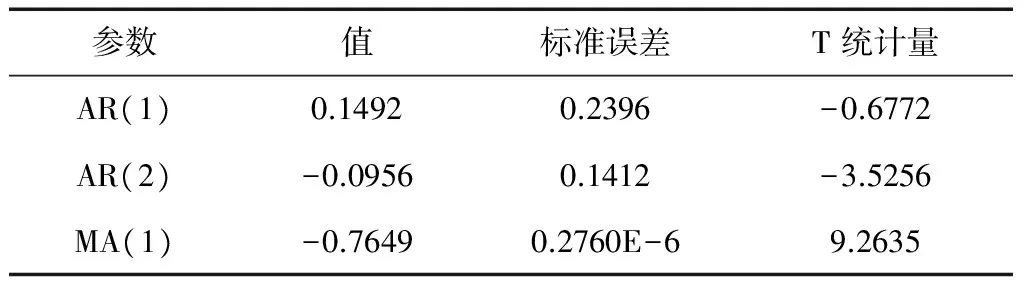
表1 参数检验(第178～240天)

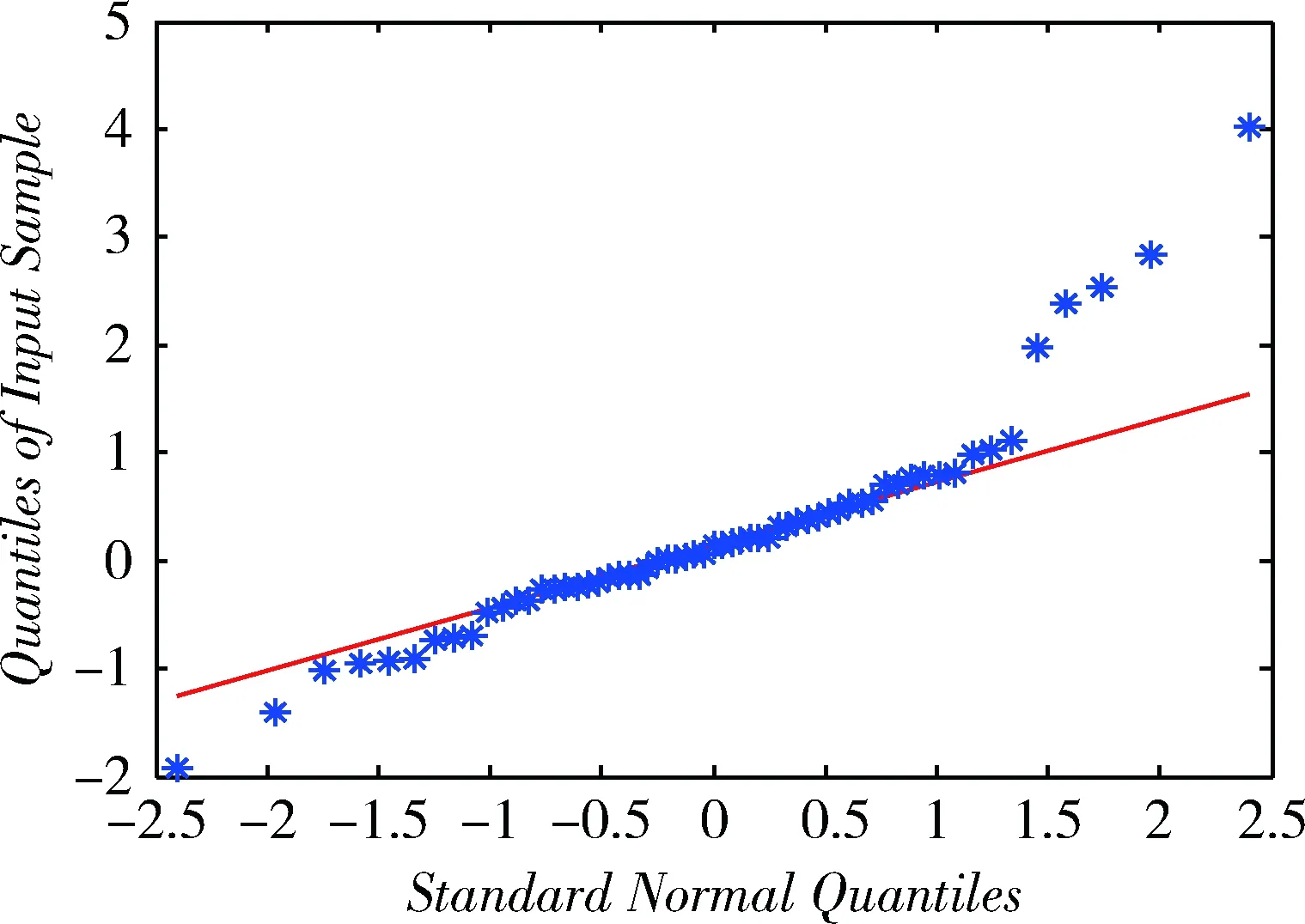
图2 模型检验(第178～240天子序列)

另一方面，对于不同数据段适合的模型不同的情况，如果简单地用单一模型去描述会降低建模精度。如对第1～240天数据建立一个模型，则最佳模型为ARMA(4,4)，但其拟合误差却比子序列模型误差高一个量级(见表2)。对于部分不能直接用单一静态模型描述整个序列的遥测参数，应对序列进行恰当的分割，用各自最适合的模型去描述。

表2 模型与拟合误差

由于卫星遥测数据特性复杂，各种参数的变化情况不同。一些参数在短则数月、长则数年的演变中，随时间推移，其数据底层生成机制可能发生变化，导致各数据段的形态特征和变化规律产生变化。对于这部分参数，如动量轮电机电流、充电电流等，直接用单一静态ARMA建模精度较低，需研究改进的动态方法。本文对这种情况下的遥测参数ARMA建模与预测，增加了基于模型“适合度”的序列分割环节和动态建模环节，获得精度较高的建模和预测结果。

2 改进的动态ARMA模型

基于单一静态模型在部分卫星遥测数据建模中的局限，本节提出改进的动态ARMA模型。改进模块简图如图3。

图3 改进的动态ARMA模型简图

首先基于当前ARMA模型之于后续数据的“适合度”对序列分割，然后根据分割结果和后续数据对模型不断更新完善，最终建立能对遥测数据逐段描述的动态模型，使得建模和预测结果更可靠。

2.1 序列分割环节

动态建模的关键在于序列分割，而序列分割的关键在于判断当前模型是否适合继续描述后续数据。由于ARMA模型描述的是数据底层生成机制和相互关系，当这些发生改变时，适合的模型就可能改变；若当前模型对后续数据的预测误差太大，则说明当前模型已不适合继续描述它们了，应建立更合适的新模型。本文利用序列的历史信息和预测信息计算模型对后续数据的适合度，下面给出其定义。

2.1.1 适合度定义

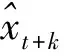
由定义1知，适合度计算需分2种情形讨论：

(4)

(5)

其中，gj,j=1,2,…是模型M的格林系数，Nη/2是使P(N>Nη/2)=η/2的标准正态分布的分位数。

2.1.2 序列分割点算法

算法1 分割点算法

step1 输入Fmin和Ft+i1,,…,Ft+is;

step2 对每个Ft+ik(1≤k≤s)计算：

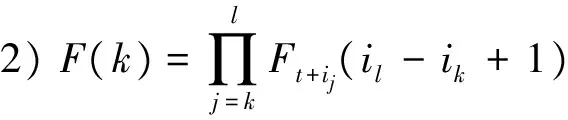
step3 若s<3或is-i1<3，则无需分割。令k=0，输出k，结束算法；否则进行step4；

整个序列分割环节可用流程图4概括。首先，计算预测窗口内每个点的适合度，筛选出适合度小于1的点，然后根据分割点算法确定分割点位置。

图4 分割环节流程图

例如，根据动量轮电机电流第1～50天数据建立模型为ARMA(2,1)，取Fmin=0.01，预测步长h=20，计算出适合度小于1的点,如表3所示。

表3 适合度计算结果

由此算得，F(1)=0.042，F(2)=0.027，F(3)=0.031，F(4)=0.037，其中F(2)最小，所以选择分割点为第65天。

2.2 动态建模环节

卫星遥测数据序列较长，可能产生多个分割点，形成多段子序列。2.1节序列分割环节只确定了1个模型M的1个分割点位置。为了准确描述整个序列，本节要考虑的是确定了分割点位置后，如何利用最新数据对当前模型更新，以及如何对后续数据继续建模的方法，称为动态建模环节。

算法2 动态建模算法

step1 输入遥测序列X={x1,x2,…,xn}，预测步长为h，适合度阈值为Fmin，起始指针v=1，末尾指针w=m；

step2 依次读取m个数据{xv+1,…,xv+m}，对它们建立新模型M，令w=v+m；

step3 计算M的预测窗口内各点适合度，并计算分割点位置k；

step4 若k=0，说明无需分割，则用预测窗口内数据更新模型M，末尾指针w后移k步，转step3；否则转step5；

step5 在第w+k个点处分割，用{xw+1,...,xw+k-1}更新模型M；令v=w+k，转step2；

step6 如此循环直到序列X终点

动态建模算法简化示意图如图5，若M在当前窗口内无分割点，则更新M并继续用M向后描述；若k不为0，则用分割点之前数据更新M，对分割点之后的数据重新建模。重复此过程直到序列终点。

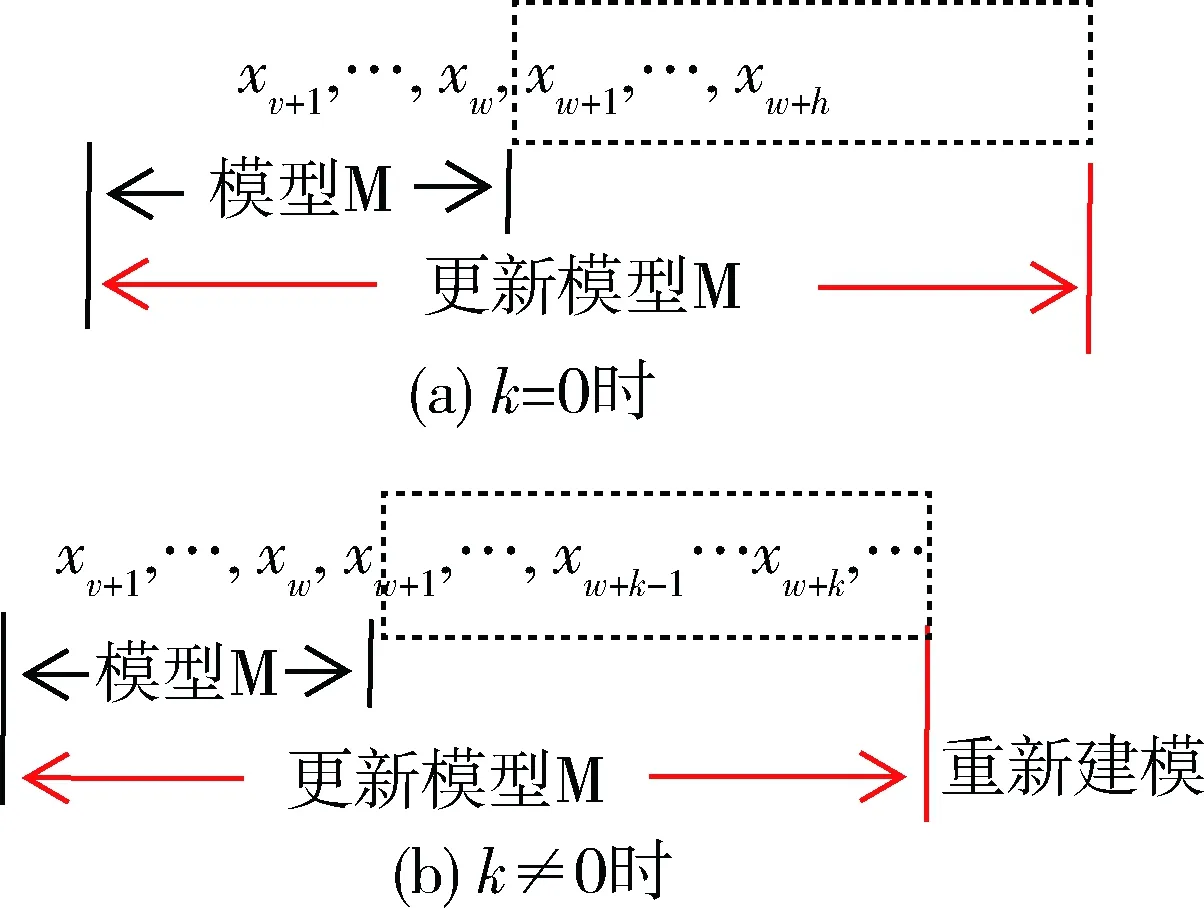
图5 动态建模简化示意图

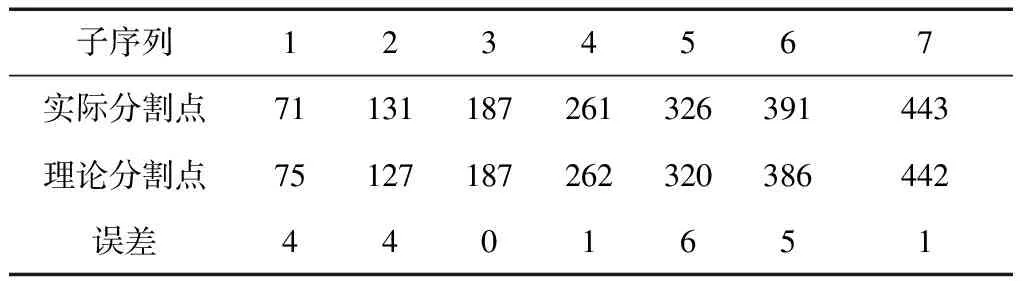
图6是一组根据8个不同ARMA模型事先仿真得到的数据，取Fmin=0.01，窗口长度h=10，根据分割点算法和动态建模算法，得到其理论分割点及分割误差如表4所示。

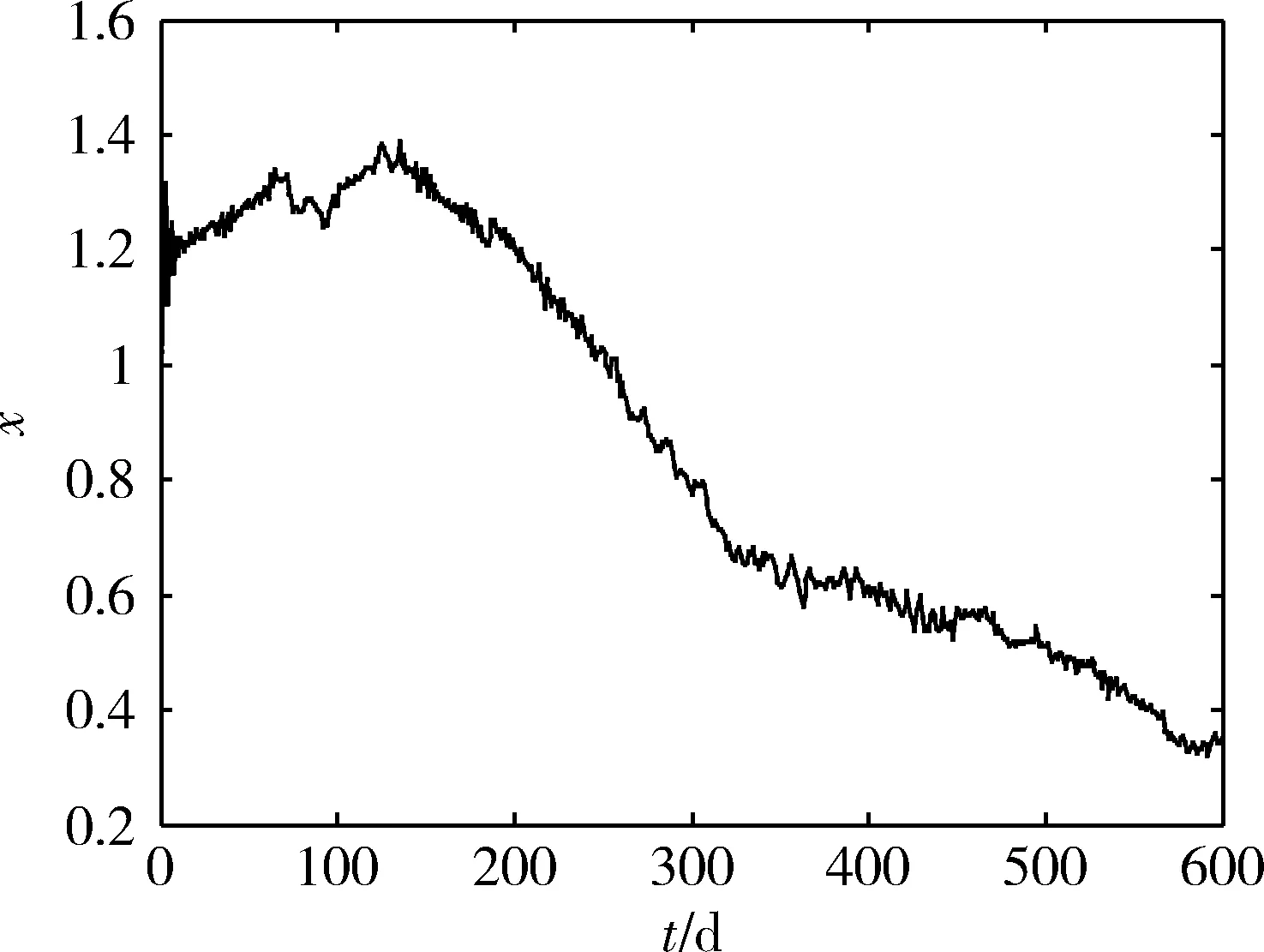
图6 仿真数据

表4 仿真数据的分割误差

子序列1234567实际分割点71131187261326391443理论分割点75127187262320386442误差4401651

上述算法可以较为准确地分割由不同模型生成的子序列。并且，动态建模环节对时间序列的长度无限制，通过序列分割与不断更新模型，提高建模与预测精度，下节将通过实际遥测数据的实验来验证这一点。

3 实验验证及分析

采用南京航空航天大学天巡一号“TX-1”卫星的2个遥测参量动量轮电机电流和充电电流在发射入轨后第1～490天的遥测数据对算法进行实验验证。

3.1 序列分割结果及分析

取Fmin=0.01，预测步长h=10，动量轮电机电流和充电电流序列分割结果分别如图7和8所示，图中竖直虚线为分割线。

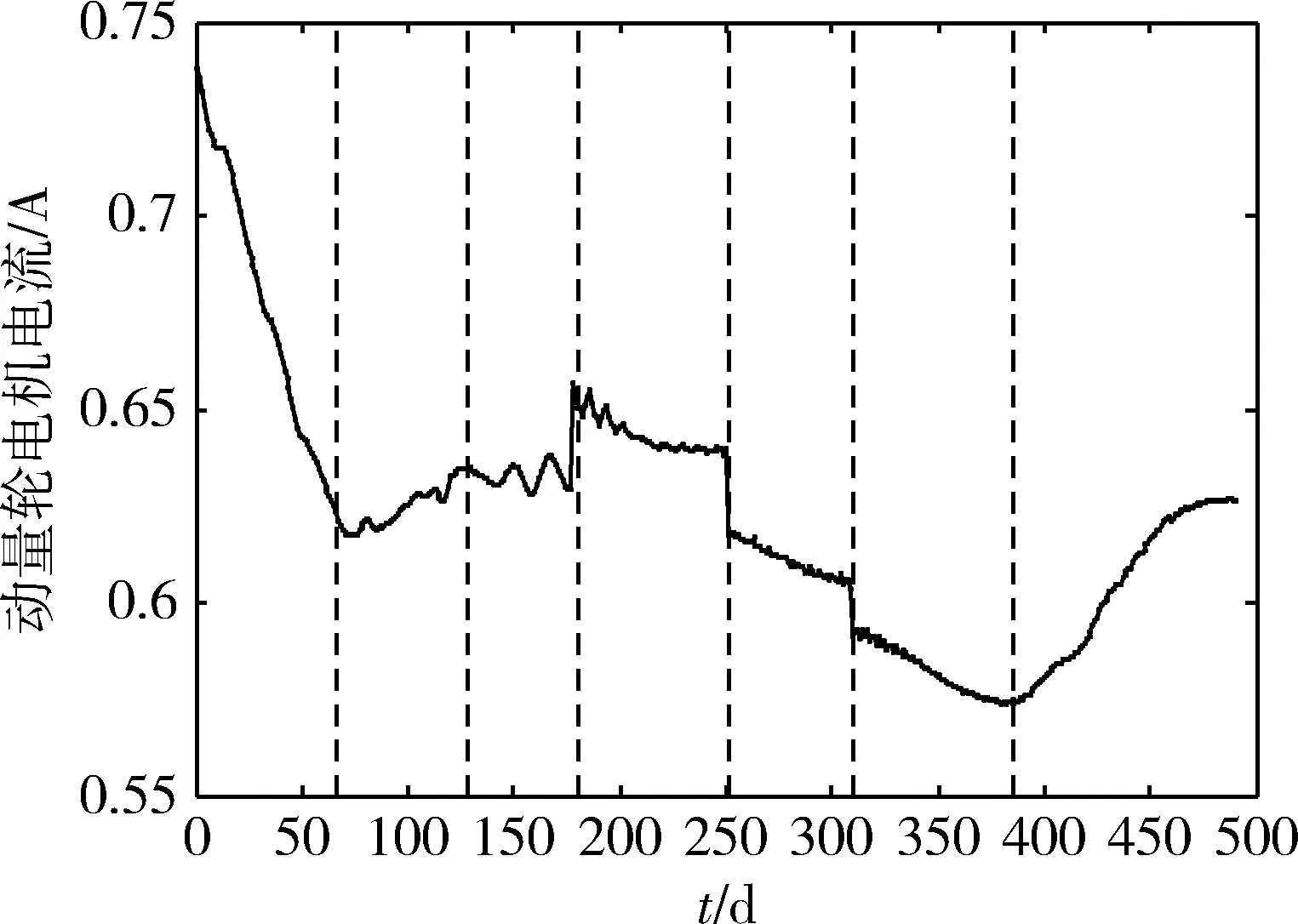
图7 动量轮电机电流序列分割

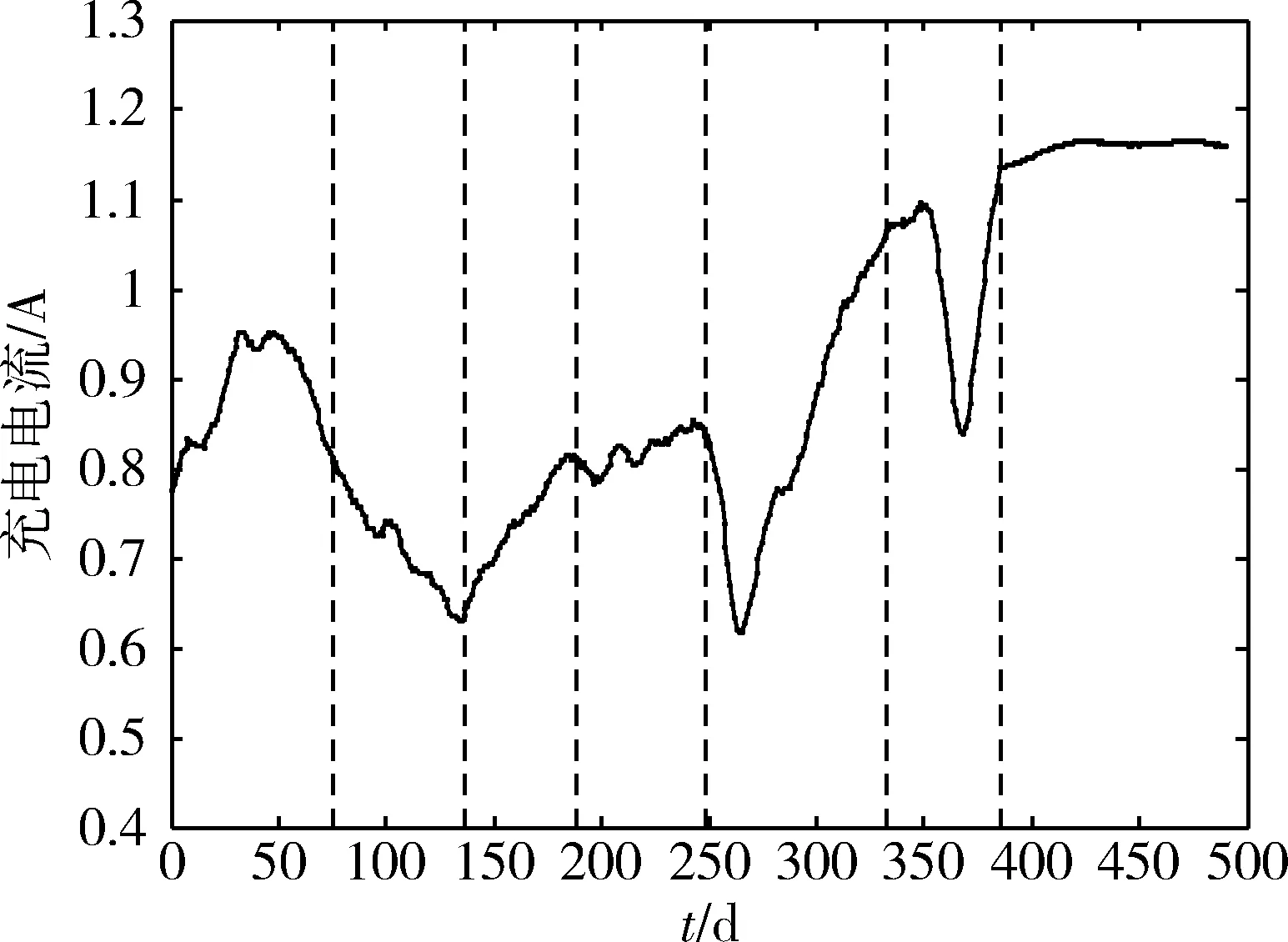
图8 充电电流序列分割

若分割点两侧模型没有明显差异，则认为该分割是错误的。表5所示为各子序列模型的结构，如(p,q)表示模型ARMA(p,q)。从表5可看出，每段子序列所适合的模型都各不相同，无错误分割，表明本文方法能有效分割时间跨度长的卫星遥测数据序列。

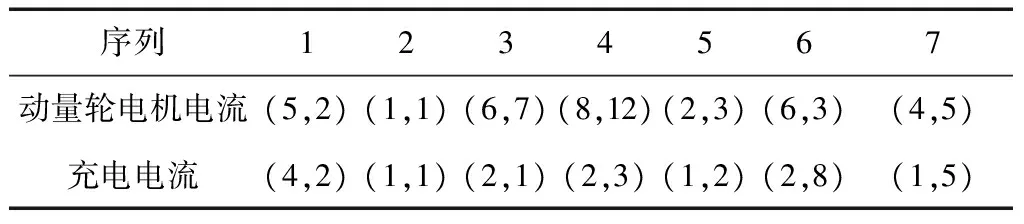
表5 各子序列模型

3.2 预测结果及分析

为了验证本文算法对卫星遥测数据建模的有效性，接下来比较静态ARMA模型、灰色理论与ARMA的组合模型GM-ARMA[19]和动态ARMA模型3种方法的建模效果。一般采用标准误差E来评定模型拟合精度和预测精度。

(6)

(1)建模误差。分别对动量轮电机电流和充电电流第1～480天序列建模。表6所示为不同建模方法的模型拟合误差。

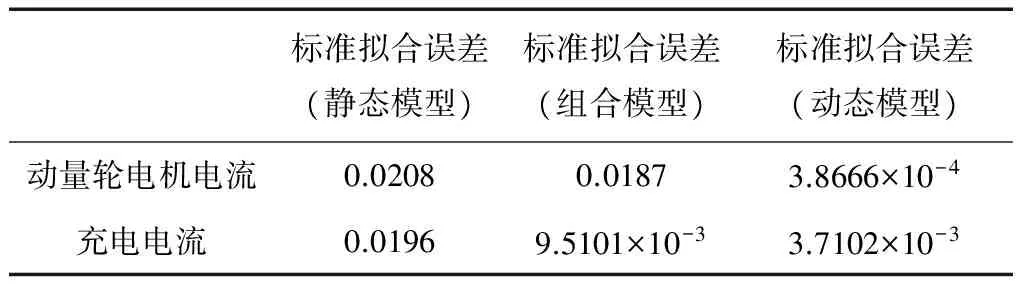
表6 模型拟合误差

从表6可看出，不论是对动量轮电机电流序列，还是充电电流序列，静态模型的拟合误差最大，组合模型次之，而动态模型的拟合误差最小。说明本文动态ARMA方法具有较高的建模精度。

(2)预测精度。对动量轮电机电流和充电电流，分别以2组数据为例对其未来值进行预测，得到结果如图9～12。

图9 动量轮电机电流第481～490天预测结果

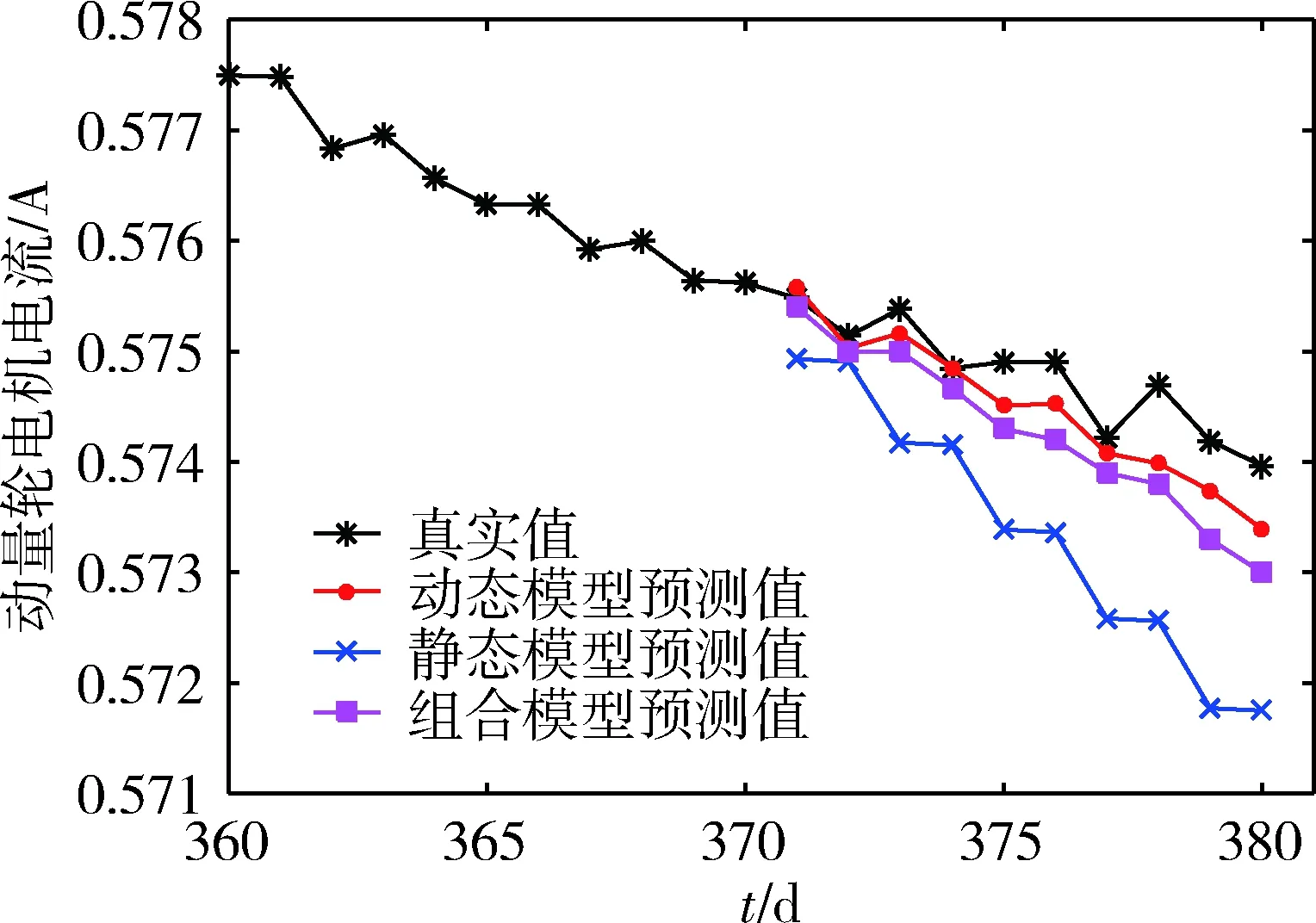
图10 动量轮电机电流第371～380天预测结果

图11 充电电流第481～490天预测结果

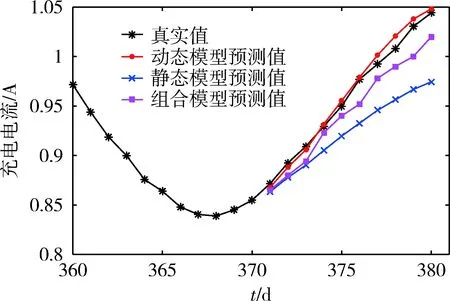
图12 充电电流第371～380天预测结果

从图12可看出，静态模型和组合模型均不能很好地适应当前数据的趋势变化，因为它们是根据序列的整体趋势建立的。相比之下，动态模型的预测曲线更能刻画当前数据的变化趋势，贴合真实数据，具有更高的预测精度。三者的预测误差对比如表7。动态模型的预测误差明显较小。

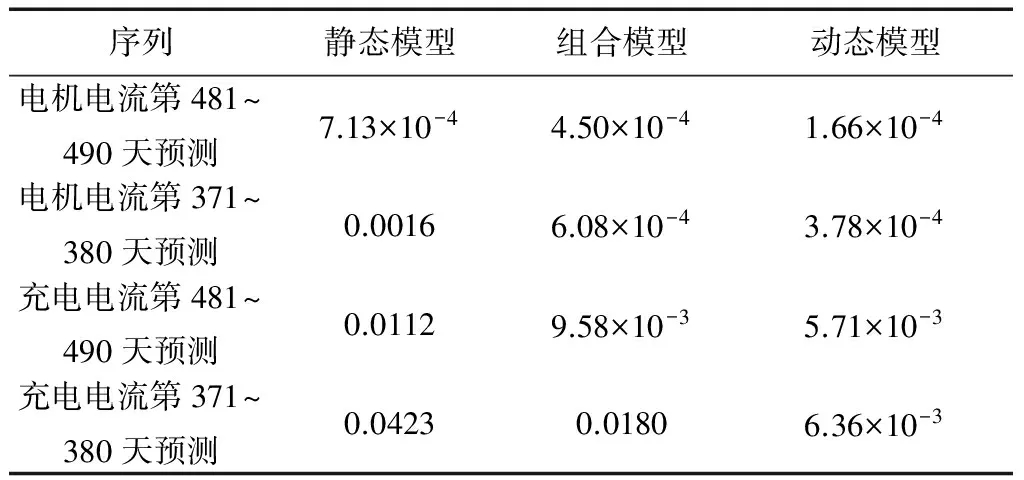
表7 均方根预测误差

综上所述，因空间环境和工作状态变化等，卫星某些遥测参数的底层数据生成机制(DGP)可能发生改变。在该情况下，单一的静态模型不能很好地跟踪序列当前的变化趋势，反而会降低模型的建模与预测精度，而动态模型则正是建立在DGP的动态变化上。仿真结果表明本文所采用的动态建模与预测方法能对序列进行准确的分割，实现较高精度的建模与预测。

4 结论

针对部分卫星遥测参数在长时间演变中其底层数据生成机制可能发生变化，单一的静态模型不能准确描述其变化趋势的情况，基于模型适合度，利用时间序列分割和动态建模的思想进行改进，提出一种动态ARMA建模方法，提高建模精度与预测精度。经实验分析，该方法能对序列进行有效分割、建模与预测，验证了其正确性和有效性。另外，该方法的意义还在于，在此动态模型基础上，可进一步分析分割后各子序列的数据特性之间的差别与联系，为模式识别、相似性分析等研究提供便利，具有一定应用价值。

[1] 刘思峰. 预测方法与技术[M]. 高等教育出版社, 2005.

[2] 程月华, 田静, 陆宁云,等. 基于DTBN的动量轮备份系统剩余寿命预测研究[J]. 航天控制, 2016, 34(3)：89-94.(Cheng Yuehua, Tian Jing, Lu Ningyun, et al. Research on Life Prediction of Momentum Wheels System Based on DTBN[J]. Aerospace Control. 2016, 34(3)：89-94.)

[3] 杨勤荣, 常亮, 张宇宁,等. 航天器综合健康管理技术研究综述[C]. 中国卫星导航学术年会, 2010. (Yang Qinrong，Chang Liang，Zhang Yuning，et al. Survey of Vehicle Health Management Technology Research[C]. China Satellite Navigation Conference,2010.)

[4] Jiang B, Du D, Cocquempot V. Fault Detection For Discrete-time Switched Systems With Interval Time-varying Delays[J]. International Journal of Control Automation & Systems, 2011, 9(2):396-401.

[5] 李学锋, 钱玲. 航天控制系统潜在分析技术应用研究[J]. 航天控制, 2000, 18(1):26-30.(Li Xuefeng, Qian Ling. Applying Research of Sneak Analysis Technique in The Aerospace Control System[J]. Aerospace Control, 2000, 18(1):26-30.)

[6] Fang H Z, Zou K X, Yi D W, et al. The Study of Spacecraft Telemetry Data Prediction Based-on SERTS Model[C]. Prognostics and System Health Management Conference， IEEE, 2011:1-5.

[7] Sary C，Peterson C，Rower J，et al． Trend Analysis For Spacecraft Systems Using Multimodal Reasoning[R]. AAAI Spring Symp Tech report SS-98-04: 157-161．

[8] 徐国平. 基于支持向量机的动调陀螺仪寿命预测方法研究[D].上海交通大学,2008. (Xu Guoping. Research on Life Forecasting Methods of a DTG Based on Support Vector Machine[D]. Shanghai Jiao Tong University, 2008.)

[9] 安伟光, 孙振明, 张辉,等. 预测区间技术在航天器数据处理中的理论与应用研究[J]. 宇航学报, 2006, 27(s1):109-112.(An Weiguang, Sun Zhenming, Zhang Hui, et al. Reserch on Prediction Interval Technology in Applying to Spacecraft Data Processing[J]. Journal of Astronautics, 2006, 27(s1):109-112.)

[10] Gebraeel N, Lawley M, Liu R, et al. Residual Life Predictions From Vibration-based Degradation Signals: A Neural Network Approach[J]. IEEE Transactions on Industrial Electronics, 2004, 51(3):694-700.

[11] 任国恒, 李纲, 贾超超. 一种基于RBF神经网络的遥测数据中长期预测方法[J]. 鄂州大学学报, 2014,(7):94-96.

[12] 胡昌华, 胡锦涛, 张伟,等. 支持向量机用于性能退化的可靠性评估[J]. 系统工程与电子技术, 2009, 31(5):1246-1249. (Hu Changhua，Hu Jintao，Zhang Wei. Reliability Assessment of Performance Degradation Using Support Vector Machines[J]. Systems Engineering and Electronics, 2009, 31(5):1246-1249.)

[13] 金球星. GM(1,1)模型在遥测缓变参数预测中的应用[J]. 科技创新导报, 2012，(16):2-2.

[14] 向刚, 张会彬, 李海孟,等. 基于灰色理论与专家系统的电子设备在线故障预测方法研究[J]. 航天控制, 2013, 31(4):88-92.(Xiang Gang, Zhang Huibin, Li Haimeng, The Research of Electronics Equipment Online Failure Prediction Based on Gray Theory and Expert System[J]. Aerospace Control, 2013, 31(4):88-92.)

[15] 郭小红，徐小辉，赵树强,等．基于新息灰预测的卫星遥测参数状态预测及应用[J]． 宇航学报，2010，31(8) : 1939-1943. (Guo Xiaohong，Xu Xiaohui，Zhao Shuqiang，et al. Satellite Telemetry Parameter Trend Forecast Algorithm Based on New Information and Applications[J]. Journal of Astronautics, 2010，31( 8) : 1939-1943.)

[16] 于勇, 姜兴渭. 基于ARMA模型的卫星故障预测技术应用研究[C]// 全国振动,2000.

[17] 李瑞莹, 康锐. 基于ARMA模型的故障率预测方法研究[J]. 系统工程与电子技术, 2008, 30(8):1588-1591.(Li Ruiyinng, Kang Rui, Research on Failure Rate Forecasting Method Based on ARMA Model[J]. Systems Engineering and Electronics, 2008, 30(8):1588-1591.)[18] 朱晓乐, 王华, 符菊梅,等. 基于ARMA模型的动力系统缓变数据故障趋势预测[J]. 载人航天, 2011, 17(2):54-58.(Zhu Xiaole, Wang Hua, Fu Jumei, et al. Prediction of Slowly Varying Data of Propulsion System Based on ARMA Model[J], Manned Spaceflight, 2011, 17(2):54-58.)

[19] 赵鑫, 郭嘉, 吴建川. ARIMA模型和GM(1,1)与ARMA(p,q)组合模型在滑坡短期预报中的对比分析[J]. 安全与环境工程, 2012, 19(3):24-28.(Zhao Xin, Guo Jia, Wu Jianchuan. Comparative Analysis of ARIMA Model and GM(1,1)-ARMA(p,q) Combination Model in the Short-term Landslide Prediction[J]. Safety and Environmental Engineering, 2012, 19(3):24-28.)

[20] 张巨升. 改进灰色因果时序组合模型在大坝位移监测中的应用研究[D]. 合肥工业大学, 2014.(Zhang Jusheng. The Application of Combination of Improved GM(1,N) Model and Time Series Theory Model on Displacement Monitoring of Dam[D]. Hefei University of Technology, 2014.)

[21] 刘永义, 党亚民, 郑作亚. 一种组合模型在卫星钟差长期预报中的应用研究[J]. 测绘科学, 2012, 37(2):17-19.(Liu Yongyi, Dang Yamin, Zheng Zuoya. Application of a Combined Model in Satellite Clock Bias Prediction[J]. Science of Surveying and Mapping, 2012, 37(2):17-19.)

[22] Orchard M E, Vachtsevanos G J. A Particle Filtering Approach for On-Line Failure Prognosis in a Planetary Carrier Plate[J]. International Journal of Fuzzy Logic & Intelligent Systems, 2007, 7(4):221-227.

[23] Losik L. Stopping Launch Pad Delays, Launch Failure, Satellite Infant Mortalities and On-orbit Satellite Failure Using Telemetry Prognostic Technology[C]. Proceedings of the International Telemetry Conference, 2007.

[24] 魏武雄, 刘超校, 易丹辉. 时间序列分析——单变量和多变量方法(第二版)[M]. 中国人民大学出版社, 2009.

[25] 黄超. 基于特征分析的金融时间序列挖掘若干关键问题研究[D]. 复旦大学, 2005. (Huang Chao. Research on Several Key Issues in Financial Time Series Mining Based on Feature Analysis[D]. Fudan University, 2005.)

[26] Janacek G. Time Series Analysis Forecasting and Control[J]. Journal of the Operational Research Society, 1971, 22(2):199-201.

A Dynamic ARMA Modeling Method for Satellite Telemetry Data

Zhu Lisha1， Jiang Bin1，Cheng Yuehua2，Lu Ningyun1

1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China 2. College of Astronautics, Nanjing University Aeronautics and Astronautics, Nanjing 210016, China

Sincesomesatellitetelemetryparametersequences’underlyingdatageneratingschemeandcorrelationscanbechangedovertime,thetraditionalautoregressionmovingaverage(ARMA)modelisimprovedandasatellitetelemetryparameterdynamicARMAmodelingandpredictionmethodareproposedinthispaper.Aconceptofmodelbasedonpredictionerrorforsubsequentdata“fitness”calculatedisintroduced.Accordingto“fitness”,thesequenceissegmented.Onthebasisofsequencesegmentation,theARMAmodelisupdatedconstantly.Therefore,thedynamicARMAmodelingandpredictionisachieved.Finally,anexperimentisimplementedbyusingdatafromsatellite“TX-1”.Theresultsshowthatthesatellitetelemetrysequencecanbeeffectivelysegmentedandtheaccuracyofmodelingandpredictionisincreasedbyusingtheimprovedmethod.

Timesequencesegmentation; ARMA;Modeling;Telemetrydata

* 国家自然科学基金(61673206)；西安卫星测控中心基金项目；中央高校基本科研业务费专项资金资助(2016083)

2016-11-25

朱丽莎 (1992-)，女，湖南人，硕士研究生，主要从事故障诊断与容错控制研究；姜 斌(1966-)，男，江西人，教授，主要从事故障诊断与容错控制研究；程月华(1977-)，女，安徽人，副研究员，主要从事小卫星姿态控制、故障诊断与容错控制研究；陆宁云(1978-)，女，江苏人，教授，主要从事故障诊断与预测研究。

V44

A

1006-3242(2017)02-0037-07