GNSS信号捕获精化算法研究

吴 镇 周蓓蓓

1．上海机电工程研究所，上海200233 2.南京理工大学，南京210094



GNSS信号捕获精化算法研究

吴 镇1周蓓蓓2

1．上海机电工程研究所，上海200233 2.南京理工大学，南京210094

为了提升捕获中获得的载波频率精度，传统捕获算法通常采用增加信号相关积分时间的方式，这导致计算量大幅增加，硬件要求也要提高以满足导航实时性需要。因此，提出了一种新的方法：在信号捕获成功之后加入精化环节，提升捕获环节获得的载波频率精度。阐述了精化算法的原理及其数学分析方法，进行了实验验证，结果证明了该捕获精化算法的有效性。 关键词 卫星导航；捕获；载波频率；精化算法

当前提高捕获环节获得的载波频率精度的主要方法是提高相关积分时间，这将导致计算量增加和捕获时间延长，难以保证导航的实时性；并且由于相关时间的延长增加了数据位跳变的可能性，导致捕获结果变差。本文在粗捕获成功后加入精化过程，提高捕获获得的载波频率精度，减小相对长时间相关积分的捕获算法的计算量。

1 传统方法

一般来说，捕获环节获得的载波频率精度是中频信号相关积分时间的倒数。如果相关积分时间为1ms，捕获得到的载波频率精度是1000Hz；如果想使捕获得到的载波频率精度达到100Hz，相关积分时间必须为10ms。为了获得比较精确的载波频率，传统捕获方法一般是对信号进行长时间相关积分，大大增加运算量，且由于相关积分时间的延长，增加了数据码发生跳变的概率，导致捕获结果变差。对此，本文提出了一种计算量较小、数据码跳变影响较小、获得载波频率比较精确的方法，即在捕获成功基础上增加一个精化环节。

2 精化算法

2.1 精化算法简述

在捕获成功之后，增加一个精化阶段。精化环节通过对搜索频率间隔的逐次减小，提高搜索频率的精度。

设捕获到的频率是f，对于新的一帧中频信号，同时利用频率为f，f-fs，f+fs的3个分量，并对初始相位为0，π/4，π/2，3π/4的分量进行载波去除并积分，共计12次，求出上述计算中积分对值最大的一次，其相应的频率分量作为新的频率，随后fs减半，对下一个新进的帧迭代精化。fs初值设为500Hz。经过2次迭代，频率精度可到62.5Hz。精化算法流程如图1所示。

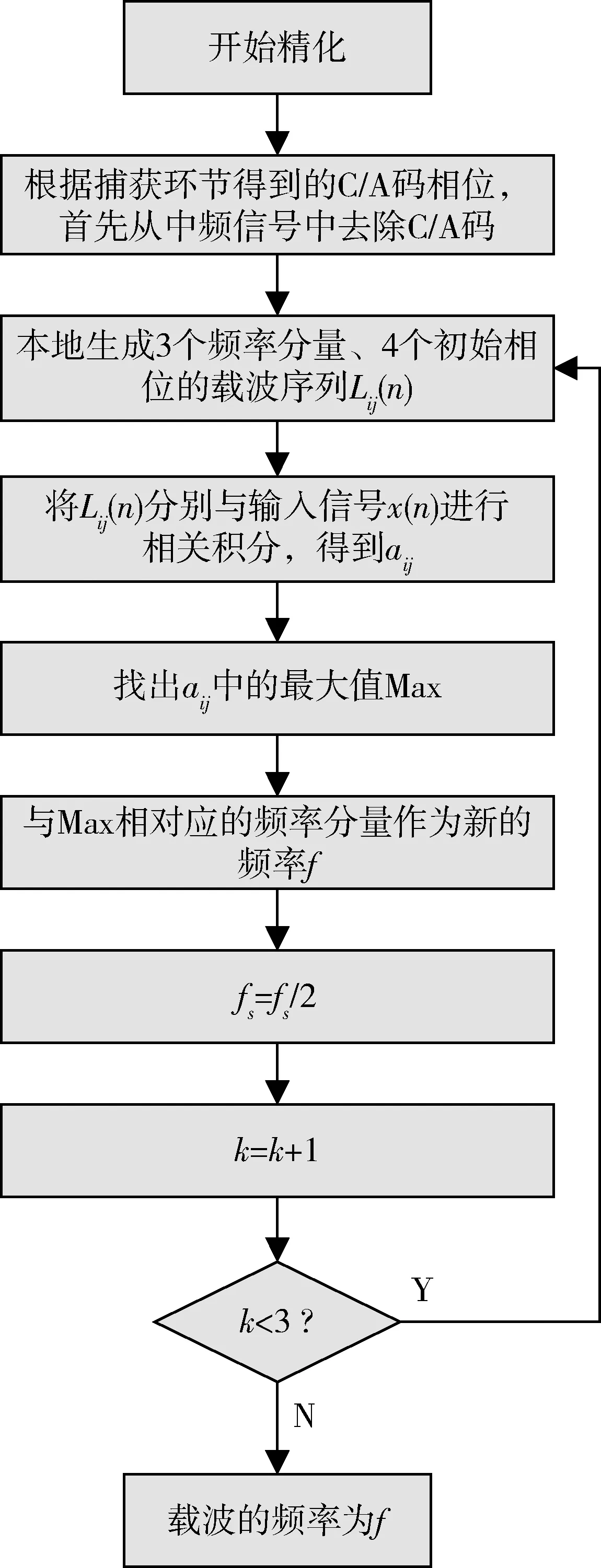
图1 精化算法流程图

在进行实际信号捕获时，由于在捕获环节已得到了CA码的离散信号点，因此精化环节的CA码数字点不用再次生成。由于本地CA码的FFT变换是捕获环节计算量最大的，对此精化算法亦不用重复计算。因此精化环节的计算量大大减小。

正弦信号的自相关函数与相关积分是对应的，本文将从理论上利用正弦信号的自相关函数来分析捕获过程中的相关积分，进而研究GNSS载波精化算法所能达到的精度。下面通过理论与实验验证分析正弦信号的相关积分与自相关函数的关系。

2.2 正弦信号相关积分的结果

正弦信号离散化后相关积分结果如图2所示，图2的局部图如图3～5所示。其中正弦信号幅值为1、频率f=1.405MHz、积分时间长度T=1ms，A/D采样频率为5.714MHz。由局部图可见，随着正弦信号频率误差和相位误差的减小，相关峰值不再明显，再加上噪声干扰的影响，限制了精化算法得到的载波频率精度的进一步提高。

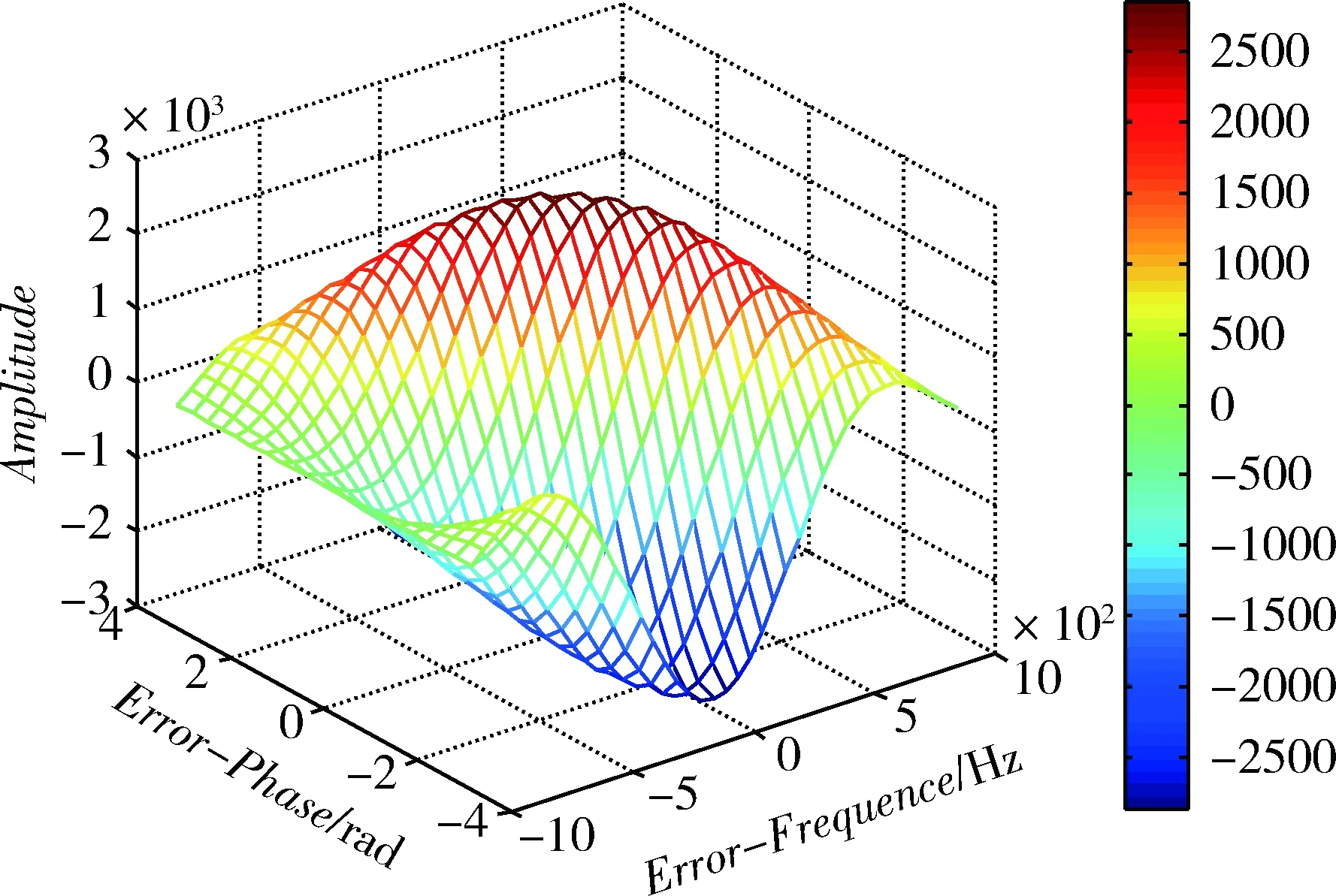
图2 频率差值范围为1000Hz时的自相关值

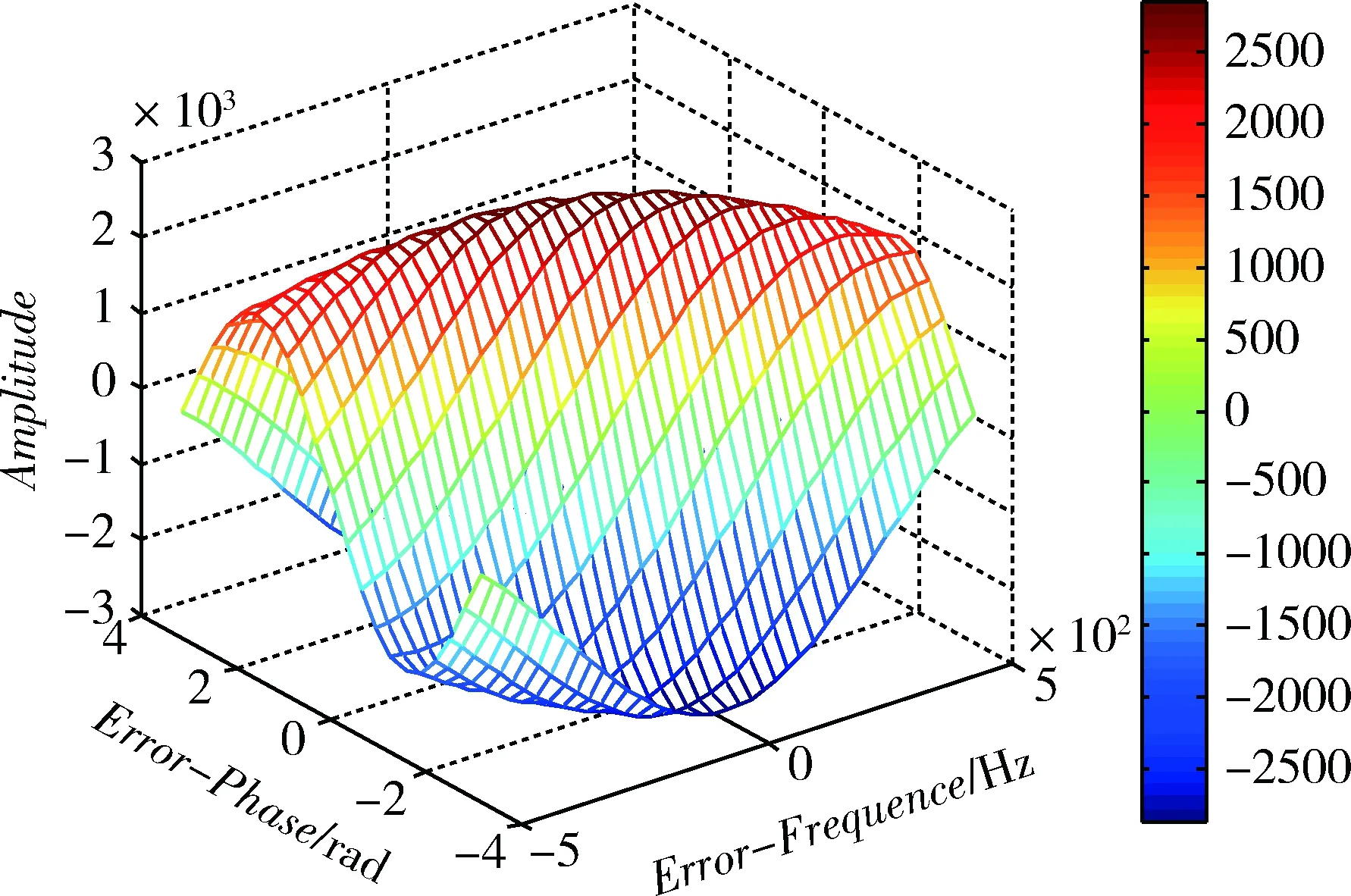
图3 频率差值范围为500Hz时的自相关值

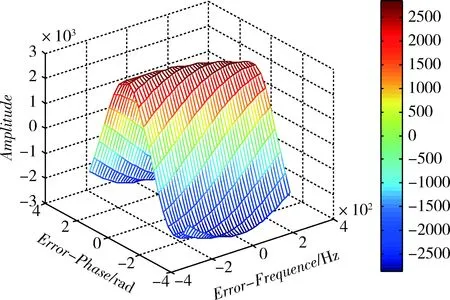
图4 频率差值范围为250Hz时的自相关值

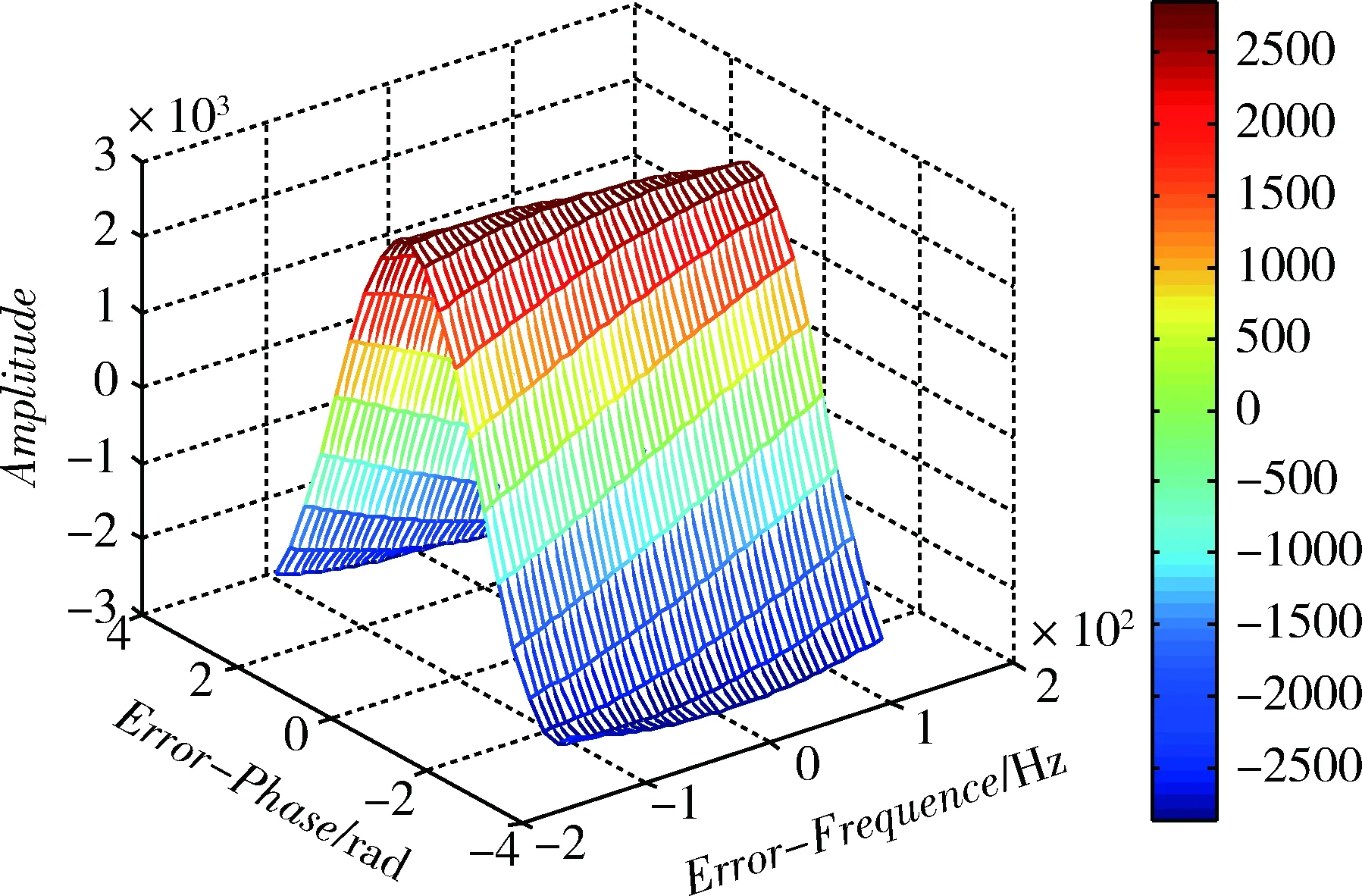
图5 频率差值范围为125Hz时的自相关值

2.3 正弦函数的自相关函数

分析正弦函数的自相关函数与相关积分的关系，使用自相关函数分析精化环节得到的载波频率精度。

2.3.1 正弦函数自相关函数的数学推导

正弦函数的自相关函数:

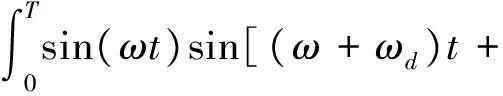
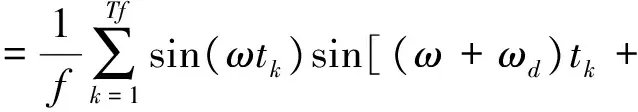
即自相关函数与相关积分通过A/D采样频率联系起来，因此可以使用正弦信号的自相关函数来分析相关积分，进而分析精化环节的精度。

经过推导得到正弦函数的自相关函数为：

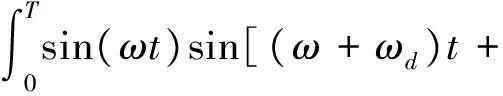
正弦函数的自相关函数值如图6所示，其中正弦信号幅值、频率和积分时间同2.2节所示。

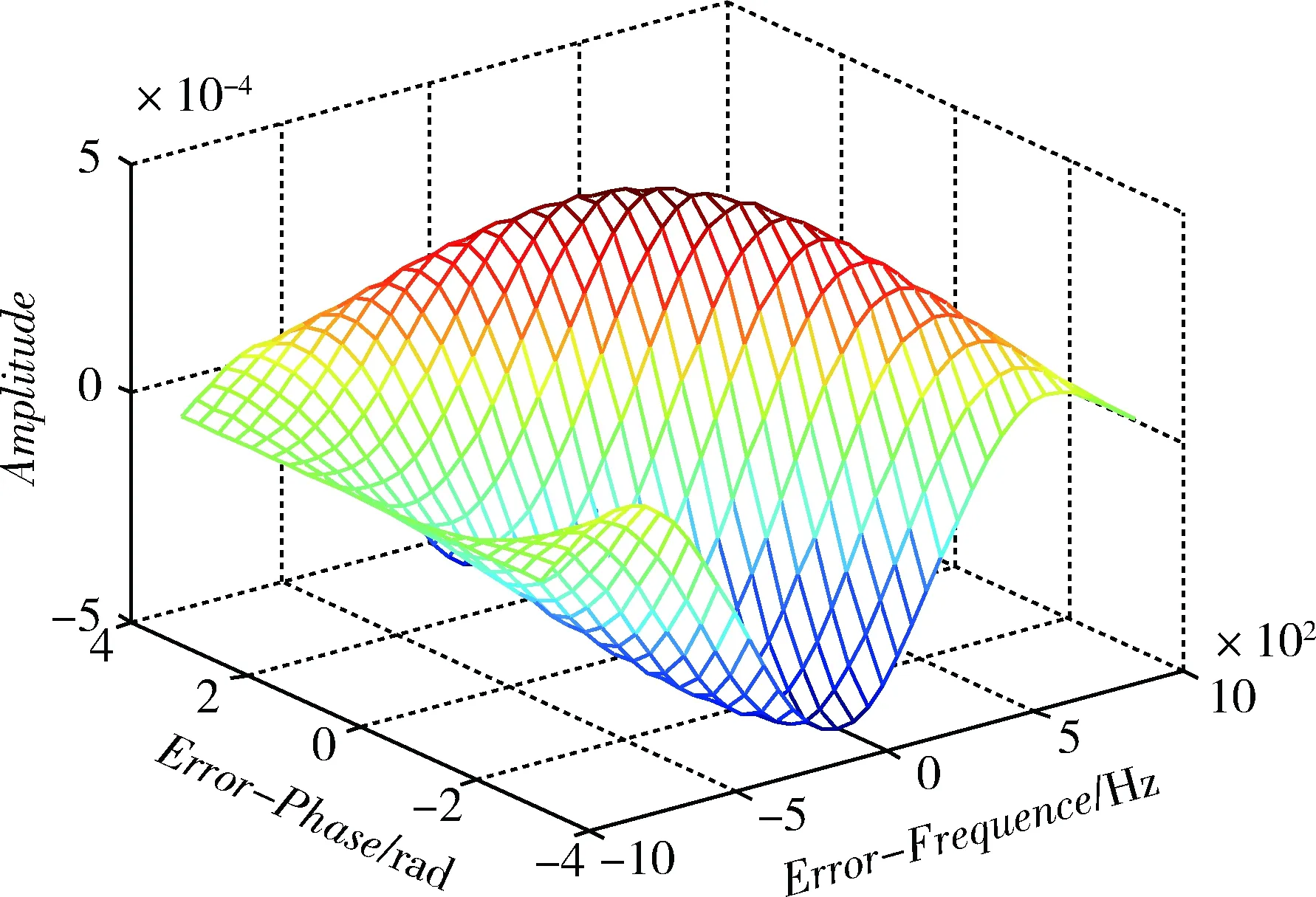
图6 频率差值范围为1000Hz时的自相关值

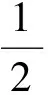
当ωd=φd=0时，

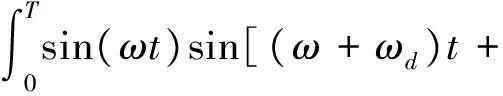
仿真结果与理论分析一致。因此，当GNSS接收机硬件前端的A/D采样频率增大时，进行相关的点数增多，捕获峰值越大，越有利于信号的捕获。

下面分析正弦函数的自相关函数在极值点附近的曲率，即自相关函数的导数，来定性分析精化环节能得到的载波频率精度的极限值。

2.3.2 正弦信号自相关函数的导数

经过推导得到自相关函数对于频率偏差ωd的导数为：

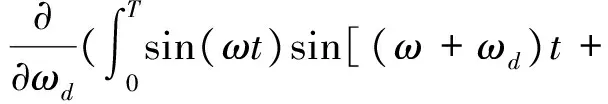
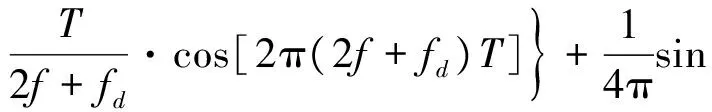
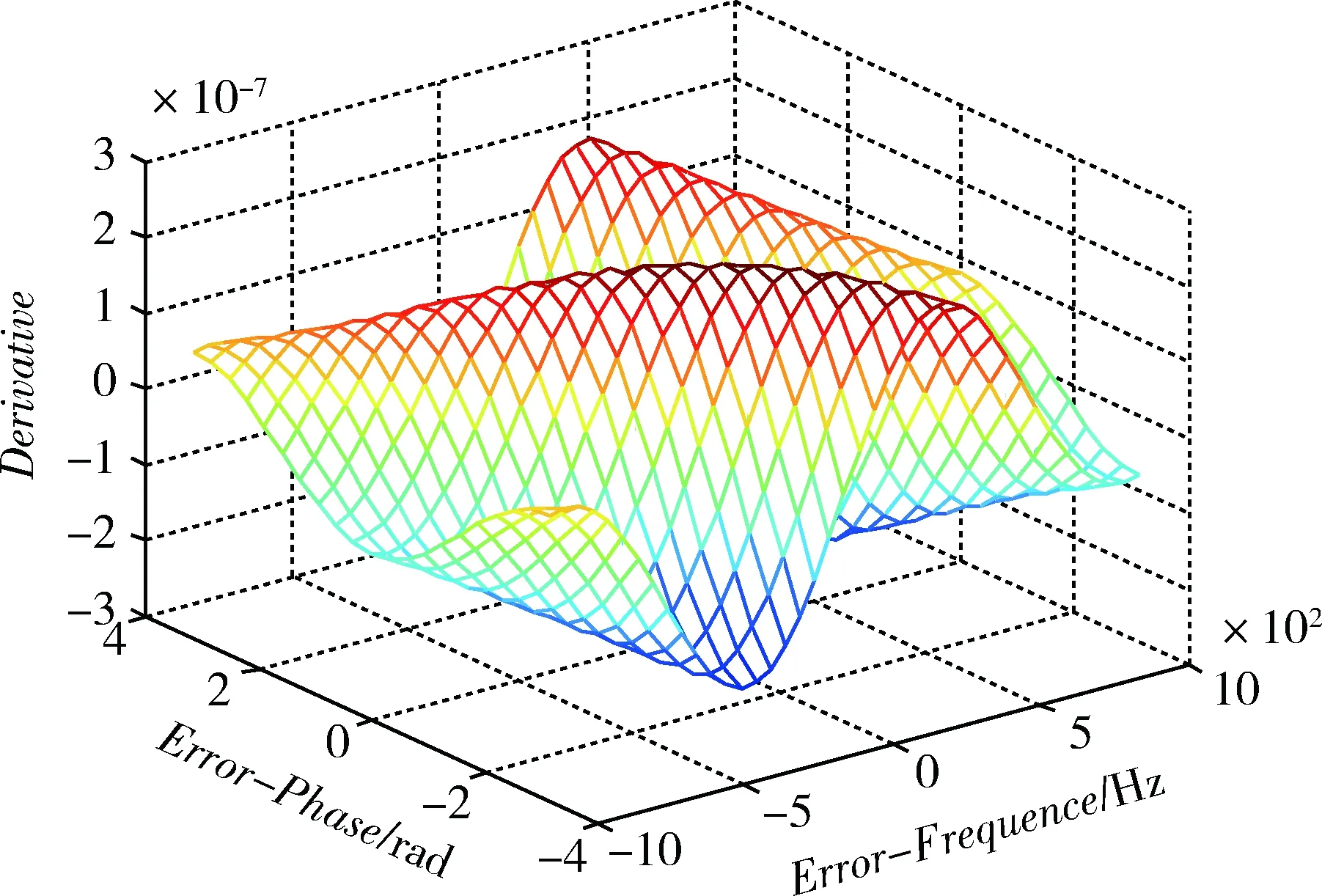
图7 正弦函数自相关函数的导数值

图8 正弦函数自相关函数导数值乘以采样频率图

正弦函数的自相关函数的导数如图7所示，正弦函数的自相关函数的导数乘以A/D采样频率的结果如图8所示。通过计算得到：当相位误差为0～π，频率误差为-120～120Hz，频率变化50Hz时，自相关函数值至少变化100，此数值在捕获时能分辨出来，即通过捕获环节得到的载波频率可以精确到50Hz。

2.4 实验验证

实验条件如表1所示，中频信号模拟器生成的卫星仰角方位图如图9所示。

表1 实验条件

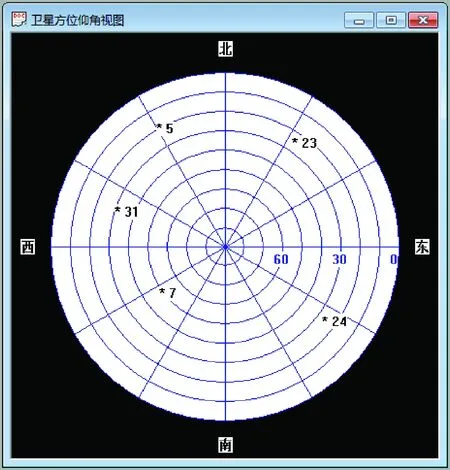
图9 卫星仰角方位图

表2 载波频率

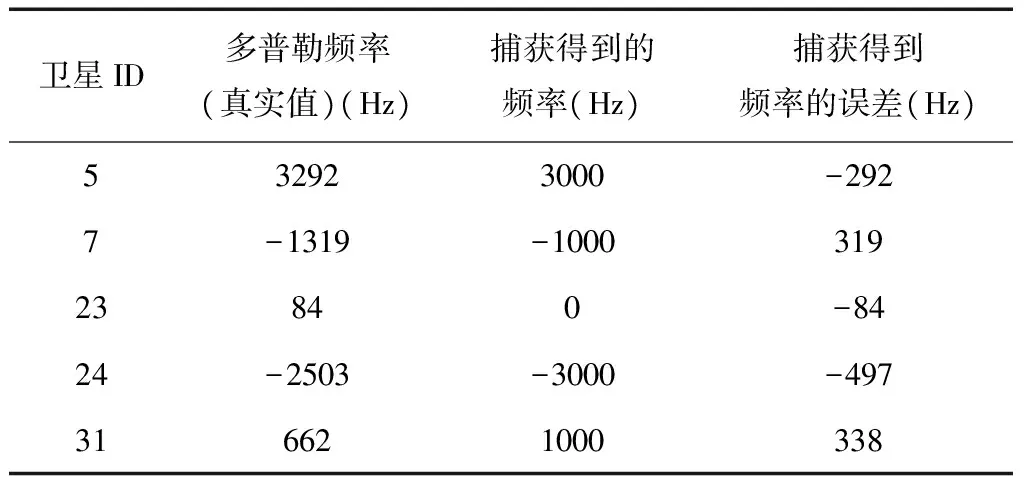
卫星ID多普勒频率(真实值)(Hz)捕获得到的频率(Hz)捕获得到频率的误差(Hz)532923000-2927-1319-100031923840-8424-2503-3000-497316621000338

精化环节迭代3次、载波相位步进为π/4时，得到的载波频率及其误差见表3。

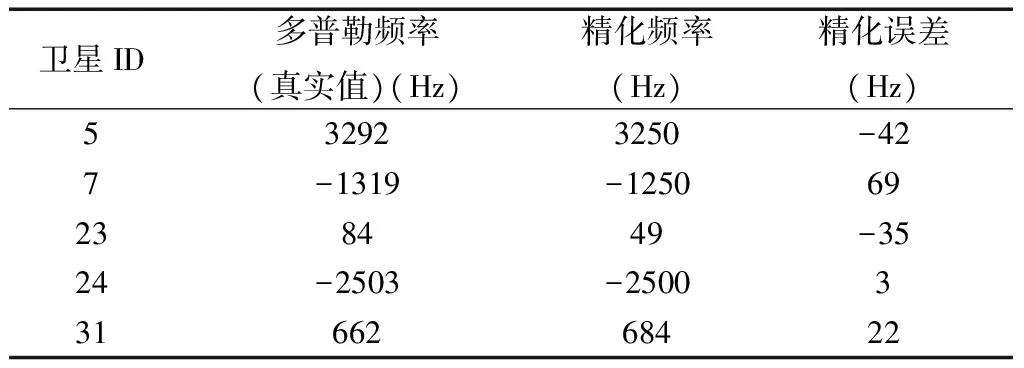
表3 精化频率及其误差

精化环节迭代3次、载波相位步进为π/8时，得到的载波频率及其误差见表4。

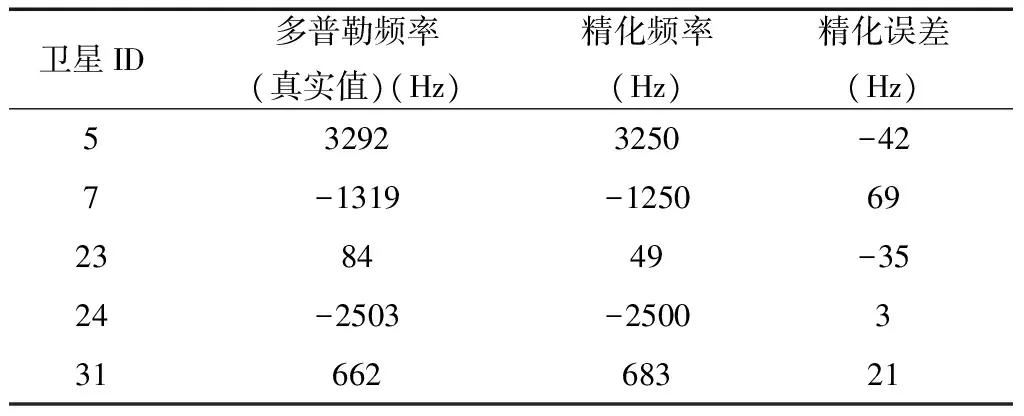
表4 精化频率及其误差

精化环节迭代4次、载波相位步进为π/4时，得到的载波频率及其误差见表5。

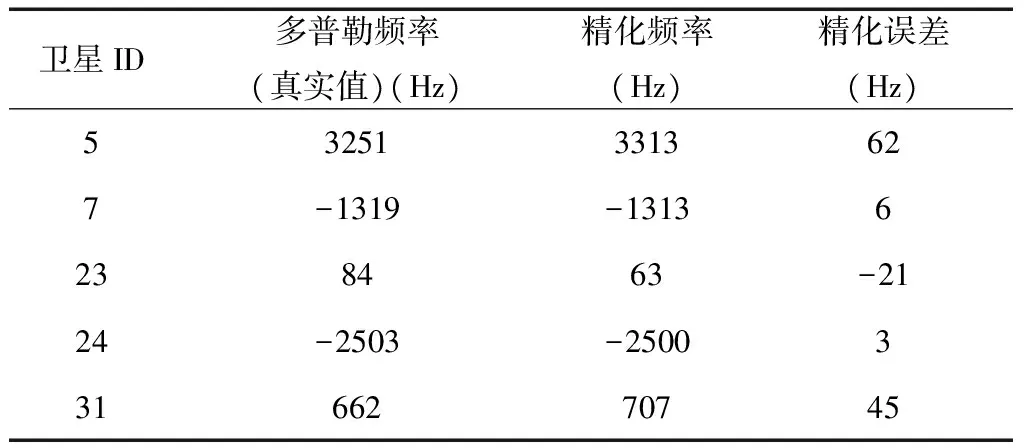
表5 精化频率及其误差

精化环节迭代4次、载波相位步进为π/8时，得到的载波频率及其误差见表6。

表6 载波频率

从表中可以看出： 1)捕获环节得到的载波频率误差的绝对值都小于500Hz，由相关积分时间为1ms决定；2)精化后得到的载波频率误差均小于62.5Hz，结果与前面的理论分析一致；3)经过精化环节之后，相对原来的捕获环节，载波频率精度大大提升； 4)精化环节迭代4次相对于3次，精化误差有提升，但不明显； 5)载波相位步进π/8相对于相位步进为π/4，精化误差提升不明显。因此迭代次数为3次、载波相位步进为π/4的组合从精度和计算量的综合考虑是最优的。

采用C/A码相乘和快速傅里叶变换(FFT)的方法进行1颗卫星的捕获，当A/D采样频率为5.714MHz时，3种捕获方法的计算量和捕获精度分别为： 1)相关积分长度为1ms的捕获：要进行5714次操作，每次操作包括5714点的乘法和5714点的FFT。获得的载波频率精度为1000Hz[1]；2)相关积分长度为10ms的捕获：要进行5714次操作，每次操作包括57140点的乘法和57140点的FFT。获得的载波频率精度为100Hz[1]；3)本文所述相关积分长度为1ms、加入精化环节的捕获方法：首先要进行5714次操作，每次操作包括5714点的乘法和5714点的FFT；其次需要进行36次的5714点的乘法。获得的载波频率精度为62.5Hz。可见，使用本文所述方法，一方面载波频率精度相对传统方法有较大提升；另一方面，计算量相较传统捕获方法增加很少，满足实时性的要求。

3 结论

传统捕获算法采用增加信号相关积分时间提高载波频率，导致计算量大幅增加，不能满足导航实时性的要求，对此提出了一种新的方法：在捕获环节后加入精化环节，进一步精化捕获环节得到的载波频率，以获得比较精确的载波频率。详细阐述精化算法的原理，进行了实验验证，结果证明了捕获精化算法的有效性。本文有2个创新点：1)在捕获成功后加入精化环节来提高载波频率的精度，而计算量增加很少，满足实时性要求； 2)提出了使用正弦函数自相关函数分析捕获得到的载波频率精度的理论方法。实验结果与理论分析一致，证明了文中提出的精化方法的有效性。

[1] James Bao-Yen Tsui.GPS软件接收机基础(第二版)[M].电子工业出版社：108-132. (James Bao-Yen Tsui. Fundamentals of Global Positioning System Receivers a Software Approach(Second Edition) [M]. Publishing House of Electronics Industry：108-132.)

[2] 曲江华,袁洪,宁百齐. 一种新的软件GPS静态接收机频域跟踪方法[J]. 测绘学报, 2005,34(4)：312-316. (Qu Jianghua, Yuan Hong, Ning Baiqi. A New Tracking Scheme in the Frequency Domain for a Static Software GPS Receiver[J]. Acta Geodaetica et Cartographica Sinica, 2005,34(4)：312-316.)

[3] 蔡凡,尹燕,张秀忠. GPS接收机的中频信号处理算法研究[J]. 天文学进展, 2007,25(1)：84-95.(Cai Fan, Yin Yan, Zhang Xiuzhong. Research on IF Signal Processing Algorithm For GPS Receiver[J].Progress In Astronomy, 2007,25(1)：84-95.)[4] 张勇,林宝军,徐志瀚. 软件GPS接收机信号搜索捕获的仿真实验研究[J]. 系统仿真学报, 2006,18(9)：2646-2649.(Zhang Yong, Lin Baojun, Xu Zhihan. Study on Simulation of Signal Search and Acquisition[J].Journal of System Simulation, 2006,18(9)：2646-2649.)

[5] Akopian D. Fast FFT Based GPS Satellite Acquisition Methods[J] .IEE Proc.-Radar Sonar Navigation, 2005, 152(4):277-286.

[6] Chuang Mingyu, Feng Kaiten. Adaptive GPS Acquisition Technique in Weak Signal Environment[C]. Vehicular Technology Conference, 2006, 6:2612-2616.

Research on Refining Algorithm of GNSS IF Signal Acquisition

Wu Zhen1, Zhou Beibei2

1.Shanghai Electro-Mechanical Engineering Institute, Shanghai 200233, China 2.Nanjing University of Science and Technology, Nanjing 210094,China

InordertoimproveprecisionofcarrierfrequencyduringtheIFsignalacquisition,integrationtimeislengthenedintraditionalmethod.Thus,calculationburdenisaddedandreal-timenavigationcannotbeensured.Astotheissuementioned,anewalgorithmisproposedthatitisarefiningsegmentaddedafteracquisitionandthemoreprecisefrequencyofcarrierisobtained.Therefiningsegment,itsmathbasisandexperimentresultsarediscussedtoprovetheefficiencyofthismethod.

GNSSnavigation；Acquisition；Carrierfrequency；Refiningalgorithm

2016-11-08

吴 镇 (1985-)，男，河北衡水人，硕士，工程师，主要研究方向为惯性导航、卫星导航和组合导航；周蓓蓓 (1983-)，女，江苏盐城人，博士，主要研究方向为微光成像器件机理及应用。

O213.2

A

1006-3242(2017)02-0015-05