超声波液体密度测量的一种声反射系数测定方法
2017-08-07李晓佳刘佳鑫李国锋
李晓佳,刘佳鑫,李国锋*
(1.大连理工大学电气工程学院,辽宁 大连 116024;2.国网辽宁省电力有限公司电力科学研究院,沈阳 110006)
超声波液体密度测量的一种声反射系数测定方法
李晓佳1,刘佳鑫2,李国锋1*
(1.大连理工大学电气工程学院,辽宁 大连 116024;2.国网辽宁省电力有限公司电力科学研究院,沈阳 110006)
用超声波测液体密度时,测量声反射系数是重点。提出一种将半波层反射模型简化后,利用相对稳态幅度测量声压反射系数的方法。将一个较薄固体作为半波层置于被测液体中,两侧对称地放置超声波换能器,换能器一个工作在脉冲回波模式,另一个工作在接收模式。调整信号频率使半波层和被测液体交界面的多重反射波达到最大程度干涉,此时被测液体与半波层之间的声反射系数只与两个换能器在稳态下的回波信号幅度比值有关。因此测得换能器的稳态回波信号幅度比,即可得到声反射系数。此方法简化了原来的半波层反射模型,采取对称布局,利用相对稳态幅度法,简化了理论推导过程,降低了测量上的精度要求。最后文章通过实验验证了方法的正确性。
超声传感器;声反射系数;半波层反射法;简化模型;相对稳态幅度法;液体密度测量
利用超声波测量液体密度的主要方法有声速曲线法、声阻法、波导传播法等。声阻法测量液体密度主要是利用声特性阻抗Z=ρc得到的,其中Z为声阻抗,ρ为液体密度,c为超声波传播速度[1]。超声波从介质1垂直入射介质2时,反射和透射情况如图1所示。图1中Ai、At和Ar分别为入射、透射和反射波幅度。
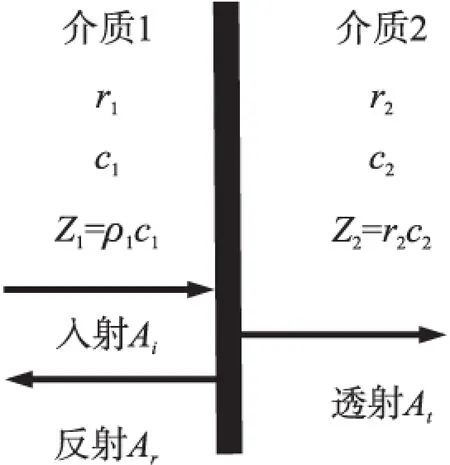
图1 超声波垂直入射时的情况
根据平面波传播理论可知[2],介质1到介质2的声压反射系数R12与介质1和2的声阻抗Z1、Z2的关系为:
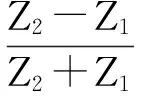
(1)
假设已知介质2的密度ρ2和声速c2,若测得反射系数R12和介质1中的声速c1,则介质1的密度ρ1为:

(2)
以上就是声阻抗法测量液体密度的原理[3]。其中c1可以根据传播距离与时间差计算得到,因此声阻法测量液体密度的关键就是测量声反射系数R12。
测量液体密度时,反射系数R12的测量方法通常借助一个固体延迟材料,即图1中的介质2为延迟材料,介质1为被测液体。被测液体与延迟材料之间的反射系数R12可以根据Ar/At或Ar/Ai得到[4-5]。但固体延迟材料和被测液体声阻抗的差异较大,因此反射系数的测量方法灵敏度较差;有些方法中采用多重反射法,但这样会衰减超声波能量,影响测量结果[6]。
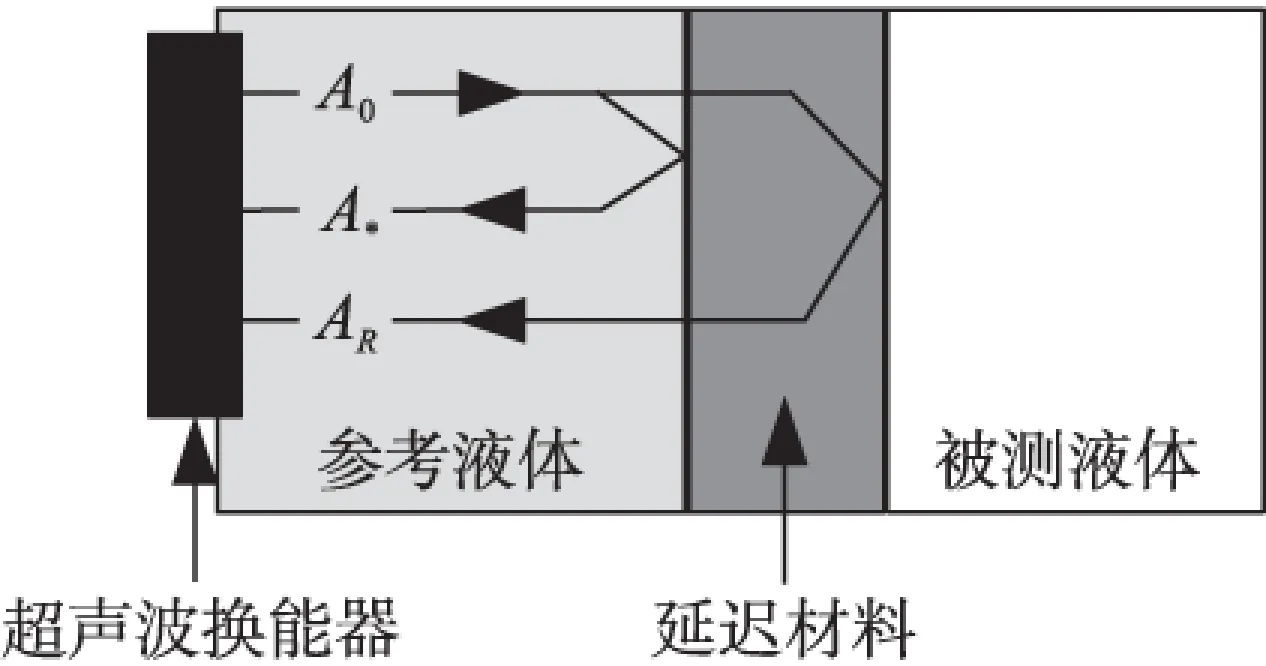
图2 Hirnschrodt设计的反射模型
Hirnschrodt等人[7-8]提出半波层反射模型,如图2所示,图2中A0为入射波幅度,A*为在参考液体与延迟材料交界面处的反射波幅度,AR为在延迟材料和被测液体交界面处的反射波幅度。当换能器的脉冲信号频率f选择正确且驱动脉冲足够长时,A*和AR达到最大干涉,换能器接收的回波信号叠加后趋于稳态,幅度为ASS。当延迟材料厚度l等于声波波长λ的n/2倍(n为正整数),此时延迟材料与参考液体交界面和延迟材料与被测液体交界面这两个表面的回波会产生无损干涉,因此该固体层被称为半波层。此时R12可根据ASS/A0得到,但由于A0的幅值无法在回波信号中直接确定,所以该方法虽然将延迟材料做成半波层,使回波信号叠加后趋于稳态,但还需完善。
刘佳鑫对Hirnschrodt的方法进行了改进[9],在半波层反射法基础上,在被测液体一侧也连接换能器,模型如图3所示。图3中A0为入射波幅值,A1到An为经1至n次反射后换能器A接收到的信号幅值,B1到Bn为经1至n次反射后换能器B接收到的信号幅值。两个换能器接收的回波信号相对稳态幅度分别为ASS和BSS,R12可以由相对稳态幅度比ASS/BSS得到。ASS和BSS计算公式如下:
(3)
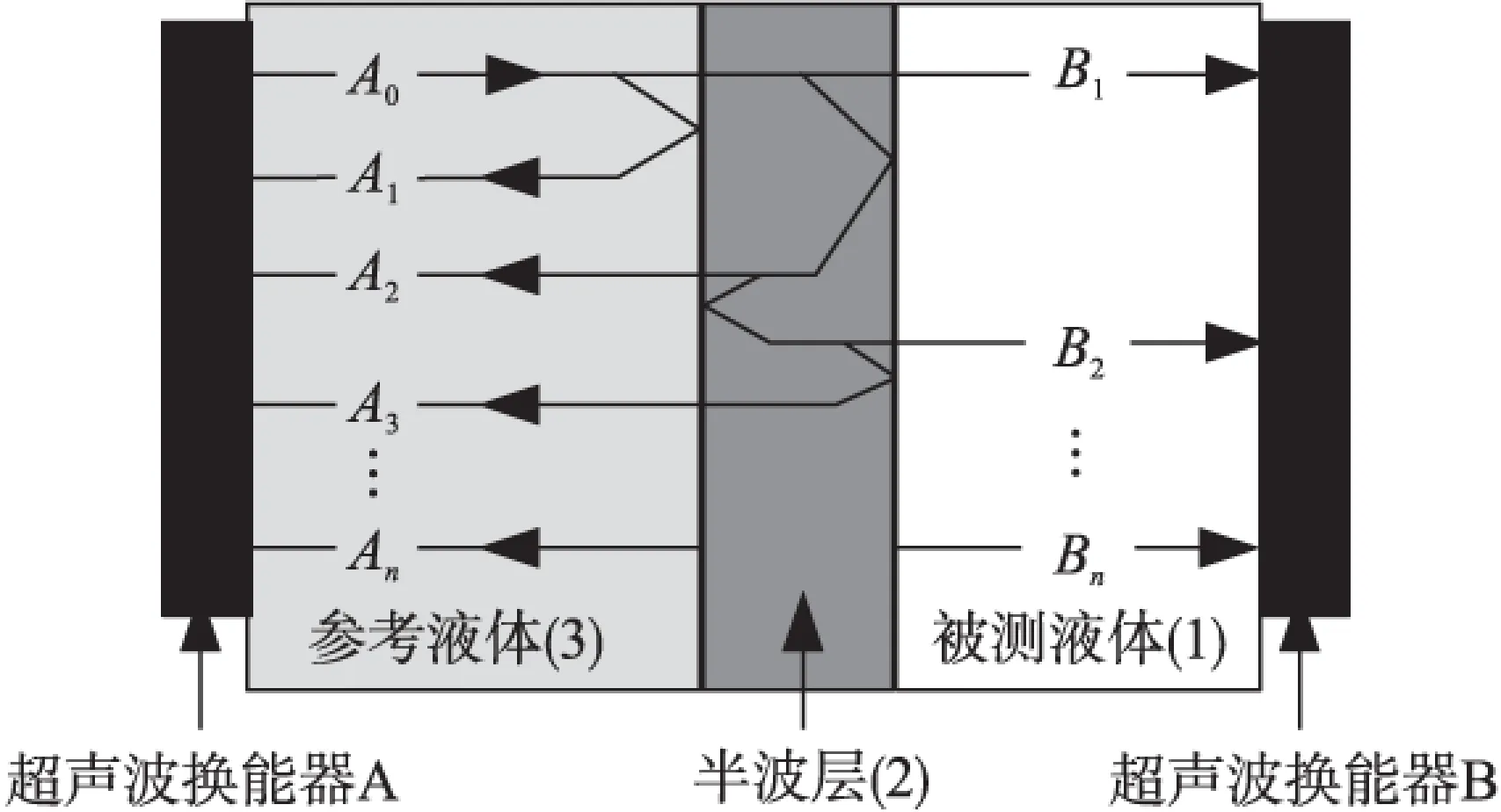
图3 文献9中的半波层反射模型
文献[9]的方法不用直接测量入射波的幅度,而是利用两个超声波换能器的相对稳态幅度比来求声反射系数R12,完善了半波层反射法。
文章对文献[9]所述的半波层反射模型进行了进一步的改进,在保留相对稳态幅度法的基础上,用被测液体替换参考液体,建立对称的简化模型。简化模型中R12的推导过程简单,计算量小,误差也较小,原因将在后续论述中解释说明。
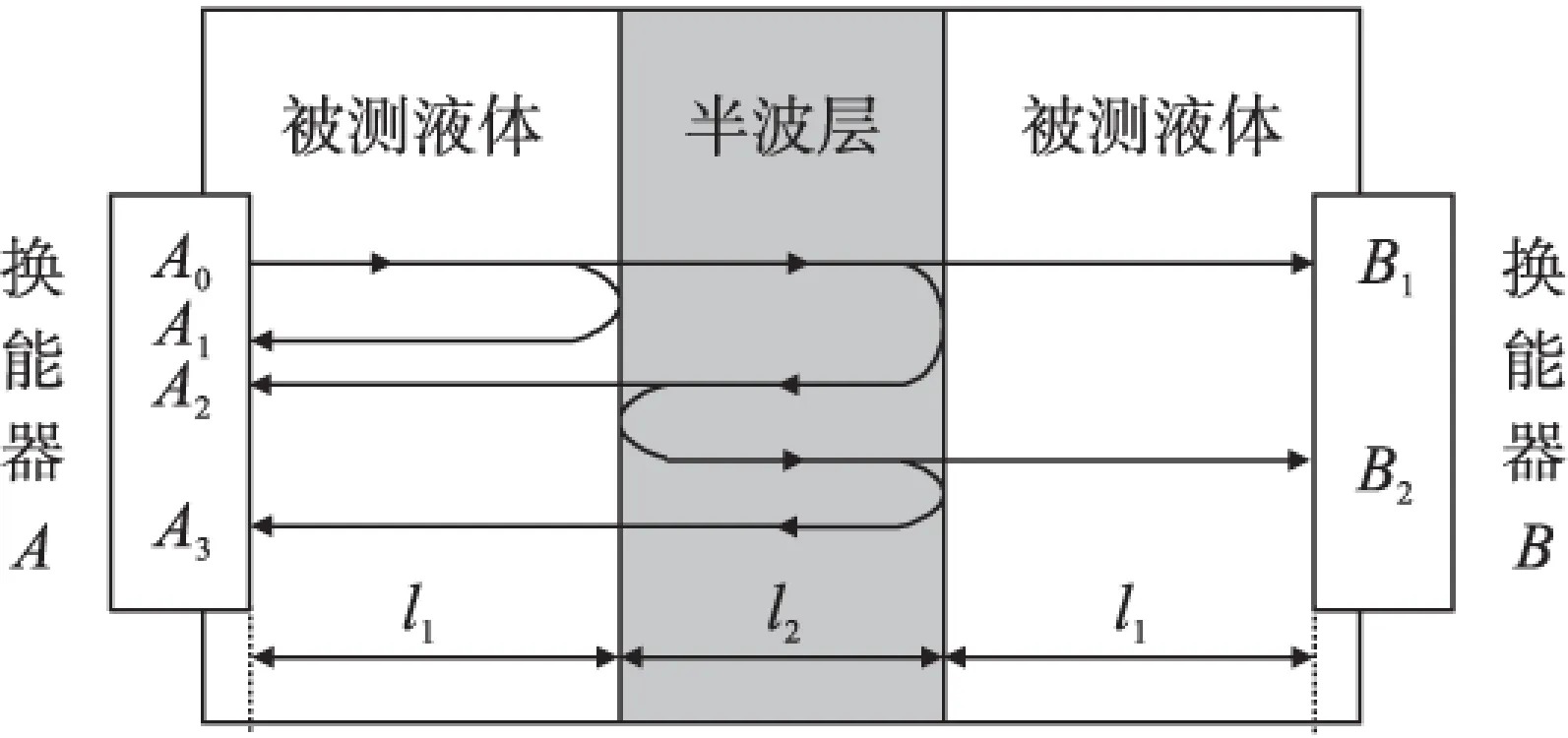
图4 简化后的半波层反射模型
1 测量原理与理论分析
简化后的半波层反射模型如图4所示,换能器A工作在脉冲回波模式,在测量结构的另一端换能器B工作在接收模式。每个换能器都会考虑n重回波的幅度。图中A0为入射波幅值,Ai和Bi为i次反射后换能器A和换能器B接收到的信号幅值,l1表示换能器到半波层的距离,l2为半波层厚度。
1.1 回波幅度表达式
在图3所示的模型中,不仅需要计算换能器A作为发射换能器时换能器A和B的回波信号,同时也需要计算换能器B作为发射换能器时,换能器A和B的回波信号。由于如图4所示的简化模型采用对称布局,因此换能器A作为发射端和换能器B作为发射端时工作状态完全一致,所以简化模型中仅需要计算换能器A作为发射端时换能器A和B的回波信号,比文献[9]中的方法减少了一半的计算量。
设超声波在被测液体和半波层中的衰减系数分别为α1和α2,从被测液体到半波层的反射系数为R12、入射系数为T12,从半波层到被测液体的反射系数为R21、入射系数为T21,四者之间的关系如下[9]:
(4)
A0是换能器A作为发射换能器时,换能器A入射平面波的压力幅度,它是由换能器的发射灵敏度和换能器与被测液体之间的声耦合综合决定的,是未知量。定义灵敏度因子RA和RB为换能器A和B接收到的平面波电压幅度与平面波压力幅度的比值。
当换能器A作为发射换能器时,理论上换能器A得到的回波幅度可以表示为[9]:
A1=A0R12RAe-2α1l1
A2=A0T12R21T21RAe-2α1l1-2α2l2
A3=A0T12R21·(R21R21e-2α2l2)·T21RAe-2α1l1-2α2l2
⋮
An=A0T12R21·(R21R12e-2α2l2)n-2·T21RAe-2α1l1-2α2l2
(5)
相应地换能器B接收到的回波幅度可以表示为:
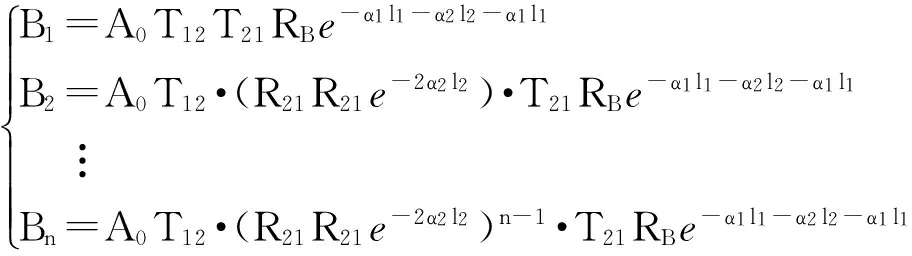
(6)
在图3的反射模型中,各回波幅度的推导过程需要计算从半波层到参考液体的反射系数R23和从参考液体到半波层的反射系数R32,图4所示的简化模型中用被测液体替换了图3模型中的参考液体,可以看做令R23=R21,R32=R12。因此简化模型中各回波幅度的推导过程比图3所示文献[9]的模型减少了变量,从而达到了简化推导过程的目的。
1.2 相对稳态幅度法
根据引言中提到的Hirnschrodt等人提出半波层反射模型可以知道,换能器的脉冲信号频率f选择正确使延迟材料厚度等于声波波长λ的n/2倍时,当驱动脉冲足够长,则延迟材料与参考液体两个交界面表面的回波会产生无损干涉,两个换能器接收的回波信号经过叠加后趋于稳态。
为了简化推导步骤,定义aA、qA、aB和qB如下:
(7)
将式(7)代入式(5)和式(6)可得[9]:
(8)
根据式(3)和式(8)可得:
(9)
当n→∞时,求和公式如下:
(10)
因此当n→∞时,换能器A和B的回波信号稳态幅度分别为:
(11)
则相对稳态幅度比K为:
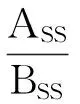
(12)
为简化计算,定义E为:
E=eα2l2-e-α2l2
(13)
根据式(12)和式(13)可得:
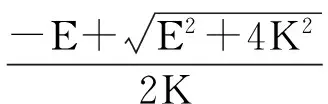
(14)
式中:E可根据超声波在半波层中的衰减系数α2和半波层厚度l2计算得到,因此当半波层材料选定后,E即为已知量。所以根据相对稳态幅度比K就可以求出反射系数R12。
从相对稳态幅度法的推导过程可以看出,与通常的声阻法模型相比,此方法仅考虑稳态时的幅值而不需要单独考虑各次回波的情况,降低了测量上的精度要求,可以减小测量上的误差。
2 实验论证
2.1 实验平台搭建
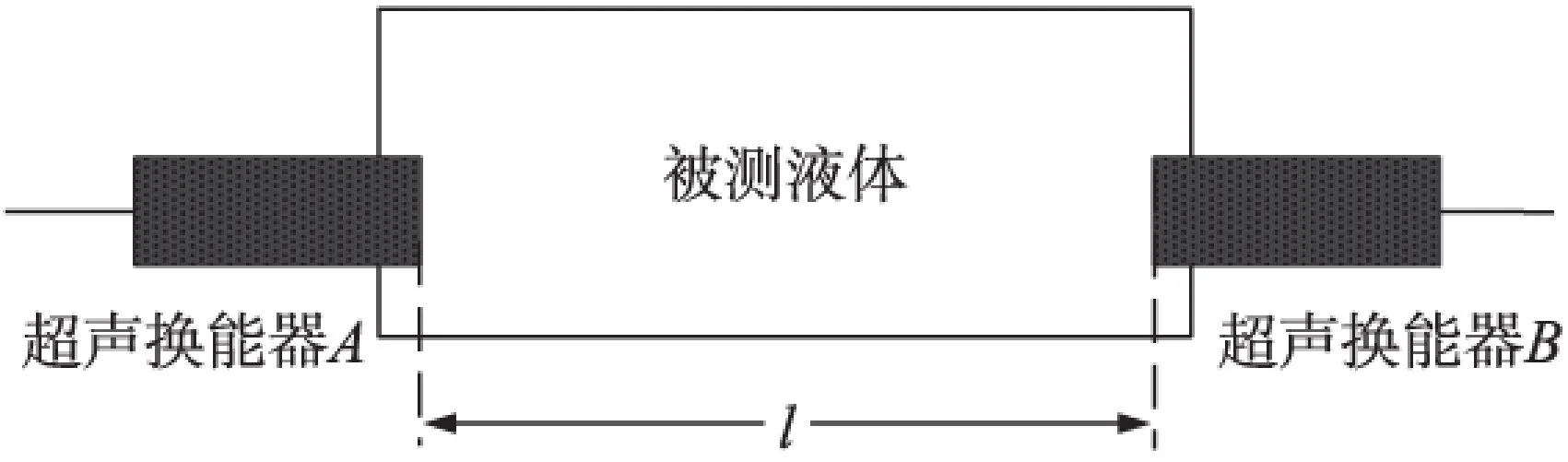
换能器的驱动信号是由任意波形发生器产生的周期可变频率可调的正弦波。换能器接收到的信号经放大后由数字化转换器采集,连接到PC机由LabVIEW和MATLAB软件进行数据处理。实验装置如图5所示。
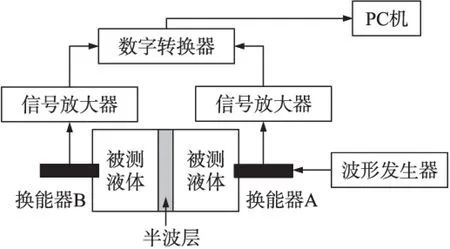
图5 实验装置结构图
半波层材料的选择要综合考虑其衰减系数和声阻抗。在此测试中,选择石英玻璃作为半波层材料,其优点在于:①熟知其声学特性,②高频下衰减系数较低,③有适当的声阻抗,使得被测液体和半波层之间有有效的声透射。
由于换能器的脉冲信号频率f要选择正确,使延迟材料厚度等于声波波长λ的n/2倍。波长λ=c/f,因此半波层厚度l2表达式如下:

(15)
式中:n为正整数。由于超声波传播过程中会发生衰减,所以半波层厚度不易过大。在实验室的环境下,为了保证延迟材料两个表面的回波发生无损干涉,以n=5为例进行实验。经过实验验证,取n=5能够满足要求。
实验中超声波探头的中心频率为1 MHz,查表可知超声波在石英玻璃中的声度为5 639 m/s,代入式(15)求得半波层厚度为14.097 5 mm。
由于超声波在传播过程中存在衰减,为了使回波信号幅值尽可能高,任意波形发生器的输出峰峰值幅度设为波形发生器最大输出10 V。
为了保证换能器A工作在脉冲回波模式,在1重回波信号到达换能器A之前,换能器A就要结束脉冲发送状态转换成回波接收状态[10],因此驱动信号周期不能过长。但延迟材料两个表面的回波发生无损干涉的条件之一是要求驱动脉冲足够长,经过多次试验,周期个数选为30个能够满足以上要求。
因此实验中半波层厚度为14.097 5 mm,换能器驱动信号的中心频率为1 MHz,峰峰值幅度为10 V,周期个数为30。
2.2 反射系数测量
利用图5所示装置测量水和半波层之间的反射系数R12。其回波信号如图6所示。
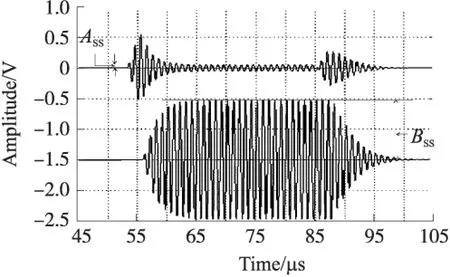
图6 被测液体为水时的回波信号
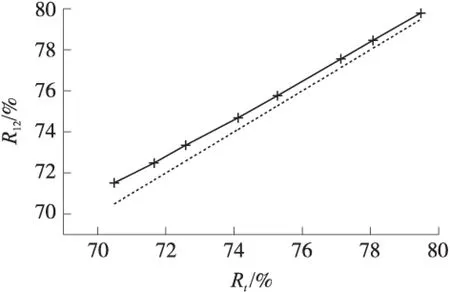
由图6可以看出,当时间t满足65 μs (16) 查阅文献可知频率为1 MHz时,石英玻璃的衰减系数α2=10.6×10-3dB/cm[11],厚度l2=14.097 5 mm,根据式(13)计算得到: E=eα2l2-e-α2l2=0.029 887 8 (17) 将K和E的值代入式(14)得: (18) 因此根据测量的幅值比可得,水与半波层之间的反射系数R12=79.785%。 2.3 测量结果及分析 反射系数理论值Rt计算步骤: ①测量被测液体密度ρ1。测量仪器为电子式液体密度计,型号为BHDM-YM08。 ②测量被测液体中声速c1。测量装置如图7所示,超声换能器A作为发射端,超声换能器B作为接收端[12]。用示波器同时测量超声换能器A的发射信号和超声换能器B的接收信号,利用示波器得到超声波从A到B的传播时间Δt,测得超声换能器A和B之间的距离l,则被测液体中声速c1=l/Δt。 图7 声速测量装置 ③根据式(1)求反射系数理论值Rt。已知石英玻璃密度ρ2=2.205 g/cm3,石英玻璃中超声波的声速c2=5 639 m/s[11],再将测量得到的被测液体密度ρ1和被测液体中声速c1代入式(1)即可求出被测液体的反射系数理论值Rt。 对不同浓度食盐水分别进行实验,得到的数据如表1实验结果所示,测量差值ΔR计算公式如下: ΔR=R12-Rt (19) 测量结果R12与理论值Rt的对比情况如图8所示,其中横坐标为反射系数的理论值Rt,纵坐标为测量值R12;虚线表示R12=Rt的直线,实线为实际测量值对应点的连线。 图8 R12与Rt的比较 由表1可以看出,测量差值ΔR≤0.011,且ΔR随反射系数的减小而增大。这是因为被测液体与半波层的声阻抗的差越小,回波的稳态幅度越不明显,幅值比测量误差越大,从而使反射系数的测量偏差也越大。文献[9]中测量差值ΔR≤0.02,通过本文所述的简化模型测量得到的测量差值ΔR≤0.011,比文献[9]小。且对比两种方法的R12与Rt比较图可以看出,本文的R12与Rt比较图中实际测量点的连线与直线R12=Rt的拟合度更好。 本文在半波层反射模型的基础上,对模型进行了化简,用被测液体替换参考液体,采取对称布局,同时利用相对稳态幅度法,简化了理论推导过程,也降低了测量上的困难,减小误差。 ①由于模型采用对称布局,因此换能器A作为发射端和换能器B作为发射端时工作过程完全一致。与未简化的半波层反射模型相比,简化模型中仅需计算换能器A作为发射端时换能器A和B的回波信号,比文献[9]的原半波层法减少了一半的计算量。 ②用被测液体替换原模型中的参考液体后,推导过程不需要考虑从半波层到参考液体的反射系数R23和从参考液体到半波层的反射系数R32,减少了变量,从而达到了简化推导过程的目的。 ③本文在简化的半波层反射模型中,采用相对稳态幅度法。在考虑超声波衰减情况时,稳态幅值比的推导过程中可以消去超声波在被测液体中的衰减系数α1,仅剩下半波层的衰减系数α2和厚度l2是已知量,与通常的反射系数测量方法相比,大大简化了幅值比的计算。 ④与通常的反射系数测量方法相比,相对稳态幅度法仅需要测量稳态时的幅值而不需要单独测量各次回波的情况。因此测量回波信号时,不需要过高的时间精度,降低了测量上的困难,也减小了测量上的误差。 从实验结果中可以看出,利用简化后的半波层反射模型测量出的差值ΔR,小于未简化的半波层反射模型测量出了差值,简化模型中R12与Rt比较图中实际测量点的连线与直线R12=Rt的拟合度比原模型好。 [1] 魏佳佳. 超声液体声学特性测量技术研究[D]. 华南理工大学,2014. [2] 陈玉喜,单秉昆. 一种新的声阻抗值测量方法[J]. 科技视界,2015(9):6-6. [3] 刘佳鑫. 基于声阻抗法的液体密度超声测量模型研究[D]. 大连理工大学,2013. [4] Fisher D P,Magori D P,Von J A. Ultrasonic Device for Measuring Specific Density of a Fluid:EP,EP0483491[P]. 1995. [5] 刘奎武,边巍. 超声波检测液态食品密度的研究与应用[J]. 机电技术,2013(3):121-122. [6] Puttmer A,Hauptmann P,Henning B. Ultrasonic Density Sensor for Liquids[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2000,47(1):85-92. [7] Hirnschrodt M,Lerch R.Resonance Anti-Reflection for ultrasonic density Raeas-Ure-Ment[C]//Ultrasonics Symposium,1999. Proceedings. 1999 IEEE,1999:517-520. [8] Hirnschrodt M,A V J,Vontz T. Ultrasonic Characterization of Liquids Using Resonance Antireflection[J]. Ultrasonics,2000,38(1-8):200-205. [9] Liu J X,Wang Z Q,Li G F. Acoustic Method for Obtaining the Pressure Reflection Coefficient Using a Half-Wave Layer.[J]. Ultrasonics,2011,51(3):359-368. [10] 胡志钢,尹钦,许姝菡. 压电陶瓷换能器收发系统幅频特性建模与分析验证[J]. 传感技术学报,2015,28(5):641-647. [11] 冯若. 超声手册[M]. 南京:南京大学出版社,1999,116. [12] 尹少英,刘轩,何小辉. 一种用于测量液体密度的超声波声速测定装置:CN203519148U[P]. 2014. 李晓佳(1995-),女,汉族,黑龙江省,硕士研究生,从事铅酸蓄电池组在线监测技术研究,lixiaojia1995@139.com; 李国锋(1968-),男,汉族,大连理工大学电气工程学院教授,博士生导师。主要研究方向包括电气设备智能检测与信息处理等,506893446@qq.com。 A Method for Measuring the Acoustic Reflection Coefficient of Liquid Density Measurement by Ultrasonic Wave LI Xiaojia1,LIU Jiaxin2,LI Guofeng1* (1.Information and Electrical Engineering,Dalian University of Technology,Dalian Liaoning 116024,China;2.Electric Power Science Research Institut,State Grid Liaoning Electric Power Company Limited,Shenyang 110006,China) Measurement of acoustic reflection coefficient is the key point when measuring the density of liquid by ultrasonic wave. This paper presents a method for measuring the acoustic reflection coefficient through the relative steady state amplitude based on the simplified model of half wave reflection. A thin solid as a half wave layer is arranged in the measured liquid,and two ultrasonic transducers are placed on both sides of the measured liquid,symmetrically. One transmitter works in pulse-echo mode,and the other works in receiver mode. By adjusting the frequency of signal to make the multiple reflection wave at the interface between the half wave layer and the liquid interfere to the greatest extent,the acoustic reflection coefficient between the liquid and the half wave layer is only related to the amplitude ratio of the two transducers in steady state. So the sound acoustic reflection coefficient can be obtained when the echo signal amplitude ratio of the transducer in steady state is measured.This method simplifies the process of theoretical derivation and reduces the accuracy of the measurement,by simplifying the original half wave reflection model,taking the symmetrical layout and using the method of relative steady state amplitude. At last,experiments are carried out to verify this method. ultrasonic sensor;acoustic reflection coefficient;half wave reflection method;relative steady state amplitude method;liquid density measurement 2016-12-30 修改日期:2017-02-16 TM930 A 1004-1699(2017)07-0985-06 C:7320 10.3969/j.issn.1004-1699.2017.07.002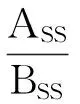
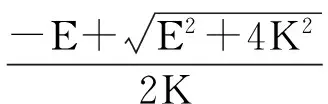

3 结束语


