低能电子在外层导电屏蔽的玻璃锥管中的传输∗

钱立冰 李鹏飞 靳博 靳定坤 宋光银 张琦 魏龙牛犇 万成亮 周春林 Arnold Milenko Müller Max Dobeli

宋张勇4) 杨治虎4) Reinhold Schuch5) 张红强1)†陈熙萌1)‡

1)(兰州大学核科学与技术学院,兰州 730000)

2)(中国核动力研究设计院,成都 610005)

3)(ETH Swiss Federal Institute of Technology,8092 Zurich,Switzerland)

4)(中国科学院近代物理研究所,兰州 730000)

5)(Physics Department,Stockholm University,S-106 91 Stockholm,Sweden)

低能电子在外层导电屏蔽的玻璃锥管中的传输∗

钱立冰1)李鹏飞1)靳博1)靳定坤1)宋光银1)张琦1)魏龙1)牛犇1)万成亮1)周春林2)Arnold Milenko Müller3)Max Dobeli3)

宋张勇4)杨治虎4)Reinhold Schuch5)张红强1)†陈熙萌1)‡

1)(兰州大学核科学与技术学院,兰州 730000)

2)(中国核动力研究设计院,成都 610005)

3)(ETH Swiss Federal Institute of Technology,8092 Zurich,Switzerland)

4)(中国科学院近代物理研究所,兰州 730000)

5)(Physics Department,Stockholm University,S-106 91 Stockholm,Sweden)

(2017年2月9日收到;2017年3月13日收到修改稿)

采用新的具有常数锥角的玻璃锥管,并对玻璃锥管进行了外表面导电屏蔽,通过对电子穿越玻璃锥管的二维角分布随时间演化的观测,研究了低能电子与玻璃管相互作用的机制.发现电子穿越完全放电的玻璃锥管时穿透率先下降后平稳,整个过程中角分布中心发生微小移动,但角分布的半高宽几乎保持不变.这与我们之前发表的工作(2016 Acta Phys.Sin.65 204103)不同,这是由于对玻璃锥管进行外表面导电屏蔽会阻止外界不确定的快速充放电的影响,并形成了新的稳定放电通道,有利于实现电子的稳定穿透.电子的穿透率随倾角呈类似矩形的分布,透射电子的角分布中心伴随倾角的变化而移动,其穿透所容许的倾角与几何穿透一致.

电子,导电效应,玻璃管

1 引 言

近些年来,荷电粒子与绝缘体纳米微孔相互作用的研究成为离子束研究领域内的热点.这是由于在纳米微孔的倾角远大于由纳米微孔纵横比决定的几何张角处观察到了穿透离子,这些穿透离子的电荷态和能量与入射离子相同,这种现象被称为导向效应[1−4].导向效应最早是采用3 keV的Ne7+穿透聚对苯二甲酸类塑料(polyethylene terephthalate,PET)膜上的纳米微孔后被发现的[1].导向效应是初始离子与微孔的相互作用使在孔管内壁自组织形成电荷斑,这种电荷斑沿着微孔轴向按序列分布[4],从而形成阻止入射离子与表面近碰撞的电场,后续粒子沿着玻璃管的轴向出射.绝缘毛细管的导向效应为新的带电粒子及离子束光学方法的产生带来可能.国内外已有许多研究组开展了这方面的工作,通过用各种入射离子束(高电荷态离子、单电荷态离子、分子离子、电子、µ子、正电子和负离子)来打各种各样的绝缘纳米毛细管(PET,SiO2,Al2O3,PC和云母)、玻璃毛细管(出口处为微米到纳米量级)以及绝缘管子(聚四氟乙烯和玻璃)来研究导向效应[5−20].更详细的关于这个领域的工作可参阅综述文献[21,22].

已有的关于导向效应的研究大多数集中在高电荷态离子与纳米微孔的作用,其结果清晰,物理机制也研究得比较清楚明确,但是目前为止,关于电子的导向效应的物理机制存在争论,就连涉及导向效应的最基本的机制,即入射粒子沉积负电荷产生一个有利于后续粒子传输的负电场也处于争论中.2007年,美国的研究小组采用低能电子穿越PET绝缘纳米毛细管[5],这是关于电子与纳米微孔的导向效应的最早的研究之一.他们通过穿透电子能谱发现一部分穿透电子有明显的能量损失,并且这种能量损失随着毛细管倾角的变大而增加.这与在高电荷态离子与玻璃毛细管相互作用的实验中观察到的绝大多数穿透粒子未发生能量损失和电荷交换有很大的不同.随后的理论模拟结果显示[14],电子在这个纳米微孔中的沉积电荷和电场与离子完全不同,没有在入口处产生明确的负电荷斑造成的负电场.但是该研究小组坚持在实验中寻找与理论模拟结果不同的证据来证明有负电荷斑造成的负电场[7−9].同时,塞尔维亚的Milosavljević等[6]采用Al2O3微孔膜,发现了电子穿透率随时间下降,但是他们测量的角分布特征又与正离子导向效应相似.这种在电子导向效应研究中的前后矛盾和不一致的结果一直困绕着这个领域内的研究者.之前的电子导向效应的实验,尤其是涉及动力学过程的实验是用一维静电能谱仪来测量穿透电子的能谱和角分布[5,6].由于一维静电能谱仪在入口处有一个狭缝,在每一步测量中只能容许穿透电子角分布的一部分被测量到,而且探测器的角度移动是机械移动,因此无法对时间依赖的穿透电子的角分布在秒量级的快速变化进行跟踪测量,进而使得对于电子是否沉积负电荷而发生类似正离子的导向效应的观测和理解是有困难的.

为了克服这个缺点,我们利用微通道板(MCP)与荧光板以及电荷耦合器相机(charge coupled device,CCD)组成的二维成像系统[23,24]直接获得穿透电子全角分布的时间演化和动力学过程,研究穿透电子角分布在快速充放电过程中的变化[6].发现低能电子在玻璃直管和锥管中存在多次快速充放电的振荡行为:每次充放电过程持续几秒,穿透强度先增大后减小,整个过程伴随着角分布中心的移动,以及角分布宽度的先增大后减小,整个振荡显示了电子穿越玻璃锥管时极不稳定的穿透行为.这与高电荷态离子比较稳定的穿透率和规则变化的角分布有着很大的区别.同时我们的研究也证明,对电子在绝缘毛细管中导向效应的动力学过程及机理的研究必须考虑穿透角分布的移动和演化问题.

本文,我们对玻璃锥管进行了外表面导电屏蔽,从而阻止了外界不确定的快速充放电的影响,并形成了新的稳定放电通道,从而获得了1.5 keV的低能电子束通过高硼硅玻璃锥管的稳定穿透.研究发现电子穿透率随倾角呈类似矩形的分布,在穿透率平稳区域的倾角改变值与毛细管的几何张角相一致.当倾角大于几何张角时,穿透率快速减小.穿透电子角分布中心移动的角度小于倾角改变的角度.当倾角在几何张角容许范围内时角分布的宽度几乎保持不变,但在大于几何张角的倾角下穿透电子的角分布宽度也快速减小.对1.5 keV电子穿越完全放电后的玻璃锥管在−0.6◦倾角下的二维角分布的时间演化测量发现,电子穿透率随时间下降到一个值后保持不变,穿透电子角分布中心发生微小移动,整个角分布的宽度基本保持不变.

2 实验装置

实验装置如图1所示.由电子枪产生能量为1.5 keV的低能电子束,通过弧形偏转板做90◦偏转,经过水平和竖直偏转板以及管式电透镜的传输后,通过两个四级狭缝以及螺线圈准直聚焦[25],成为束斑大小为0.5 mm×0.5 mm、强度为21.3 fA/mm2的电子束.为减少地球磁场对电子束流传输和探测的影响,我们对整个束流传输系统和探测系统进行了地球磁屏蔽.

穿越的电子轰击在MCP上,经多次倍增后轰击在P43型荧光材料构成的荧光板上产生绿色荧光,荧光经45◦全反射镜反射透过真空隔离石英窗(对绿光的透射率接近100%)进入CCD相机成像.实验所用的CCD相机量子效率为75%,610万有效像素,芯片大小为1英寸.CCD相机曝光时间范围1 ms—160 min,增益范围15—42 dB,测量时CCD的曝光时间为500 ms,增益为25 dB.

实验中锥形玻璃管在瑞士苏黎士联邦理工学院制备,其入口内径为1.2 mm,出口直径为225µm,其中直管端长为23.3 mm,锥形部分长为35.1 mm,锥形部分的张角即锥角δ=0.8◦为常数,实验中玻璃管外表面除从出口开始1.1 mm长的部分绝缘外,其他位置都涂有导电层以防止不稳定的充放电现象[25].在玻璃管入口处增加了一狭缝,孔径为0.3 mm,如图2所示.这是为了防止电子打在入口表面充电,从而影响后续的电子进入玻璃管内,同时这样做会使得玻璃锥管入口尺寸比束流尺寸小.玻璃管入口(0.3 mm)与出口(225µm)之间的发散角β为0.26◦.

玻璃锥管安装在一个5维调角器上,可以在三个方向(前后、左右、上下)独立移动并沿着水平面(倾角)和竖直平面(仰角)内独立转动.玻璃锥管入口对应倾角和仰角角度旋转的中心,标记玻璃锥管倾角α为玻璃管中心轴与束流在水平方向的夹角,定义ϕ和θ为水平方向和竖直方向的探测角度(如图1所示).探测系统可以在水平面内以靶室中心竖直轴为轴转动.

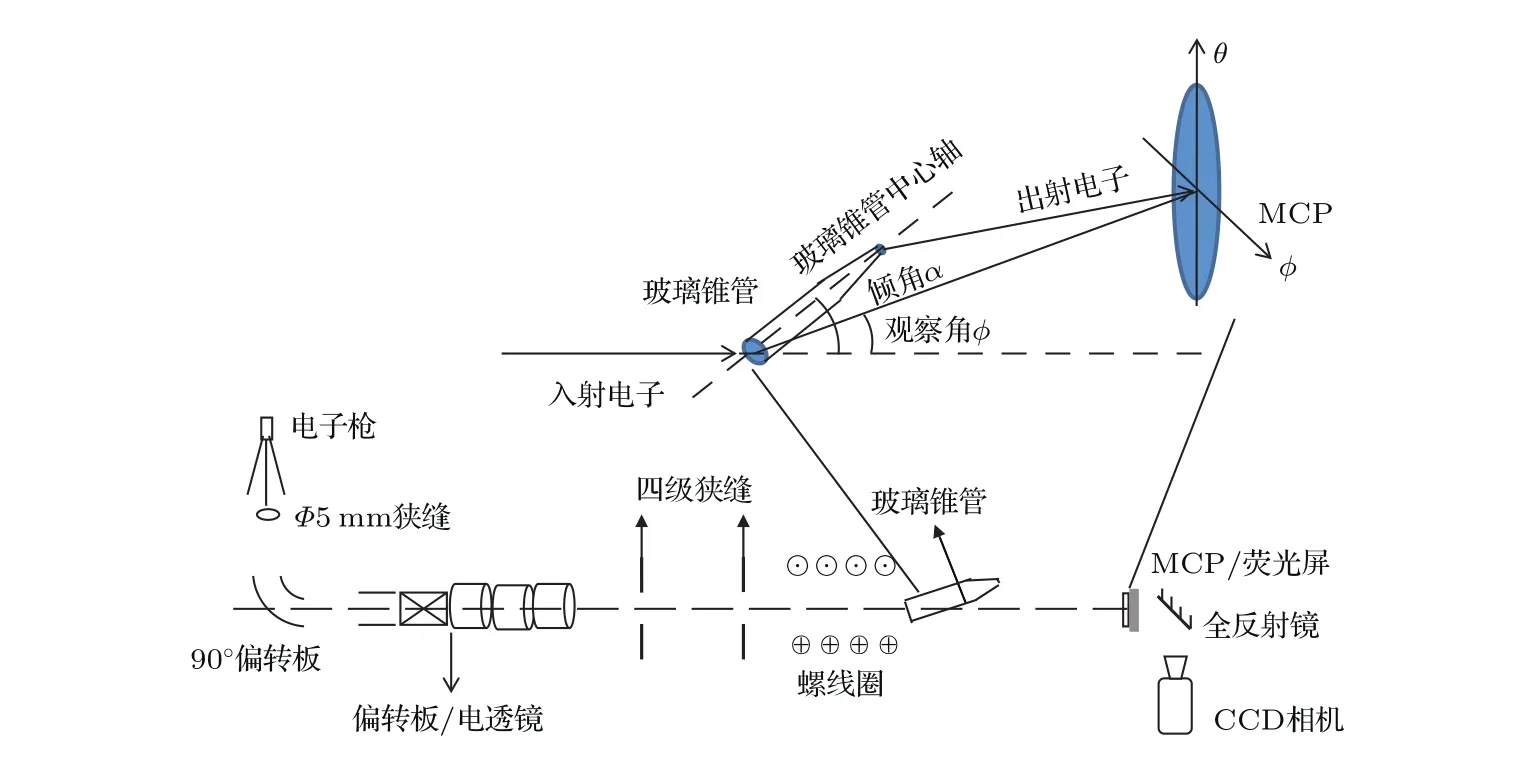
图1 (网刊彩色)实验装置和探测角几何示意图Fig.1.(color online)Schematic diagram of experimental setup and the geometry of the observation angles.

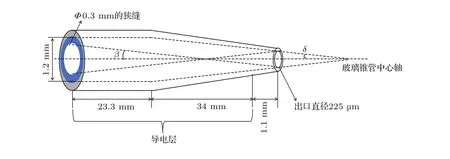
图2 (网刊彩色)玻璃毛细锥管示意图Fig.2.(color online)Schematic diagram of the conical glass capillaries.

我们在二维探测器上获取的初始电子束的角分布如图3所示,其中曲线a和b分别是束斑在ϕ和θ方向的投影.由束斑的大小(水平方向尺寸和竖直方向尺寸都为0.5mm)可以得出对应以靶室为中心的角发散度为0.35◦,电子束的束流角发散则不大于这个值.

图3 (网刊彩色)1.5 keV入射电子束的二维角分布图像,其中曲线a,b分别为二维角分布在ϕ方向和θ方向的投影,红色实线为高斯拟合曲线Fig.3.(color online)The incident beam(1.5 keV electrons)image and corresponding projections on the ϕ plane(curve a)and θ plane(curve b).The solid lines in the projections are Gaussian fi t curves.

3 实验结果与讨论

3.1 不同入射倾角下电子穿越玻璃锥管的稳态角分布

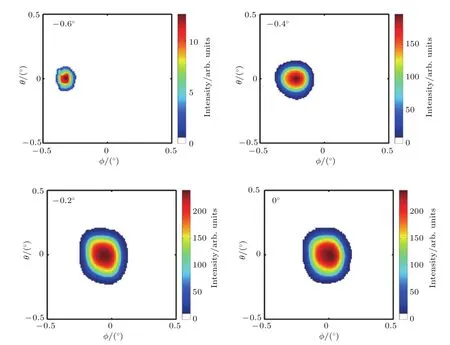
图4 (网刊彩色)不同倾角下1.5 keV电子穿越玻璃锥管的二维角分布Fig.4.(color online)The two dimensional angle distributions of 1.5 keV electrons transmitted through the conical glass capillary for various tilt angle(α angle).

我们仔细地调节了电子穿透玻璃锥管时其倾角和仰角的变化,以寻找最大穿透率的角度,确定了0◦位置(调角器倾角最小步长为0.0025◦,由精密步进马达控制).为了精细地测量穿透电子角分布随倾角的变化,设倾角移动步长为0.05◦.图4显示了部分不同倾角α下电子穿越玻璃锥管的稳态角分布,每幅图像左侧标示出所对应的倾角.为了清楚地研究角分布的变化情况,我们将穿透电子二维角分布在ϕ方向投影,如图5所示,图中给出了实验测量的出射电子角分布半高宽.当α=−0.6◦时,穿透角分布中心为−0.35◦,随着倾角的移动,穿透电子角分布中心也移动,但与入射倾角不呈现离子那样的一对一的关系[1].图6为穿透电子角分布的宽度随倾角的变化.在倾角为0◦附近,我们测量到的角分布半高宽为0.23◦左右,这与锥管的几何张角非常符合(出口与入口形成的准直角为0.26◦).电子穿越玻璃锥管的出射电子透射率随入射倾角呈矩形分布,如图7所示.可以看出在−0.2◦到0.2◦之间透射率几乎没有变化.

3.2 电子穿越玻璃锥管随入射电荷(时间)的演化

为研究电子与玻璃锥管相互作用中的充放电机制,我们采用1.5 keV电子,测量其穿越完全放电后的玻璃锥管在−0.6◦倾角下的二维角分布随时间的演化.图8(a)是穿透电子的二维角分布,其中ϕ和θ分别为水平方向和竖直方向的探测角度(如图1所示),由图可见,开始时出现大亮斑,随后逐渐变暗,最后保持不变.为了研究角分布的变化情况,我们将二维角分布在ϕ方向投影,图8(b)是充放电过程中ϕ方向角分布随时间的演化,其中红色实线为高斯拟合曲线.可以看出对于玻璃锥管,穿透电子的强度峰值没发生大角度的移动.为了便于定量比较这种角分布的时间演化,我们在图9中给出了充放电过程中ϕ方向角分布中心位置随时间的演化,整个过程中穿透角分布中心有所移动,穿透角分布中心最先出现在−0.35◦位置,随后移动并稳定在−0.33◦.整个角分布的宽度基本保持在0.1◦左右.图10所示为电子穿越玻璃锥管的透射率随时间的演化,透射率先减小后达到一个平稳值.图中横坐标下部以时间标记,横坐标上部表示与时间相对应的电荷累积量.

图5 (网刊彩色)不同倾角下穿透电子二维角分布在ϕ方向的投影(为了更好地显示角分布,α=−0.6◦时的角分布强度在图中被放大了10倍)Fig.5.(color online)The transmitted angular distributions projected onto the ϕ plane for various tilt angle(α angle),and the intensity is ampli fi ed up to 10 times at tile angle−0.6◦.

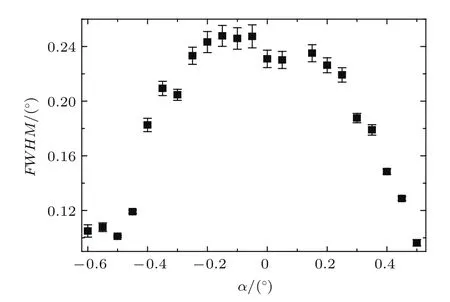
图6 ϕ方向上穿透电子角分布半高宽随倾角的变化Fig.6.The full width at half maximum of the transmitted angular distributions in the ϕ plane for various tilt angle(α angle).

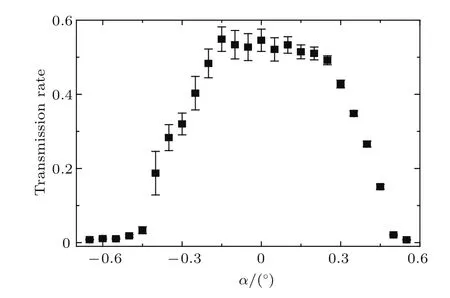
图7 1.5 keV电子穿越玻璃锥管时透射率随倾角的变化Fig.7. The transmission rate of 1.5 keV electrons through the conical glass capillaries as a function of tilt angle(α angle).

3.3 结果讨论

我们观测到了电子穿透玻璃锥管之后的稳定角分布,意味着电子与玻璃锥管相互作用时的充放电过程达到了一个平衡状态,这与之前观察到的快速充放电现象[25]不同,差别在于我们对玻璃锥管进行了外表面导电屏蔽,从而阻止了外界不确定的快速充放电影响并形成了新的稳定放电通道,这种构型有利于实现电子的稳定穿透.这对于后续采用玻璃锥管等其他绝缘体材料作为电子束流光学传输元件有着极大的启发意义.

玻璃锥管几何张角β=0.26◦束流发散度σ=0.35◦时,几何穿透情况下容许的穿透角度为这与实验测量的结果(0.4◦)相符合.电子在玻璃锥管中的最大穿透率为0.55,也与几何穿透率0.56相符合.同样,电子穿透角分布的中心没有像离子那样随倾角一对一移动,而是在几何穿透角容许的范围内移动,玻璃锥管如同几何准直,只有被容许的特定发散角的入射电子才能穿越,实验中在大于几何张角容许的倾角下未观察到明显的出射电子.

对于完全放电的玻璃锥管动力学过程的实验观察发现,穿透电子角分布的中心移动方向和穿透率随入射电荷(时间)的变化等穿透特性显示电子穿越绝缘体玻璃锥管的传输机制与高电荷态离子有很大不同:对于电子入射,由于玻璃的二次电子发射系数在实验能量1.5 keV下大于1,这会使得直接暴露到电子束的玻璃锥管的内表面被充了正电,从而形成了阻止后续入射电子穿透的正电场,如图11所示.这将使得与束流直接接触的带正电的内表面偏转,后续电子向小观察角即ϕ=0◦方向变化,这与实验中观察到的微小移动方向一致(从−0.35◦到−0.33◦),这个电场也将导致穿越电子被偏转到孔壁上而无法穿越,从而导致电子穿透率随时间下降,而不是像离子导向效应中那样随时间上升.

图8 (网刊彩色)(a)1.5 keV电子穿越倾角为−0.6◦的玻璃锥管时二维角分布随时间的演化;(b)对应的二维角分布在ϕ方向的投影随时间的演化Fig.8.(color online)(a)The two dimensional angle distributions of 1.5 keV electrons at tile angle−0.6◦transmitted through the conical glass capillary for various time;(b)the transmitted angular distributions projected onto the ϕ plane for various time.

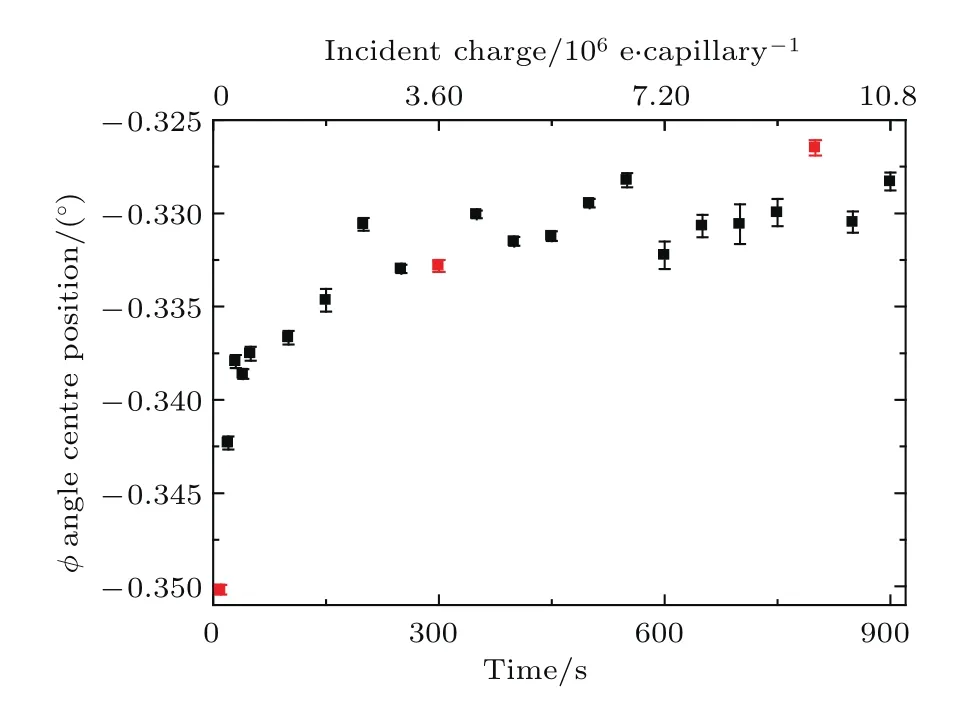
图9 (网刊彩色)1.5 keV电子穿越倾角为−0.6◦的玻璃锥管时出射电子ϕ方向角分布中心位置随时间的变化,其中,横坐标下部以时间标记,横坐标上部表示与时间相对应的电荷累积量(e/capillary),红色的点对应图8所呈现的二维穿透电子角分布Fig.9.(color online)The center position of the transmitted angular distributions of 1.5 keV electrons in the ϕplane for various time at tile angle −0.6◦.In the lower of the abscissa,the unit is time,and the upper of abscissa shows the accumulation of charge(e/capillary),corresponding to time.

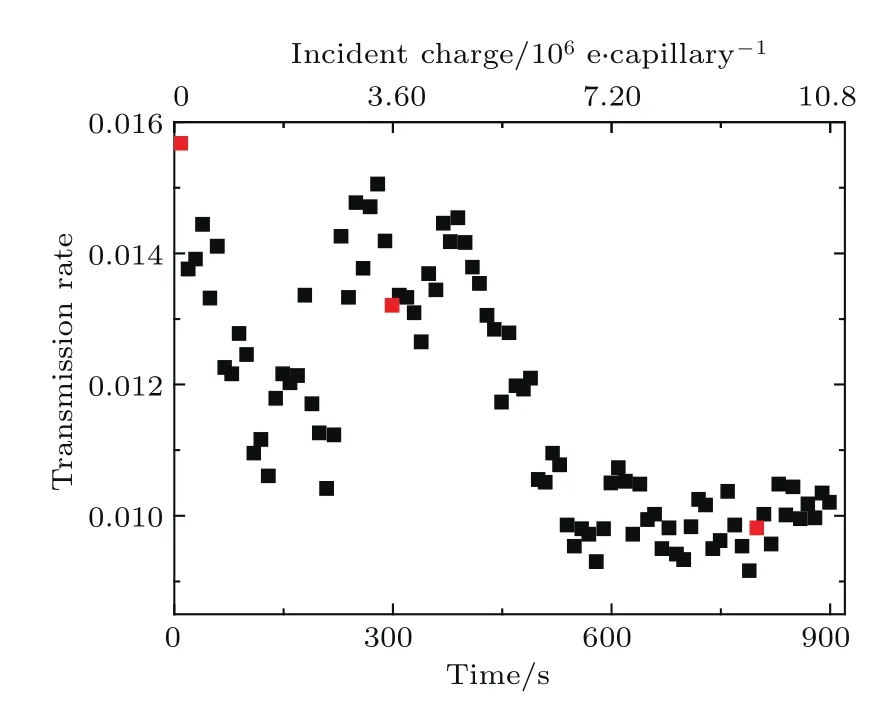
图10 (网刊彩色)1.5 keV电子穿越倾角为−0.6◦的玻璃锥管时透射强度随时间的演化,其中,横坐标下部以时间标记,横坐标上部表示与时间相对应的电荷累积量(e/capillary),红色的点对应图8所呈现的二维穿透电子角分布Fig.10.(color online)The transmission rate of 1.5 keV electrons through glass capillaries as a function of time at tile angle −0.6◦.In the lower of the abscissa,the unit is time,and the upper of abscissa shows the accumulation of charge(e/capillary),corresponding to time.

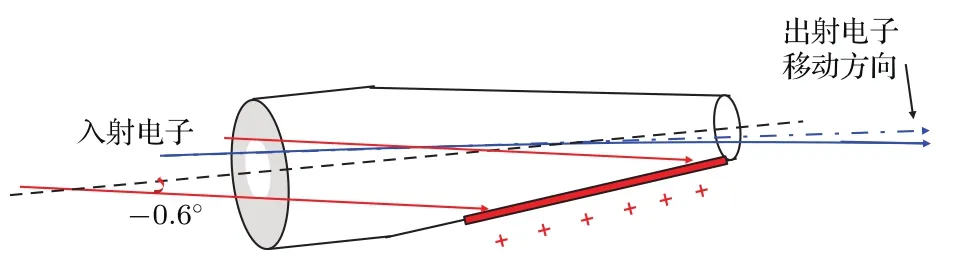
图11 (网刊彩色)1.5 keV电子穿越倾角为−0.6◦的玻璃锥管时两者相互作用过程示意图Fig.11.(color online)Scenario of 1.5 keV electrons transmitted through the glass capillary at the tile angle of−0.6◦.

4 结 论

我们通过实验测量了低能电子穿透外层导电屏蔽的玻璃锥管随时间和倾角变化的全角分布二维图像,发现低能电子在锥管中的一种直接穿透现象.电子穿越不同倾角的玻璃管时,出射电子的穿透率呈矩形,穿透率和角分布宽度在几何张角容许范围内是一个不变值,穿透角分布中心随倾角发生微小移动.电子穿越完全放电的玻璃锥管时穿透率先下降后平稳,整个过程中角分布中心发生微小移动.电子穿越玻璃锥管只在几何容许的角度范围内观察到出射电子,这与高电荷态离子在大于几何容许的角度范围内观察到出射离子的过程有很大不同.带负电的电子与带正电的离子与绝缘体材料的相互作用过程的电荷沉积方式不同,电子穿越时没有形成有利于电子传输的负电荷斑,而正电离子却能形成正的电荷斑,利于后续入射离子传输而形成导向效应.

[1]Stolterfoht N,Bremer J H,Ho ff mann V,Hellhammer R,Fink D,Petrov A,Sulik B 2002 Phys.Rev.Lett.88 133201

[2]Stolterfoht N,Hellhammer R,Bundesmann J,Fink D,Kanai Y,Hoshino M,Kambara T,Ikeda T,Yamazaki Y P 2007 Phys.Rev.A 76 022712

[3]Schiessl K,Pal fi nger W,Tőkési K,Nowotny H,Lemell C,Burgdőrfer J 2005 Phys.Rev.A 72 062902

[4]Skog P,Zhang H Q,Schuch R 2008 Phys.Rev.Lett.101 223202

[5]Das S,Dassanayake B S,Winkworth M,Baran J L,Stolterfoht N,Tanis J A 2007 Phys.Rev.A 76 042716

[6]Milosavljević A R,Víkor G,Pešić Z D,Kolarž P, Šević D,Marinković B P,Máté fi-Temp fl i S,Máté fi-Temp fl i M,Piraux L 2007 Phys.Rev.A 75 030901

[7]Keerthisinghe D,Dassanayake B S,Wickramarachchi S J,Stolterfoht N,Tanis J A 2013 Nucl.Instrum.Meth.Phys.Res.B 317 105

[8]Wickramarachchi S J,Dassanayake B S,Keerthisinghe D,Ikeda T,Tanis J A 2013 Phys.Scr.T156 014057

[9]Wickramarachchi S J,Ikeda T,Dassanayake B S,Keerthisinghe D,Tanis J A 2016 Phys.Rev.A 94 022701

[10]Kanai Y,Hoshino M,Kambara T,Ikeda T,Hellhammer R,Stolterfoht N,Yamazaki Y 2009 Phys.Rev.A 79 012711

[11]Stolterfoht N,Hellhammer R,Fink D,Sulik B,Juhász Z,Bodewits E,Dang H M,Hoeks R 2009 Phys.Rev.A 79 022901

[12]Sahana M B,Skog P,Vikor G,Rajendra Kumar R T,Schuch R 2006 Phys.Rev.A 73 040901

[13]Krause H F,Vane C R,Meyer F W 2007 Phys.Rev.A 75 042901

[14]Skog P,Soroka I L,Johansson A,Schuch R 2007 Nucl.Instrum.Meth.Phys.Res.Sect.B 258 145

[15]Sun G Z,Chen X M,Wang J,Chen Y F,Xu J K,Zhou C L,Shao J X,Cui Y,Ding B W,Yin Y Z,Wang X A,Lou F J,Lü X Y,Qiu X Y,Jia J J,Chen L,Xi F Y,Chen Z C,Li L T,Liu Z Y 2009 Phys.Rev.A 79 052902

[16]Schiessl K,Tőkési K,Solleder B,Lemell C,Burgdőrfer J 2009 Phys.Rev.Lett.102 163201

[17]Zhang H Q,Akram N,Skog P,Soroka I L,Trautmann C,Schuch R 2012 Phys.Rev.Lett.108 193202

[18]Zhou W,Niu S T,Yan X W,Bai X F,Han C Z,Zhang M X,Zhou L H,Yang A X,Pan P,Shao J X,Chen X M 2016 Acta Phys.Sin.65 103401(in Chinese)[周旺,牛书通,闫学文,白雄飞,韩承志,张鹛枭,周利华,杨爱香,潘鹏,邵剑雄,陈熙萌2016物理学报65 103401]

[19]Wang W,Chen J,Yu D Y,Wu Y H,Zhang M W,Cai X H 2011 High Power Laser and Particle Beams 23 1065(in Chinese)[王伟,陈婧,于得洋,武晔虹,张明武,蔡晓红2011强激光与粒子束23 1065]

[20]Chen Y F,Chen X M,Lou F J,Xu J Z,Shao J X,Sun G Z,Wang J,Xi F Y,Yin Y Z,Wang X A,Xu J K,Cui Y,Ding B W 2010 Acta Phys.Sin.59 222(in Chinese)[陈益峰,陈熙萌,娄凤君,徐进章,邵剑雄,孙光智,王俊,席发元,尹永智,王兴安,徐俊奎,崔莹,丁宝卫 2010物理学报59 222]

[21]Lemell C,Burgdörfer J,Aumayr F 2013 Prog.Surf.Sci.88 237

[22]Stolterfoht N,Yasunori Y 2016 Phys.Rep.629 1

[23]ALPHA Collaboration,Andresen G B,Bertsche W,Bowe P D,Bray C C,Butler E,Cesar C L,Chapman S,Charlton M,Fajans J,Fujiwara M C,Gill D R,Hangst J S,Hardy W N,Hayano R S,Hayden M E,Humphries A J,Hydomako R,Jørgensen L V,Kerrigan S,Kurchaninov L,Lambo R,Madsen N,Nolan P,Olchanski K,Olin A,Povilus A P,Pusa P,Sarid E,Seif S,Silveira D M,Storey J W,Thompson R I,Vander D P,Yamazaki Y 2009 Rev.Sci.Instrum.80 123701

[24]Varialee V 2015 Phys.Procedia 66 242

[25]Wan C L,Li P F,Qian L B,Jin B,Song G Y,Gao Z M,Zhou L H,Zhang Q,Song Z Y,Yang Z H,Shao J X,Cui Y,Reinhold S,Zhang H Q,Chen X M 2016 Acta Phys.Sin.65 204103(in Chinese)[万城亮,李鹏飞,钱立冰,靳博,宋光银,高志民,周利华,张琦,宋张勇,杨治虎,邵剑雄,崔莹,Reinhold Schuch,张红强,陈熙萌 2016物理学报65 204103]

PACS:41.85.Ja,41.85.Lc,41.75.FrDOI:10.7498/aps.66.124101

Transmission of electrons through the conical glass capillary with the grounded conducting outer surface∗

Qian Li-Bing1)Li Peng-Fei1)Jin Bo1)Jin Ding-Kun1)Song Guang-Yin1)Zhang Qi1)Wei Long1)Niu Ben1)Wan Cheng-Liang1)Zhou Chun-Lin2)Arnold Milenko Müller3)Max Dobeli3)Song Zhang-Yong4)Yang Zhi-Hu4)Reinhold Schuch5)Zhang Hong-Qiang1)†Chen Xi-Meng1)‡

1)(School of Nuclear Science and Technology,Lanzhou University,Lanzhou 730000,China)
2)(Nuclear Power Institute of China,Chengdu 610005,China)
3)(ETH Swiss Federal Institute of Technology,8092 Zurich,Switzerland)
4)(Institute of Modern Physics,Chinese Academy of Science,Lanzhou 730000,China)
5)(Physics Department,Stockholm University,S-106 91 Stockholm,Sweden)

9 February 2017;revised manuscript

13 March 2017)

The transmission of 1.5 keV-electrons through a conical glass capillary is reported.This study aims to understand the so-called guiding e ff ect for the negatively charged particles(e.g.electrons).The guiding mechanism is understood quite well with positively charged particles in particular highly charged ions,but not clear with electrons,i.e.,even the basic scheme mediated by the existence of negative charge patches to guide the electrons is still somewhat controversial.

The study of the charging-up dynamics causing the electrons transport inside the capillary will shed light on this issue.In order to perform this,a data acquisition system has been setup to follow the time evolution of the twodimensional angular distribution of the transmitted electrons.The electrons are detected by the multi-channel plate(MCP)detector with a phosphor screen.The image from the phosphor screen is recorded by a charge-coupled device camera.The timing signals for the detected events are extracted from the back stack of the MCP detector and recorded by the data acquisition system,synchronized with the acquired images.The electron beam has a size of 0.5 mm×0.5 mm and a divergence of less than 0.35◦.The inner diameter of the straight part of the capillary is 1.2 mm and the exit diameter is 225µm.A small conducting aperture of 0.3 mm in diameter is placed at the entrance of the capillary.Two-dimensional angular distribution of the transmitted electrons through conical glass capillary and its time evolution are measured.The results show that the transmission rate decreases and reaches to a constant value for the completely discharged glass capillary with time going by.The centroid of the angular distribution moves to an asymptotic value while the width remains unchanged.These transmission characteristics are di ff erent from those indicated in our previous work(2016 Acta Phys.Sin.65 204103).The di ff erence originates from the di ff erent manipulations of the capillary outer surface.A conducting layer is coated on the outer surface of the capillary and grounded in this work.This isolates various discharge/charge channels and forms a new stable discharge channel.The transmission rate as a function of the tilt angle shows that the allowed transmission occurs at the tilt angle limited by the geometrical factors,i.e.,the geometrical opening angle given by the aspect ratio as well as the beam divergence.The transmission characteristics suggest that most likely there are formed no negative patches to facilitate the electron transmission through the glass capillary at this selected beam energy.It is di ff erent from that of highly charged ions,where the formation of the charge patches prohibits the close collisions between the following ions and guides them out of the capillary.

electron,guiding e ff ect,glass capillaries

10.7498/aps.66.124101

∗国家自然科学基金(批准号:11475075)资助的课题.

†通信作者.E-mail:zhanghq@lzu.edu.cn

‡通信作者.E-mail:chenxm@lzu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11475075).

†Corresponding author.E-mail:zhanghq@lzu.edu.cn

‡Corresponding author.E-mail:chenxm@lzu.edu.cn