东方超环(EAST)装置中等离子体边界锂杂质的碰撞-辐射模型∗
2017-08-07章太阳陈冉
章太阳 陈冉
1)(中国科学技术大学核科学技术学院,合肥 230022)
2)(中国科学院合肥物质科学研究院等离子体物理研究所,合肥 230031)
东方超环(EAST)装置中等离子体边界锂杂质的碰撞-辐射模型∗
章太阳1)陈冉2)†
1)(中国科学技术大学核科学技术学院,合肥 230022)
2)(中国科学院合肥物质科学研究院等离子体物理研究所,合肥 230031)
(2017年1月4日收到;2017年4月2日收到修改稿)
在东方超环(EAST)装置中,由于大量锂化壁处理的使用,切向可见光摄像机拍摄到等离子体边界通常存在一条由锂(Li)杂质形成的绿色发光带.本文基于EAST边界等离子体参数条件,基于碰撞-辐射模型给出由已知边界等离子体状态推算Li绿光光强的空间分布的具体方法,并针对简化后的一维径向分布问题,收集、处理OPEN-ADAS数据库的数据,采用软件Mathematica 10.4.1编写相应的数值计算程序,分别输入EAST工作于低约束(L)与高约束(H)模时获得的两组边界电子温度、密度分布数据,给出并分析比较了利用该模型的计算结果.此项工作对于未来建立通过测量及反演边界锂杂质特征谱线强度的空间分布来重构边界等离子体状态的全新技术和研究存在三维磁场扰动条件下的边界等离子体行为均具有重要的理论参考价值.
等离子体杂质,托卡马克,碰撞-辐射模型
1 引 言
切向可见光高速相机系统是用于磁约束聚变装置的常规探测系统.在现有的托卡马克装置中,其通过观测和拍摄记录等离子体在可见光波段的发光过程,进而可以针对放电状态和等离子体位型等关键信息实现定性评估.此外,在未来的包括国际热核聚变实验堆(ITER)[1]等下一代聚变堆装置环境下,由于磁探针的测量将面临极大限制,因此可见光相机有可能会取代当前聚变装置中通用的磁测量手段而成为等离子体放电过程中实现位型反馈控制的方案.然而,如何利用可见光高速相机拍摄图像对托卡马克等离子体边界实现快速准确的定量评估,至今仍不清楚.
在东方超环(EAST)装置中,通过实验中记录的影像发现,在等离子体的边界区域,通常存在一条清晰可见的细窄绿色发光带,且发光带中心在三维扰动磁场[2]存在时会发生空间位置的摆动.因此,我们猜测绿光光强的空间分布一定程度上反映了边界等离子体在三维扰动场存在时的行为.如果能给出边界等离子体状态与该绿光光强空间分布的理论关系,基于一些假设,就可以建立通过测量绿光光强空间分布来重构边界等离子体状态的全新技术手段,这对于研究三维扰动磁场存在时边界等离子体的行为具有重要意义.要实现这一目标,确定绿光的具体来源并建立在给定边界等离子体状态时绿光光强空间分布的模型是最主要的理论需要之一.
由于EAST装置边界的实验过程中会采用大量锂化[3,4]作为器壁表面处理的主要手段,因此,装置边界大量存在着锂杂质.上述绿色光带的产生源于处于激发态的锂杂质的自发辐射跃迁过程中产生的波长为548 nm的Li1+特征谱线.通过理论模型分析产生该光带的物理过程,明确光带特征对于边界等离子体具体分布参数的依赖关系,进而可以为发展利用光带观测图像有效预测EAST边界等离子体行为演化这一崭新的技术手段提供理论基础.这对于深入研究三维扰动磁场对边界等离子体行为的具体影响,乃至于为发展能够有效应用于未来ITER和下一步聚变堆装置的等离子体反馈控制新的方法和思路提供重要的理论和技术储备.
本文的研究目的是建立可用于实际计算的模型,在已知边界等离子体状态时,给出所关心的Li特征谱线的光强空间分布.在接下来的第2部分中,将对Li所经历的物理过程做初步分析与描述,基于实验事实给出合理的假设以简化问题,引入作为算法基础的碰撞-辐射(collisional-radiative,C-R)模型,并基于已有的氦的C-R模型的计算结果更严谨地确认绿光对应的自发跃迁过程;在第3部分将针对所研究的具体问题,对考虑的过程以及所需速率数据的获取做明确阐述,并且给出实际用于求解的方程及边界条件的具体形式;第4部分给出基于真实等离子体状态数据的计算结果,并着重加以分析,检查基于C-R模型和相应的边界条件来描述该物理过程的合理性、可行性;第5部分是对整个工作的总结.
2 基本模型
2.1 初步分析
Li杂质经历的过程可以分为输运和碰撞-辐射跃迁两个主要的过程.输运过程包括扩散和对流,使某一能级的Li粒子在空间中产生数密度流;碰撞-辐射跃迁过程则主要包括Li粒子与磁约束等离子体的非弹性碰撞跃迁过程、Li粒子激发态的自发跃迁过程,将造成空间中某点多个能级的Li粒子互相转化.这两个过程共同影响各能级Li粒子在空间中的分布.
在聚变等离子体边界,电子数密度具有1012cm−3数量级,电子温度在10—100 eV,电子与Li发生非弹性碰撞过程的速率系数具有10−8cm3/s数量级;对于稳态放电的等离子体,其变化的时间尺度是其存在的时间尺度,通常是秒量级,而对于边界等离子体的输运过程,其时间尺度在10—100 ms的量级.所研究的等离子体状态变化的时间尺度(>10−2s)充分大于Li在空间中形成稳定分布所需要的时间尺度(10−4s),因此,结合实际获得的视频影像中发光带位置相对稳定的事实,在模型中假定:在任意时刻,Li的分布是当前等离子状态对应的稳定分布.在这一假定下,我们只需要考虑等离子体状态不随时间改变的情况.
在后面的研究中,边界磁约束等离子体的状态将被视为是研究对象Li所处的环境,忽略Li杂质对其造成的影响,其空间分布不含时且已知.并且,由于所考虑的Li元素处在磁约束等离子体的边界,等离子体温度较高,我们认为Li元素以单原子或者离子的形式存在,而不考虑其他分子形态.
2.2 C-R模型
为了定量描述上述过程,我们采用C-R模型.C-R模型早在20世纪60年代就被提出,并且被广泛应用于等离子体中各能级粒子数密度分布的计算.关于氢、氦、铝、氩、钨等元素在等离子体环境中的辐射行为,已有基于C-R模型的研究先例[5−9],在国内外的托卡马克装置中也有使用C-R模型发展诊断方法的成功实践[10,11].有关C-R模型的严格理论基础,较为全面而严谨的叙述可以参考文献[12—14],在这里仅指出与本研究相关的主要内容.
若以i表示Li电离的程度(即i=1,2,3,4分别代表Li,Li1+,Li2+,Li3+),以(i,p)表示电离状态i对应的从低到高的第p个能级,则有严格的粒子数密度方程组,
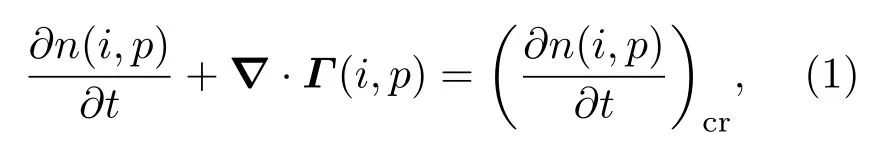
其中n表示粒子数密度,Γ表示粒子流密度,右边含脚标cr的项表示碰撞(collision)及辐射(radiation)引起的数密度变化.任意时刻,方程对所有(i,p)在空间任一点成立.
Γ(i,p)可以进一步写成
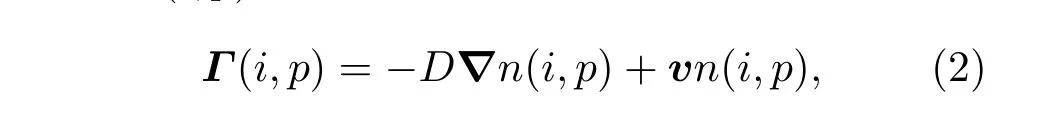
其中D是扩散系数,v是对流速度.
1)针对nα,在电离程度较高的等离子体中,电子的速率是离子的102倍数量级,碰撞截面则是10倍数量级[12,15],因此在C-R模型中,我们假定只考虑电子的碰撞作用,即nα=ne;
2)针对速率系数A以及C,现有的基于理论与实验手段所获得的数据库中,通常认为A是常数而C是电子温度T的单变量函数[15].
下面说明在这一过程中基态和亚稳态具有特殊的地位.为方便,规定符号
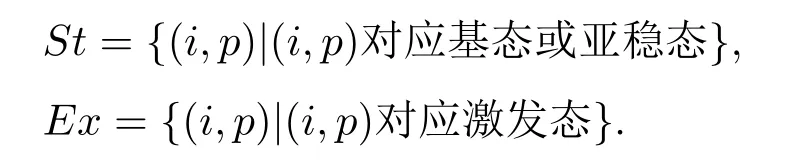
注意到,对于(i,p)∈Ex,方程(1)右边将含有向St自发跃迁对应的负项和从St能级碰撞激发对应的正项.在系统接近平衡时,由于前者正比于较大的自发跃迁系数,后者正比于较大的St粒子数密度,以至于均远大于方程(1)左边的∇·Γ(i,p)项以及项.所以,对这些激发态,我们可以只考虑C-R过程的平衡,即近似地令方程(1)左边为0,即所谓的准稳态解(quasi-steady-state-solution,QSSS)法[11].
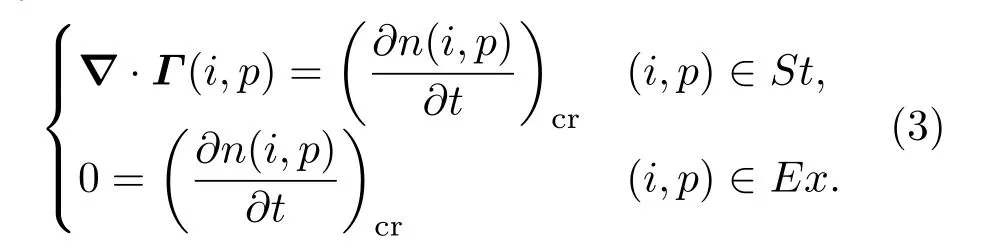
最后,在i一定时,由于对于较大的p,能级之间的间隔已经十分小,且由于它们和基态或亚稳态的能级差较大、粒子布居较少,通常将主量子数大于某一值的能级合并为p=N(i)的1个能级来考虑,或者直接忽略主量子数大于某一值能级,即我们只考虑取值在1—N(i)的p.
综上所述,基于C-R模型:
1)在这一过程中,我们仅对(i,p)∈St同时考虑输运和碰撞-跃迁过程;
2)我们只考虑有限个(i,p),对于每个(i,p),均可列出一个数密度方程,它们构成方程组(3);
3)对于(i,p)∈Ex,方程组(3)构成以St能级数密度为线性非齐次项的线性方程组,其解具有如下形式,
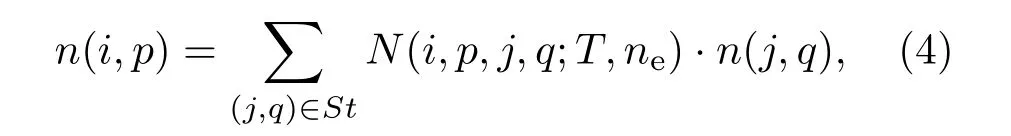
其中,系数N是电子状态T,ne的函数;
4)对于(i,p)∈St,将方程(4)代入方程组(3),将得到二阶线性方程组.
在ne与T的空间分布已知时,数值求解上述方程组(3),我们即可获得n(i,p)在空间的分布.
2.3 基于C-R模型对绿光来源的理论推理
考虑到研究的目的,最终只关心与绿光相对应的(i,p)能级在空间中的分布.如前所述,初步认定该绿光属于Li线状光谱.查阅NIST-ASD数据库或者文献[16]可以发现:Li2+在所关心范围(500—570 nm)内没有特征谱线;中性Li在范围内仅存在一条波长为527 nm的由多电子跃迁产生的谱线(1s2p3d4D→ 1s2s3d4D);Li1+则存在一条由低激发态向亚稳态跃迁的谱线(1s2p3P→ 1s2s3S),波长为548 nm,且具有较大的自发跃迁系数A(107s−1量级).
更进一步,Li1+是类He离子,其光谱结构和He类似.而关于He的C-R模型研究已Fujimoto在文献[17]中给出,文献[17]的图1给出了在T=5.7×104K,ne=6.3×1010cm−3时,He的各能级之间的转化速率图示,从中可以看出,He的三重态中存在一个明显的粒子数转化流,正是对应于1s2p3P→1s2s3S,其中包含有碰撞跃迁和自发跃迁.这说明在1s2p3P能级上,由于能级较低,且向除亚稳态外的其他能级有跃迁禁戒,He可以有较大的布居.
由于Li1+是类He离子,我们可以推测Li1+也应具有类似的结果.发光的强度正比于单位时间发射的光子数,亦即自发辐射的速率A(i,q→p)·n(i,q),可以推测Li1+1s2p3P→ 1s2s3S的自发辐射将具有较大的光强.考虑到摄相机对于光的捕捉有一定光强下限要求,判定EAST中观察到的绿光应是来自这一较强的自发辐射.按照我们之前的记号,这一跃迁表示为(2,4)→(2,2).
在之后的研究中,除了以分析具体物理过程为目的之外,我们只需要关心n(2,4)在空间中的分布即可.显然,绿光的光强正比于n(2,4)的大小,而其位置就应与n(2,4)空间分布的峰重合.
3 实例计算的准备
3.1 速率系数
要实际求解方程组(3),必须获得其中的速率系数A的大小,以及C关于T的具体函数关系.速率系数A在文献[16]中可以获得;而关于速率系数C,其主要包含有电子碰撞跃迁、电子碰撞电离、电子碰撞复合过程,已有一些相关的经验、半经验公式[18,19],然而这些公式对T的范围要求往往过于严苛,并且公式中的一些拟合系数也不易批量获得.
考虑以上原因,研究中采用了OPEN-ADAS数据库的数据.这些数据对于C-R模型而言足够全面且便于批量获得、处理,并且对T有足够广的适用范围[20].
在这里我们特别指出,实际的操作过程中,直接获得的C的数据并不是以关于T的连续函数的形式给出的,而是关于T的离散的数据点.直接从OPEN-ADAS获得的数据值分为四类:
1)自发辐射跃迁速率系数A(i,p→q);
2)电子碰撞跃迁对应的有效碰撞强度Υ(i,p → q;T)(Maxwellian averaged collision strength or the e ff ective collision strength);
3)电子碰撞电离速率系数S(i,p→i+1,q;T)和约化速率系数S′=S·exp(Eion/kT)(Eion为下能级对于的电离能,只考虑末态∈St);
4)自由电子复合速率系数R(i,p→i−1,q;T),包括单电子辐射复合和双电子复合,只考虑初态∈St.
对于1)类数据,由于是与电子状态无关的常数,我们直接使用.
对于2)类数据,相应的速率系数设为c(i,p→q;T),满足关系
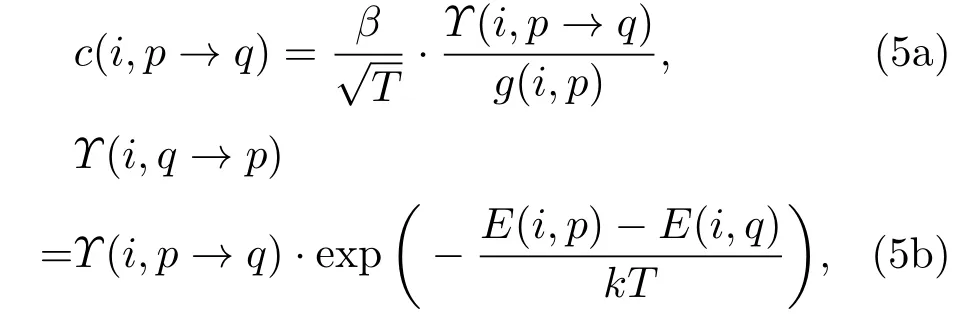
其中,在c以cm3/s为单位,T以K为单位时,数值上是(i,p)能级的统计权重(简并度);E(i,p)是(i,p)能级对应的能量.
处理时,在观察了数据点的分布后,最终选择使用二次样条曲线插值的方法,获得Υ(i,p→q;T)的插值拟合函数.其中,对于i=1的数据点,从数据库中获得的T有最大值2.00×106K(172 eV);观察对比i=3的数据点,推测Υ(1,p→ q;T)的曲线应在T>2.00×106K时趋近平缓,故在T=5.00×106K与T=2.00×107K处,按倒数2个数据点之间斜率的3/10,1/10,分别加入直线外推后的2点,之后以二次样条曲线对所有点进行插值拟合.最终由获得的Υ(i,p→q;T)插值函数代入(5a)式,即获得c(i,p→q;T).
对于3)类数据,使用二次样条曲线插值的方法,获得S′的插值拟合函数并乘上exp(−Eion/kT)即获得相应的S.
对于4)类数据,依旧使用二次样条曲线插值.其中,对于i=1的数据点,采用与2)类似的处理方式进行外推.
最终经过如上处理,从OPEN-ADAS数据库中提取出44个能级之间的速率系数数据,包含Li的9个能级,Li1+的19个能级,Li2+的15个能级,Li3+的1个能级.适用的电子温度范围为T∈(1.56 eV,1000 eV),约等于(1.80×104K,1.16×107K).
插值、外推等处理过程通过软件Mathematica 10.4.1完成.
3.2 方程与边界条件
按照上一节使用的记号,我们可以将方程(3)重新写成
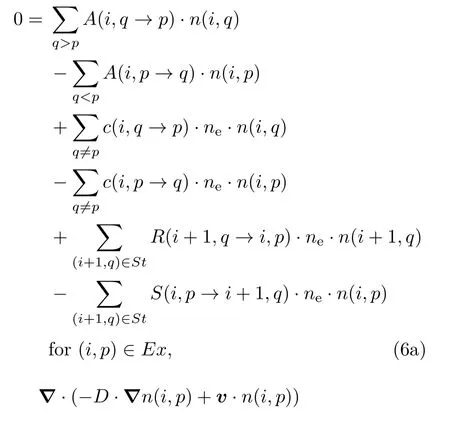
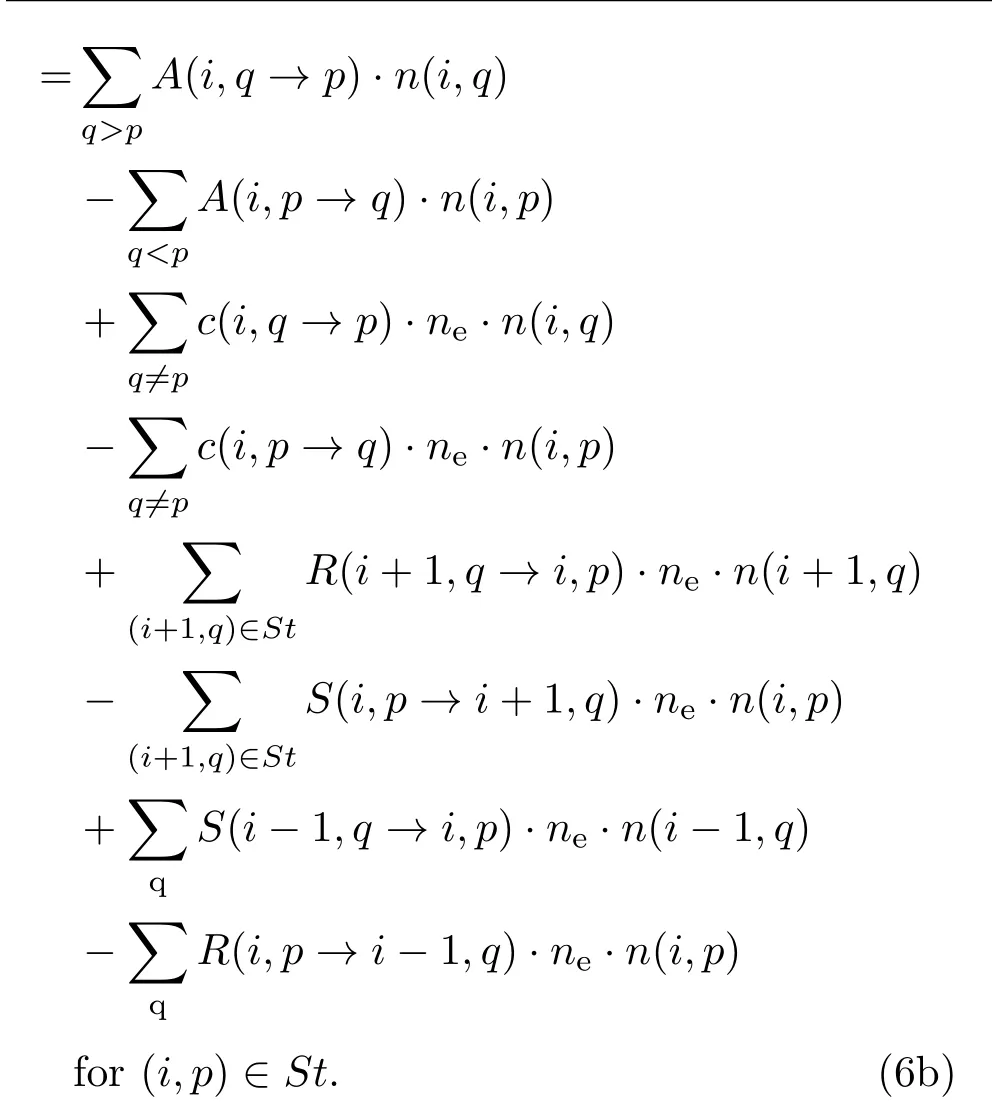
方程组(6)中,方程的个数与未知数个数是一致的(44个). 由于(6b)式是二阶微分方程组,而St={(1,1),(2,1),(2,2),(3,1),(4,1)},一般来说还需要与之相应的10个边界条件方程.为了具体地得到它们,需要基于一定的假设对输运的过程做进一步的分析.
1)我们仅考虑沿小半径径向的输运过程,近似认为装置垂直于环向的截面为圆形,即考虑一维的输运问题.从而(6b)式的左边可简化为
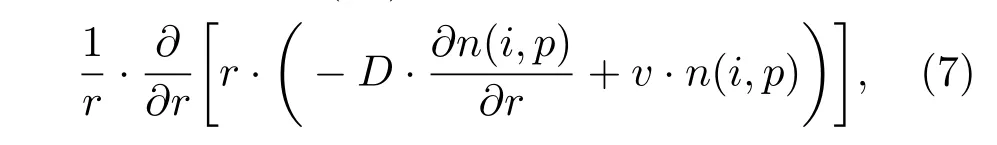
其中r即小半径位置,v是径向对流速度,规定向r增大的方向为正.
2)我们认为Li粒子的来源是由于等离子体中逃逸的粒子和装置发生碰撞,Li从中获得动能而逃逸导致的,从而可以认为Li边界上的Li具有指向内部的一个整体的漂移速度,亦即边界的对流速度v.
3)为简便起见,假定在所关心的空间范围r∈(r1,r2),D与v近似为对所有能级在空间中均恒定的常数.
4)认为D=0,即忽略扩散的作用,将Li杂质视为由边界注入的粒子流,此时方程组(6)只包含一阶的微分方程,只需要5个边界条件方程.采用这一做法主要是为了对简化数值求解方法以得到初步结果,如果要加入扩散项,则会使微分方程的数值求解变得困难.
5)认为Li粒子的源只在装置边界r=r2存在,而Li粒子的损失集中在r 6 r1部分,并且在边界r=r2处,电子温度与密度均相对较小,Li的存在形式以基态中性原子为主,从而可以假定边界条件为
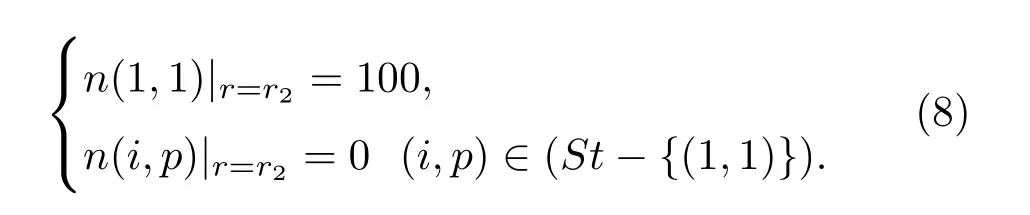
4 数值计算结果分析
基于上述模型,输入EAST边界电子温度与密度数据,用软件Mathematica 10.4.1编写对应的计算程序,使用其内置的NDSolve函数对方程进行求解.采用EAST中炮号为#63699,时间为t=4.019 s(低约束模,简称为L模)与炮号为#62585,时间为t=3.800 s(高约束模,简称为H模)的电子温度/密度分布数据(如图1).
需要指出的是,这些分布数据基于EAST多项分布诊断(包括汤姆孙散射、极化偏振干涉仪、微波反射计、弯晶谱仪等)测量,并结合磁测量结果经动理学平衡反演获得.由于目前动理学平衡反演过程并不能就仪器测量误差进一步给出误差传递结果,为测试本文提出的算法对于等离子体状态分布的测量误差的敏感性,在反演后的等离子体状态平衡分布上加上假定的±10%的不确定度(见图1中的阴影区域).将一组带有假定不确定度的分布传入程序,可输出相应的一组Li的分布曲线,这组曲线的所覆盖的区域可认为是Li的分布的置信区间,已在计算结果图2、图3中使用阴影绘出.
其中,径向位置以归一化环向磁通开根号ρ表示.而最后闭合磁面外(ρ>1)的分布数据采用最后闭合磁面以内分布拟合外推的方式获得,如图1所示.图中标注了数密度曲线的峰位置.
在多个假设的对流速度v下计算,相关计算结果如图2所示.
据此结果可知:
1)能级标记为(2,4)的Li在空间中集中分布于最后闭合磁面外(ρ>1),且其分布函数具有良好的单峰形状,这与绿光带仅在装置边缘被观察到的事实相符合;同时,也说明绿光的分布主要由最后闭合磁面外的电子状态决定,采用拟合外推的手段来获得(ρ>1)的数据可能带来较大的不准确性;
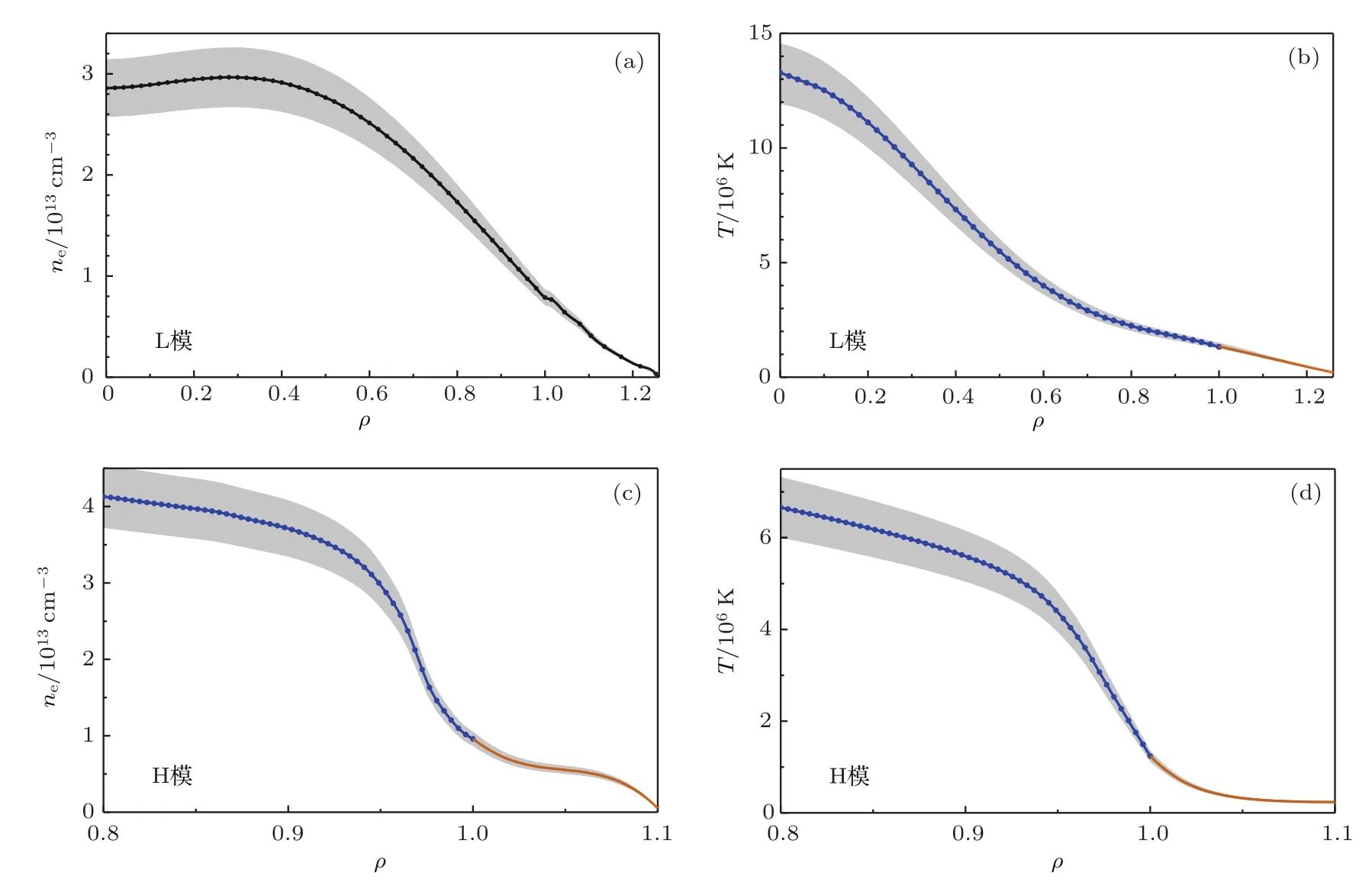
图1 (网刊彩色)EAST实际放电过程中电子温度和密度测量及拟合数据 (a)#63699炮在t=4.019 s的电子密度分布数据;(b)#63699炮在t=4.019 s的电子温度分布数据;(c)#62585炮在t=3.800 s的电子密度分布数据;(d)#62585炮在t=3.800 s的电子温度分布数据Fig.1.(color online)Electron temperature and density data in EAST:(a)Electron density data of#63699 at t=4.019 s;(b)electron temperature data of#63699 at t=4.019 s;(c)electron density data of#62585 at t=3.800 s;(d)electron temperature data of#62585 at t=3.800 s.
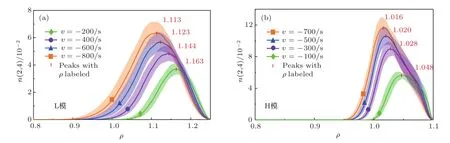
图2 (网刊彩色)数值计算结果(阴影表示置信区) (a)#63699炮在t=4.019 s的(2,4)能级的粒子数空间分布;(b)#62585炮在t=3.800 s的(2,4)能级的粒子数空间分布Fig.2.(color online)Numericalcalculation results(shaded areas stand for con fi dence regions):(a)Density of Li in state(2,4)(#63699 t=4.019 s);(b)density of Li in state(2,4)(#62585 t=3.800 s).
2)随着|v|减小,n(2,4)的峰向装置边界移动,且峰宽与峰高均减小,以L模的结果为例,当|v|由800 s−1减小至200 s−1,一方面,峰位置移动了0.05,考虑到EAST的小半径约为45 cm,这一移动大约对应1.8 cm;另一方面,峰高由0.0634减小至0.0369,半高全宽则由0.145减小至0.101,峰面积减小约至原来的2/5;可见,|v|的取值将对峰位置(绿光中心)造成一定的影响,并且会对峰面积(近似正比于总绿光强度)造成较大影响;
3)在峰的两侧,粒子数梯度较大,因此忽略扩散作用的假设将造成一定误差;可以预测,在考虑扩散的作用后,扩散将使粒子数分布具有更小的梯度,峰的宽度将会比上面计算结果大,而峰高则可能降低;
4)在边界输入相同量的Li杂质的前提下,L模下绿光的最大光强(即峰高)比H模下的要更弱,但L模下绿光在实空间的分布更宽;
5)相比L模,H模下峰位置随对流速度的变化更加不明显.
注意到置信区域以分布曲线为中心,其边界具有峰的形状.在假定10%的等离子体状态测量误差下,在算例覆盖的输运速度范围内,无论是在H模还是L模下,峰位置的偏离(置信区域边界两峰的峰位置之差)不超过0.02(约8 mm),峰高的不确定度总小于13%,半高全宽的不确定度总小于18%.可见,该算法给出的光强分布具有与等离子体状态测量误差大小相当的不确定度.
为进一步解释上面的结果,并更完整地揭示物理过程,计算了前述两种电子状态数据下其余能级在空间中的分布,如图3所示.

图3 (网刊彩色)基态与亚稳态能级的数密度空间分布,阴影表示置信区(对#63699 t=4.019 s(L模),取v=−600 s−1≈−216 m/s,结果如图中左列所示;对#62585 t=3.800 s(H模),取v=−500 s−1≈−205 m/s,结果如图中右列所示) (a)#63699 t=4.019 s亚稳态锂(2,2)的数密度;(b)#63699 t=4.019 s基态锂的数密度;(c)#62585 t=3.800 s亚稳态锂(2,2)的数密度;(d)#62585 t=3.800 s基态锂的数密度Fig.3.(color online)Densities of ground states and metastable state(2,2)with shaded areas standing for con fi dence regions(for#63699 t=4.019 s(L-mode),set v= −600 s−1≈ −216 m/s and show the results on the left.For#62585 t=3.800 s(H-mode),set v= −500 s−1≈ −205 m/s and show the results on the right):(a)Density of metastable state(2,2)(#63699 t=4.019 s);(b)densities of ground states(#63699 t=4.019 s);(c)density of metastable state(2,2)(#62585 t=4.019 s);(d)densities of ground states(#62585 t=4.019 s).
由图3结果可知:
1)如图3(b)和图3(d)所示,随径向位置ρ的减小,Li的电离程度增大,各基态的峰在该环境下互相交错、逐个出现;相比之下,H模下Li的电离程度随空间变化更快,ρ=0.90时裸原子占总粒子数Li几乎完全电离成裸原子,这是由于H模下电子温度与密度在最后闭合磁面内迅速上升导致的;
2)Li1+几乎完全分布于ρ>1,这是由于无论在L模或者H模,电子温度在ρ=1处已经大于100 eV,且具有接近1013cm−3的数密度,而Li1+的电离能仅有75.6 eV,这也解释了前文(2,4)能级集中在闭合磁面外的结果;
3)对Li1+(i=2)计算其余激发态能级的粒子数空间分布后发现,各激发态曲线形状相似、峰位置相近,数量级上有n基态≈ 100n亚稳态>1000n激发态,即基态粒子数约为亚稳态粒子数的102倍,且比激发态粒子数大103倍,并且,能级相对更高的激发态能级,(2,4)粒子数具有数量级上的优势,这与2.3节中的分析相符合,并且表明n(2,4)受更高激发态的粒子数的影响几乎可以忽略,换言之,n(2,4)几乎完全由St能级的分布决定.
5 结 论
本文基于C-R模型,提出了计算EAST中锂杂质特征谱线的光强度空间分布的实际可行方法,并收集、处理了OPEN-ADAS数据库的数据,成功编写了对应的计算程序,并在输入EAST中实测真实电子状态数据后,给出了与实验现象相符合的数值计算结果.该计算结果清晰地展现了Li杂质在向装置内输运的过程中所经历的电离、激发过程,并给出了具有良好的单峰形状的绿光空间分布,可以明确地给出其中心位置.并且,在存在±10%的等离子体状态测量误差的假定下,本文给出了计算结果的置信区间,分析表明该算法得到的光强分布的不确定度和等离子体状态测量误差相当.
通过分析计算结果,对该计算模型中针对输运系数的假设的合理性做了定性的评估,并指出了特征谱线光强分布随输运系数的变化情况,通过比较指出了绿光在L模与H模下的差异与共同特征.
值得一提的是,计算结果显示,与该绿光相对应的上能级,其上布居的粒子数相对更高的激发态能级具有数量级上的优势,表明该能级的粒子数分布主要由基态与亚稳态能级的粒子数分布决定.因此,用于实际计算模型有可能通过忽略部分高激发态能级来进一步简化.
在今后的工作中,将就更多的实例进行相应的计算,得出更具有普遍意义的结果,对这一模型做进一步修正.这一工作的成功开展,将推动建立通过测量锂杂质特征谱线光强空间分布来重构边界等离子体状态的全新技术.
感谢中国科学院等离子体物理研究所徐国盛研究员以及明廷凤博士的指导.
[1]ITER Physics Expert Groups on Con fi nement and Transport,ITER Physics Expert Group on Con fi nement Modelling and Database,ITER Physics Basis Editors 1999 Nucl.Fusion 39 2175
[2]Sun Y,Liang Y F,Qian J P,Shen B,Wan B 2015 Plasma Phys.Control.Fusion 57 045003
[3]Zuo G Z,Hu J S,Li J G,Luo N C,Hu L Q,Fu J,Chen K Y,Ti A,Zhang L L 2010 Plasma Sci.Technol.12 646
[4]Xu J C,Wang F D,Lü B,Shen Y C,Li Y Y,Fu J,Shi Y J 2012 Acta Phys.Sin.61 145203(in Chinese)[徐经翠,王福地,吕波,沈永才,李颖颖,符佳,石跃江2012物理学报61 145203]
[5]Wünderlich D,Dietrich S,Fantz U 2009 J.Quant.Spectrosc.Radiat.Transfer 110 62
[6]Goto M 2003 J.Quant.Spectrosc.Radiat.Transfer 76 331
[7]Yu Y Q,Xin Y,Ning Z Y 2011 Chin.Phys.B 20 015207
[8]Peng F,Jiang G,Zhu Z H 2006 Chin.Phys.Lett.23 3245
[9]Wang J,Zhang H,Cheng X L 2013 Chin.Phys.B 22 085201
[10]Xie H Q,Tan Y,Liu Y Q,Wang W H,Gao Z 2014 Acta Phys.Sin.63 125203(in Chinese)[谢会乔,谭熠,刘阳青,王文浩,高喆2014物理学报63 125203]
[11]Goto M,Fujimoto T 1997 Fusion Eng.Des.34 759
[12]van der Sijde B,van der Mullen J J A M,Schram D C 1984 Beitr.Plasmaphys.24 447
[13]Summers H P,Dickson W J,O’Mullane M G,Badnell N R,Whiteford A D,Brooks D H,Lang J,LochS D,GriffinD C 2006 Plasma Phys.Control.Fusion 48 263
[14]Greenland P T 2001 Proc.R.Soc.Lond.A 457 1821
[15]Janev R K 1995 AtomicandMolecularProcesses in Fusion Edge Plasmas(New York:Springer Science+Business Media)pp9–63
[16]Wiese W L,Fuhr J R 2009 J.Phys.Chem.Ref.38 565
[17]Fujimoto T 1979 J.Quant.Spectrosc.Radiat.Transfer 21 439
[18]Kato T,Nakazaki S 1989 At.Data Nucl.Data Tables 42 313
[19]Voronov G S 1997 At.Data Nucl.Data Tables 65 1
[20]Summers H P,O’Mullane M G 2011 AIP Conf.Proc.1344 179
PACS:52.25.Vy,52.55.Fa,52.70.KzDOI:10.7498/aps.66.125201
A collisional-radiative model for lithium impurity in plasma boundary region of Experimental Advanced Superconducting Tokamak∗
Zhang Tai-Yang1)Chen Ran2)†
1)(School of Nuclear Science and Technology,University of Science and Technology of China,Hefei 230022,China)
2)(Institute of Plasma Physics,Heifei Institute of Physical Science,Chinese Academy of Sciences,Hefei 230031,China)
4 January 2017;revised manuscript
2 April 2017)
A green emission layer caused by lithium impurity is universally observed in plasma boundary region of Experimental Advanced Superconducting Tokamak(EAST)via a visible-light camera,where lithium coating is normally adopted as a routine technique of wall conditioning.In this article,in order to estimate the spatial distribution of green light intensity of this emission layer according to the given real parameter distributions of edge plasmas,a practicable method is proposed based on a collisional-radiative model.In this model,a fi nite number of energy levels of lithium are taken into account,and proper simpli fi cations of convection-di ff usion equations are made according to the order-of-magnitude analysis.We process the atomic data collected from the OPEN-ADAS database,and develop a corresponding program in Mathematica 10.4.1 to solve the simpli fi ed one-dimensional problem numerically.Estimation results are obtained respectively for the two sets of edge plasma pro fi les of EAST in L-mode and H-mode regimes,and both clearly show a good unimodal structure of the spatial distribution of green light intensity of this emission layer.These analyses actually provide the spatial distributions of lithium impurities at di ff erent energy levels,not only indicating the spatial distribution of the intensity of this emission layer induced by lithium impurity but also revealing the physical processes that lithium experiences in edge plasma.There are some di ff erent and common characteristics in the spatial distribution of the intensity of this emission layer in these two important cases.This emission layer is kept outside the last closed magnetic surface in both cases while it becomes thinner with a higher intensity peak in H-mode case.Besides,the sensitivity of this algorithm to the measurement error of edge plasma pro fi le is also explored in this work.It is found that the relative errors of the numerical results obtained by our proposed method are comparable to those of edge plasma pro fi les.This work provides important theoretical references for developing a new practical technique of fast reconstructing edge plasma con fi gurations in EAST based on the emission of lithium impurity,and may further contribute a lot to the studies of edge plasma behaviors when three-dimensional perturbation fi elds are adopted.
impurities in plasma,tokamak,collisional-radiative model
10.7498/aps.66.125201
∗国家自然科学基金(批准号:11675220)资助的课题.
†通信作者.E-mail:chenran@ipp.ac.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant No.11675220).
†Corresponding author.E-mail:chenran@ipp.ac.cn
