随机电磁高阶Bessel-Gaussian光束在海洋湍流中的传输特性∗

刘永欣 陈子阳 蒲继雄

(华侨大学信息科学与工程学院,福建省光传输与变换重点实验室,厦门 361021)

随机电磁高阶Bessel-Gaussian光束在海洋湍流中的传输特性∗

刘永欣 陈子阳 蒲继雄†

(华侨大学信息科学与工程学院,福建省光传输与变换重点实验室,厦门 361021)

(2017年1月14日收到;2017年3月14日收到修改稿)

利用广义惠更斯-菲涅耳衍射积分公式得到了随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输的交叉谱密度矩阵的一般表达式,通过数值计算主要研究了随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输时其在远场输出面的统计特性的变化,包括归一化光谱强度、光谱偏振度、两点的光谱相干度等.数值模拟结果显示海洋湍流能够对随机电磁高阶Bessel-Gaussian光束的归一化光谱强度分布产生影响,随着传输距离的增加,零阶Bessel-Gaussian光束中心出现凹陷,高阶Bessel-Gaussian光束中心会变平坦继而又凹陷下去,不管零阶还是高阶,当传输距离增加到足够远,光强分布都会演变成最终的类高斯分布.x轴上各点的偏振度改变与相干长度δxx,δyy以及海洋湍流参数有关.x轴上任意一点和原点这两点的光谱相干度也随x的增加而呈振荡变化,并且海洋的均方温度耗散率χT对光谱相干度有影响.

海洋湍流,随机电磁光束,高阶Bessel-Gaussian光束,传输

1 引 言

最近,随着海洋探测和光通信技术的发展,光在海洋中的传输、成像引起了人们的兴趣,人们逐渐认识到研究激光束受到海洋湍流影响的必要性.2011年,Korotkova研究小组[1−3]采用一种由温度和盐度共同组成的综合模型的能谱先后研究了海洋湍流对高斯-谢尔模型电磁光束的偏振度和光谱的影响,以及高斯光束在海洋湍流传输中光强以及相干特性的变化.随后,激光束在海洋湍流中的传输也激发了国内各研究者的研究热情[4−16].Fu等[4,5]研究了部分相干径向偏振空心光束和多高斯-谢尔模型光束经过海洋湍流的传输特性;浙江大学赵道木等先后研究了电磁涡旋光束和电磁非均匀相干光束经过海洋湍流的传输[7−9],以及随机各向异性电磁光束在海洋湍流中的光谱变化[10];四川师范大学季小玲等[11,12]研究了海洋湍流对高斯阵列光束以及部分相干环状偏心光束的传输特性的影响;四川大学Huang等[13]研究了海洋湍流和阵列光束参数对光束质量的影响;Liu等[14−16]研究了海洋湍流对啁啾高斯脉冲光束光谱特性的影响以及平顶涡旋空心光束经海洋湍流传播的光强特性等.可见,激光束在海洋湍流中的传输研究是一个研究热点.

而高阶Bessel-Gaussian光束除了具有无衍射和自重建特性以外,还因为螺旋相位因子的存在而具有轨道角动量,是一类典型的涡旋光束.人们对高阶Bessel-Gaussian光束在自由空间中的自重建特性以及在ABCD光学系统和大气湍流中的传输特性都进行了深入研究[17−21],但在海洋湍流中的研究未见有报道.另外,利用轨道角动量可以对信息进行编码与传输,从而应用于光通信等领域,可见该光束还在光通信领域具有巨大的潜在应用价值.基于以上几点有必要对高阶Bessel-Gaussian光束在海洋湍流中的传输特性进行研究.本文主要研究随机电磁高阶Bessel-Gaussian光束在海洋湍流中的传输特性,讨论其归一化光谱强度、光谱偏振度、光谱相干度的变化规律.

2 理论推导

考虑随机电磁高阶Bessel-Gaussian光束在海洋湍流中沿着Z轴传输,在Z=0平面(即源平面)该光束的二阶相干和偏振特性可以由一个2×2的交叉谱密度矩阵来描述

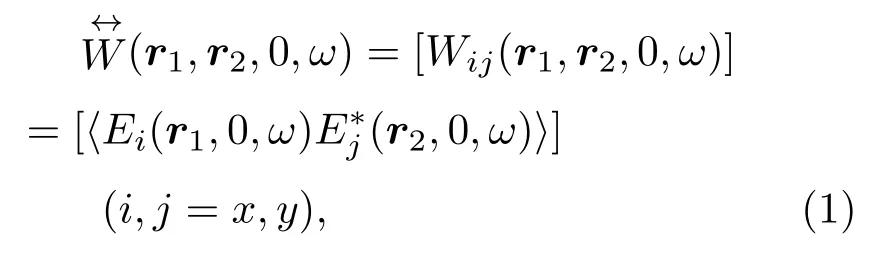
式中,r1,r2是Z=0平面上两点的位矢,ω是角频率,星号表示复共轭,尖括号表示系综平均.为简便起见,假设在源平面的光束的交叉谱密度矩阵的非对角元素为零,即Wxy(r1,r2,0,ω)=Wyx(r1,r2,0,ω)=0,则源平面的交叉谱密度矩阵可简化为

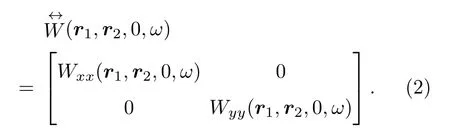
对于高阶Bessel-Gaussian光束其矩阵元可表示为

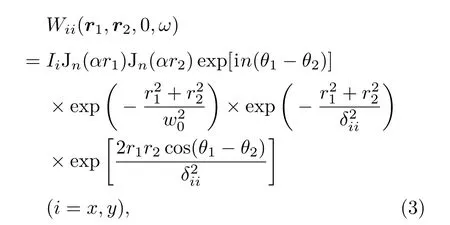
式中,Ii=E2i0;r1,r2是位矢r1,r2的模;Jn表示贝塞尔函数;n表示拓扑荷数;w0是束腰宽度;δii是ii方向的相干长度.

当此光束在海洋中传输时,根据广义的惠更斯-菲涅耳原理,利用源平面的交叉谱密度矩阵元可得到在海洋湍流中传输到Z=z平面的交叉谱密度矩阵元为

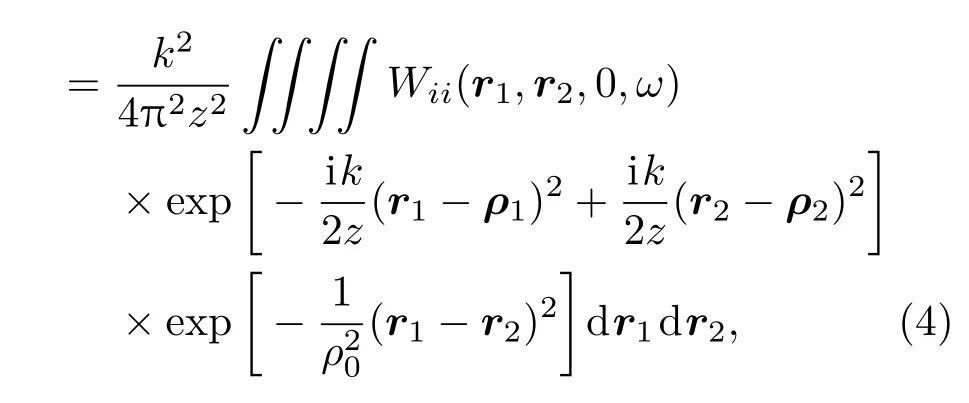
式中,k=2π/λ是波数,其中λ是波长;ρ1,ρ2是Z=z平面上两点的位矢;ρ0是球面波在海洋湍流介质中传播后的相干长度,表示为

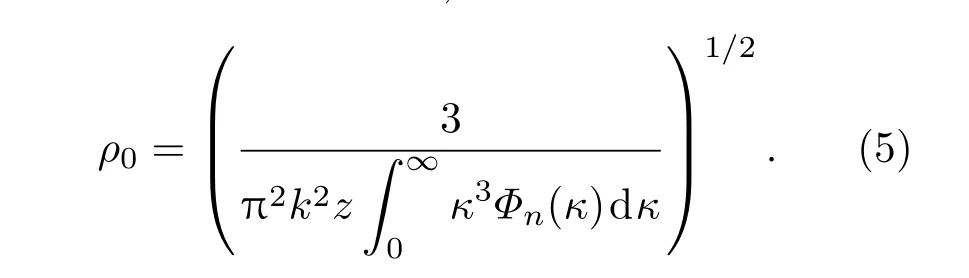
关于海水折射率波动的空间能谱模型可以从文献[1,22]中得到,这个模型是由温度波动和盐度波动组成的二元线性多项式.当海洋湍流是各向同性和均匀的时,这个模型是成立的,那么经过特殊化考虑之后的一维谱可写成

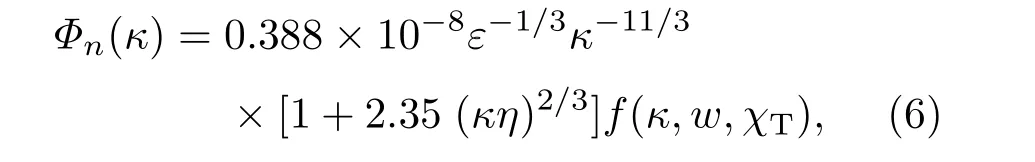
式中,ε是单位质量液体中的湍流动能的耗散率,取值可以从10−4m2/s3到10−10m2/s3;η =10−3m是Kolmogorov微尺度(内尺度);f(κ,w,χT)可以表示为

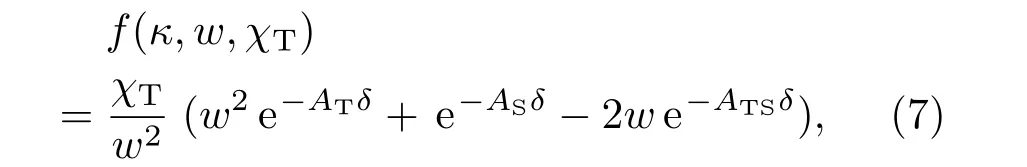
其中,χT是均方温度耗散率,AT=1.863×10−2,AS=1.9× 10−4,ATS=9.41× 10−3,δ=8.284(κη)4/3+12.978(κη)2,w是温度和盐度波动的相对强度,海洋当中的取值是−5到0,取−5时说明由盐度引起的湍流占主导,取0时说明由温度引起的湍流占主导[1].

将(3)式代入(4)式后经过繁琐的积分计算,最后化简可得到随机电磁高阶Bessel-Gaussian光束在海洋中传输一段距离后的交叉谱密度矩阵元为

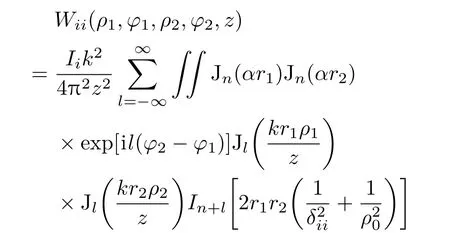
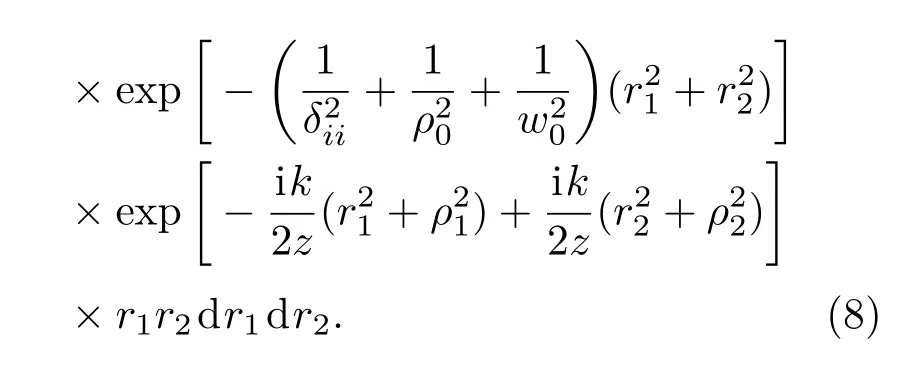
令(8)式中ρ1= ρ2= ρ,φ1= φ2= φ可得到在z平面任意点(ρ,z)的光谱强度和光谱偏振度分别为

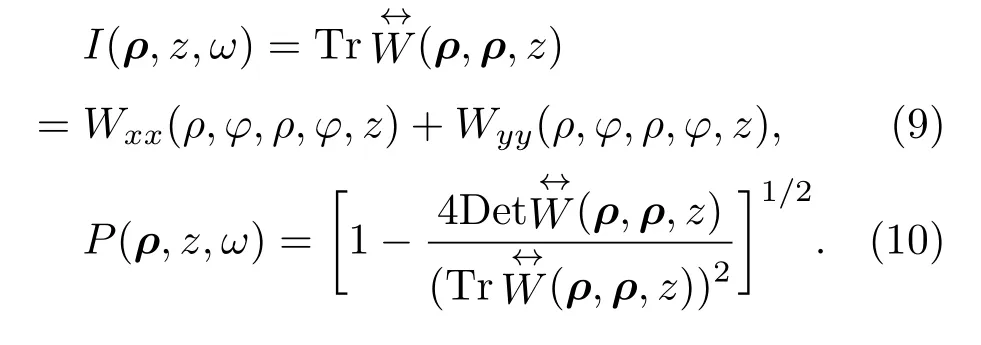
式中,Det,Tr分别表示的是矩阵的行列式和迹的值.

因为Wxy(ρ1,ρ2,z,ω)=Wyx(ρ1,ρ2,z,ω)=0,则(10)式化简为

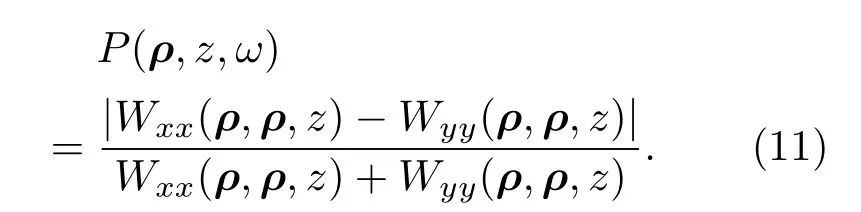
另外,在z平面上任意两点的光谱相干度根据其定义式可表示为

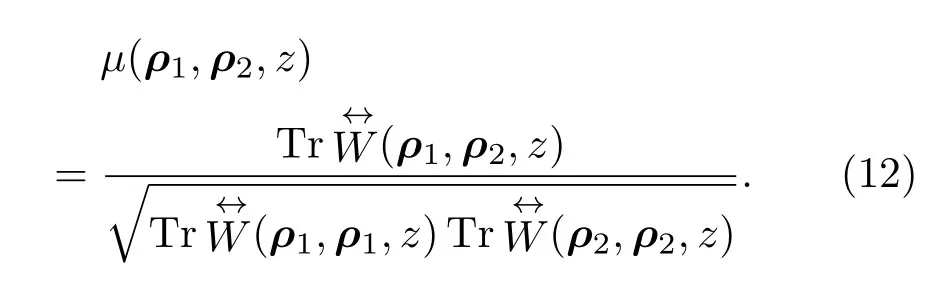
令ρ1=x,φ1=0,ρ2=0,φ2=0,即x轴上任意一点和原点这两点的光谱相干度,则(12)式表示为

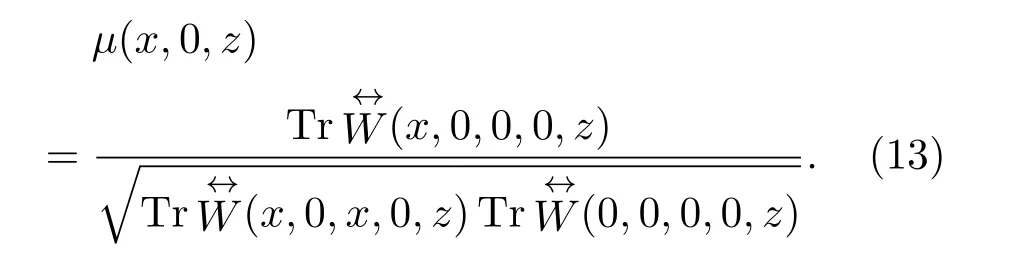
3 数值计算与模拟

利用数学软件Mathematica对(8)—(13)式进行编程,计算并模拟得到归一化光谱强度(I(ρ,z,ω)/I(ρ,z,ω)max) 以及光谱偏振度、光谱相干度的变化规律,如图1—5所示.另外,若无特殊说明,计算参数一般为λ=632.8 nm,α =500,w0=0.02 m, δxx= δyy=0.01 m,Ix=Iy=1,η =10−3m,ε=10−7m2/s3,w= −2.5,χT=10−10K2/s.

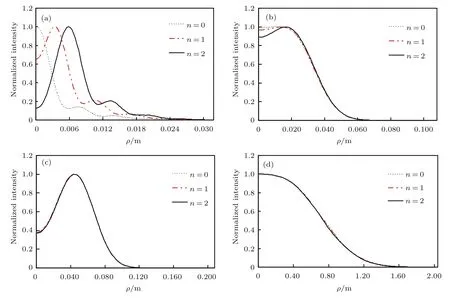
图1 (网刊彩色)不同拓扑荷数的随机电磁Bessel-Gaussian光束在海洋中传输到不同距离处的归一化光强分布(a)z=100 m;(b)z=500 m;(c)z=1 km;(d)z=10 kmFig.1.(color online)Normalized intensity of stochastic electromagnetic Bessel-Gaussian beams with di ff erent topological charge at several propagation distances passing in the oceanic turbulence:(a)z=100 m;(b)z=500 m;(c)z=1 km;(d)z=10 km.

图1是不同拓扑荷数的随机电磁Bessel-Gaussian光束在海洋中传输到不同距离处的归一化光强分布.由图1(a)可知,对于拓扑荷数n=0的零阶Bessel-Gaussian光束其归一化光强分布具有高斯型分布,而对于n̸=0的高阶Bessel-Gaussian光束,其光斑的中心是一个暗核,且拓扑荷数n越大,中间的凹陷越深,暗核也越大.但随着传输距离的增加,由于海洋湍流的影响,零阶Bessel-Gaussian光束中心也出现凹陷,高阶Bessel-Gaussian光束中心会变平坦继而又凹陷下去,整体而言光斑会逐渐展开变大,到一定传输距离,各阶Bessel-Gaussian光束的归一化光强近似分布一致,再经过足够长的传输距离,中心凹陷性光强曲线最终都会演化为类高斯曲线,如图1(d)所示.

图2是拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流中传输z=100 m处归一化光强分布.由图2(a)可知,随着海洋的均方温度耗散率χT的增加,一阶Bessel-Gaussian光束中心的凹陷越小,而当χT6 10−10时,χT对光强分布的影响已不再明显.图2(b)是在不同ε(单位质量液体中的湍流动能的耗散率)的海洋湍流中的归一化光强分布,随着ε的变大,Bessel-Gaussian光束中心的凹陷越深,但ε>10−7时,ε对光强分布的影响变化已很小.图2(c)是在不同w(温度和盐度波动的相对强度)的海洋湍流中的归一化光强分布,随着w的变大,Bessel-Gaussian光束中心的凹陷越小,但w 6−2.5时,w对光强分布的影响变化也很小.总之,随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输时,海洋湍流参数的强弱对光强分布会产生影响,但影响都是有界限的.

图3是拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输z=1 km处x轴上各点的偏振度的变化,其中δxx=0.02 m,Ix=1,Iy=0.5,其他参数不变.由图3可知,当δxx= δyy=0.02 m时,偏振度随着x的增加将保持不变且与源平面的值(0.33)相等,这是因为当δxx= δyy时,对于任意一点,(8)式的交叉谱密度矩阵元除了Ii这个系数不同,其他参数都相同, 可得Wyy(ρ,ρ,z)=0.5Wxx(ρ,ρ,z), 再代入(11)式计算可得P(ρ,z,ω)=1/3. 而当δxx̸= δyy时,偏振度随着x的增加而发生变化,但变化规律与δyy的大小有密切关系,当δxx< δyy时,随着x的增加偏振度先减小再增大;而当δxx>δyy时,随着x的增加偏振度变化规律更复杂,如图3(b)所示.

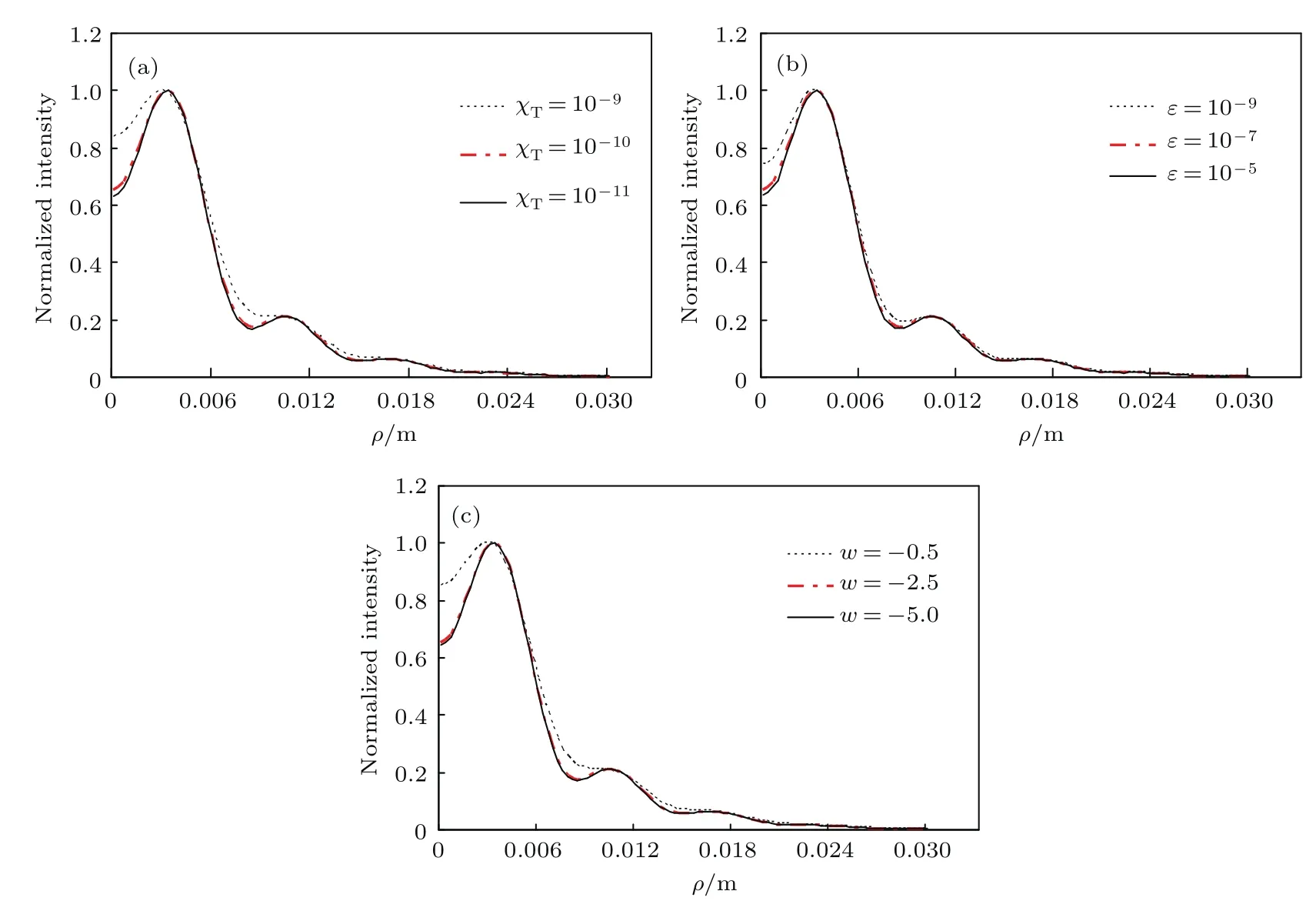
图2 (网刊彩色)拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流中传输z=100 m处归一化光强分布Fig.2.(color online)Normalized intensity of stochastic electromagnetic high-order Bessel-Gaussian beams with n=1 at z=100 m passing in the oceanic turbulence with di ff erent parameters.

图4是拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流中传输z=1 km处x轴上各点的偏振度的变化,其中δxx=0.02 m,δyy=0.03 m,Ix=1,Iy=0.5,其他参数不变. 由图4可知,随着海洋的均方温度耗散率χT的增加或者w(温度和盐度波动的相对强度)的增加,x轴上各点的偏振度改变幅度减小直至均趋于0.33(源平面的值)附近.

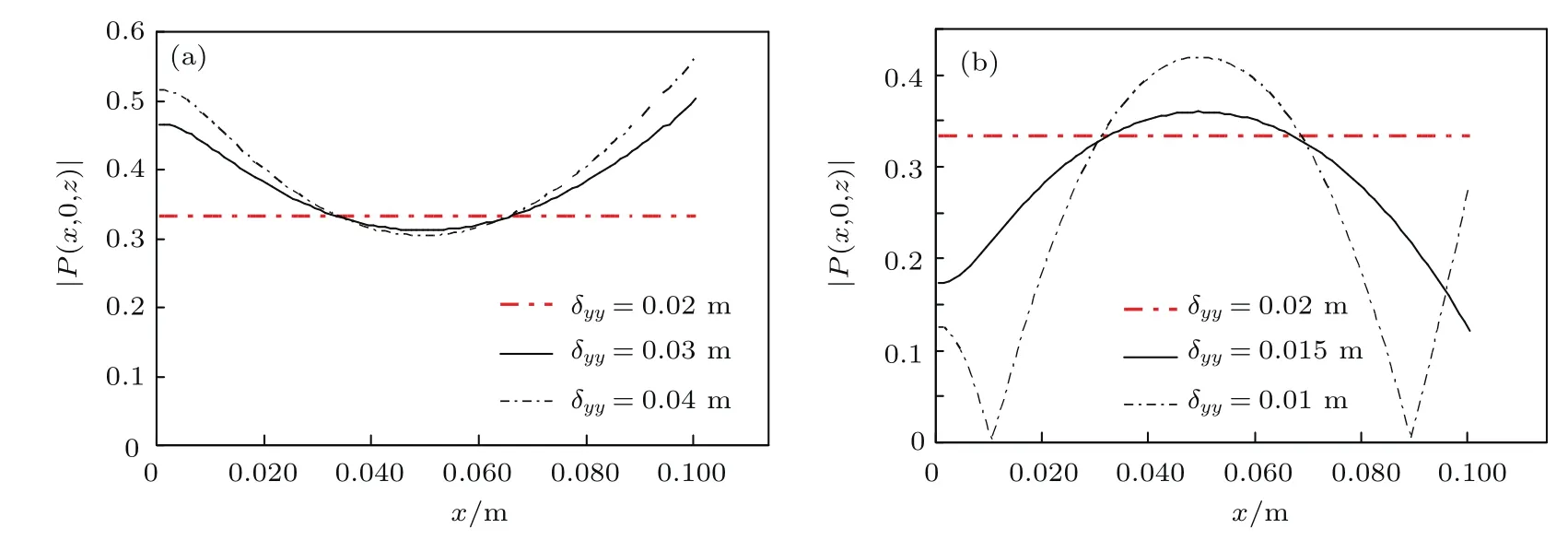
图3 (网刊彩色)拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输z=1 km处x轴上各点的偏振度的变化(其中δxx=0.02 m,Ix=1,Iy=0.5,其他参数不变)Fig.3.(color online)Changes of the polarization of stochastic electromagnetic high-order Bessel-Gaussian beams with n=1 at z=1 km passing in the oceanic turbulence.The other parameters are the same except that δxx=0.02 m,Ix=1,Iy=0.5.

图4 (网刊彩色)拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流中传输z=1 km处x轴上各点的偏振度的变化(其中δxx=0.02 m,δyy=0.03 m,Ix=1,Iy=0.5,其他参数不变)Fig.4.(color online)Changes of the polarization of stochastic electromagnetic high-order Bessel-Gaussian beams with n=1 at z=1 km passing in the oceanic turbulence with di ff erent parameters.The other parameters are the same except that δxx=0.02 m, δyy=0.03m,Ix=1,Iy=0.5.

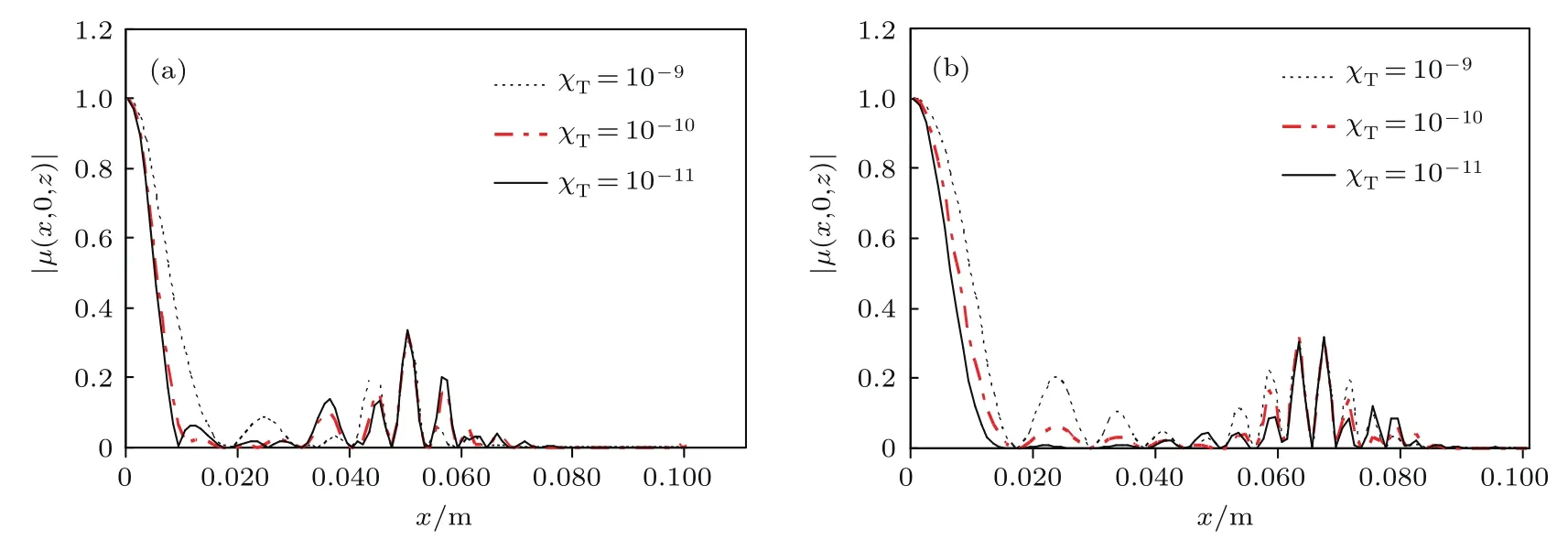
图5 (网刊彩色)拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流传输到z处x轴上任意一点和原点这两点的光谱相干度的变化 (a)z=500 m;(b)z=1 kmFig.5.(color online)Changes of the spectral degree of coherence of stochastic electromagnetic high-order Bessel-Gaussian beams with n=1 at z plane passing in oceanic turbulence with di ff erent parameters:(a)z=500 m;(b)z=1 km.

图5是拓扑荷数n=1的随机电磁高阶Bessel-Gaussian光束在不同海洋湍流传输到z处x轴上任意一点和原点这两点的光谱相干度的变化.由图可见,随着x远离原点,两点的光谱相干度呈振荡变化,并且随着海洋的均方温度耗散率χT的增加,振荡变化的幅度稍加剧烈.比较图5(a)与图5(b)可知,当海洋的均方温度耗散率χT不变时,随着传输距离的增加,光束光斑展开变大,光谱相干度也随着逐渐展开.

4 结 论

利用广义惠更斯-菲涅耳衍射积分公式得到了随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输的交叉谱密度矩阵的一般表达式,并在此基础上主要研究了随机电磁高阶Bessel-Gaussian光束在海洋湍流中传输时其在远场输出面的统计特性的变化,包括归一化光谱强度、光谱偏振度、两点的光谱相干度等.数值模拟结果显示海洋湍流能够对随机电磁高阶Bessel-Gaussian光束的归一化光谱强度分布产生影响.在海洋传输中,零阶Bessel-Gaussian光束中心也出现凹陷,高阶Bessel-Gaussian光束中心会变平坦继而又凹陷下去,整体而言光斑会逐渐展开变大,到一定传输距离,各阶Bessel-Gaussian光束的归一化光强近似分布一致,再经过足够长的传输距离,不管零阶还是高阶,光强分布都会演变成最终的类高斯分布.x轴上各点的偏振度改变与δxx,δyy有关.当δxx=δyy=0.02 m时,偏振度随着x的增加将保持不变且与源平面的值相等;当δxx̸=δyy时,偏振度随着径向距离的变化而改变.x轴上任意一点和原点这两点的光谱相干度也随x的增加而呈振荡变化,并且海洋的均方温度耗散率χT对光谱相干度有影响.该研究内容对高阶Bessel-Gaussian光束在海洋中的光通信、光成像以及海底探测等领域的应用具有潜在价值.

[1]Korotkova O,Farwell N 2011 Opt.Commun.284 1740

[2]Shchepakina E,Farwell N,Korotkova O 2011 Appl.Phys.B 105 415

[3]Farwell N,Korotkova O 2012 Opt.Commun.285 872

[4]Fu W Y,Zhang H M 2013 Opt.Commun.304 11

[5]Fu W Y,Zhang H M,Zheng X R 2015 Chin.J.Lasers 42 s113002(in Chinese)[付文羽,张汉谋,郑兴荣2015中国激光42 s113002]

[6]Tang M M,Zhao D M 2013 Appl.Phys.B 111 665

[7]Xu J,Tang M M,Zhao D M 2014 Opt.Commun.331 1

[8]Xu J,Zhao D M 2014 Opt.Laser Technol.57 189

[9]Tang M M,Zhao D M 2014 Opt.Commun.312 89

[10]Zhu W T,Tang M M,Zhao D M 2016 Optik 127 3775

[11]Lu L,Ji X L,Li X Q,Deng J P,Chen H,Yang T 2014 Optik 125 7154

[12]Yang T,Ji X L,Li X Q 2015 Acta Phys.Sin.64 024206(in Chinese)[杨婷,季小玲,李晓庆 2015物理学报 64 024206]

[13]Huang Y P,Huang P,Wang F,Zhao G,Zeng A 2015 Opt.Commun.336 146

[14]Liu D J,Wang Y C,Wang G Q,Yin H M,Wang J R 2016 Opt.Laser Technol.82 76

[15]Liu D J,Chen L,Wang Y C,Wang G Q,Yin H M 2016 Optik 127 6961

[16]Liu D J,Wang Y R,Yin H M 2015 Appl.Opt.54 10510

[17]Zhang Q A,Wu F T,Zheng W T,Pu J X 2011 Sci.Sin.:Phys.Mech.Astron.41 1131(in Chinese)[张前安,吴逢铁,郑维涛,蒲继雄 2011中国科学:物理学 力学 天文学41 1131]

[18]Chen B S,Chen Z Y,Pu J X 2008 Opt.Laser Technol.40 820

[19]Chen Z Y,Cui S W,Zhang L,Sun C Z,Xiong M S,Pu J X 2014 Opt.Express 22 18278

[20]Zhao C L,Wang L G,Lu X H,Chen H 2007 Opt.Laser Technol.39 1199

[21]Eyyuboglu H T 2007 Appl.Phys.B 88 259

[22]Nikishov V V,Nikishov V I 2000 Int.J.Fluid Mech.Res.27 82

PACS:42.68.Xy,42.25.–p,42.25.Kb,42.30.LrDOI:10.7498/aps.66.124205

Propagation of stochastic electromagnetic high-order Bessel-Gaussian beams in the oceanic turbulence∗

Liu Yong-Xin Chen Zi-Yang Pu Ji-Xiong†

(Fujian Key Laboratory of Light Propagation and Transformation,College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China)

14 January 2017;revised manuscript

14 March 2017)

Recently,the laser beam propagation in the oceanic turbulence has become a hot research topic.In addition to the characteristics of free di ff raction and self-reconstruction,the high-order Bessel-Gaussian beam is a kind of typical vortex beam because of the existence of a spiral phase factor with orbital angular momentum.Researchers have investigated the self-reconstruction property of the high-order Bessel-Gaussian beams in the free space,also carried out intensive researches on the transmission characteristics of high-order Bessel-Gaussian beam in the ABCD optical system and in the atmospheric turbulence.However,to the best of our knowledge,to date there has been no investigation on the propagation of this laser beam in the oceanic turbulence.In this paper,we will study the propagation characteristics of the random electromagnetic high-order Bessel-Gaussian beams in the oceanic turbulence,and discuss the variation of the normalized spectrum intensity,the spectral degree of polarization,and the spectral degree of coherence.By using the extended Huygens-Fresnel di ff raction integral formula,the general expression for the cross spectral density matrix of the stochastic electromagnetic high-order Bessel-Gaussian beams propagating in the oceanic turbulence is obtained,and the statistical properties of the random electromagnetic high-order Bessel-Gaussian beams propagating in the seawater are investigated by numerical calculation.The numerical results show that the oceanic turbulence can a ff ect the normalized spectral intensity distribution of the random electromagnetic beam.With the increase of the transmission distance,the center of the zero-order Bessel-Gaussian beam becomes depressed,and the center of the higher-order Bessel-Gaussian beam will become fl at and then depressed.As the transmission distance increases far enough,regardless of the zeroorder or higher-order,the intensity distribution will eventually evolve into the quasi Gaussian shaped distribution.The variation of the degree of polarization of each point on the x axis is related to the coherence length(δxx,δyy)and the oceanic turbulence parameters.The spectral coherence of the origin and any point on the x axis also changes with the increase of x,and the rate of dissipation of mean-square temperature χThas in fl uence on the spectral coherence.This research is of great value for applying the high-order Bessel-Gaussian beam to the optical communication,optical imaging and underwater exploration in the ocean.

oceanic turbulence,stochastic electromagnetic beam,high order Bessel-Gaussian beam,propagation

10.7498/aps.66.124205

∗国家自然科学基金(批准号:61505059,61575070,11504116)、福建省教育厅科技项目(批准号:JA15038)和华侨大学高层次人才启动经费(批准号:12BS231)资助的课题.

†通信作者.E-mail:jixiong@hqu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.61505059,61575070,11504116),the Project of Education Department of Fujian Province,China(Grant No.JA15038),and the High level talent research of Huaqiao University,China(Grant No.12BS231).

†Corresponding author.E-mail:jixiong@hqu.edu.cn