环序数和序数差对牛顿环测量透镜曲率半径的影响研究

李仁文

(合肥师范学院 电子信息工程学院，安徽 合肥 230601)



环序数和序数差对牛顿环测量透镜曲率半径的影响研究

李仁文

(合肥师范学院 电子信息工程学院，安徽 合肥 230601)

针对学生在牛顿环实验中提出的问题，本文通过对实验数据处理进行分析，指出牛顿环实验数据采集和数据处理过程中选取环序数和序数差应注意事项，并指出在数据处理过程中使用绘图拟合软件Origin进行线性拟合得到曲率半径的方法是可行的。

牛顿环实验；数据采集；数据处理

1 问题提出

利用牛顿环干涉测量透镜曲率半径是理工科学生大学物理实验中非常重要的实验项目，学生在实验中不但熟悉了读数显微镜的使用方法更加深了对等厚干涉现象的理解[1]。笔者从事大学物理实验教学十余年，发现学生在实验操作和数据处理过程中经常遇到以下两点疑惑：

(1)实验过程中需要采集的数据较多，靠近中央暗斑环序数较低的干涉条纹虽然清晰但是由于形变导致测量质量不好，究竟应该从第几条开始测量；

(2)传统的实验数据处理方法有直接计算法、逐差法、最小二乘法、作图法等。采用直接计算法时环序数差(m-n)究竟选取多大较为合适没有定论，导致学生在处理数据求得透镜曲率半径的过程中经常出现一些错误。而在坐标纸上通过作图法来计算曲率半径，由于手工作图偏差较大导致最终结果误差更大。

鉴于此，本文对实验测量数据进行处理与分析，指出实验数据采集和处理过程中选取环序数和序数差应遵循的规律，解决以上疑惑。

2 牛顿环干涉测透镜曲率半径实验原理简介[1,2]

牛顿环干涉属于分振幅方法获得相干光形成的干涉，如图1所示，一块曲率半径很大的平凸透镜的凸面和另一块平玻璃板相接触时在两玻璃板间形成一空气薄膜，当一束波长为的单色光垂直入射通过空气薄膜的上下表面依次反射而产生两束相干光进行叠加干涉，由于光程差仅取决于光入射位置处的薄膜厚度，是一种等厚干涉。从反射光方向观察，将看到一组以接触点为中心的明暗相间的同心圆形干涉条纹，由于两玻璃镜接触之间难免有灰尘附着并且受力形变，实际观察到中心点是一个暗斑。假设平凸透镜的曲率半径为R，第k级干涉条纹的半径为rk，由直角三角形勾股定理和半波损失额外程差不难得到干涉暗环满足：

(1)

由于中央暗斑中隐藏的干涉级数修正值j未知，要想测量透镜曲率半径R，通常选取环序数分别为m和n的两条条纹，它们分别满足：

(2)

(3)

上面两式相减，可以得到：

(4)

因此可以通过精确测量任意两条环序数为m和n的干涉环半径(或直径dm和dn)，就可以准确测量出透镜的曲率半径R：

(4)

或者

(5)

图1 牛顿环干涉装置示意图

3 数据采集

表1 牛顿环实验原始数据

4 数据处理

4.1 直接计算法

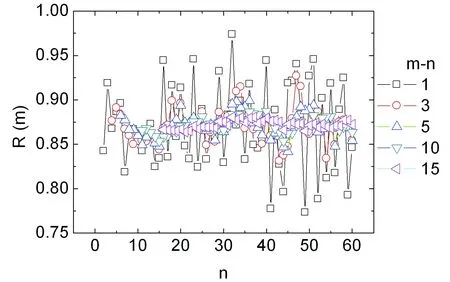
图2 环序数差(m-n)分别为1，3，5，10和15按照公式(5)计算所得曲率半径R随环序数的关系

如表1所示，对表中各干涉环左右位置相减得到各环的直径，代入公式(5)，按照环序数差(m-n)分别为1，3，5，10和15计算得到曲率半径R。这可以利用微软excel或者Origin软件快速计算得到。如图2所示为不同环序数差下计算得到的曲率半径R随环序数n的变化关系。由图可见，环序数差对曲率半径计算结果影响较大。环序数差小于5时(如1和3)，计算结果波动极大，最大超过10%；而环序数差大于5时波动较小；当环序数差等于10和15时波动较小趋于稳定。另外还可以看出干涉环序数对曲率半径测量结果也有影响。当采用环序数小于10的干涉环时，图中数据点曲线上翘明显，说明环序数越小曲率半径计算结果偏差越大；而采用环序数大于10的干涉环计算时，数据点曲线趋于平稳，说明测量结果偏差较小。这是由于越靠近中央接触点，条纹形变越大导致干涉环直径测量误差越大。对环序数差(m-n)为10的曲率半径计算结果求平均得到R=0.871m，这和仪器厂商提供的参数以及文献报道[3]的结果是相符的。所以为减小实验误差，在实验时应从第10环以后测量数据，这和文献报道[4]的从第5环以后测量的观点是相符的，其中文献[4]所使用的透镜半径几乎是笔者实验使用透镜半径的两倍。这也可能说明，透镜半径越大，低环序数的选取对结果的影响越小。

4.2 作图拟合法

5 结语

由上述分析可以看出，在牛顿环干涉测透镜曲率半径实验中，为减小误差，应采集离开中央暗斑环序数大于10以上的干涉环直径；采用直接计算法计算曲率半径时，环序数差(m-n)要取的大些，至少应

大于5；采用作图拟合法时，可以结合Origin绘图拟合软件利用计算机较简便、快速地计算出曲率半径。

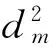
图3 干涉环直径的平方和环序数m的变化关系，方块符号为实验数据，直线为拟合曲线

[1] 杨述武.普通物理实验[M].北京：高等教育出版社，2001.

[2] 章韦芳，李大创，訾振发.大学物理实验[M].北京：人民邮电出版社，2013.

[3] 滕坚.牛顿环实验数据处理方法分析[ J] .物理通报, 2006 (6):34-36 .

[4] 刘才明，许毓敏. 对牛顿环干涉实验中若干问题的研究[J].实验室研究与探索，2003(6):13-14.

[5] 胡素梅，陈海波.基于Origin的牛顿环实验数据处理方法[J].吉首大学学报，2006(6):50-52.

Studying the Influence of Ordinal Number and Ordinal Number Difference on Lens Curvature Radius in Newton Ring Experiment

LI Renwen

(SchoolofElectronicandInformationEngineering,HefeiNormalUniversity,Hefei230601,China)

In view of the students'questions on Newton ring experiment, this paper attempts to analyze the experimental data and points out some matters which need attention in data collection and processing about the ring ordinal number and its difference. It is practical to use Origin software in data processing to obtain the radius of curvature of lens by linear fitting.

Newton ring experiment; data collection; data processing

2017-01-05

合肥师范学院2015年校级科研项目(2015TD02)

李仁文(1979-)，博士，安徽人，合肥师范学院副教授，主要从事物理教学和研究。

O4

B

1674-2273(2017)03-0055-03