等价无穷小性质及应用的教学拓展研究

解大鹏

(合肥师范学院 数学与统计学院, 安徽 合肥 230601)



等价无穷小性质及应用的教学拓展研究

解大鹏

(合肥师范学院 数学与统计学院, 安徽 合肥 230601)

利用等价无穷小的性质处理函数极限问题是微积分中处理函数极限的一类重要的方法。本文较为系统地归纳了等价无穷小的性质， 通过实际算例重点阐明这些性质在函数极限问题中的应用，并且针对不同的情形， 给出了一些方法和建议。

等价无穷小；极限；应用

等价无穷小概念属于微积分学中最基本的概念，同时也是比较重要的概念。大多数《数学分析》和《高等数学》教材都或详或略地对这方面内容有所涉及。然而，不少教材却存在内容编排不尽合理和个别知识点表述不够严谨等问题，导致很多读者很难掌握这部分内容。因此, 有必要对等价无穷小进行深入的探讨。

等价无穷小具有很好的性质，很多应用问题都会或多或少的与这些性质相关，掌握并充分利用好等价无穷小的性质, 往往会使一些复杂的函数极限问题简单化， 可起到事半功倍的效果，很多学者对此做了大量的研究，参看文献[1-6]。为了使教师们更加准确地理解和把握这部分教学内容，使“等价无穷小”在教材中发挥其应有的作用，本文将在相关学者研究的基础上全面系统地归纳等价无穷小的性质及其在函数极限问题中的应用。

1 教学困惑

在讲授等价无穷小代换求极限的内容时经常会遇到利用等价无穷小替换求有和、差运算的分式极限问题。 有些算例虽然做法不符合常理但结果正确这让学生很费解，而且现有教材普遍存在对利用等价无穷小替换求有和、差运算的分式极限问题表述不恰当或欠严谨的情况，大致可以分为以下几类情形[1]:

(1)认为若对和差运算作等价代换，则要出错。

(2)认为加减运算不能进行等价代换。

(3)认为加减运算一般不能进行等价代换。

(4)对该问题未予说明。

(5)给出了关于和差运算的代换定理。

这会导致教师对此问题讲解不到位，以至于学生在实际应用等价无穷小代换计算函数极限时产生困惑，导致解题过程错误百出, 有时甚至还很难判断错在什么地方。因此, 有必要对等价无穷小的性质进行深入的讨论，以便恰当运用, 达到简化运算的目的。

2 等价无穷小性质的推广及在求函数极限中的应用

等价无穷小的基本性质：设f,f1,g,g1,h均为同一自变量变化过程中的无穷小,则

(1)等价无穷小的反身性：f～f；

(2)等价无穷小的对称性：若f～g，则g～f；

(3)等价无穷小的传递性：若f～g,g～h，则f～h；

这些属于等阶无穷小的基本性质，将其推广到更为广泛的函数类中时，可以起到简化计算的作用。

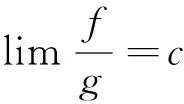
解 当x→0时，arctanx3～x3,arcsin2x3～2x3,ln(1+x3)～x3,sin32x～8x3，故有

于是，由定理1可知，

由这个定理，还可以推广到n个函数和的等价无穷小：

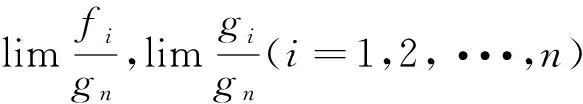
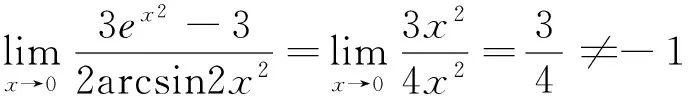
所以由定理2可得

正如以上性质定理所描述的那样，把等价无穷小代换推广到和与差的形式，能够适用的函数类范围也随之扩大，于是简化了函数的极限运算过程。在运用这些性质定理时容易忽略条件而乱用或错用得到错误计算结果， 因此解题时需要尤为注意。

错解 当x→0时，有

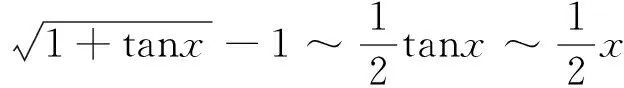
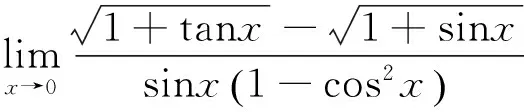
定义1[4]设f(x)在U(x0)内n阶可导且存在正整数k使得

f(x0)=f′(x0)=f″(x0)=···=f(k-1)(x0)=0,f(k)(x0)≠0

则称f(x)在x0处满足k阶条件。

解 令f(x)=cosx-e-x2,g(x)=x+ln(1-x)，则有

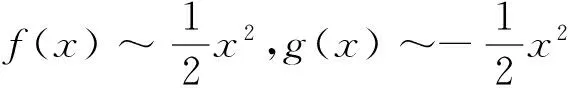
下面的定理，能更好的在幂指函数求极限中运用等价无穷小代换。

定理5[5]设在x=x0的某个去心领域内，f(x)与g(x)连续，且当x→x0时，f(x)→1,g(x)→，则。

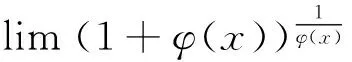
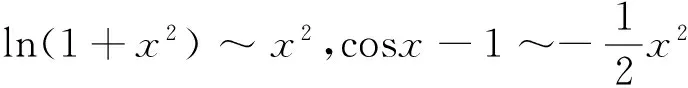
在求含变上限积分的极限中，如果恰当选用等价无穷小代换，可将问题转化为简便易求的极限形式．常用的几种变上限积分的等价无穷小公式为：当x→0时，

直接使用洛必达法则可以证明以上公式(证明略)。

例7 求极限

解 由变上限积分的等价无穷小公式可知：

由上述例题可以看出被积函数之间都是等价无穷小，所以可以得到被积函数用等价无穷小代换后的变上限积分仍然是等价无穷小，可推出如下定理：

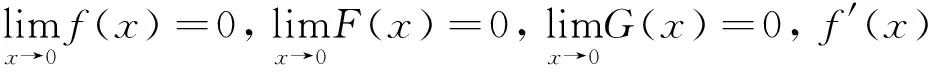
由定理7还能列出一些上面未列出的等阶无穷小公式，如：

例8 求极限

本例也可使用洛必达法则来求解， 但若使用洛必达法则来求解则会使得解题过程非常繁琐，而且易于出错，而恰当运用等价无穷小代换的方法则会收到意想不到的效果．

4 教学建议

根据以上分析，下面就该节内容的教学提出几点建议:

(1)引导学生发现并修正教材中表述不够严谨之处，并借此强调，要善于思考，

敢于质疑。

(2)引导学生积极养成发散思维的习惯。在补充、扩展和深化时，教师不要一味地告诉学生将要发生什么、该怎么做，而是要引导他们自己去寻找和发现。如在补充和一般化等价代换关系、补充和差函数等价代换定理时，可用巧妙的提问，引导学生去探索、发现、归纳、总结、证明和应用。

(3)扩充的内容要恰当而适度。补充和差函数的等价代换定理和无穷小的运算律，例题补充多少，难度控制在什么程度，等等，这些都要结合各专业课程标准等具体情况具体分析。另外，还要将对解决这些问题有帮助的参考书籍及参考论文和网址等告知学生，为学生自主探索指明道路[1]。

5 结束语

等价无穷小代换求两个无穷小之比的极限时，若所求的函数为分式，可以同时代换整个分子和整个分母，也可用等价无穷小代换整个分子或分母。但不能随意对分子或分母中的某个加项用等价无穷小替换来求得。对于不同的情形， 给出了相应的措施只有选择合适的等价无穷小替换，才能正确求得有和，差分式的极限。等价无穷小代换时，应第一时间判断函数是否符合各性质定理的条件，这一点非常重要。在求极限时，若不能满足等价无穷小代换的条件时，应该先对所求极限函数进行化简，使之符合等价无穷小代换的条件。求极限过程中，等价无穷小代换可与其它方法结合使用。

[1] 潘建辉，胡学刚，邓志颖．关于“无穷小的比较”的教学研究[J]．高等数学研究，2011，14(5)：43-46．

[2] 龚萍．等价无穷小的性质及其运用推广[J]．河北理工大学学报(自然科学版)，2009，31(3): 102-105．

[3] 魏晓娜，李曼生．等价无穷小的应用研究[J]．数学教学研究，2010，29(10)：59-61．

[4] 蹇小平．极限求解中等价无穷小量替换条件的推广[J]．湖北民族学院学报(自然科学版)，2011，29(3)：254-257．

[5] 周斌．等价无穷小的性质与运用[J]．内江科技，2011，4(4)：93．

[6] 李秀敏．王灵色．等阶无穷小在求极限过程中的应用[J]．高等数学研究， 2002，5(3)：36-37．

Research on Teaching Expansion of Equivalent Infinitesimal Nature and Application

XIE Dapeng

(SchoolofMathematicsandStatistics,HefeiNormalUniversity,Hefei230061,China)

The properties of function limit problem of equivalent infinitesimal is one of the most important methods in the calculus of function limit processing. In this paper, the properties of equivalent infinitesimal are systematically summarized, and the applications of these properties in the limit of function are emphasized with the practical examples. Some methods and suggestions are given for different conditions.

equivalent infinitesimal; limit; application

2017-01-20

安徽省高等学校自然科学研究重点项目(KJ2015A196)

解大鹏( 1981-) ，男，吉林洮南人，讲师，硕士，主要从事微分方程及大学数学教学。

O171; G642

B

1674-2273(2017)03-0039-04