一种新的超混沌系统修正函数投影同步

朱红旗,张秀兰

（淮南师范学院金融学院，安徽 淮南 232038）

数学、计算机研究

一种新的超混沌系统修正函数投影同步

朱红旗,张秀兰

（淮南师范学院金融学院，安徽 淮南 232038）

针对一种新的超混沌系统，基于Lyapunov稳定性理论建立同步控制器。该控制器在实现任意初值的超混沌系统修正函数投影同步的同时，能保证闭环系统所有信号有界。数值仿真的结果也验证了该方法的有效性。

同步；修正函数投影同步；超混沌系统

1引言

自从Ott等提出OGY方法控制混沌系统以来①Ott E,Grebogi C,Yorke J A."Controlling chaos",Physical Review Letters,1990,64(11):pp.1196-1199.，对混沌系统的控制已成为非线性科学的研究热点，并提出了许多有效的控制方法，如PID控制②Chezi L L,Peccardi C."PID control of a chaotic system:An application to an epidemiological model".Automatic,1997,33(2):pp.181-191.，自适应状态反馈控制③Feki M."An adaptive feedback controller for linearizable chaotic systems".Chaos,Solitons&Fractals.2003, 15(5):pp.883-890.，滑模控制④Ablay G."Sliding mode control of uncertain unified chaotic systems".Nonlinear Analysis:Hybrid systems, 2009,3(4):pp.531-535.，自适应模糊控制⑤Boulkroune A,Chekireb H,Tadjine M."Observer-based adaptive feedback controller of a class of chaotic systems".International Journal of Bifurcation and Chaos,2006,16(2):189-196 Liu H,Li S,Sun Y，Wang H. Prescribed performance synchronization for fractional-order chaotic systems".Chinese Physics B,2015,24(9): 090505.Poursamad A,Markazi A H D."Adaptive fuzzy sliding-mode control for multi-input multi-output chaotic systems".Chaos,Solitons&Fractals,2009,42(5):3100-3109.等。混沌系统的同步问题作为混沌控制的一个重要方面在信息处理，通讯安全，生态系统中得到广泛的应用⑥Liu H,Li S,Wang H,Huo Y,Luo J.Adaptive synchronization for a class of uncertain fractional-order neural networks.Entropy,2015,17(10):7185-7200.。目前，学者们提出了多种同步方法，如完全同步、时滞同步、修正函数同步、投影同步及修正函数投影同步等⑦Liu H,Li S,Wang H,Huo Y,Luo J."Adaptive synchronization for a class of uncertain fractional-order neural networks",Entropy,2015,17(10):7185-7200.Carroll T L,Heagy J F,Pecora L M."Transforming signals with chaotic sychronization.Phys Rev E,1996,54:4676-4680,.Rosenblum M G,Pikovsky AS,Kurths J." From phase to lag synchronization in coupled chaotic oscillatrors".Phys Rev Lett,1997,78:4196-4193. Mainieri R,Rehacek J.Projective synchronization in three-dimensional chaotic systems.Phys Rev Lett, 1999,82:pp.3042-3045.刘恒，李生刚，孙业国，王宏兴：《带有未知非对称控制增益的不确定分数阶混沌系统自适应模糊同步控制》，《物理学报》2015年第7期，第64页。。其中，投影同步因为能使两个混沌系统按照一定的比例因子进行同步，由于比例因子的不可预测性能使保密通信更加安全可靠。近来，在投影同步的基础上学者们进一步提出了修正函数投影同步⑧Du H，Zeng Q,Wang C".Function projective synchronization of different chaotic systems".Phys Rev Lett, 2008,372:pp.5402-5410.。

2009年，刘明华等提出了一种新的超混沌系统①刘明华，冯久超：《一个新的超混沌系统》，《物理学报》2009年第7期，第4457-4462页。。目前，对于这种混沌系统的研究较少。本文主要针对刘混沌系统的修正函数投影同步问题，基于Lyapunov稳定性理论，设计自适应同步控制器，并对同步的效果进行仿真研究。

2问题的描述

一种新的超混沌系统可以描述为：

其中,[x,y,z,w]T为可测量的系统状态向量，a,b,c,d为系统参数。当参数的取值为a=35,b=3,c=35,d=8时系统(1)表现出混沌现象,如图1所示。

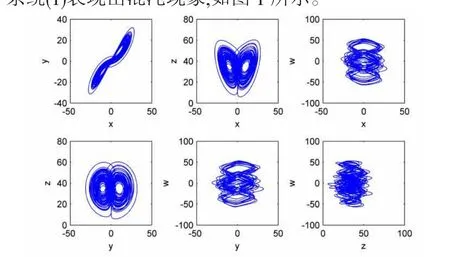
图1超混沌系统(1)的混沌吸引子

为表述方便，记x=[x,y,z,w]T，f(x)=[a(y-x),cx-xz+ w,-bz+xy,-dx]T，则超混沌系统可以改写为：

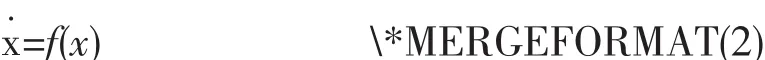
同步中，取驱动系统如(2)式，响应系统为：

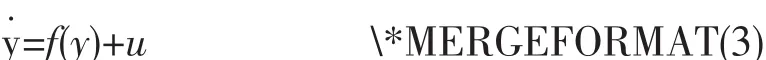
其中y∈R4为可测的系统状态向量，u∈R4为控制输入。

首先给出如下的同步误差定义：

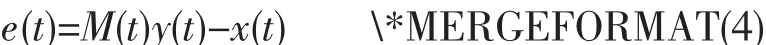
这里M(t)=diag[m1(t),···m4(t)]为函数比例因子矩阵，mi(t)≠0为连续可微的函数。本文的控制目标为选取适当的控制量u，在保证闭环系统所有信号有界的前提下实现响应系统(3)及驱动系统(2)的修正函数投影同步，即：

3同步控制器的设计及稳定性分析

根据(2)-(4)，同步误差的动态方程为

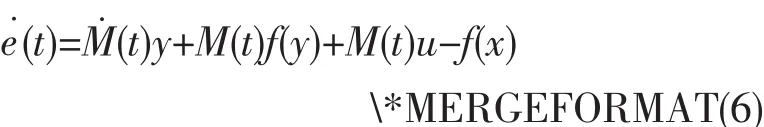
于是，根据(6)控制量u可选为

其中，K=diag[k1,k2,k3,k4,]，ki＞0,i=1,2,3,4为设计参数。于是有下面的结论成立：

定理1对于超混沌驱动系统（2）和响应系统（3），设控制量为（7），则可实现两混沌系统任意初值的修正函数投影同步，且所有闭环系统信号有界。

证明：把控制量方程（7）带入其误差动态方程，有：

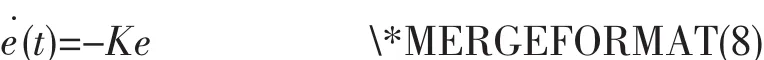
选取Lyapunov函数为：

则V对时间t的导数为

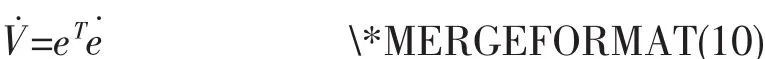
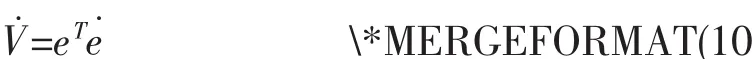
根据方程(8)可得

4

其中k=min{ki},i=1,2,3,4。根据(11)求解微分方程可得：

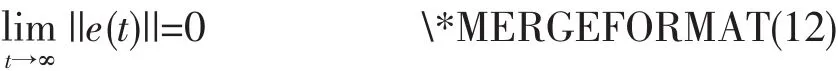
且闭环系统所有信号有界。证毕。

4数值仿真

仿真中，系统参数选择如下：k1=k2=k3=k4=1。参数k取值较小是为了说明本文设计的同步控制器良好的控制效果。

超混沌系统(2)和(3)的系统参数都选为a=35, b=3,c=35,d=8。系统的初值为：

x=[0,0,40,2]T,y=[-5,-5,-20,-10]T

修正函数比例因子矩阵选为M(t)=diag[2+sint,

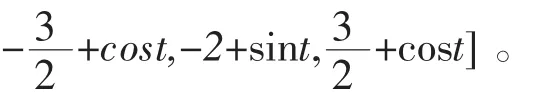
仿真的结果见图2-图5。图2为驱动系统状态变量随时间的变化，图3为响应系统在控制量（7）的作用下状态变量的变化。图4为同步误差。图5为控制输入变量。

从仿真的结果可以看出修正函数投影同步效果较好，本文设计的控制器能很好地实现任意初值的两超混沌系统的修正函数投影同步。从图2-5可以看出，整个闭环系统在保证实现同步的过程中，两系统所有信号及控制输入均有界。

图2驱动系统状态变量变化曲线

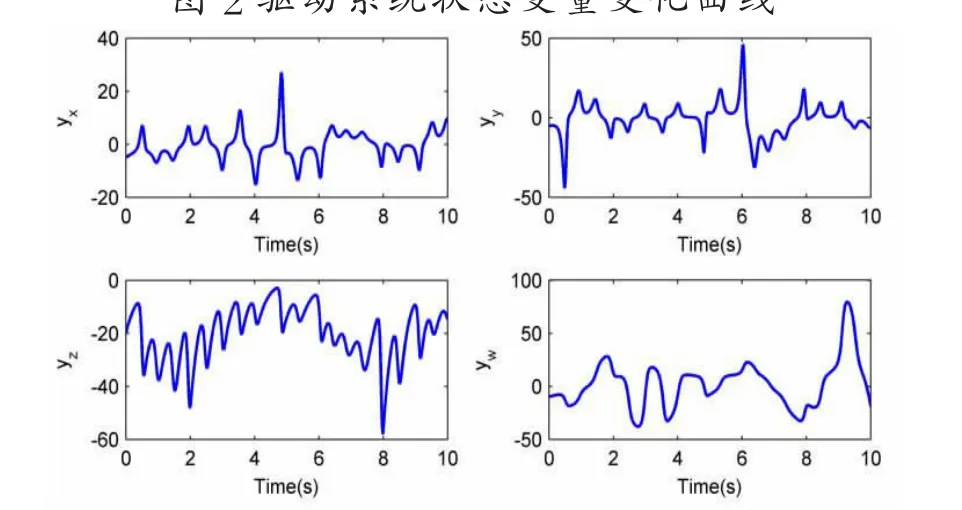
图3响应系统状态变量变化曲线

图4修正函数投影同步误差

图5控制量变化曲线

5结论

针对一种新的超混沌系统，基于Lyapunov稳定性理论研究任意初值的超混沌系统的修正函数投影同步问题。构建的同步控制器能很好地实现两系统的修正函数投影同步。最后，数值仿真的结果也进一步验证了本文控制方法的有效性。

A ne w hyper-chaotic system for projective synchronization of modified function

ZHU Hongqi,ZHANG Xiulan

A synchronization controller is established based on Lyapunov stability theory for the new hyper-chaotic system.The controller makes it possible for any initial value to be projected synchronously and guarantees that all signals in the closed-loop system will remain bounded.The effectiveness of the proposed scheme is illustrated throughout simulation results.

synchronization;projective synchronization of modified function;hyper-chaotic system

TP273

A

1009-9530（2017）03-0085-03

2017-03-09

朱红旗(1967－)，女，淮南师范学院金融学院讲师，研究领域：非线性系统控制。张秀兰(1981－)，女，淮南师范学院电子工程学院讲师，研究领域：混沌控制与同步。