海上大气波导传播抛物方程模型的算法研究
2017-08-07孟书生
孟书生
(郑州科技学院基础部,河南郑州450064)
海上大气波导传播抛物方程模型的算法研究
孟书生
(郑州科技学院基础部,河南郑州450064)
根据电波传播的角谱理论原理,考虑两种极化波在导体、阻抗和粗糙边界层面上具有不同的反射系数,在初始场和分步傅里叶变换求解的过程中加入反射系数影响,从而得到可一致计算水平或垂直极化波传播特性的新算法.通过仿真计算电波在蒸发波导、粗糙海面情况下的传播损耗,并与APM(Advanced Propagation Model)的预测结果进行比较,验证了该算法的有效性.
大气波导;抛物方程;角谱;边界条件
海面存在大气波导时,电波传播损耗预测的精度对岸基或舰载雷达性能评估结果影响很大.随着计算电磁学的发展,人们能够通过数值求解抛物方程方法实现近海面复杂对流层环境中的电波传播特性预测.抛物方程是由Leontovich和Fock于1946年首先提出[1],但是直到1973年,Hardin在海洋声学中提出抛物方程的SSFT(Split-step Fourier Transform)算法[2]后,抛物方程才在海洋声学、光传播和无线电波传播等领域得到了长足发展.20世纪80年代末至今,Sirkova I,Mikhalev M等人广泛地开展了基于抛物方程的对流层电波传播模型与算法研究[3],使抛物方程方法成为目前解决复杂大气和地(海)面条件下远距离电波传播问题最有效的手段.研究表明,平静海面上低入射余角水平极化波传播可按导体边界条件处理,但是垂直极化波传播和两种极化波在海浪较大时,传播损耗计算需考虑阻抗或海面粗糙度的影响[4].Hitney根据波导模理论在粗糙海面条件下的计算结果,得到修正抛物方程模型SSFT算法的经验公式[5].Dockery等人采用DMFT(Discrete Mixed Fourier Transform)计算阻抗或粗糙海面条件下的传播损耗[6-7].Hannah在研究自由空间GPS信号传播时,基于抛物方程模型仿真多径波导环境下,边界为任意导体、阻抗或粗糙面时可采用一致的形式和过程计算水平或垂直极化波传播特性的新算法[8].笔者对新算法进行了仿真计算,并与APM(Advanced Propagation Model)的预测结果进行了比较.
1 抛物方程模型
抛物方程是波动方程的近似形式.取电磁场时谐因子为e-iwt,以标量ψ表示电磁场的某一场分量.在空间直角坐标系(x,y,z)下,假设ψ与y无关,即其只随水平距离(x轴)和高度(z轴)变化,则水平极化波中只有Ey为非零电场分量,可设ψ=Ey,而垂直极化波中只有Hy为非零磁场分量,则可设ψ=Hy.电波传播过程中,ψ满足二维标量波动方程[9]:

式(1)中:k0为自由空间波数,n为大气折射指数.
定义沿x轴正向传播的波函数为:

把式(2)代入式(1)并进行不同的近似,就可以得到所谓的标准抛物方程和一种常用的宽角抛物方程形式,分别如式(3)和式(4)所示:
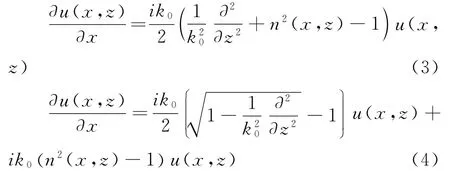
标准抛物方程是窄角抛物方程中的一种,在传播仰角小于15°时具有很好的计算精度.上述形式的宽角抛物方程在计算传播仰角小于30°时都有较好的精度,两者都可以用SSFT算法求解.
2 SSFT算法
抛物方程的数值算法主要有三种:SSFT、有限差分法和有限元法.SSFT相对于其他算法,距离向步进Δx可以取很大,并且利用基于FFT(Fast Fourier Transform),因此计算速度快.有限差分法和有限元法在处理地形边界条件时具有一定优势,采用何种算法与具体应用有关.在大气波导条件下研究近海面远距离的电波传播问题,出于计算效率方面的考虑,宜采用SSFT算法.
2.1 SSFT求解形式
标准抛物方程的SSFT求解形式如式(5),

式(5)中:p为变换域变量,F和F-1分别表示傅里叶变换和逆变换,下同.
式(4)中所表示的宽角抛物方程的SSFT求解形式如式(6),

抛物方程中傅里叶变换定义为:
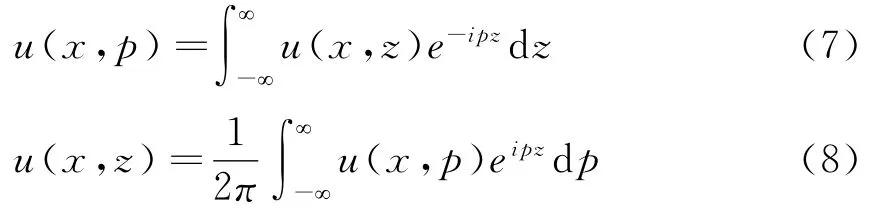
与傅里叶变换把时间域函数变换到频域类似,抛物方程中傅里叶变换是把空间函数变换到角度域,其物理意义可以用平面波角谱来解释.与惠更斯原理不同,角谱法提供了解释传播过程的另一种观点,它认为在某一平面上的波场,可以用沿各不同方向传播的平面波叠加而成,所有这些平面波组成该波长的角谱,角谱中的每一平面波各自独立地传播.空间某一点的波场就是角谱中的平面波传到该处后叠加的结果.
式(5)~(8)中p=k0sinθ,θ为平面波分量与水平面夹角,式(8)表示某一平面上的波场用沿各不同方向传播的平面波叠加而成.
2.2 初始场
抛物方程必须要在一定的初始条件和边界条件下才能求解,其初始场一般通过对发射天线方向图函数进行傅里叶逆变换得到.
初始位置处场的垂直分布与天线方向图f(p)为傅里叶变换对:

考虑地面效应,设场的镜像为A0(x0,z),则其傅里叶变换为f0(p),即:

若与x轴夹角为θ的平面波分量反射系数为R(p),则实际上变换域镜像场则为R(p)f0(p),有:

初始场则为:

如果发射天线高度为z0米,仰角为θelev,那么用f(p-p0)e-ipz0代替f(p)即可,其中:p0=k0sin(θelev).
2.3 边界条件
2.3.1 地表边界
平静海面可视为光滑阻抗表面,此时水平和垂直极化的反射系数分别为:

其中:ε=εr+i60λσ是复介电常数,εr为相对介电常数,σ为电导率.海面εr和σ值可根据CCIR建议(1986)计算获得.
海上风速较大时,需考虑海面粗糙度的影响,粗糙海面反射系数Rr为:
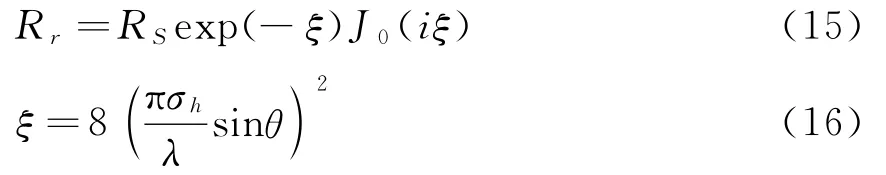
式中:RS为光滑表面的反射系数,J0为零阶贝塞耳函数;σh为海面均方根高度:

u表示风速,单位m/s.理想导体边界条件下,水平极化反射系数RH=-1,垂直极化反射系数RV=1.
2.3.2 上边界
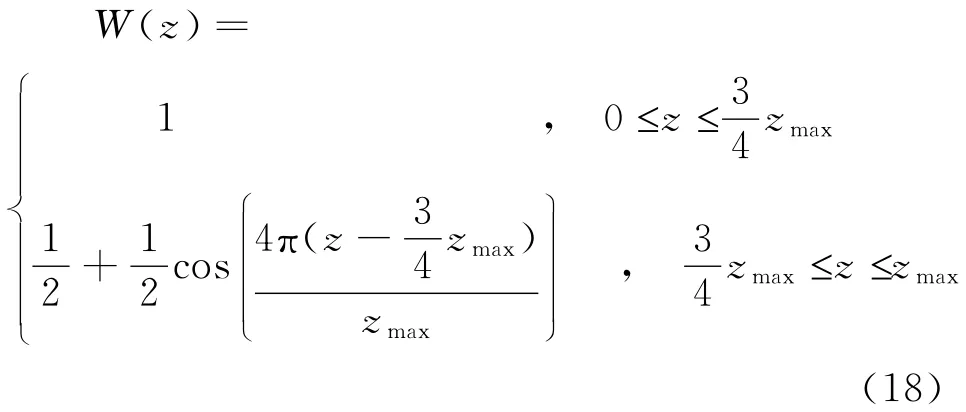
由于采用电磁场数值计算技术,必须考虑截断边界的影响.通过加窗函数的方法处理上边界,Cosine-taper窗函数形式如式(18)[10]:
式中:zmax为计算域的最大高度.
2.4 算法流程
与以往算法不同,笔者提出的算法除了在计算初始场时考虑了海面反射系数的影响,更重要的是在SSFT算法步进求解的过程中也考虑海面反射系数因素,如式(19)和图1所示.不同的边界条件影响均体现在反射系数参数中,从而可一致地计算导体、阻抗和粗糙面边界条件下的传播损耗.

计算流程如图1所示:
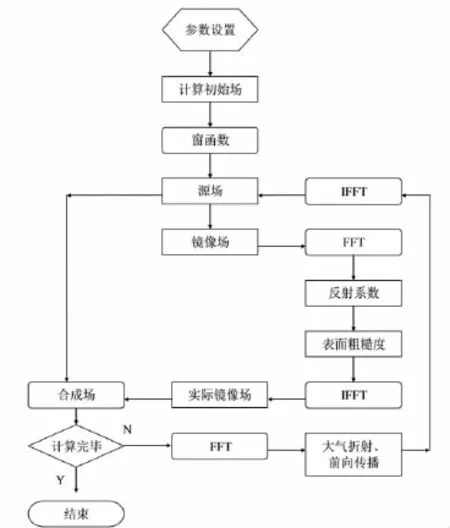
图1 海上抛物方程算法流程
3 仿真计算与比较
仿真计算海面蒸发波导环境中,在不同风速条件下,比较本算法与APM(Advanced Propagation Model)的预测结果.APM是美国的先进对流层折射效应预测系统(Advanced Refractive Effects Prediction System,AREPS)的核心计算模式,在包含大气波导的低高度区域内采用抛物方程模型,阻抗和粗糙边界条件下APM应用DMFT算法计算传播损耗[11].
仿真参数分别为:频率8 000GHz,极化方式水平极化,蒸发波导高度13.5m,天线高度10m,天线仰角0°,垂直半功率波束宽度3°,高斯性天线方向图.

图2 10m高度处两种算法的传播损耗随距离变化情况

图3 80km距离处两种算法的传播损耗随高度变化情况

图4 160km距离处两种算法的传播损耗随高度变化情况
图2 ~图4分别给出了不同风速条件下传播损耗计算结果.从图中可见,海面风速为0(光滑阻抗边界)和10m/s(粗糙边界)时,算法计算结果与APM模式计算结果都很一致.由图2可见,固定高度10m处,不同风速下,远距离区域内两种方法计算传播损耗差值在2dB以内;由图3和图4可知,以上仿真参数条件下,距离80km和160km处两种方法得到的传播损耗随高度变化也很一致,相差一般在3dB以内;蒸发波导高度内,两者结果相差小于2dB.以上结果表明了新算法的有效性.
4 结论
根据电波传播的角谱理论原理,基于SSFT算法研究在对流层大气波导环境下,在初始场和步进求解的过程中考虑不同边界面反射系数影响,得到了在大气波导环境下可一致计算水平或垂直极化波传播特性的新算法.通过仿真计算电波在蒸发波导、粗糙海面情况下的传播损耗,并把本文算法与APM的预测结果进行比较,两者结果基本一致.另外,该算法在各种条件下都能获得稳定解,表明了笔者的新算法具有普适性和有效性的特点.
[1]Leontovich M A,Fock V A.Solution of propagation of electromagnetic waves along the Earths’surface by the method of parabolic equations[J].J.Phys.USSR,1946,10(1):13-23.
[2]Hardin R H,Tappert F D.Application of the splitstep Fourier method to the numerical solution of nonlinear and variable coefficient wave equations[J].Society for Industry and Applied Mathematics Review,1973,15(2):423.
[3]Sirkova I,Mikhalev M.Parabolic Wave Equation Method Applied to the Tropospheric Ducting Propagation Problem:A Survey[J].Electromagnetics,2006,26(2):155-173.
[4]Kuttler J R,Dockery G D.Theoretical description of the parabolic approximation/Fourier split-step method of representing electromagnetic propagation in the troposphere[J].Radio Science,1991,26(2):381-393.
[5]Hitney H V.Modeling surface effects with the parabolic equation method[A].Hitney H V.Surface and Atmospheric Remote Sensing[C].San Diego:Geoscience and Remote Sensing Symposium,1994,4(1):2322-2325.
[6]Dockery D,Kuttler J R.An improved impedance boundary algorithm for Fourier split-step solutions of the parabolic wave equation[J].IEEE Transactions on Antennas and Propagation,1996,44(12):1592-1599.
[7]Guillet N,Fabbro V,Bourlier C,et al.Low grazing angle propagation above rough surface by the parabolic wave equation[A].Guillet N.Surface and Atmospheric Remote Sensing[C].San Diego:Geoscience and Remote Sensing Symposium,2003,7(7):4186-4188.
[8]Hannah B M.Modeling and Simulation of GPS Multipath Propagation[D].Brisbane:Queensland university of technology,2001.
[9]Kuttler J R,Janaswamy J.Improved Fourier transform methods for solving the parabolic wave equation[J].Radio Science,2002,37(2):1021-1031.
[10]Barrios A E.A terrain parabolic equation model for propagation in the troposphere[J].IEEE Transactions on Antennas and Propagation,1994,42(1):90-98.
[11]Barrios A E.Considerations in the development of the advanced propagation model(APM)for U.S.Navy applications[A].Barrios A E.Proceedings of the International Radar Conference[C].San Diego:Atmospheric Propagation Branch,2003:77-82.
Study of algorithm for atmospheric duct propagation with parabolic equation model over the sea
MENG Shusheng
(Department of Basic,Zhengzhou Institute of Science &Technology,Zhengzhou 450064,China)
According to the principle of the theory of angular spectrum of electromagnetic wave propagation,considering two kinds of polarized wave have different reflection coefficients on the conductor,impedance and rough surface boundary layer,adding the effect of reflection coefficients to the solving process of the initial field and the Split-step Fourier Transform solution,so the new algorithm which can be used to consistently calculate the propagation characteristics of horizontal or vertical polarization wave is obtained.The propagation loss is computed by this new algorithm in evaporation duct and rough sea surface condition.The performance of the new algorithm is then demonstrated with the result of other model.
atmospheric duct;parabolic equation;angular spectrum;boundary condition
TN011
A
1671-9476(2017)02-0066-04
10.13450/j.cnkij.zknu.2017.02.015
2016-08-24;
2016-10-18
国家高技术发展研究计划(863计划)“大气波导实施探测技术研究”(No.2008AA093001)
孟书生(1980-),男,河南正阳人,讲师,硕士,研究方向:海洋信息探测与处理.E-mail:mss0420@163.com,Tele:13592698724
