随机利率及O－U过程下的彩虹期权定价

石方圆，李翠香

（河北师范大学数学与信息科学学院，河北石家庄050024）

随机利率及O－U过程下的彩虹期权定价

石方圆，李翠香

（河北师范大学数学与信息科学学院，河北石家庄050024）

假设标的资产价格服从Ornstein－Uhlenback过程，利率r （t）服从Vasicek模型，利用保险精算方法给出了彩虹期权的定价公式，丰富了期权定价的理论.

Ornstein－Uhlenback过程；随机利率；彩虹期权；保险精算

近年来，随着全球金融市场的迅猛发展，期权在衍生证券中的地位显得尤为重要，其定价问题也是金融数学的核心问题之一，受到越来越多国内外学者的关注和研究.彩虹期权［1］是一种重要的新型金融衍生产品，它是讨论两个风险资产的最大值或最小值期权.资产最大值彩虹期权在到期日T的收益为

max｛ωmax［S1（T），S2（T）］－ωK，0｝，

资产最小值彩虹期权在到期日T的收益为

max｛ωmin［S1（T），S2（T）］－ωK，0｝，

其中ω＝±1.当ω＝1时为看涨期权，当ω＝－1时为看跌期权.

许多金融产品的定价可以利用彩虹期权的定价公式，例如外币期权、选择权债券和货币期权债券等等.因此对彩虹期权进行深入的研究与扩展有重要的意义.1982年，Stulz［2］在假设标的资产服从几何布朗运动以及利率、波动率为常数的条件下，研究了彩虹期权的定价公式.2011年，盛冠楠［3］在Stulz的基础上加入了跳扩散过程，得到了跳扩散模型下彩虹期权的定价公式.

在现实的金融市场中，股票的期望收益率不是随时间朝一个方向（上升或下降）变化的，资产的价格常常在上升到一定高度后有下降的趋势，应用O－U过程可以削弱上升的趋势.利率也不是一成不变的常数，在短时间内表现出一定的随机性，但长久来看，利率的变化有一定的均值回复性.这些在金融市场中都是十分常见的行为.因此，本文将在随机利率［4－5］的环境下，研究股票价格遵循指数O－U过程［4－6］的彩虹期权的定价公式.

另外，传统的定价方法通常假设金融市场是无套利、均衡、完备的，这与实际市场不太吻合.1998年Bladt和Rydberg［7］首次提出用保险精算方法给期权定价.该方法无任何经济假设，适用于有套利、非均衡、不完备的金融市场.之后许多学者利用此方法研究了期权的定价［8－10］.笔者将利用保险精算的方法给彩虹期权定价.

1 预备知识

定义1 随机过程Si（t）在时间［0，t］上产生的期望收益率ds定义为

定义2 执行价格为K，到期日为T的资产最大值彩虹期权和资产最小值彩虹期权在0时刻的保险精算价格定义分别为

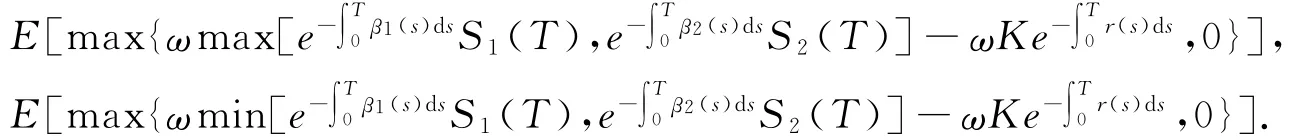
以下假设彩虹期权中两个资产价格及无风险利率r t（）分别服从如下随机微分方程（以后简称SDE）

其中B（t）＝（B1（t），…，Bn（t））为概率空间（Ω，T，｛t｝，P）上n维布朗运动，μi，αi，σij，m，a，σrj为常数.

引理1 假设资产价格Si（t）服从SDE（6），则有

证 由Ito公式可得

对上式两边从0到t积分并整理可得（8）.

由定义1及（8）可得

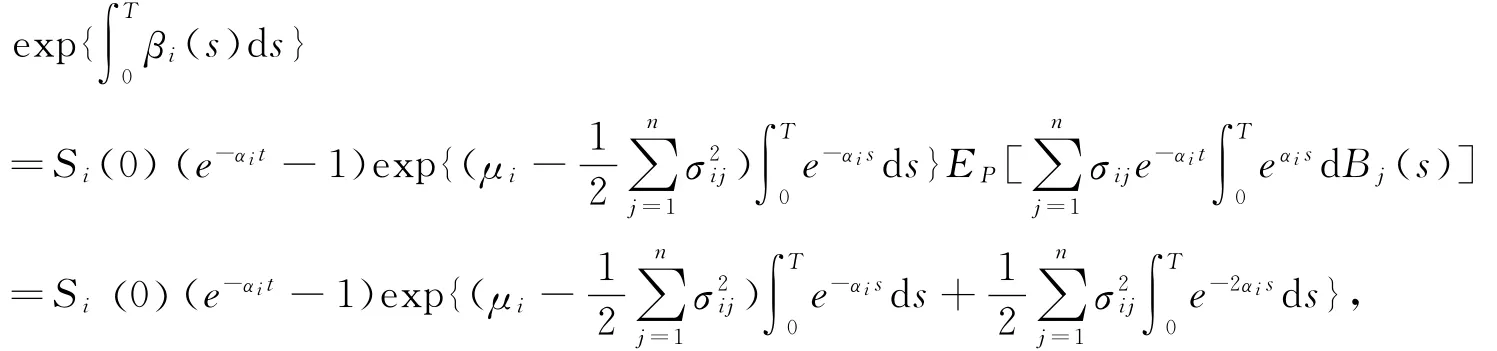
从而（9）式成立.

综上，引理1得证.

引理2 假设r t（）服从SDE（7），则有

证 由Ito公式可得

两边从0到t积分并整理可得

然后，从0到T积分可得

引理2得证.

引理3［11］设B（t）＝（B1（t），…，Bn（t））为测度P下n维布朗运动，H（t）＝（H1（t），…，Hn（t））为可料过程，且

则在Q下

引理4［11］设Λ（t）是正的P－鞅过程，且EP［Λ（T）］＝1.定义概率测度Q，使），则对任意随机变量X都有

2 彩虹期权的定价公式

下面来研究资产最大值彩虹看涨期权的保险精算定价.

定理1 假设Si（t）和r t（）分别服从SDE（6）和（7），则到期日为T，执行价格为K的资产最大值彩虹看涨期权在0时刻的保险精算价格为

故

证 因为

把这三项分别记作Π1，Π2，Π3，下面分别估计它们.

则Λ1（t）为正的P－鞅过程，且EP［Λ1（T）］＝1.定义概率测度Q1，使，则由引理4知

且由引理3知

是测度Q1下n个相互独立的布朗运动.

把式（11）代入式（9）中得

令

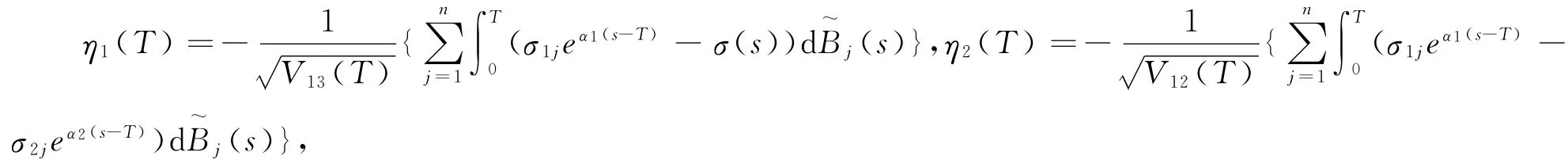
则（η1（T），η2（T））是相关系数为ρ1的二维正态分布.另外，由式（12）（13）（14）可得

故

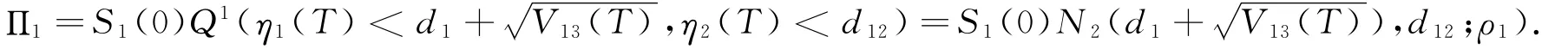
其次计算Π2.

令

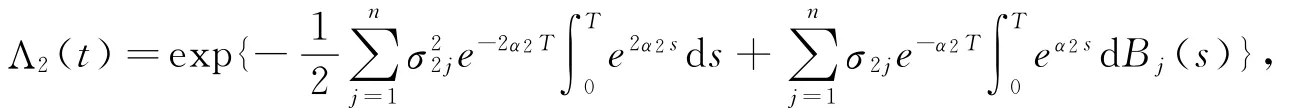
则Λ2（t）为正的P－鞅过程，且EP［Λ2（T）］＝1.定义概率测度Q2，使），则由引理4知

且由引理3知

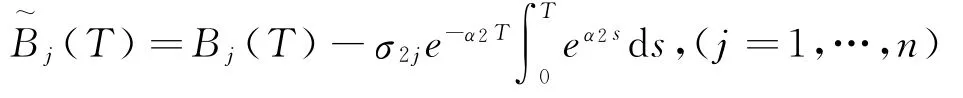
是测度Q2下n个相互独立的布朗运动.类似Π1的证明可得

最后计算Π3.

令

则Λ3（t）为正的P－鞅过程，且EP［Λ3（T）］＝1.定义概率测度Q3，使，则由引理4知

且由引理3知

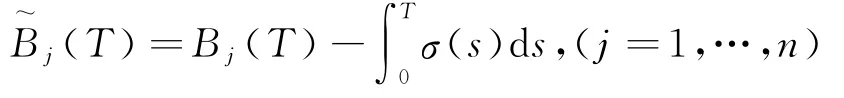
是测度Q3下n个相互独立的布朗运动.类似Π1的证明可得

Π3＝Ke－D（T）［1－N2（－d1，－d2；ρ3）］.

综上，定理1得证.同理可证以下三个定理.

定理2 假设Si（t）和r t（）分别服从SDE（6）和（7），则到期日为T，执行价格为K的资产最大值彩虹看跌期权在0时刻的期权价值为

定理3 假设Si（t）和r t（）分别服从SDE（6）和（7），则到期日为T，执行价格为K的资产最小值彩虹看涨期权在0时刻的期权价值为

定理4 假设Si（t）和r t（）分别服从SDE（6）和（7），则到期日为T，执行价格为K的资产最小值彩虹看跌期权在0时刻的期权价值为

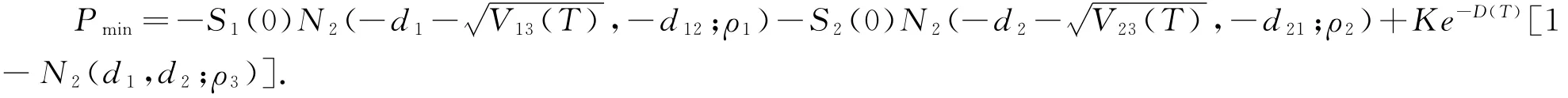
3 结束语

对新型期权进行合理定价已经成为金融数学研究的重要内容之一.至今为止，很多专家学者取得了丰硕的研究成果.笔者在这些研究的基础上，在O－U过程下考虑资产收益率的均值回复性和利率的随机性对期权价格的影响，用保险精算方法给出了彩虹期权定价公式.得到的期权定价公式扩展了文献［1］中的结论，而且笔者结论还可以进一步扩展至多资产最优或最差选择期权的定价.

［1］Zhang P G.Exotic options［M］.北京：机械工业出版社，2014：312－315.

［2］Stulz R M.Options on the minimum or maximum of two risky assets［J］.Journal of Financial Economics，1982，10（2）：161－185.

［3］盛冠楠.跳扩散模型下极值期权的定价［D］.广西：广西师范大学，2011.

［4］刘坚，文凤华.欧式期权和交换期权在随机利率及O－U过程下的精算定价方法［J］.系统工程理论与实践，2009，29（12）：13－15.

［5］赵攀，肖庆宪.随机利率下O－U过程的幂型欧式期权定价［J］.合肥工业大学学报（自然科学版），2014，37（11）：1386－1390.

［6］刘兆鹏，刘钢.基于O－U过程具有不确定执行价格的期权保险精算定价［J］.杭州师范大学学报（自然科学版），2011，10（4）：316－319.

［7］M Bladt，H T Rydberg.An actuarial approach to option pricing under the physical measure and without market assumptions［J］.Insurance Mathematics and Economics，1998，22（1）：65–73.

［8］严海峰，刘三阳.广义Black－Scholes模型期权定价新方法——保险精算方法［J］.应用数学与力学，2003，24（7）：730－738.

［9］郑红，郭亚军.保险精算方法在期权定价模型中的应用［J］.东北大学学报（自然科学版），2008，29（3）：429－432.

［10］毕学慧，杜雪樵.复合期权的保险精算定价［J］.合肥工业大学学报（自然科学版），2008，31（8）：43－47.

［11］Fima C Klebaner.Introduction to stochastic calculus with applications［M］.北京：人民邮电出版社，2008.

Pricing of rainbow options under Ornstein-Uhlenback process and stochastic rate

SHI Fangyuan，LI Cuixiang
（College of Mathematics and Information Science，Hebei Normal University，Shijiazhuang 050024，China）

In this paper，we suppose that the underlying asset price process follow the Ornstein-Uhlenback process，the riskless interest r （t）submit to Vasicek model.The pricing of rainbow options is given by using an actuarial approach.These results enrich the theory of option pricing.

OrnsteinUhlenback process；stochastic interest rate；rainbow option；actuarial approach

O211.6

A

1671-9476（2017）02-0001-06

10.13450／j.cnkij.zknu.2017.02.001

2016-10-18；

2016-11-11

国家自然科学基金（No.11571089）

石方圆（1991－），女，河北邢台人，硕士研究生，研究方向：金融工程与风险管理.