我国玉米价格波动的短期预测——基于X-12-ARIMA的实证分析

杨世娟，徐慧芳

（黄山学院 数学与统计学院，安徽 黄山 245021）

我国玉米价格波动的短期预测
——基于X-12-ARIMA的实证分析

杨世娟，徐慧芳

（黄山学院 数学与统计学院，安徽 黄山 245021）

利用X-12方法对我国玉米价格序列进行季节调整，对消除季节因素的价格序列建立ARIMA（4，1，0）模型进行分析。结果发现，我国玉米价格季节性波动呈逐年减弱趋势，前期价格波动、外部其他因素的干扰都会持续影响后期价格的变化。同时，玉米交易市场不会出现“高风险、高回报”现象。最后，利用该模型对玉米价格进行预测。

季节调整；X-12-ARIMA；玉米价格

随着国际市场粮价的大幅度震荡、国内地价的不断上涨，使得国内粮食生产成本不断提高，这直接影响了我国经济主体运行的稳定及人民生活水平的提高。例如，我国玉米价格的上涨，在2005—2014年的十年间，涨幅最高达到137%。我国玉米价格的较大幅度上涨是从2006年12月开始的，在之后的几个月，玉米价格上涨幅度达到26%，价格处于高位。近二年，2009年1月价格开始下跌，跌幅近20%，两个月后，在2009年3月至今玉米价格持续走高，并缓慢上升（数据来源于《中国农产品价格调查年鉴（2005—2014年）》）。玉米价格的波动对种植玉米的农民、收售玉米的商贩都造成很大的干扰，同时会引发整个社会物价水平的波动。

粮食价格调控一直是我国十分关注的问题，涉及广大群众对民生生活幸福指数的评价。吕捷、林宇洁研究了国际玉米价格波动的特征及其国际玉米价格对我国玉米市场安全的影响[1]。于左等对我国玉米价格缺失竞争力的形成机制进行了研究并给出合理的建议，进一步采取相关措施来减少缺乏竞争力对我国玉米价格波动的影响[2]。国内诸多学者对玉米价格波动的研究也已经不再局限在描述性统计[3～5]。随着经济全球化进程的不断加快，取消关税后国内与国际市场的联系日益紧密，如何有效利用国际玉米市场保障国内玉米市场稳定。在此背景下，对我国玉米价格波动情况进行研究具有实际意义。

一、X-12-ARIMA模型

（一）X-12方法介绍

X-12方法是基于移动平均的季节调整方法，季节调整经常用到的两种方法分别是加法模型和乘法模型。

1.加法模型的一般形式为：Yt=Tt+St+Ct+It。

2.乘法模型的一般形式为：Yt=Tt×St×Ct×It。

其中，Tt、St、Ct、It分别表示长期趋势、季节变动、周期变动、不规则变动因素。相对而言，乘法模型应用得更加广泛。

（二）ARIMA模型介绍

ARIMA（p，d，q）模型包含三种情况，AR（p）、MA（q）或者ARMA（p，q），若原序列是单证的非平稳序列，则对差分后的序列建立上述三种模型[6]。

1.ARIMA（p，d，q）模型的表达形式

AR（p）模型对应的代数表达式为：yt=c+α1yt-1+α2yt-2+…+ αpyt-p+εt。

MA（q）模型对应的代数表达式为：yt=c+εt+θ1εt-1+θ2εt-2+…+ θqεt-q。

ARMA（p，q）模型对应的代数表达式为：yt=c+α1yt-1+α2yt-2+ …+αpyt-p+εt+θ1εt-1+θ2εt-2+…+θqεt-q。

2.ARIMA（p，d，q）模型的识别

（1）d参数的识别。对分析的原序列进行单位根检验，若有单位根的，通过差分后的序列进行判断，如果d阶差分后的序列是平稳的，则此时序列为d阶单整序列，即参数d被识别。

（2）p、q的识别。主要依据偏自相关函数与自相关函数进行识别，具体参照进行判断。

二、实证分析

（一）数据来源

选取2005年1月至2014年12月共120个玉米价格数据作为样本，记作ym，对其进行实证分析，首先，ym对数据进行图形分析（如图1所示）。

从图1可以看出，玉米价格具有趋势性和季节性，采用X-12-ARIMA方法进行季节调整。

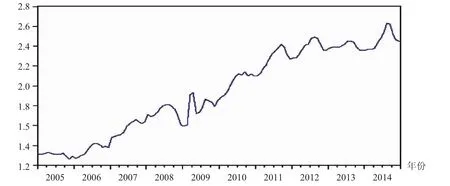
图1 玉米价格ym序列图

（二）玉米价格的季节性波动特征

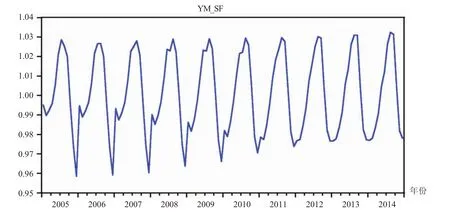
图2 2005—2014年玉米价格季节波动图

X-12-ARIMA季节调整模型分析时选择乘法形式。在2015—2014的十年间，玉米价格的季节性指数年极差值呈逐年递减趋势，由2005年的7.02%降至2014年的5.54%，表明玉米价格季节波动呈持续减弱的趋势。从图2可以看出，2005年玉米价格波动的波峰为7月，而从2006年开始波动的波峰退后到了8月，同时每年2月会出现一个小幅度的回升。波谷为每年的12月，且相对稳定。从而可以总结出，我国玉米价格季节波动具有如下特点：第三季度价格波动值最大，处于全年最高值，之后逐步降低，第四季度达到全年价格的最低值，然后以周期形式反复。

序列ym季节性统计量检验值P=0.46＜1，体现季节调整效果较好。季节的稳定性检验结果P＜0.05（F=12.818），表明我国玉米价格序列存在稳定的季节性。

（三）季节调整后序列的波动分析

1.平稳性检验。文中研究数据选取的是时间序列数据，对此需要进行平稳性检验，首先，把原序列进行季节性消除，消除季节性的序列简记为TC。消除季节性之后，序列TC总体呈上升趋势，明显不平稳，为了对序列的研究结果更可信，对序列TC进行平稳性检验。利用单位根检验法（检验形式包括常数项和时间趋势项）进行分析（见表1）。

TC序列的单位根检验P值为0.3629＞0.05，不能够拒绝原假设，说明TC序列存在单位根，即序列为不平稳序列。对此，将序列TC进行差分，记作DTC，对序列DTC进行单位根检 验（如表2所示）。

表1 序列TC单位根检验

表2 序列DTC单位根检验

序列DTC的单位根检验P值为0.0484＜0.05，拒绝原假设，说明序列DTC不存在单位根，此时序列为非白噪声的平稳序列，可以建立ARIMA模型，直至残差序列通过白噪声检验，最终利用建立的模型对玉米价格做近期预测。

2.ARIMA模型的建立。在ARIMA（p，d，q）模型在阶数选择上，由于对原序列TC进行一次差分之后，序列DTC已经平稳，故d=1。下面对p，q进行确定（如图3所示）。

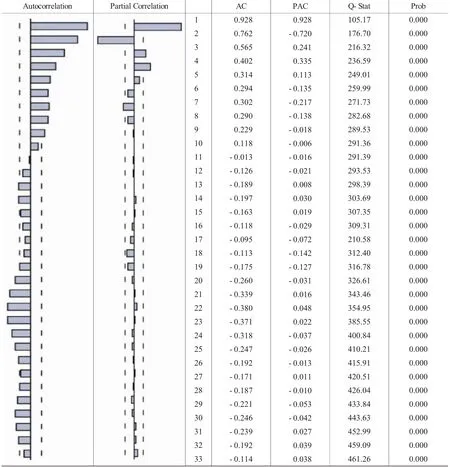
图3 序列DTC的自相关与偏自相关图

从图3可以推断出模型中的p=3，或p=4，其中q=0；进而对序列DTC建立ARIMA（3，1，0）和ARIMA（4，1，0）模型 进行分析（如表3和表4所示）。

表3 ARIMA（3，1，0）模型结果

表4 ARIMA（4，1，0）模型结果

从表3和表4中不难发现，模型各个系数均通过检验，但是具体对模型的选择上，从模型的拟合优度进行选择（见表5），对此选择ARIMA（4，1，0）模型进行拟合与预测。

运用该模型对2005—2014年的时间序列DTC进行拟合（见图4），并通过计算，求出ARIMA模型拟合后的玉米价 格，并给出与原玉米价格比较的对比图、残差图（见图5），从图中也明显地看出建立的模型拟合度比较高。从计算的角度而言，通过求得2014年玉米价格的平均绝对误差为8.32%，更加表明该模型的拟合效果较好。

表5 模型对比分析

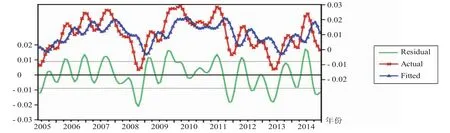
图4 拟合序列DTCF与原序列DTC对比图

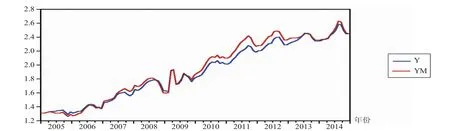
图5 拟合玉米价格与原价格对比图

三、结论与建议

通过X-12-ARIMA模型对我国玉米价格走势进行分析，得到玉米价格季节波动呈现逐年递减的趋势。玉米价格虽然不断上涨，但上涨趋势呈现越发平稳状态。而且库存对玉米价格的影响具有较大作用，由此，我国需要合理控制库存，保证总体供给与需要的合理关系。同时，我国玉米市场存在明显的波动性，玉米价格大的波动往往连续出现。前期玉米价格波动和外部冲击对价格走势的影响具有持续性。通过模型建立发现，我国玉米市场若出现“高风险、高回报”特征是不现实的。今后，我们需要及时关注玉米价格上涨的动态变化信息，以防价格的不良波动给广大人民生活带来不良的影响。

[1]吕捷，林宇洁.国际玉米价格波动特性及其对中国粮食安全影响[J].管理世界，2013，(5)：76-87.

[2]于左，高建凯.中国玉米价格竞争力缺失的形成机制与政策[J].农业经济问题，2013，(8)：10.

[3]李剑，宋长鸣，项朝阳.中国粮食价格波动特征研究——基于X-12-ARIMA模型和ARCH模型[J].统计与信息论坛，2013，(6)：16-20.

[4]桂文林，韩兆洲.基于X-12-ARIMA模型的中国粮食消费价格运行[J].华东经济管理，2011，(3)：61-67.

[5]苗珊珊.中国粮食价格波动的农户福利效应研究[J].资源科学，2014，(2)：370-378.

[6]李嫣怡，等.Eviews统计分析与应用[M].北京：电子工业出版社，2014：153-161.

[责任编辑 刘娇娇]

F323.7

A

1673-291X（2017）21-0005-05

2017-02-07

安徽省教育厅自然科学研究项目（KJHS2016B04）；黄山学院自然科学研究项目（2015XKJ004）；大学生创新创业训练项目（201510375019）

杨世娟（1988-），女，安徽安庆人，教师，硕士，从事应用统计研究。