5d过渡金属原子掺杂六方氮化铝单层的磁性及自旋轨道耦合效应:可能存在的二维长程磁有序∗

杨明宇 杨倩 张勃张旭 蔡颂 薛玉龙 周铁戈

(南开大学电子信息与光学工程学院,天津 300350)

(2016年11月27日收到;2016年12月28日收到修改稿)

5d过渡金属原子掺杂六方氮化铝单层的磁性及自旋轨道耦合效应:可能存在的二维长程磁有序∗

杨明宇 杨倩 张勃†张旭 蔡颂 薛玉龙 周铁戈

(南开大学电子信息与光学工程学院,天津 300350)

(2016年11月27日收到;2016年12月28日收到修改稿)

采用基于密度泛函理论的第一性原理计算方法,研究了5d过渡金属原子(H f,Ta,W,Re,Os,Ir,Pt, Au和Hg)取代六方氮化铝单层中的A l原子的几何结构、电子结构、磁性性质、铁磁态与反铁磁态能量差(EFM−EAFM)以及自旋轨道耦合效应导致的磁各向异性.研究发现Hg掺杂的体系中,5d金属原子和最邻近的N原子的键长最大,平均值为2.093Å,之后依次是Au,H f,Pt,Ta和Ir.态密度结果显示掺杂体系的禁带中出现明显的杂质能级,给出了掺杂体系的总磁矩以及自旋密度的分布.对于EFM−EAFM,Hf,Re,Pt和Au四种原子的掺杂在4×8超胞中到达最大值,分别为−187.2563,286.2320,−48.0637和−61.7889meV.磁各向异性结果中,Re掺杂的磁各向异性最大,达到11.622 meV.结合以上结果,我们预测5d过渡金属原子掺杂六方氮化铝单层可能存在二维长程磁有序.

六方氮化铝单层,第一性原理计算,密度泛函理论,自旋轨道耦合效应

1 引 言

二维纳米材料[1−4]在纳米电子学[5,6]和自旋电子学[7−9]中都有很好的应用前景,因此针对二维纳米材料的研究备受关注.为满足二维材料在实际应用中的各种需要,对它们的电子结构、磁性性质的调制尤为重要[10−12].二维材料的磁性研究是重要的课题,磁各向异性决定了材料的磁稳定性,对磁各向异性的研究有助于揭示其物理起源,为更好地满足人们对磁各向异性材料的需求创造条件.遗憾的是,大多数现有的二维材料都没有预期的磁有序.因为按照M erm in-Wagner定理,在零摄氏度以上的二维体系中,各向同性海森伯模型不能拥有长程磁有序[13].然而,磁各向异性[14,15]可以产生一个长波长的自旋波能隙来去除M erm in-Wagner定理的限制[16],进而产生长程磁有序.

5d过渡金属原子具有很强的自旋轨道耦合效应[17−19],能够产生强磁各向异性,吸附于低维体系后可能制备出优质的自旋材料器件,目前越来越受重视[20].2009年,Shitade等[21]报道了5d过渡金属氧化物Na2IrO3中存在自旋霍尔效应[22,23]. 2012年,Zhang等[24]报道了5d原子吸附于石墨烯时发生量子反常霍尔效应,Hu等[25]报道了5d原子吸附于石墨烯时出现拓扑绝缘体能隙.我们对5d原子掺杂二维体系进行了系统研究.考虑到稀磁半导体(diluted magnetic sem iconductor, DMS)[26−28]同时具有半导体性质和铁磁性质,是当今半导体领域的研究热点,而氮化铝(A lN)作为新型的III-V族稀磁半导体中带隙最宽的半导体,在掺杂低维体系和III-V族化合物的新型材料中备受瞩目,在光学、电学、磁学等多个方向有很可观的应用前景.并且由于实验的局限性,关于A lN单层理论方面的研究十分必要.本文采用基于密度泛函理论的第一性原理计算方法,研究了5d过渡金属原子取代六方氮化铝单层中的A l原子的几何结构、电子结构、磁性性质、铁磁态(ferromagnetic, FM)与反铁磁态(antiferromagnetic,AFM)能量差(EFM−EAFM)以及自旋轨道耦合效应导致的磁各向异性,并首次预测其中可能存在二维长程磁有序.

2 模型和计算方法

六方氮化铝单层的原胞中含有1个A l原子和1个N原子,我们分别构建2×2,3×3,4×4和5×5的A lN超胞.计算中,用一个5d原子取代超胞中的一个A l原子.掺杂后,2×2,3×3,4×4和5×5超胞的掺杂浓度依次是12.5%,5.556%,3.125%和2%.图1给出5d原子取代A lN中A l的几何结构.

图1 (网刊彩色)5d原子取代A lN单层中A l原子的几何结构 (a)2×2超胞;(b)3×3超胞;(c)4×4超胞; (d)5×5超胞;粉色球、蓝色球和粉蓝色球分别表示A l, N和5d原子Fig.1.(color on line)Geom etric structures of 5d atom s doped A lN m onolayers:(a)2×2 supercell;(b)3×3 supercell;(c)4×4 supercell;(d)5×5 supercell;p ink, b lue and pow der b lue balls stand for A l,N and 5d atom s,respectively.

使用ABINIT[29,30]对掺杂体系的几何结构、电子结构和磁性性质进行计算,计算过程分为两步:首先,针对已经构建的模型进行结构优化,进而得到稳定的几何结构;然后,对优化后体系的电子结构、磁性性质以及磁各向异性进行高精度计算.采用投影缀加波方法[31]描述电子与离子实之间的相互作用,采用广义梯度近似[32]描述电子间的交换关联相互作用,采用平面波展开价电子波函数.综合考虑到计算精度和计算代价,设置平面波的截断能为400 eV.2×2超胞选用5×5×1的k点网格, 3×3超胞选用4×4×1的k点网格,4×4超胞选用3×3×1的k点网格,5×5超胞选用2×2×1的k点网格.在几何结构优化中,能量收敛标准设定为1×10−4eV,当原子受力小于0.02 eV/Å停止晶格优化.在电子结构和磁性性质计算中能量收敛标准设定为1×10−5eV.对总磁矩不为0的体系进行铁磁态-反铁磁态能量差的计算,计算时将超胞扩大为原来两倍.原来的2×2,3×3,4×4和5×5超胞分别变为2×4,3×6,4×8和5×10的超胞.掺杂原子变为2个,初始磁矩分别设定为同向和反向并计算总能量,能量收敛标准设定为1×10−5eV.计算磁各向异性时,考虑到计算代价,只对5d原子掺杂的4×4超胞进行计算,加入自旋轨道耦合效应,能量收敛标准设定为1×10−7eV.分别设定电子自旋方向为垂直和平行于A lN平面方向,然后自洽计算体系的总能量.

3 计算结果与讨论

3.1 几何结构

表1列出了几何结构优化后得到的5d金属原子掺杂2×2,3×3,4×4和5×5超胞中5d原子到最近邻的N原子的键长h.

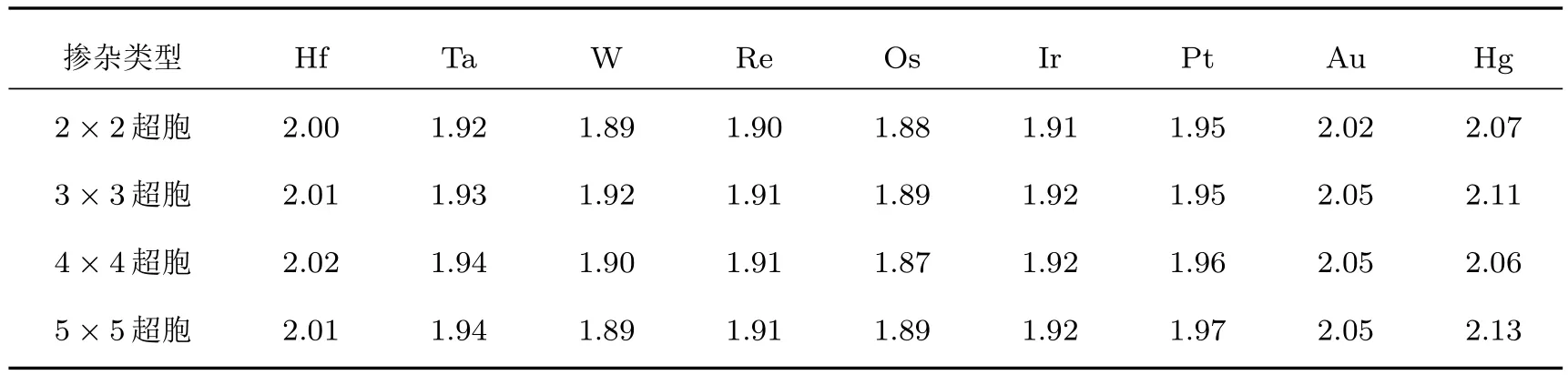
表1 5d原子和最近邻的N原子的键长h(Å)Tab le 1.Bond lengths between 5d atom s and the nearest neighbor N atom s h(Å).

过渡金属原子具有局域对称性,到最近邻的3个N原子的距离近似相等.键长h有如下规律.首先,对于同样大小的超胞,Hg掺杂时h最大,平均值为2.09Å;之后依次是Au,H f,Pt,Ta和Ir,平均值分别为2.04,2.01,1.96,1.93和1.92Å.对于Re, W和Os掺杂,h随着超胞的变化略有调整,但都在1.89Å上下浮动.从整体上来讲,5d金属原子掺杂的超胞h在1.874—2.127Å范围之间.其次,对于同一种5d金属原子,掺杂2×2,3×3,4×4和5×5超胞对h的影响不大.

3.2 电子结构

图2和图3分别给出了H f,Ta,W,Re,Os,Ir, Pt,Au和Hg掺杂2×2超胞和5×5超胞的总态密度,其中虚线表示费米能级.

掺杂体系的禁带中出现明显的杂质能级,对比图2和图3可以看出,当超胞减小(掺杂浓度增加)时,杂质能级明显展宽.以Ir为例,当采用5×5的超胞时,费米能级处态密度为0,为绝缘体.而采用2×2超胞时,由于能级展宽,费米能级处态密度不为零,变为金属.由从图2给出的2×2超胞的结果中可以看出,对于Ta,Ir,Pt,Au和Hg掺杂的情况,总态密度呈现对称性,体系无磁性;对于H f,W,Re和Os掺杂的情况,总态密度呈现不对称性,体系有磁性.W和Os掺杂时体系更是呈现出半金属特性,这在自旋电子器件中具有重要意义.5d金属原子掺杂5×5超胞的总态密度和5d金属原子掺杂3×3和4×4超胞的总态密度情况相似,对于Ta和Ir掺杂,总态密度对称,体系无磁性;对于H f,W, Re,Os,Pt,Au和Hg掺杂,总态密度不对称,体系有磁性.

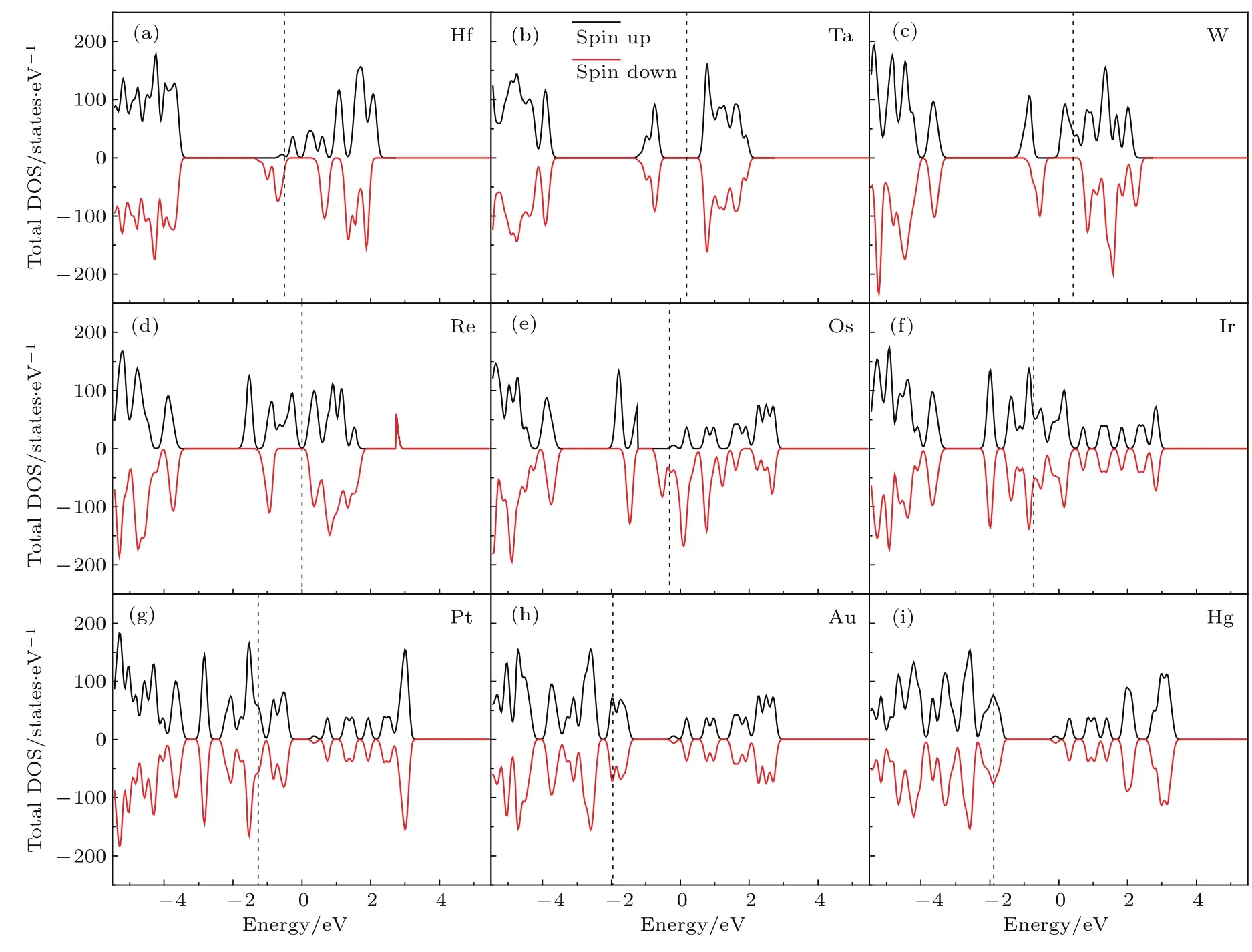
图2 (网刊彩色)5d原子取代2×2超胞A l原子的总态密度 (a)H f;(b)Ta;(c)W;(d)Re;(e)Os;(f)Ir; (g)Pt;(h)Au;(i)HgFig.2.(color on line)Total density of states(DOS)of 5d atom s doped 2×2 supercells:(a)H f;(b)Ta; (c)W;(d)Re;(e)Os;(f)Ir;(g)Pt;(h)Au;(i)Hg.

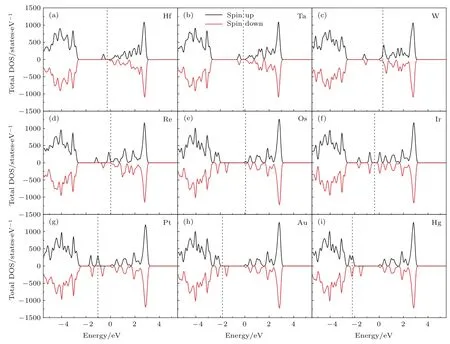
图3 (网刊彩色)5d原子取代5×5超胞A l原子的总态密度 (a)H f;(b)Ta;(c)W;(d)Re;(e)Os;(f)Ir; (g)Pt;(h)Au;(i)HgFig.3.(color on line)Total DOS of 5d atom s doped 5×5 supercells:(a)H f;(b)Ta;(c)W;(d)Re;(e)Os; (f)Ir;(g)Pt;(h)Au;(i)Hg.

3.3 磁性性质

3.3.1 体系的总磁矩

5d原子掺杂2×2,3×3,4×4和5×5超胞的总磁矩Mtotal如表2所列.

由于5d原子的价电子排布与原子序数有关,导致不同的掺杂体系总磁矩不同.由表2可以看出:Ta,Ir掺杂的2×2,3×3,4×4和5×5超胞的总磁矩均为0;Pt,Au和Hg掺杂2×2超胞的总磁矩均为0;而Pt,Au和Hg掺杂3×3,4×4,5×5超胞时,均有磁矩产生,其中Pt和Hg掺杂的总磁矩近似为1µB,Au掺杂的总磁矩为2µB,Au掺杂的总磁矩是这个掺杂体系总磁矩的最大值.这说明对于Pt,Au和Hg这三种元素的掺杂而言,掺杂浓度的变化对掺杂后体系的总磁矩有较大的影响,当掺杂浓度由12.5%降低到5.556%,3.125%和2%时,有磁矩产生;Hf掺杂和Re掺杂体系的总磁矩与掺杂浓度关系不大,H f掺杂体系的总磁矩随掺杂浓度的降低从0.932µB缓慢增长到1µB,Re掺杂体系的总磁矩随掺杂浓度的升高从1.986µB缓慢增长到2µB;W掺杂2×2,3×3,4×4和5×5超胞的总磁矩分别为1µB,0.869µB,0.479µB和0.388µB,变化非常明显,最大值是最小值的2.56倍.这表明,W掺杂体系的总磁矩与掺杂浓度有很大关系,掺杂浓度越小,掺杂体系的总磁矩越小; Os掺杂2×2,3×3,4×4和5×5超胞的总磁矩,随掺杂浓度的变化趋势不一致,呈现出先减小再增大的趋势.对于Os掺杂2×2超胞,当掺杂浓度为12.5%时,掺杂体系的总磁矩达到最大值1.409µB;对于Os掺杂3×3超胞,当掺杂浓度降低到5.556%时,掺杂体系的总磁矩最小为1.005µB;其余总磁矩分别为1.075µB和1.169µB.

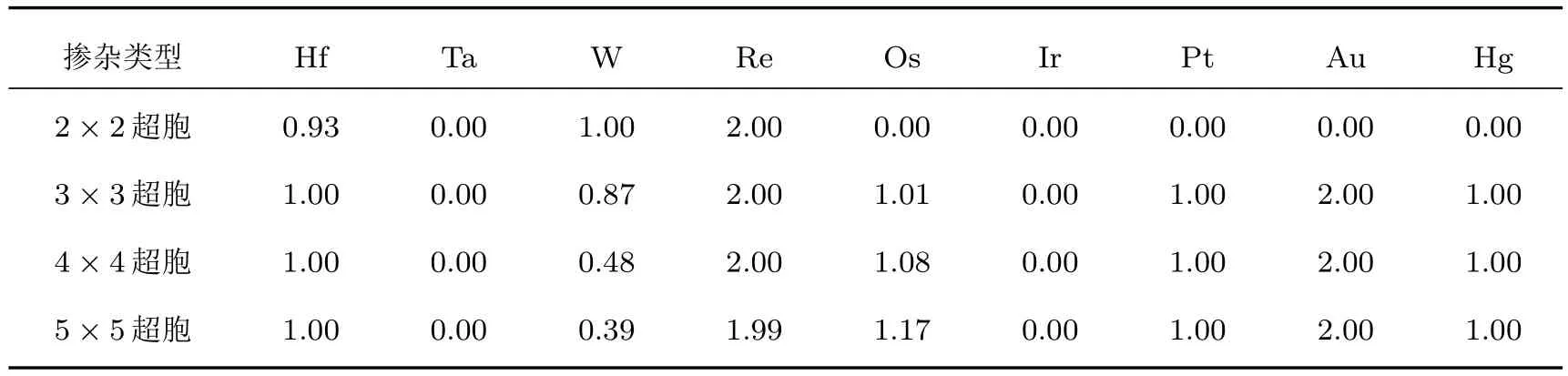
表2 5d原子掺杂2×2,3×3,4×4,5×5超胞的总磁矩Mtotal/µBTab le 2.Totalm agnetic m om ents(Mtotal/µB)of 5d atom s doped 2×2,3×3,4×4,and 5×5 supercells.

3.3.2 自旋密度

从自旋密度图可以直观地看出体系的磁矩分布情况.图4给出的是5d原子掺杂5×5超胞(掺杂浓度为2%)时得到的自旋密度,可以看出对于同一种超胞大小,磁矩主要集中在5d原子附近,以自旋向上的磁矩为主.其中Ta和Ir掺杂的5×5超胞的总磁矩为零.

为了研究在同一种5d金属原子掺杂下不同掺杂浓度对体系磁矩分布的影响,图5分别给出了Hf掺杂时的自旋密度,其中包含2×2,3×3和4×4三种超胞.可以看出,H f掺杂后体系的磁矩分布,在不同超胞大小情况下也与5×5超胞情况一致,主要集中在杂质原子附近,在A lN单层的其他空间内几乎没有磁矩的分布.对于Au,W,Re,Os,Pt和Hg掺杂后的体系而言,磁矩的分布与掺杂浓度变化不大,都集中分布在杂质原子附近.

3.3.3 铁磁态-反铁磁态能量差

计算铁磁态能量时,设置掺杂体系中相邻两个5d杂质原子自旋方向均向上;计算反铁磁态能量时,相邻两个5d杂质原子自旋方向一个向上,一个向下.以Re掺杂为例,图6给出了计算得到的不同超胞铁磁态和反铁磁态的自旋密度,其中图6(a)—(d)分别为2×4,3×6,4×8和5×10超胞铁磁态,图6(e)—(h)为对应的反铁磁态.

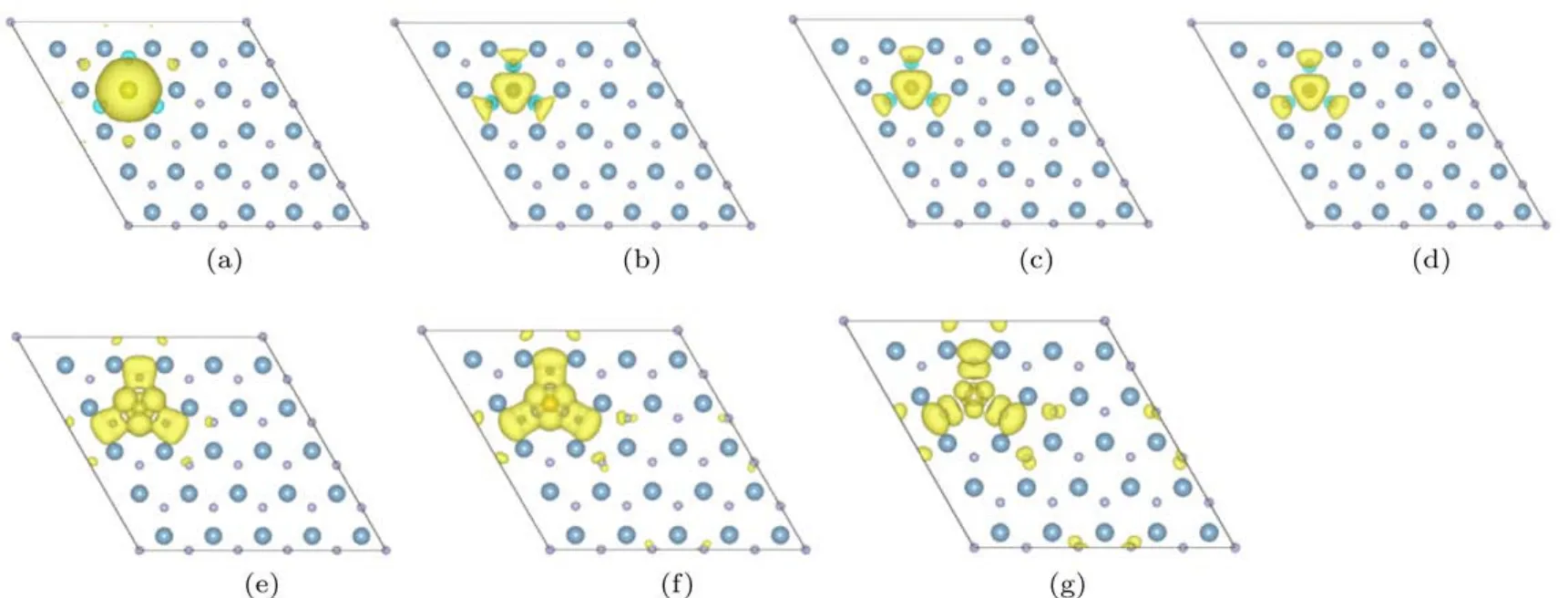
图4 (网刊彩色)5d原子取代5×5超胞A l原子的自旋密度图 (a)H f;(b)W;(c)Re;(d)Os;(e)Pt;(f)Au; (g)Hg;黄色和青色分别代表自旋向上和自旋向下(下同)Fig.4.(color on line)Sp in density m aps of 5d atom s doped 5×5 supercells:(a)H f;(b)W;(c)Re;(d)Os; (e)Pt;(f)Au;(g)Hg;yellow and cyan stand for up-sp in and dow n-sp in,respectively(the sam e below).

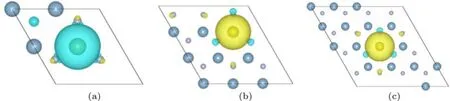
图5 (网刊彩色)H f原子取代A l原子后体系自旋密度图 (a)2×2超胞;(b)3×3超胞;(c)4×4超胞Fig.5.(color on line)Sp in density m aps of H f doped A lN m onolayers:(a)2×2 supercell;(b)3×3 supercell; (c)4×4 supercell.

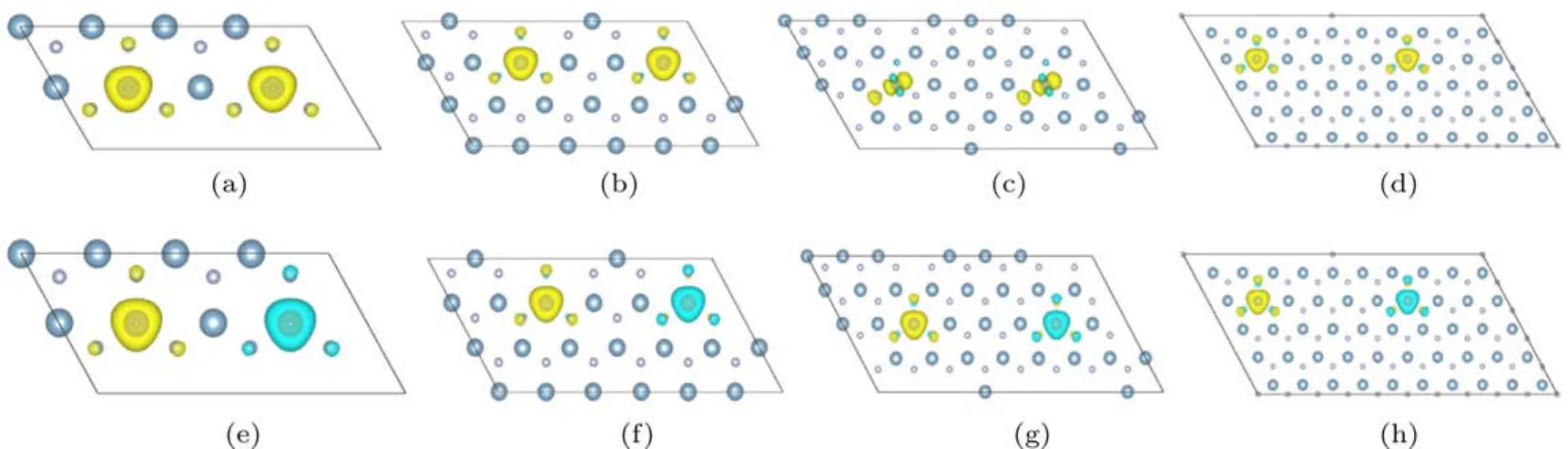
图6 (网刊彩色)Re原子取代A l原子后体系自旋密度图 (a)2×4超胞铁磁态;(b)3×6超胞铁磁态;(c)4×8超胞铁磁态;(d)5×10超胞铁磁态;(e)2×4超胞反铁磁态;(f)3×6超胞反铁磁态;(g)4×8超胞反铁磁态; (h)5×10超胞反铁磁态Fig.6.(color on line)Spin density m aps of Re atom doped A lN m onolayers:(a)FM of 2×4 supercell; (b)FM of 3×6 supercell;(c)FM of 4×8 supercell;(d)FM of 5×10 supercell;(e)AFM of 2×4 supercell; (f)AFM of 3×6 supercell;(g)AFM of 4×8 supercell;(h)AFM of 5×10 supercell.

表3列出了计算得到5d过渡金属原子掺杂2×4,3×6,4×8和5×10超胞的铁磁态-反铁磁能量差(EFM−EAFM).

由表3可以看出:Hf,Re,Pt和Au四种原子的掺杂在4×8超胞中EFM−EAFM到达最大值,分别为−187.2563,286.2320,−48.0637和−61.7889meV,Hg掺杂在3×6超胞EFM−EAFM达到最大值−20.4487 meV,W和Os掺杂在2×4超胞中EFM−EAFM最大,分别为−45.8162和−43.7026meV;其次,Hf掺杂在3×6超胞和5×10超胞,Re掺杂在3×6超胞、4×8超胞和5×10超胞,Pt掺杂在3×6超胞,Au掺杂在5×10超胞,Hg掺杂在4×8超胞,EFM−EAFM为正数,铁磁态大于反铁磁态,说明反铁磁态更稳定;Hg和W掺杂在5×10超胞中能量差近似为0,说明铁磁态和反铁磁态稳定性近似相同;其他情况下,EFM−EAFM为负数,铁磁态小于反铁磁态,说明铁磁态更稳定.

3.3.4 磁各向异性

表4列出了垂直于平面方向(z轴方向)与平行于平面方向(x轴方向)的能量差,其中Ta掺杂和Ir掺杂总磁矩为0.

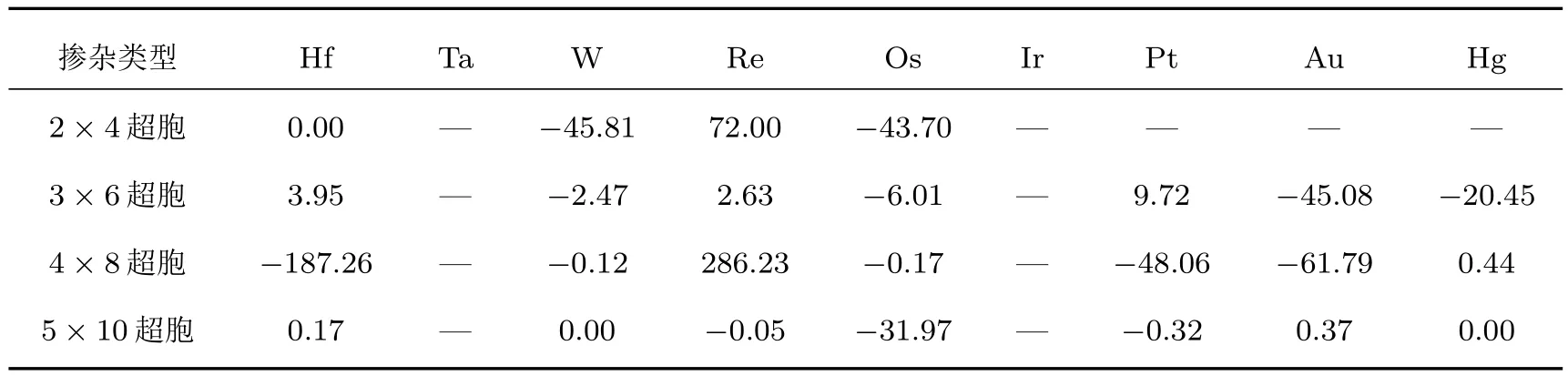
表3 5d原子掺杂各超胞铁磁态反铁磁态能量差EFM−EAFM(m eV)Table 3.The energy diff erences between FM and AFM states EFM−EAFM(m eV).

表4 5d原子掺杂4×4超胞磁各向异性能Tab le 4.M agnetic anisotropy energies of 5d atom s doped w ith 4×4 supercells.

由表4可以看出,5d原子掺杂4×4超胞磁各向异性可以分为两类.第一类是磁各向异性为正值, Re掺杂的磁各向异性最大,远高于其他5d原子的掺杂,达到11.622meV;Au,W,Os和Hg掺杂的磁各向异性分别为3.847,2.219,1.376和0.098 meV; z轴方向的能量大于x轴方向的能量,x轴方向的能量更低,说明自旋平行于A lN平面时更稳定.第二类是磁各向异性为负值,Hf和Pt掺杂的磁各向异性分别为−0.014和−0.047 meV,z轴方向的能量小于x轴方向的能量,z轴方向的能量更低,说明自旋垂直于A lN平面时更稳定.

4 结 论

采用基于密度泛函理论的第一性原理计算方法,系统地对5d过渡金属元素掺杂2×2,3×3, 4×4和5×5六方氮化铝单层的几何结构、电子结构、磁性性质、铁磁态与反铁磁态能量差以及自旋耦合轨道效应导致的磁各向异性等进行了研究.研究发现,对于2×2,3×3,4×4,5×5这四种模型结构,Ta,Ir掺杂总态密度均呈现对称性,表明体系无磁性;而H f,W,Re,Os掺杂对于所有的模型结构总态密度均不对称,有磁性;Pt,Au,Hg这三种金属原子的掺杂,只有在2×2超胞中,总态密度呈现对称性,在3×3,4×4,5×5超胞中不对称.对铁磁态-反铁磁态的计算中,H f,Re,Pt和Au掺杂在4×8超胞中能量差达到最大值;Hg掺杂在3×6超胞,W和Os掺杂在2×4超胞中达到最大;其中, Re掺杂在4×8超胞中达到所有5d原子掺杂的最大值286.2320 meV.这说明在适当的掺杂浓度下,磁性中心之间会存在较强的交换相互作用.在对4×4超胞磁各向异性计算中发现,Re掺杂的磁各向异性能最大,达到11.622 meV,其他也较高,显示出较强的磁各向异性.结合以上结果,我们预测在适当掺杂浓度、并选择合适的5d原子,则六方氮化铝单层可能会存在二维长程磁有序.

[1]Novoselov K S,Geim A K,M orozov S V,Jiang D,K atsnelson M I,G rigorieva I V,Dubonos S V,Firsov A A 2005 Nature 438 197

[2]Cahangirov S,Topsakal M,Ak türk E,Sahin H,Ciraci S 2009 Phys.Rev.Lett.102 236804

[3]W ang Q H,Kalantar-Zadeh K,K is A,Colem an J N, Strano M S 2012 Nat.Nanotechnol.7 699

[4]Fleischer JW,Segev M,Efrem idis N K,Dem etrios N 2003 Nature 422 147

[5]Lu W,Lieber C M 2007 Nat.M ater.6 841

[6]Zhirnov V V,Cavin R K 2008 Nat.Nanotechnol.3 77

[7]Xu X D,Yao W,X iao D,Heinz T F 2014 Nat.Phys.10 343

[8]Aw schalom D D,F lattéM E 2007 Nat.Phys.3 153

[9]Prinz G A 1998 Science 282 1660

[10]Huang B,X iang H J,Yu J,W ei S H 2012 Phys.Rev. Lett.108 206802

[11]Cocchi C,Prezzi D,Calzolari A,M olinari E 2010 J. Chem.Phys.133 124703

[12]Chan K T,Lee H,Cohen M L 2011 Phys.Rev.B 83 035405

[13]M erm in N D,W agner H 1966 Phys.Rev.Lett.17 1133

[14]Luo H M,W ang D H,He J B,Lu Y F 2005 J.Phys. Chem.B 109 1919

[15]Xu C,Gao J,Gao C Y 2006 Acta Phys.Sin.55 4221 (in Chinese)[徐灿,曹娟,高晨阳2006物理学报55 4221]

[16]Kap lan B,Kap lan R 2014 J.M agn.M agn.M ater.356 95

[17]Ou X,W u H 2014 Sci.Rep.4 4609

[18]Liu C C,FengW X,Yao Y G 2011 Phys.Rev.Lett.107 076802

[19]Laguna-M arco M A,Haskel D,Souza-Neto N,Lang J C, K rishnam u rthy V V,Chikara S,Cao G,van Veenendaal M 2010 Phys.Rev.Lett.105 216407

[20]Zhang Z F,Zhou T G,Zhao H Y,W ei X L 2014 Chin. Phys.B 23 016801

[21]Shitade A,Katsura H,KunešJ,Qi X L,Zhang S C, Nagaosa N 2009 Phys.Rev.Lett.102 256403

[22]K ane C L,M ele E J 2005 Phys.Rev.Lett.95 226801

[23]He W Y,He L 2013 Phys.Rev.B 88 085411

[24]Zhang H B,Lazo C,B lügel S,Heinze S,M okrousov Y 2012 Phys.Rev.Lett.108 056802

[25]Hu J,A licea J,W u R Q,Franz M 2012 Phys.Rev.Lett. 109 266801

[26]X iao Z L,Shi L B 2011 Acta Phys.Sin.60 027502(in Chinese)[肖振林,史力斌2011物理学报60 027502]

[27]Sebastian K C,Chaw da M,Jonny L,Bodas D 2010 M ater.Lett.64 2269

[28]Chen S,Wu Q Y,Chen Z G,Xu G G,Huang Z G 2009 Acta Phys.Sin.58 2011(in Chinese)[陈珊,吴青云,陈志高,许桂贵,黄志高2009物理学报58 2011]

[29]Gonze X,Beuken JM,Caracas R,Detraux F,Fuchs M, Rignanese G M,Sindic L,Verstraete M,Zerah G,Jollet F,Torrent M,Roy A,M ikam i M,Ghosez P,Raty J Y, A llan D C 2002 Com put.M ater.Sci.25 478

[30]Gonze X,Am adon B,Anglade P M,Beuken J M,Bottin F,Bou langer P,B runeval F,Caliste D,Caracas R, CôtéM,Deu tsch T,Genovese L,Ghosez P,G iantom assi M,Goedecker S,Ham ann D R,Herm et P,Jollet F,Jom ard G,Leroux S,M ancini M,M azevet S,O liveira M J T,Onida G,Pouillon Y,Rangel T,Rignanese G M, Sangalli D,Shaltaf R,Torrent M,Verstraete M J,Zerah G,Zwanziger JW 2009 Com put.M ater.Comm un.180 2582

[31]Torrent M,Jollet F,Bottin F,Zérah G,Gonze X 2008 Com pu t.M ater.Sci.42 337

[32]Perdew J P,Yue W 1986 Phys.Rev.B 33 8800

PACS:31.15.es,68.65.–k,73.20.HbDOI:10.7498/aps.66.063102

E lectron ic structu res,m agnetic p roperties and sp in-orb ital coup ling eff ects of alum inum n itride m onolayers doped by 5d transition m etal atom s: possib le tw o-d im ensional long-range m agnetic orders∗

Yang M ing-Yu Yang Qian Zhang Bo†Zhang Xu Cai Song Xue Yu-Long Zhou Tie-Ge

(College of E lectronic Inform ation and Op tical Engineering,Nankai University,T ianjin 300350,China)
(Received 27 Novem ber 2016;revised m anuscrip t received 28 Decem ber 2016)

Them agnetism of two-dim ensionalm aterial is an im portant research topic.In particular,the long-rangem agnetic order of two-dim ensional m aterial is of great significance in theoretical research and practical app lication.According to the Merm in-Wagner theory,the isotropic Heisenberg model in a two-dimensional system cannot p roduce long-range m agnetic orders at non-vanishing tem peratures.Considering the existence of strong m agnetic anisotropy,possible twodim ensional long-rangem agnetic ordersm ay exist in 5d atom doped two-dim ensionalalum inum nitride(A lN)m onolayer. This research is performed by fi rst-princip les calculations based on the density functional theory.Geometries,electronic structures,m agnetic p roperties,and m agnetic anisotropy energies from spin-orbital coup ling eff ects in A lN m onolayers doped by 5d transition m etal atom s(H f,Ta,W,Re,Os,Ir,Pt,Au,and Hg)are calculated.Four kinds of supercells are used in the calcu lation,i.e,2×2,3×3,4×4,and 5×5,w ith one alum inum atom substituted by one 5d atom.Projection augm ented wavem ethod is used to describe the interaction between the valence electrons and the ions.The p lane wave is used to expand the wave function of the valence electron.For an optim ized geometry,the bond length between the 5d m etal atom and the nearest N atom is the largest in Hg-doped supercells,which is 2.093Å,followed by the Au,H f, Pt,Ta,and Ir according to the order of bond length m agnitude.For the densities of states(DOSs),obvious im purity energy levels appear in the forbidden bands.For all the supercells,spin-up and spin-down DOSs of Ta and Ir doped system s are symm etric,indicating non-m agnetic states.DOSs of H f,W,Re,and Os doped system s are asymm etric, indicating m agnetic states.For Pt,Au,and Hg,DOSs are symm etric in 2×2 supercells,but asymm etric in the 3×3, 4× 4,and 5×5 supercells.Totalmagnetic moments and the spin densities are also given.In 5×5 supercells,they are 1.00,0.00,0.39,1.99,1.17,0.00,1.00,2.00,and 1.00 for H f,Ta,W,Re,Os,Ir,Pt,Au,and Hg,respectively.The m agnetic m om ent ism ain ly concentrated in the vicinity of the 5d atom s.The energy diff erences between ferrom agnetic and antiferromagnetic states are calcu lated.For H f,Re,Pt and Au system s,the diff erences in 4×8 supercells reach the m aximum values of−187.2563 m eV,286.2320 m eV,−48.0637 m eV and−61.7889 m eV,respectively.The results indicate that there is a strong interaction between them agnetic centers.M agnetic anisotropy energy originating from spin-orbital eff ect is calcu lated in the 4×4 supercells.For the Re system,it is the highest,reaching 11.622 meV.For W,Os,and Au,the values are larger than 1 m eV,show ing strong m agnetic anisotropies.Them agnetic anisotropy can produce a spin wave energy gap,resulting in long-rangemagnetic orders.Based on the results above,it is p redicted that w ith appropriate 5d atom s and suitable doping concentration,two-dim ensional long-rangemagnetic ordersm ay exist in 5d transition m etal atom doped A lN m onolayers.

alum inum nitridemonolayer,fi rst-principles,density functional theory,spin-orbital coupling

10.7498/aps.66.063102

∗天津市自然科学基金(批准号:13JCQNJC00500)资助的课题.

†通信作者.E-m ail:zhangbo2010@nankai.edu.cn

*Pro ject supported by the Natural Science Foundation of T ian jin,China(G rant No.13JCQNJC00500).

†Corresponding author.E-m ail:zhangbo2010@nankai.edu.cn