纤维弹性细杆模型动力学分析的有限元方法及应用

刘忠乐, 华志宏, 薛文良

(东华大学 a．理学院；b．纺织面料技术教育部重点实验室, 上海 201620)

纤维弹性细杆模型动力学分析的有限元方法及应用

刘忠乐a, 华志宏a, 薛文良b

(东华大学 a．理学院；b．纺织面料技术教育部重点实验室, 上海 201620)

基于纺织工程中的气流辅助加捻纺纱, 以弹性细杆作为纤维模型, 讨论纤维空间大变形的动力学问题．采用空间杆单元有限元分析方法, 对弹性细杆动力学分析的有限元模型进行简化, 导出了弹性杆单元刚度方程和刚体质量单元动力学方程, 然后综合出弹性细杆整体的动力学运动微分方程．节点坐标姿态采用欧拉四元素表示, 导出了相关的坐标变换矩阵．以此方法对气流辅助加捻纺纱动力学模型进行实例计算．

纤维模型；弹性细杆；有限元；动力学分析

随着气流技术在纺纱加工过程中的广泛应用, 在其工艺机理研究中迫切需要通过数值模拟来了解纤维在各种复杂受力状态下的运动行为．纤维是一种具有一定弹性的且超大长径比的柔性连续体材料, 近年来一般都将纤维简化成珠链模型[1-2]进行分析计算．由于珠链模型不考虑纤维各截面的角位移, 故不能准确表达纤维的弯曲与扭转特性．本文同时考虑纤维各截面的线位移和角位移, 把纤维看作连续的弹性细杆进行研究．虽然目前关于弹性细杆几何大变形动力学问题的研究已经有了较完整的理论[3], 但现有的理论和方法都是以多参数表达的联立偏微分方程组来表述弹性细杆的力学行为, 较难用于一般空间三维问题的实际数值计算, 其实际应用的相关研究极少．本文采用有限元方法计算弹性细杆三维空间几何大变形动力学问题, 导出了弹性杆单元刚度方程和刚体质量单元动力学方程, 然后综合出弹性细杆整体的动力学运动微分方程, 并以此方法进行数值模拟并计算了某气流辅助加捻纺纱工艺中纤维在气流驱动下随时间的运动演变过程．

1 弹性细杆动力学分析的有限元模型 简化

采用有限元方法对弹性细杆进行动力学分析．将整个弹性细杆分割成n+1个相互独立的微段, 在每个微段中点的横截面中心设置一节点, 每个节点横截面固结一连体动坐标系, 即节点坐标系．将固定于地面的惯性参考系作为有限元分析的总体坐标系．每个节点坐标系相对于固定总体坐标系有6个自由度, 设置6个坐标参数确定其相对位置, 其中3个描述节点的移动线位移, 其余3个描述节点横截面转动角位移．考虑弹性细杆的质量时, 将每个微段的质量看作随其节点坐标系作空间一般运动的刚体(见图1)．考虑弹性细杆的弹性时, 将每相邻两节点之间看作为只计弹性不计质量的空间弹性杆单元的相连接(见图2)．作用于弹性细杆上的外力都向其节点简化．

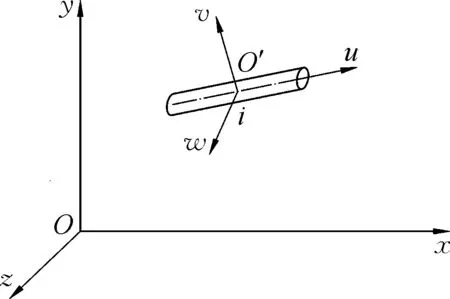
图1 作空间一般运动的微段刚体Fig.1 Rigid body unit for general motion in space

图2 弹性细杆的弹性杆单元有限元模型Fig.2 Finite element model of elastic bar elements of elastic thin rod

2 微段刚体空间一般运动的动力学方程

弹性细杆动力学分析有限元模型中随某节点i作空间一般运动的微段刚体如图1所示．图中Oxyz为固定总体坐标系,O′uvw为固结于刚体的连体动坐标系, 即节点坐标系, 其坐标原点位于刚体质心, 坐标轴方向为该刚体质心惯性主轴方向,u轴为微段刚体的轴线方向,v和w轴位于微段刚体过质心的横截面上．

刚体在空间的任意一般运动可分解为随其质心的平移和相对于质心的转动．根据质心运动定理知, 刚体随质心O′平移的动力学方程为

ma=F

(1)

式中:m为刚体质量；a为质心相对于固定总体坐标系Oxyz的绝对加速度；F为刚体上外力的主矢．

根据动量矩定理[4], 可导出刚体绕质心O′转动的动力学方程为

Jα+ω×(J·ω)=M

(2)

式中:J为刚体对质心的惯量；M为刚体上外力对质心的主矩;ω为刚体的角速度；α为ω相对动坐标系O′uvw对时间的导数.可以证明α也等于ω相对定坐标系Oxyz对时间的导数.

合并式(1)和(2), 可将节点i微段刚体的动力学方程写成矩阵形式为

(3)

或简写为

(4)

相对于定坐标系Oxyz, 式中

(5)

(6)

(7)

其质量矩阵为

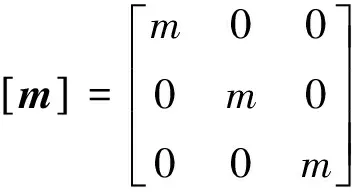
(8)

设微段刚体相对质心惯性主轴O′uvw的惯量为

(9)

则

(10)

式中O′uvw相对于Oxyz的方向余弦矩阵为

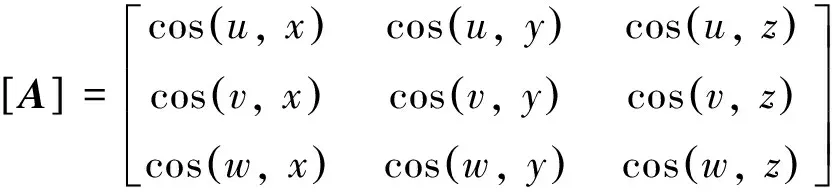
(11)

3 以节点坐标位置表示弹性杆单元的 杆端力

图2中的任意某相邻的两个节点及其之间的弹性杆单元如图3所示, 其中i和j为弹性细杆在任意时间t的节点位置．取节点i的节点坐标系作为该单元的局部坐标系, 坐标面O′vw位于节点i的横截面上,i-j0位置为杆单元无受力变形的参考位置．

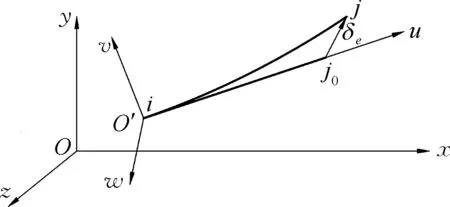
图3 弹性杆单元和局部坐标系Fig.3 Elastic bar element and local coordinate system

弹性杆单元的杆端变形位移与杆端力相对于总体坐标系Oxyz的关系可表示为

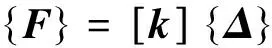
(12)

式中单元相对Oxyz的杆端力和杆端变形位移为

而单元刚度矩阵

(13)

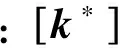
现因取节点i的节点坐标系O′uvw作为该单元的局部坐标系(见图3), 故有

(14)

而

(15)

记

则由式(12)可将杆单元e的刚度方程写成

(16)

由此即可根据各节点坐标位置得出各弹性杆单元的杆端力．

4 弹性细杆有限元总体动力学分析

对于固结于每个节点i的微段刚体, 式(4)为对应于每个节点的6个自由度表示的动力学方程．现将其节点自由度编号转换为总体节点自由度编号, 将式(4)改写成

(17)

对于每个弹性杆单元e, 将式(16)表示的每个弹性杆单元的节点力按对应于总体节点自由度编号进行转换,将其改写成

(18)

(19)

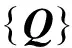
将式(17)和(18)代入式(19), 得

(20)

式中：

(21)

(22)

(23)

式(20)即为弹性细杆有限元总体动力学分析的运动微分方程．

5 节点坐标系姿态的欧拉四元素坐标 表示

根据刚体有限转动的欧拉定理, 图1中任意节点坐标系O′uvw相对于总体坐标系Oxyz的姿态方位, 可看作是过O′点的xyz方位绕过O′的某单位矢量p转动某θ角而实现．设单位矢量p在Oxyz坐标系的坐标为(p1,p2,p3), 可定义以下4个变量[7]

(24)

作为欧拉四元素坐标, 用于表示节点坐标系的姿态方位.

直接验算可证实欧拉四元素之间存在如下关系

(25)

因此, 欧拉四元素中只有3个独立变量.

可以导出以欧拉四元素表示的节点坐标系O′uvw相对于总体坐标系Oxyz的角速度为

(26)

图3和式(15)中节点j的方位相对i的微小角位移为

(27)

式(11)所示的方向余弦矩阵为

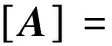
(28)

由此对有限元总体动力学分析的运动微分方程式(20)进行数值积分, 就可求得整个弹性细杆各节点在不同时刻的速度和位置．

6 实 例

纺织工程中的一种气流辅助加捻过程简化模型如图4所示．图4中大圆柱为固定的空心腔体, 内部中心圆柱体CD代表中心须条, 被看作相对固定的刚体, 偏心小圆柱AB为一根做包缠运动的纤维, 被看作弹性细杆, 其A端固定,B端自由, 假设在图示初始位置的速度为零．在腔体内存在有做高速螺旋运动的旋转气流, 其气体绕中心x轴高速旋转, 同时沿着x轴方向低速移动．现分析包缠纤维在高速气流的驱动下逐渐缠绕到中心须条上的动力学过程．

图4 气流辅助加捻纺纱的动力学模型Fig.4 Dynamic model of airflow assisted twisting yarn

采用本文的有限元方法进行动力学分析, 将整个包缠纤维均分成n+1个微段, 对于气流作用于包缠纤维的分布荷载向节点简化．包缠纤维与刚性中心圆柱及腔体之间的接触约束采用罚函数法处理, 即在两者之间恰当地构造一个排斥力, 该力在两者之间的距离较接近时快速增大, 而存在一定距离后就快速衰减到零．运用Matlab编程计算, 代入具体数据, 求得包缠纤维在一系列不同时刻的包缠形态位置如图5所示．

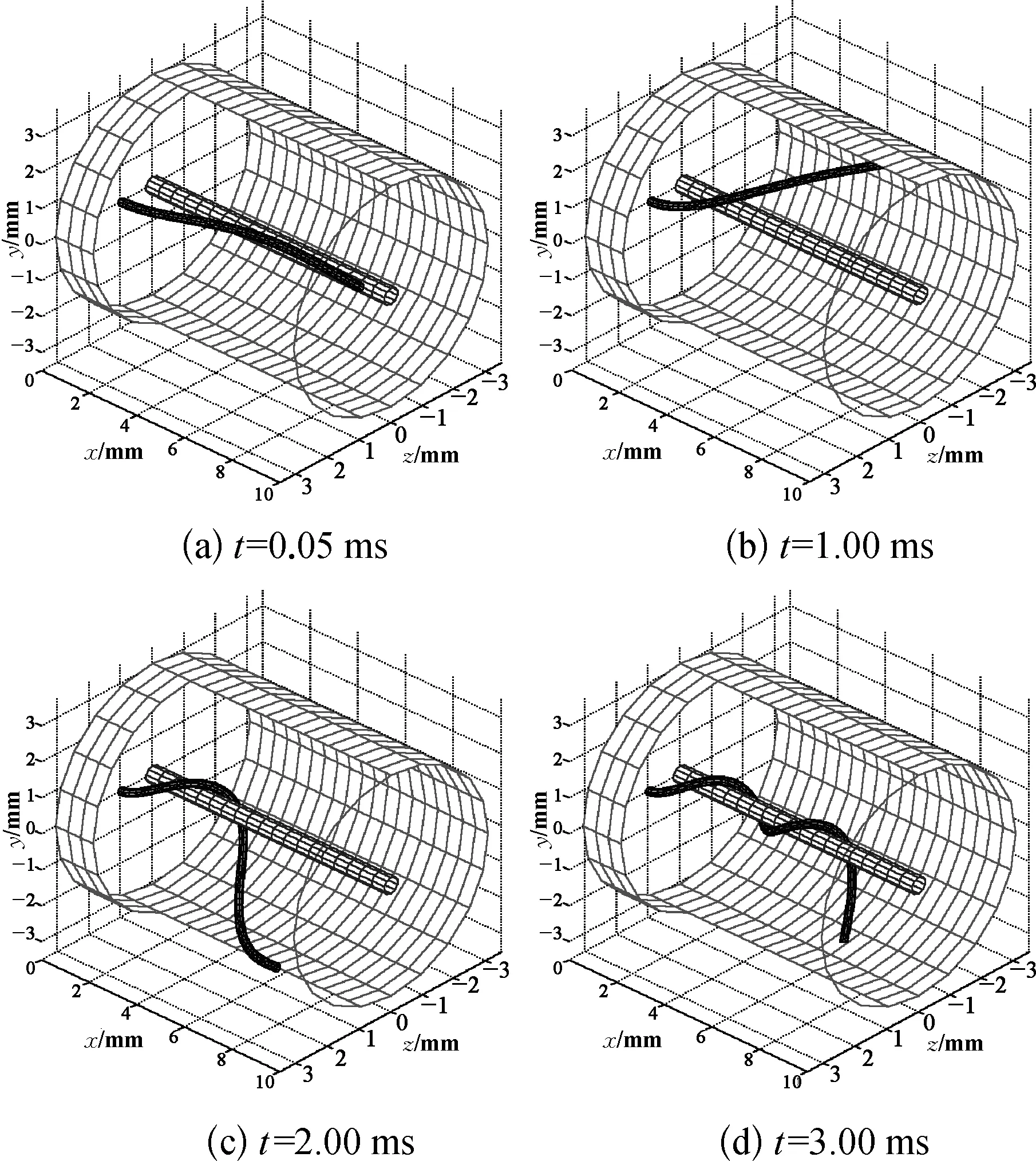
图5 包缠纤维随时间变化的包缠过程Fig.5 The wrapping process of wrapping fiber with time

7 结 语

为研究纤维空间运动动力学过程, 本文以弹性细杆作为纤维模型, 采用有限元方法建立了弹性细杆总体动力学分析的运动微分方程, 并以此方法模拟了一种气流辅助加捻过程中纤维在气流驱动下随时间的动力学运动演变过程, 可为其纺纱设备与工艺的设计与改进提供理论基础．本文为纺织工程中数值模拟纤维在各种不同气流驱动下的动力学运动过程的建模提供了理论方法．

[1] YAMAMOTO S, MATSUOKA T. A method for dynamic simulation of rigid and flexible fiber in a flow field [J]. Journal of Chemical Physics, 1993, 98(1): 644-650.

[2] 张勇, 曾泳春, 王云侠, 等．基于珠-杆模型的喷气涡流纺喷嘴气流场中的纤维运动规律[J]．东华大学学报(自然科学版), 2013, 39(5): 583-589．

[3] 刘延柱．弹性细杆的非线性力学[M]．北京: 清华大学出版社, 2006: 124-150．

[4] 刘延柱．高等动力学[M]．北京: 高等教育出版社, 2001: 105- 118．

[5] 赵经文, 王宏钰．结构有限元分析[M]．北京: 科学出版社, 2001: 17-20．

[6] 李二明, 华志宏, 薛文良, 等．纤维弹性细杆模型几何大变形静力学分析的有限元方法[J]．东华大学学报(自然科学版), 2016, 42(6)：916-921．

[7] 洪嘉振．计算多体系统动力学[M]．北京: 高等教育出版社, 1999: 44-46．

(责任编辑: 杨 静)

Finite-Element Method and Application of Dynamic Analysis of Fiber Elastic Thin Rod Model

LIUZhonglea,HUAZhihonga,XUEWenliangb

(a．College of Science；b．Key Laboratory of Textile Science & Technology,Ministry of Education, Donghua University, Shanghai 201620, China)

Based on the airflow assisted twisting of yarn spinning in textile engineering, the dynamic problems of this model’s spatial large deformation were discussed using the elastic thin rod as the fiber model. Using spatial bar finite-element method for the dynamic analysis of elastic thin rod model, the spatial bar element stiffness equation and the rigid body mass unit dynamic equation were derived, and then the kinetic differential equations of whole elastic thin rod were synthesized. Also, the related coordinate transformation matrices were obtained using the Euler quaternion for the determination of node coordinate attitude. As an example, the method was used in calculation of the airflow assisted twisting spinning dynamics model.

fiber model; elastic thin rod; finite-element; dynamic analysis

1671-0444 (2017)03-0454-05

2016-06-13

刘忠乐(1993—)，男，湖北石首人，硕士研究生，研究方向为固体力学．E-mail: 2141386@mail.dhu.edu.cn 华志宏(联系人)，男，副教授，E-mail: hzh@dhu.edu.cn

TS 101.2

A