度相关性对无向网络可控性的影响∗

徐明 许传云 曹克非

1)(云南大学物理与天文学院,非线性复杂系统中心,昆明 650091)

2)(凯里学院数学科学学院,凯里 556011)

3)(贵州财经大学数学与统计学院,贵阳 550025)

度相关性对无向网络可控性的影响∗

徐明1)2)3)许传云1)曹克非1)†

1)(云南大学物理与天文学院,非线性复杂系统中心,昆明 650091)

2)(凯里学院数学科学学院,凯里 556011)

3)(贵州财经大学数学与统计学院,贵阳 550025)

(2016年7月23日收到;2016年9月5日收到修改稿)

复杂网络的可控性不仅与网络的度分布有关,还受到度相关性的影响,但这种影响在无向网络的情况下尚不清楚.本文采用模拟退火算法,通过边的重连改变网络的度相关性从而研究其对网络可控性的影响.数值模拟结果显示,在度分布不变的情况下,无向网络的可控性指标(驱动节点密度)一般随着度相关系数的增大而单调减小;进一步研究表明,双向网络和某些有向网络也遵循这种规律.无向网络的度相关系数增大意味着对应有向网络的各种度相关系数同步增大,但这些综合变化对网络可控性的影响不能简单归结为对应有向网络中各影响的叠加.本文对这种现象给出了部分解释.此外,对于无自环的大型稀疏网络,无论其同配还是异配,验证了其结构可控性与严格可控性是几乎相同的.这些研究将深化对网络可控性与网络结构之间关系的理解.

复杂网络,无向网络,可控性,度相关性

1 引 言

对复杂网络进行控制是分析和研究复杂网络系统的一个重要目标,也是当前复杂网络研究的热点[1-12].其中,各种复杂网络乃至各种复杂系统是否可控(即可控性问题)是极为关键且有着广泛科学意义和应用价值的研究课题[1,4,9],例如,选择哪些基因作为药物的靶标来调控整个基因网络,从而实现对一些疾病的治疗等.系统的可控性也叫能控性,如果系统所有的状态变量都可以通过输入来影响和控制而在有限时间内由任何初始状态达到所期望的目标状态,则称系统是可控的,或者更确切地说是状态可控的,否则就称系统是不可控的[1,13].可控性的基础理论在数学上已较为成熟,并被广泛应用于工程中.然而,实践中要把传统的可控性理论直接应用到复杂系统或网络却往往是困难的[4,9,14].如何控制一个节点众多的复杂系统呢？首要问题是至少需要多少外界输入信号才能使系统可控,也就是满足可控性条件的控制器的最少个数问题.由于计算复杂度太大,该问题很难直接通过传统的Kalman秩条件[13]来解决.2011年,Liu等[1]在《自然》上发表了关于复杂网络的结构可控性(structural controllability)论文,开拓性地将传统的结构可控性理论[15]应用到网络的结构可控性问题,对网络结构可控所需的最少输入和最小驱动节点集做了深入研究：通过引入图的匹配[16]得到了求解最少输入信号和驱动节点的最少(最小)输入定理;通过cavity方法[17]揭示了驱动节点密度nD(可控性指标)与网络结构的深层联系.这一突破性工作引发了复杂网络可控性研究的热潮.由于结构可控性忽略了网络中边权的大小和相互联系,因此该理论对某些网络(如无向网络)不适用.2013年,Yuan等[3]从Popov-Belevitch-Hautus(PBH)可控性判据[18]出发提出了求解网络严格可控性(exact controllability)的理论框架,可用于求解具有确定性边权和任意结构的网络的可控性(如无向无权网络的可控性),使得网络可控性的理论更加完备.这里需要说明的是,牵制控制[19]是复杂网络系统控制研究的另一个重要方向,其目的是通过有选择地对网络中的少数节点施加控制而使整个网络系统达到所期望的行为(使网络中每个节点的轨迹“收敛”到某条期望的轨迹);结构可控性则主要研究系统是否可控,即系统状态变量能否在有限时间内“到达”任何期望的状态.由于研究目的不同,牵制控制与结构控制在驱动节点的选择上差异较大[1,20-22],本文将不研究牵制控制.

文献[1]给出一个重要结论：复杂网络的结构可控性主要取决于网络的度分布.随后的研究发现,复杂网络的可控性不能由网络的度分布惟一确定,它还与度相关性有联系[2,9,10].在保持网络度分布不变的情况下,文献[2]分别从入度-入度相关性、入度-出度相关性、出度-入度相关性和出度-出度相关性四个方面系统地研究了一般有向网络的度相关性对网络的结构可控性的影响.其中,四种度相关性对有向Erdős-Rényi(ER)随机网络的结构可控性的影响规律如图1所示,对有向无标度(scale-free)网络也有类似的结果.

图1 度相关系数对有向ER随机网络(节点数N=10000)的结构可控性指标nD的影响 网络的平均度分别为〈k〉=1(红色),〈k〉=3(绿色),〈k〉=5(蓝色),〈k〉=7(黑色)和〈k〉=9(橙色);每一数据点为100次独立模拟的平均;对有向无标度网络也有类似的结果(引自文献[2])Fig.1.The impact of degree correlation coefficients on the structural controllability measurenDfor the directed ER random network(N=10000)for average degrees〈k〉=1(red),〈k〉=3(green),〈k〉=5(blue),〈k〉=7(black)and〈k〉=9(orange).Each data point is an average of 100 independent runs.The results are similar for the directed scale-free network(cited from Ref.[2]).

然而,两种或两种以上的度相关性的共同变化会如何影响网络的可控性则没有彻底解决,这类问题也显得更加复杂.例如,当四种度相关系数同步变大并趋近于1时,可控性将如何变化？另外,是否所有的有向网络均遵循文献[2]所得规律也值得探究.在网络拓扑变化时,往往是多种度相关性同时发生变化,或者说一种度相关性变化的同时也常伴随着其他类型度相关性的变化.一个常见的例子就是对无向网络进行边的重连变换.无向网络可以看成特殊的有向网络,无向网络中两节点相连意味着它们彼此指向对方.本文就以无向网络及其推广形式为研究对象来探索度相关性对网络可控性的影响,分析其与一般有向网络情况下相关结论的异同.

本文后续内容安排如下：首先介绍网络可控性和度相关性的概念;接着对无向网络及对应有向网络中的度相关性对网络可控性的影响进行数值模拟和分析;最后对模拟结果进行讨论.

2 相关理论

2.1 网络的结构可控性

考虑一个线性时不变系统,其动力学方程描述为[1,3]

将状态变量看作节点,结合它们的相互作用可形成对应的网络.其中向量x(t)=(x1(t),x2(t),···,xN(t))T和u(t)=(u1(t),u2(t),···,uM(t))T分别表示t时刻网络中N个节点的状态和M个输入控制信号的状态;A∈RN×N是节点间的耦合矩阵,B∈RN×M是输入控制信号与节点的连接关系矩阵.

通过传统的Kalman秩条件[13]来得到网络可控所需的最少输入或驱动节点,其计算时间复杂度为O(2N),这对于大规模的复杂系统或复杂网络而言很难实现.但人们发现,如果存在矩阵A和B中的非零元素的一组取值,使得在这组值下的系统是可控的,则网络中的待定边权参数几乎可以任意变化(保持非零)而不会破坏系统的可控性,这时的网络被称为是结构可控的[15].结构可控性的引入有效地解决了现实世界中无法准确度量边权的问题,极大地推动了可控性的应用研究.Lin[15]提出的结构可控性定理从图论的角度分析了结构可控性.在此基础上,Liu等[1]将一般有向网络的结构可控性问题转化成求解有向图的最大匹配,给出了如下的最少输入定理.

定理1如果网络是完全匹配,则使网络结构可控所需的最少输入数目或最少驱动节点数ND是1,此时任选一个节点都可作为网络的驱动节点;如果网络不是完全匹配,则最少驱动节点数ND等于网络最大匹配后未匹配节点的数目：

其中|M∗|为有向网络中最大匹配M∗所对应的匹配节点数,此时需独立控制的驱动节点恰是未匹配节点.

需要注意的是,网络的最大匹配的具体形式可能不惟一,因而驱动节点的选择可能不惟一,但最少驱动节点数ND是不变的.

2.2 网络的严格可控性

结构可控性主要针对网络中每条(有向)非空连接的权重不确定且边权间相互无关联的情况[1,15].当边权有关联或边权精确可知时,使用结构可控性理论所得结果可能会不够准确,此时应采用网络的严格可控性理论.严格可控性理论从PBH秩条件出发,证明了网络系统(1)满足可控性条件所需的最少输入数目或最少驱动节点数ND应为[3]

其中µ(λi)是耦合矩阵A的特征值λi的几何重数.网络的严格可控性理论认为,无自环或少自环的大型稀疏网络中零特征值的几何重数最大,又由于此时零特征值的几何重数可计算为µ(0)=N-rank(A),故可得如下最少驱动节点数ND的快速计算方法.

定理2对于大型稀疏网络(有向或无向,加权或无权,无自环或少量自环),网络系统(1)满足可控性所需的最少输入数目或最少驱动节点数ND为[3]

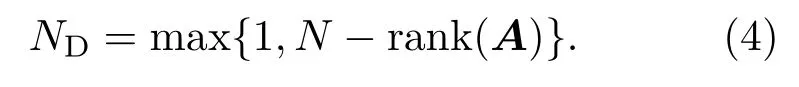
一般地,网络的可控性度量指标(controllability measure)定义为使网络可控所需的最少驱动节点在网络节点中所占的比例,即网络中的驱动节点密度(density of driver nodes),记为

该指标从控制输入的需求比例上反映网络的可控难易程度,nD越小的网络越容易控制,反之则网络越难于控制.

如果一个网络的边权是固定且精确可知的,则可采用网络的严格可控性理论求解其可控性.但通常情况下,人们知道某些节点间存在连边,却无法获取或难以精确测量边权的值,另外边权还可能随时间而变化(保持非零),此时可以转而利用网络的结构可控性理论求解其可控性.虽然一个网络系统是结构可控的并不等同于该系统一定可控,但可以说该系统几乎(以概率为1的可能发生)是可控的.

2.3 网络的度相关性

通常,人们用网络的度分布描述网络的拓扑结构特征.然而,这种描述有一个重要缺陷,即很难反映节点连接时的度的混合程度.度相关性则在本质上反映了不同度值节点间的连接倾向(偏好性)：如果度值高(低)的节点倾向于与其他度值高(低)的节点连接,那么该网络关于度是同配的;反之,则称该网络是异配的[23].大量研究表明,真实网络中的很多社会网络关于度是同配的,而很多技术网络和生物网络关于度是异配的.度相关性对网络传播现象、博弈演化、随机游走和网络可控性有着不可忽视的影响.如果不考虑度相关性,通常将导致研究结果的片面性或不准确性.实践中,可以通过Newman提出的计算网络度相关性的Pearson系数来进行量化,该系数具体定义为[23]

其中,ji和ki分别为第i条边的两个端点的度(与其直接相连的边数),M为网络中的边数.度相关系数(6)式对于无向和有向网络均适用.特别地,对于有向网络,利用以上Pearson系数可得到四种度相关系数：入度-入度相关系数、入度-出度相关系数、出度-入度相关系数和出度-出度相关系数,具体计算公式可表为[2,24]

其中,E是有向边的数目,表示关于每一条边求和;α,β∈{in,out}为入度或出度;和分别是关于有向边e的起始节点的(α)度和末端节点的(β)度;是起始节点的平均度,是对应的标准偏差;kβ和σβ类似.以上两个相关系数(6)式和(7)式实质上是一致的.无向网络可以看作有向网络的特殊情况,此时无向网络的度相关系数((6)式)与对应有向网络的四种度相关系数((7)式)均相等.

3 主要方法

这里主要对无向网络及其推广形式进行讨论.无向网络可以看作特殊的有向网络：将一条无向边看作一对有向边,无向网络G就直接推广为对应的双向网络.当双向网络的边权均确定时,例如边权均为1,我们可求解其严格可控性;当双向网络的边权非零但无法准确测量时,则求解其结构可控性.现有结果表明,在不考虑度相关性的因素时,无自环的大型稀疏网络的结构可控性(利用(2)式)与严格可控性(利用(4)式)保持较高程度的一致[3].在度相关性发生较大变化时,此结论是否成立尚不清楚.

为了研究度相关性对网络可控性所产生的影响,通常对网络做边的重连变换[2,25,26],它可以在保证网络度分布不变的情况下改变度相关性.这里用图例来说明边的重连变换.假设在初始无向网络G中随机挑选到一对边为AB和CD,如果A与D之间、C与B之间均无连边,则对无向网络G和对应双向网络可进行边的重连变换,具体如图2所示.

从(6)式和(7)式不难看出,这里的度相关系数由网络的拓扑结构决定,即只与节点的连接方式有关,而与边的权重无关.如果重连后(图2(a))无向网络G的度相关性发生变化,则对应双向网络在双向边重连后(图2(b))各种度相关性也发生着完全同步的变化.图2(c)所示则是对双向网络进行一般性的有向边重连,所得网络虽为更一般的有向网络,但所得网络的四种度相关系数仍然彼此相等,即有向边重连过程导致的各种度相关性同步变化.正如图2(c)所示：有向边A→B和C→D重连为A→D和C→B,则出度-出度关系相应地从1→2和3→4转化成1→4和3→2,且出度-入度、入度-入度和入度-出度关系也同时经历着一样的变化.基于此,只需研究双向网络的某一种度相关系数(例如出度-出度相关系数)对可控性的影响即可,其余度相关系数对可控性的影响与之完全相同.

图2 边的重连示意图 (a)无向网络的无向边重连：随机挑选一对无向边AB和CD,如果A与D之间、C与B之间均无连边,则让A改为与D连接,C改为与B连接,从而将所挑选出的那一对边重连成一对新边AD和CB;(b)双向网络的双向边重连;(c)双向网络的一般性有向边重连Fig.2. Schematic diagramsoflink rewiring：(a)Rewiring of undirected edges in an undirected network：after a pair of undirected edgesABandCDis randomly selected,these edges are then rewired by connectingAtoD,whileCtoB,provided that none of these edges already exist in the network;(b)rewiring of bidirectional edges in a bidirectional network;(c)rewiring of directed edges in a bidirectional network.

为了方便叙述,当网络的边权不确定且相互无关联时,在双向(bidirectional)边重连变换下的结构可控性记为SCb,在一般有向(directed)边重连变换下的结构可控性记为SCd;当网络的边权确定为1时,在双向边(或无向边)重连变换下的严格可控性记为ECb,在一般有向边重连变换下的严格可控性记为ECd.文献[2]讨论的是在一般有向边重连变换下的结构可控性,即SCd.

对于边权不确定且边权之间相互无关联的双向网络,我们讨论其结构可控性,可用最大匹配的方法求其最小驱动节点集.注意双向网络的最大匹配不同于无向网络的最大匹配.如图3所示：在求解双向网络(图3(b))的最大匹配时,不能等同于无向网络(图3(a))的最大匹配,而要将网络转化为无向二分网络(图3(c))来求其最大匹配.对于无向二分网络,具体可采用Hopcroft-Karp算法[27]求解其最大匹配.

图3 无向网络和对应双向网络的最大匹配 (a)简单无向网络的最大匹配;(b)由(a)推广的双向网络及其最大匹配;(c)与(b)对应的二分网络及其最大匹配.其中,红色边为匹配连边,绿色点为匹配节点.无向网络(a)的最大匹配无法包含全部节点,而对应双向网络(b)的最大匹配为完全匹配,包含全部节点Fig.3.Maximum matchings in an undirected network and its corresponding bidirectional network：(a)Maximum matching of a simple undirected network;(b)maximum matching of the bidirectional network generalized from(a);(c)maximum matching of the bipartite network corresponding to(b).Among them,the red edges are matched edges,and the green nodes matched nodes.In the undirected network(a),the maximum matching cannot contain all nodes of the network;while in the corresponding bidirectional network(b),the maximum matching is a perfect matching which contains all nodes.

为了更有代表性地对各类网络进行讨论,理论模型选用ER随机网络模型(典型的同质网络)和无标度网络模型(常见的异质网络).然而,一般的BA无标度网络可能会导致不必要的度的相关性,并可能大大限制通过重新连边所能得到的度相关系数的范围.文献[28]对使用重连方法产生反匹配无标度网络的有效性进行的专门探讨表明,在BA无标度网络中,度相关性本质上受到度分布的制约,特别是在网络规模较大和节点度差异性较强时,重连所产生的异配效果较差.

为了克服这些困难,这里先引入一个生成无标度网络的统计模型[29].设网络系统的初始状态有N个节点,每个节点用一个整数i(i=1,2,...,N)进行标记.然后我们再对每个节点赋予一个权重pi=i-τ,其中τ是位于区间[0,1)内的控制参数.接下来,我们以归一化的权重值和为概率随机选取两个节点i和j,若选取的两个节点之间没有连边,则在它们之间添加一条边.持续该过程直到系统中有mN条连边,从而使网络平均度为2m.由于连边概率与节点的权重相关,因而节点i的度ki满足

以上模型只是从统计角度构造了无标度网络,并未从根本上改变无标度网络对度相关性的制约.下面做进一步改造[2]：对节点i赋予权重pi=(i+i0)-τ,其中i0为可调参数,取值约为网络平均度的2倍.改造后的无标度统计模型能生成近似的无标度网络,既保持网络的异质特性,又能适当扩大重连变换下网络度相关系数的变化范围.这种改造也是合理的,因为现实中的无标度网络大多是近似的.

为了通过边的重连变换有效地改变度相关系数,这里采用模拟退火算法[30]来具体实现.设定目标度相关系数r∗并定义能量函数E(r)=|r-r∗|,可按照下列步骤调节网络的度相关系数：

1)对初始网络计算出度相关系数r和对应的能量E(r),并初始化温度参数T和每个T值的迭代次数L;

2)任意选择两条合适的连边,对它们做边的重连变换,计算变化后的能量E(r′),并得到增量ΔE=E(r′)-E(r);

3)按Metropolis准则,以一定的概率接受此种换边方式：若ΔE≤0则直接接受该换边方式,否则以概率exp(-ΔE/(kBT))接受该换边方式(kB为Boltzmann常数).当新的连边方式被确定接受时,相应地更新能量函数的值,并在此基础上开始下一轮连边试验.而当新连边被判定为舍弃时,则在原网络状态的基础上继续下一轮试验.

4)如果|E(r)-E(r∗)|的数值小于给定的阈值(这里取为0.01)则停止计算.否则逐渐减小T值,并返回步骤2重复此过程.

4 模拟结果

图4 在无向边重连变换下,无向无权网络的度相关系数对网络严格可控性指标nD(ECb)的影响 (a)ER随机网络(节点数N=10000)的情况;(b)无标度网络(节点数N=10000)的情况.网络的平均度分别为〈k〉=1/2(红色),〈k〉=3/2(绿色),〈k〉=5/2(蓝色),〈k〉=7/2(黑色)和〈k〉=9/2(橙色).每一数据点为50次独立模拟的平均Fig.4.The impact of the degree correlation coefficient on the exact controllability measurenD(ECb)for undirected unweighted networks with rewiring of undirected edges for average degrees〈k〉=1/2(red),〈k〉=3/2(green),〈k〉=5/2(blue),〈k〉=7/2(black)and〈k〉=9/2(orange).Each data point is an average of 50 independent runs：(a)The results for the ER random network(N=10000);(b)the results for the scale-free network(N=10000).

我们先按照以上方法研究无向无权网络(边权为1)在无向边重连变换下度相关性对网络严格可控性(ECb)的影响.数值模拟结果如图4所示：在相同条件下,无标度(异质)网络比ER随机(同质)网络更难于控制;对于同样类型的网络,平均度越大则可控性指标(驱动节点密度)一般会越小,即稠密网络比稀疏网络更容易控制;无论是同质(均匀)网络还是异质(非均匀)网络,网络可控性指标nD(ECb)在整体上随着度相关系数r的增大而呈现减小的变化趋势;度相关性对可控性的影响有时非常显著,例如,对于平均度〈k〉=9/2的无标度网络,当度相关系数r=0时网络可控性指标约为0.13,而当度相关系数r=-0.6时网络可控性指标约为0.5.图4从平均值角度展示了度相关性对无向网络严格可控性(ECb)的影响.

接着,对双向网络进行边的重连变换,可类似地得到其他情形下度相关性与网络可控性的关系.例如,将无向网络看作边权不确定的双向网络,对该网络进行一般的有向边重连可以得到度相关性与有向网络结构可控性(SCd)的关系.有趣的是,双向网络的可控性SCb,ECb,SCd和ECd随度相关性的变化规律均与图4中ECb的变化规律表现出高度的一致性,其中无向网络与对应双向网络的ECb实质上是相同的.这里以平均度〈k〉=5/2的无向ER随机网络(仅考虑ECb)与对应双向网络为例,说明度相关性对各种可控性的影响高度地一致,具体如图5所示.从图5还可以看出,50次独立模拟得到的可控性指标的标准偏差不大,大都在0.02以内,即度相关系数对各种可控性指标(nD)的影响效应都是稳定的.

图5 对于ER随机模型(节点数N=10000),在边的重连变换下,无向无权网络(〈k〉=5/2)和对应双向网络(〈k〉=5)的度相关系数对各种可控性指标(nD)的影响.每一数据点为50次独立模拟的平均,误差线表示标准偏差Fig.5.The impact of the degree correlation coefficient on various controllability measures(nD)for the undirected unweighed network(〈k〉=5/2)and the corresponding bidirectional network(〈k〉=5)with rewiring of edges for the ER random model(N=10000).Each data point is an average of 50 independent runs,and the error bars denote the standard deviations.

实际上,网络的各种可控性指标除了变化趋势一致,相互间的数值差异也很小.为了进一步细致地考察图5中各种可控性之间的差异,选取以下两个指标对该差异进行探讨：

反映严格可控性指标与结构可控性指标在双向边(或无向边)重连下的相对偏差,其中表示双向边(或无向边)重连下边权均为1时的严格可控性指标nD(ECb)的平均值,表示边权不确定时的结构可控性指标nD(SCb)的平均值;

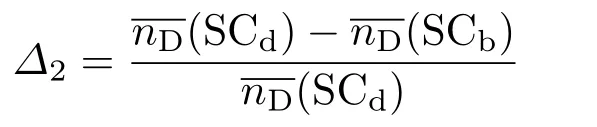
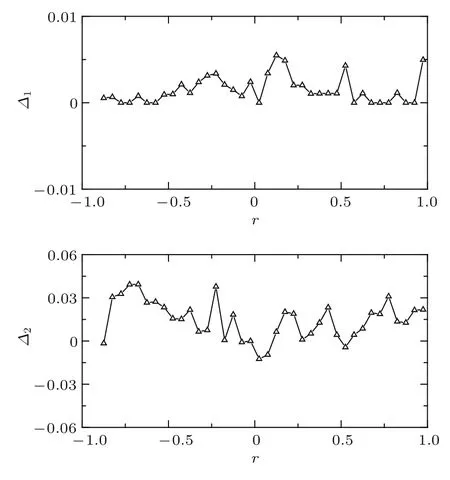
图6 无向ER随机网络与对应双向网络在边重连变换下几种可控性之间的相对偏差Δ1和Δ2 网络节点数N=10000,无向网络的平均度〈k〉=5/2Fig.6.Relative deviationsΔ1andΔ2of controllability measures for the undirected ER random network and its corresponding bidirectional network with rewiring of edges.The network size isN=10000,and the average degree of the undirected network is〈k〉=5/2.

下面比较一般有向网络与无向(或双向)网络情形下,度相关性对网络可控性的影响.从图1可知,一般有向网络在有向边的重连变换下,可控性指标与出度-入度相关系数呈现出稳定的单调减小关系;入度-入度相关系数和出度-出度相关系数偏离0时,均使可控性指标nD不断增大;可控性指标与入度-出度相关系数没有关联.从图4和图5可知：双向网络作为一种特殊的有向网络,在边的重连变换下,网络可控性指标随着度相关系数(出度-入度、出度-出度、入度-入度和入度-出度相关系数)的增大均表现为逐步减小,并不完全遵循文献[2]的结论.

如何解释无向(或双向)网络的度相关性对可控性的这种影响规律呢?考虑到双向网络的四种度相关系数在边重连过程中是同步变化的,从图1出发我们尝试对四种度相关系数的影响效应做一个简单的平均.当平均度〈k〉≥5时,在各种度相关系数均接近于-1处,驱动节点在网络中所占的比例较大,网络最难达到可控;在各种度相关系数均接近于0处,驱动节点在网络中所占的比例应该较小;但是在各种度相关系数均接近于1处,驱动节点在网络中所占的比例应该介于前两者之间,这与图4的结果显然不相符,说明各种度相关系数对可控性的综合影响不能简单地看成各种度相关系数对可控性影响的简单平均.也就是说,虽然无向网络可以看作有向网络的特殊情况,但无向网络中的度相关性与可控性的关系有着特殊的规律,不能由有向网络中的度相关性与可控性的关系所直接反映.

对无向(或双向)网络的度相关性与可控性的关系,我们分三种情况做如下分析.

1)当各种度相关系数在0附近时,利用cavity方法可以分别推导出各种度相关系数对可控性指标所产生的影响[2].出度-入度相关系数r(out-in)对nD的影响(只计算展开到r(out-in)的一次项)为

其中M2(x)和H(α)(x)(α∈{in,out})的具体形式见文献[2],且H(α)(x)仅与度分布P(kin,kout)有关.因此,可控性指标近似为关于出度-出度相关系数r(out-out)的二次函数,且二次项系数为正.如果将有向网络中的所有边的方向都反转,则出度-出度关系恰变成入度-入度关系,而网络的结构可控性不变.这说明入度-入度相关系数对网络可控性的影响与出度-出度相关系数产生的影响一致,具体关系式与(10)式类似：可控性指标也近似为关于入度-入度相关系数r(in-in)的二次函数.由于的表达式不依赖于有向边起始节点的入度和末端节点的出度,因此,入度-出度相关系数r(in-out)对网络可控性没有影响,图1(b)中的数值模拟也表明了这一点[2].考虑到双向网络中因此双向网络的结构可控性指标nD是关于度相关系数r的函数,并且将函数nD关于变量r线性化后,r的一次项系数为负数.基于微扰的思想,在度相关系数r=0附近可以判断nD关于r是单调减小的.我们的解析分析结果与实验结果(图4和图5)一致.

2)当各种度相关系数较小且向-1靠近时,上述基于微扰的方法不再适用.由于入度-出度相关系数对网络可控性没有明显影响,这里只考虑其他三种度相关系数的影响.当各种度相关系数较小且向-1靠近时,由于入度-入度相关系数、出度-出度相关系数和出度-入度相关系数的减小对可控性指标均产生增大的作用,故最终的影响结果是随着各种度相关系数向-1靠近,可控性指标nD增大.这与我们实验的结果也保持一致.

3)当各种度相关系数较大且向1靠近时,可控性指标nD的基本变化趋势比较令人困惑,此时基于微扰的方法不适用,nD的变化趋势也不能从有向网络的各种度相关系数对可控性的影响简单地进行综合而推得.仅从实验的结果来看,在各种度相关系数对可控性的影响中,似乎是出度-入度相关系数对双向网络的可控性起了主导作用.导致该现象的原因可能是,双向网络的度相关系数接近于1时,网络中的大度值节点彼此相连容易形成边密度较大的点簇,这种内部大度值节点簇加上外围小度值节点的结构使得双向网络的匹配集更大,从而使其驱动节点比例下降.

综上可知,当网络度相关系数在0附近时,可控性指标单调减小;当度相关系数趋近于-1时,可控性指标趋于最大值;当度相关系数趋近于1时,可控性指标趋于最小值.因此,度相关系数由-1变为0的过程中,网络的可控性指标连续地逐渐减小;度相关系数由0变为1的过程中,网络的可控性指标继续逐渐减小或保持不增.

最后,我们从某些实际的网络出发,对上述度相关性对可控性的影响规律做进一步验证.这里采用的是网络理论与实验方面科学家们的合著关系网和美国西部的电网,它们分别来自文献[31,32].将这两个网络看作权值不确定的双向网络,可计算出网络的度相关系数和结构可控性指标如表1所示;网络的结构可控性指标随度相关性的变化如图7所示.可见,网络的结构可控性指标关于度相关系数单调减小,与理论模型中所反映的规律(图4和图5)一致.

图7 一般的有向边重连变换下,双向网络的度相关系数r对结构可控性指标nD(SCd)的影响 (a)网络理论与实验方面科学家们的合著关系网;(b)美国西部电网.图中结果来自50次独立模拟的平均,误差线表示标准偏差Fig.7.The impact of the degree correlation coefficientron the structural controllability measurenDfor bidirectional networks with rewiring of directed edges：(a)Co-authorship network of scientists in network theory and experiments;(b)the power grid of the western United States.Each data point is an average of 50 independent runs,and the error bars denote the standard deviations.

表1 两个实际网络的度相关系数r和结构可控性指标nD的计算值Table 1.Calculated values of the degree correlation coefficientrand the structural controllability measurenDfor the two real networks.

5 总 结

本文的研究对象主要是无向网络及对应的双向网络,其边权既可以是确定的也可以是未知的.实际上,我们的研究可以做进一步推广.对于更一般的有向网络,如果每个节点的出度与入度都相同,则该网络的四种度相关系数都相等,在边的重连变换过程中网络的各种度相关性也同步变化.通过类似的数值模拟发现,这种有向网络的可控性指标也是关于其度相关系数的减函数,并且与无向网络或双向网络中反映的规律(图4、图5和图7)高度地一致,而不完全遵循文献[2]中的规律(图1).

在不考虑网络的度相关性因素情况下,文献[3]通过大量数值模拟发现无自环的大型稀疏网络的严格可控性近似地与结构可控性一致.在此,我们通过数值模拟,进一步验证了对于无自环的大型稀疏网络,即使在同配或异配非常明显的情况下,网络的严格可控性与结构可控性的结果仍符合得很好.

通过数值仿真实验发现,无向网络及其推广网络的可控性指标是关于其度相关系数的减函数,即可控性指标随着度相关性的增大而减小.随后,我们对这种现象与有向网络中的情形做了对比和分析,并做出了部分解释,其中包括在度相关系数r=0附近的理论分析.虽然无向网络可以看作有向网络的特殊情况,但无向网络中的度相关性与可控性的关系有着特殊的规律,不能全部由有向网络中的度相关性与可控性的关系所直接反映.这一规律启示我们：对于无向网络及其推广网络,可以从度相关性角度去预测网络的可控性;增加网络的度相关性可能有助于减少驱动节点的数量,从而降低网络的控制难度.

虽然单一度相关性对网络可控性的影响已有较系统的阐述,但多种度相关性的共同作用对可控性产生的效应还不是很清楚.正如文献[2]所反映的,测量实际网络的度相关系数,并通过各种度相关系数对可控性的影响去综合分析和预测网络的可控性在多数情况下是有效的,但这种预测方法还有一定的局限性和片面性.本文以无向网络及其推广网络为研究对象,揭示了各种度相关系数同步变化对网络可控性的影响(可控性指标的变化规律).这里仍有一些需要继续探索的问题：无向网络的度相关系数接近于1时,为什么可控性指标变小?无向网络(或双向网络)的可控性随度相关性变化的内部机理是什么?另外,是否可以通过对其他特殊有向网络的探索来发现更多相关规律?相信对这一系列问题的探索将有助于人们理解各种度相关系数与网络可控性的更深层关系.

[1]Liu Y Y,Slotine J J,Barabási A L 2011Nature473 167

[2]Pósfai M,Liu Y Y,Slotine J J,Barabási A L 2013Sci.Rep.3 1067

[3]Yuan Z Z,Zhao C,Di Z R,Wang W X,Lai Y C 2013Nat.Commun.4 2447

[4]Zhou T,Zhang Z K,Chen G R,Wang X F,Shi D H,Di Z R,Fan Y,Fang J Q,Han X P,Liu J G,Liu R R,Liu Z H,Lu J A,Lü J H,Lü L Y,Rong Z H,Wang B H,Xu X K,Zhang Z Z 2014J.Univ.Electron.Sci.Technol.China43 1(in Chinese)[周涛,张子柯,陈关荣,汪小帆,史定华,狄增如,樊瑛,方锦清,韩筱璞,刘建国,刘润然,刘宗华,陆君安,吕金虎,吕琳媛,荣智海,汪秉宏,许小可,章忠志2014电子科技大学学报43 1]

[5]Ruths J,Ruths D 2014Science343 1373

[6]Wuchty S 2014Proc.Natl.Acad.Sci.U.S.A.111 7156

[7]Xu M,Xu C Y,Wang H,Deng C Z,Cao K F 2015Eur.Phys.J.B88 168

[8]Xu C J,Zheng Y,Su H S,Wang H O 2015Int.J.Control88 248

[9]Hou L L,Lao S Y,Xiao Y D,Bai L 2015Acta Phys.Sin.64 188901(in Chinese)[侯绿林,老松杨,肖延东,白亮2015物理学报64 188901]

[10]Nie S,Wang X W,Wang B H 2015Physica A436 98

[11]Ruths D,Ruths J 2016Sci.Rep.6 19818

[12]Kawakami E,Singh V K,Matsubara K,Ishii T,Matsuoka Y,Hase T,Kulkarni P,Siddiqui K,Kodilkar J,Danve N,Subramanian I,Katoh M,Shimizu-Yoshida Y,Ghosh S,Jere A,Kitano H 2016NPJ Syst.Biol.Appl.2 15018

[13]Kalman R E 1963J.Soc.Ind.Appl.Math.Ser.A1 152

[14]Lombardi A,Hörnquist M 2007Phys.Rev.E75 056110

[15]Lin C T 1974IEEE Trans.Autom.Contr.19 201

[16]Lovász L,Plummer M D 1986Matching Theory(Amsterdam：North-Holland)pp83-119

[17]Mézard M,Parisi G 2001Eur.Phys.J.B20 217

[18]Hautus M L J 1969Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen Ser.A72 443

[19]Wang X F,Chen G R 2002Physica A310 521

[20]Zhou M Y,Zhuo Z,Liao H,Fu Z Q,Cai S M 2015Sci.Rep.5 17459

[21]Zhou M Y,He X S,Fu Z Q,Liao H,Cai S M,Zhuo Z 2016Physica A446 120

[22]Orouskhani Y,Jalili M,Yu X H 2016Sci.Rep.6 24252

[23]Newman M E J 2002Phys.Rev.Lett.89 208701

[24]Foster J G,Foster D V,Grassberger P,Paczuski M 2010Proc.Natl.Acad.Sci.U.S.A.107 10815

[25]Newman M E J 2003Phys.Rev.E67 026126

[26]Maslov S,Sneppen K 2002Science296 910

[27]Hopcroft J E,Karp R M 1973SIAM J.Comput.2 225

[28]Qu J,Wang S J 2015Acta Phys.Sin.64 198901(in Chinese)[屈静,王圣军 2015物理学报 64 198901]

[29]Goh K I,Kahng B,Kim D 2001Phys.Rev.Lett.87 278701

[30]Kirkpatrick S,Gelatt Jr C D,Vecchi M P 1983Science220 671

[31]Newman M E J 2006Phys.Rev.E74 036104

[32]Watts D J,Strogatz S H 1998Nature393 440

Effect of degree correlations on controllability of undirected networks∗

Xu Ming1)2)3)Xu Chuan-Yun1)Cao Ke-Fei1)†
1)(Center for Nonlinear Complex Systems,School of Physics and Astronomy,Yunnan University,Kunming 650091,China)
2)(School of Mathematical Sciences,Kaili University,Kaili 556011,China)
3)(School of Mathematics and Statistics,Guizhou University of Finance and Economics,Guiyang 550025,China)

23 July 2016;revised manuscript

5 September 2016)

The controllability analysis of complex networks is of great importance for modern network science and engineering.Existing research shows that the controllability of a complex network is affected not only by the degree distribution of the network,but also by the degree correlation.Although the effect of degree correlations on the network controllability is well studied for directed networks,it is not yet very clear for the case of undirected networks.To explore the impact of degree correlations on the controllability of undirected networks and their corresponding generalized(bidirectional and directed)networks,in this paper,we use the simulated annealing algorithm to change the network degree correlation coefficients by link rewiring.First,the undirected Erdős-Rényi random network and the modified scale-free network are taken as example models to be investigated.Numerical simulations show that the controllability measure(density of driver nodes)of undirected networks decreases monotonically with the increase of the degree correlation coefficient under a constant degree distribution.Specifically,when the degree correlation coefficient changes from-1 to 0,the controllability measure decreases rapidly;while the decrease in the controllability measure is not obvious when the degree correlation coefficient changes from 0 to 1.Next,the bidirectional networks and some directed networks are considered;in these networks,the in-degree of each node is equal to its out-degree,thus link rewiring results in the simultaneous changes of various degree correlations(i.e.,in-in,in-out,out-in,and out-out degree correlations).Further investigations show that these bidirectional and directed networks also follow the above rule,which is verified by the two real networks.The increase of the degree correlation coefficient in undirected networks also implies the increases of various degree correlation coefficients in the corresponding directed networks.Although the effect of a single degree correlation on the controllability of directed networks is clear,the comprehensive effect of the simultaneous changes in various degree correlations on the network controllability cannot be additively and therefore directly estimated by the relevant results in the corresponding directed networks;namely,the effect of the degree correlation on the controllability in an undirected network has its special rule.Some explanations are given for this phenomenon.Moreover,for a large sparse network without self-loops,no matter how assortative or disassortative it is,its structural controllability and exact controllability are verified to be almost the same.These studies will deepen the understanding of the relationship between the network controllability and the network structure.

complex network,undirected network,controllability,degree correlationPACS:89.75.-k,89.75.Hc,02.30.Yy

10.7498/aps.66.028901

:89.75.-k,89.75.Hc,02.30.Yy DOI:10.7498/aps.66.028901

∗国家自然科学基金(批准号：11365023)、贵州省科技厅/黔东南州科技局/凯里学院科技联合基金(批准号：黔科合LH字[2014]7231)和贵州省教育厅优秀科技创新人才支持计划(批准号：黔教合KY字[2015]505)资助的课题.

†通信作者.E-mail：kfcao163@163.com

*Project supported by the National Natural Science Foundation of China(Grant No.11365023),the Joint Fund of Department of Science and Technology of Guizhou Province/Bureau of Science and Technology of Qiandongnan Prefecture/Kaili University,China(Grant No.LH-2014-7231),and the Science and Technology Talent Support Program of Department of Education of Guizhou Province,China(Grant No.KY-2015-505).

†Corresponding author.E-mail：kfcao163@163.com