基于Pancharatnam-Berry相位调控产生贝塞尔光束∗

陈欢 凌晓辉 何武光 李钱光 易煦农

1)(湖北工程学院物理与电子信息工程学院,孝感 432000)

2)(衡阳师范学院物理与电子工程学院,衡阳 421002)

基于Pancharatnam-Berry相位调控产生贝塞尔光束∗

陈欢1)凌晓辉2)何武光1)李钱光1)易煦农1)†

1)(湖北工程学院物理与电子信息工程学院,孝感 432000)

2)(衡阳师范学院物理与电子工程学院,衡阳 421002)

(2016年9月17日收到;2016年11月26日收到修改稿)

提出了一种基于Pancharatnam-Berry相位设计制作的超表面平面轴棱锥透镜产生贝塞尔光束的方法.理论分析表明：由于Pancharatnam-Berry相位的自旋相关性,设计的平面轴棱锥透镜需采用左旋圆偏振光入射才能有效地产生贝塞尔光束.超表面微结构单元的旋转率与最大无衍射距离成反比,这提供了一个获得更大无衍射距离的方便的途径.最后,搭建了一套基于平面轴棱锥透镜的贝塞尔光束产生系统,实验结果与数值模拟结果一致.这些结论有助于设计制作更多新颖的基于Pancharatnam-Berry相位的平面光子学器件.

贝塞尔光束,Pancharatnam-Berry相位,超表面

1 引 言

无衍射光束由于其独特的传输特性而一直备受关注[1].贝塞尔光束作为无衍射光束家族中的一员，最早由Durnin等[2]于1987年提出并在实验中观察到.贝塞尔光束除了具有在自由空间传输的无衍射特性之外,还有遇到障碍物光场自修复、中心光强极高等引人瞩目的传输特性.这些特性使得贝塞尔光束在微观粒子操控、激光加工、生物工程、高精度定位等领域具有重要的价值和广泛的应用前景[3-6].目前,研究人员已经开发出多种方法产生近似无衍射光场,如环缝-透镜法[2]、轴棱锥法[7,8]、谐振腔法[9]、计算机全息法[10]、透镜轴棱锥法[11]、双轴棱锥法等[12].

近年来,许多研究人员利用由人工设计的二维微结构阵列构成的超表面材料来实现对光波相位和偏振的控制.超表面作为一类缩减维度的超材料,相比体材料具有易于制作、应用方便、性能优良[13]等优点.尤其值得一提的是,超表面让我们能够采用平面光学元件对光波进行控制,从而使“平面光子学”成为可能[14,15].Hasman的研究小组[16]通过在介质基底或者金属薄膜上蚀刻亚波长光栅来操控CO2激光的偏振和相位.美国密歇根大学的Grbic小组[17]通过在金属膜上蚀刻不同形状的微结构构成超表面,对微波波前和偏振进行了一系列的操控研究.普渡大学的Shalaev小组[18]利用纳米天线阵列实现了宽带的光弯曲.哈佛大学的Yu等[19]基于金膜上蚀刻的天线阵列制作出了中红外波段的超表面四分之一波片.英国伯明翰大学的Zhang小组[20]利用C形天线阵列构成宽带超表面,同时实现了对电磁场振幅和相位的控制.目前,国内也有很多小组在进行基于超表面操控光场的相关研究,比如王慧田小组[21,22]、袁小聪小组[23].

本文研究利用基于Pancharatnam-Berry(PB)相位设计的超表面平面轴棱锥透镜来产生贝塞尔光束.Pancharatnam-Berry相位是一类与光场偏振态改变有关的几何相位,具有自旋相关的特性.飞秒激光可以在石英硅玻璃中诱导产生的形式双折射(form birefringence),双折射的大小可以通过激光的强度和偏振等进行控制.在玻璃中按事先设计好的空间分布写入微纳米量级的波片(微结构)实现对光束横截面内偏振的操控,从而使光场获得所需的空变Pancharatnam-Berry相位[24-26].理论和实验研究表明,我们设计的超表面平面轴棱锥透镜能将左旋圆偏振入射光转化为近似无衍射贝塞尔光束.

2 理论分析

传统的轴棱锥透镜能将入射光场转化为贝塞尔光束是因其厚度沿径向变化,当光场通过它会获得一个径向变化的相位,而超表面通过控制其微结构单元的几何形状与空间分布理论上可以使入射光场获得任意相位[27].在本研究中,我们采用在石英硅玻璃中写入微纳米波片对光场偏振态进行操控,从而使入射光场获得想要的Pancharatnam-Berry相位.

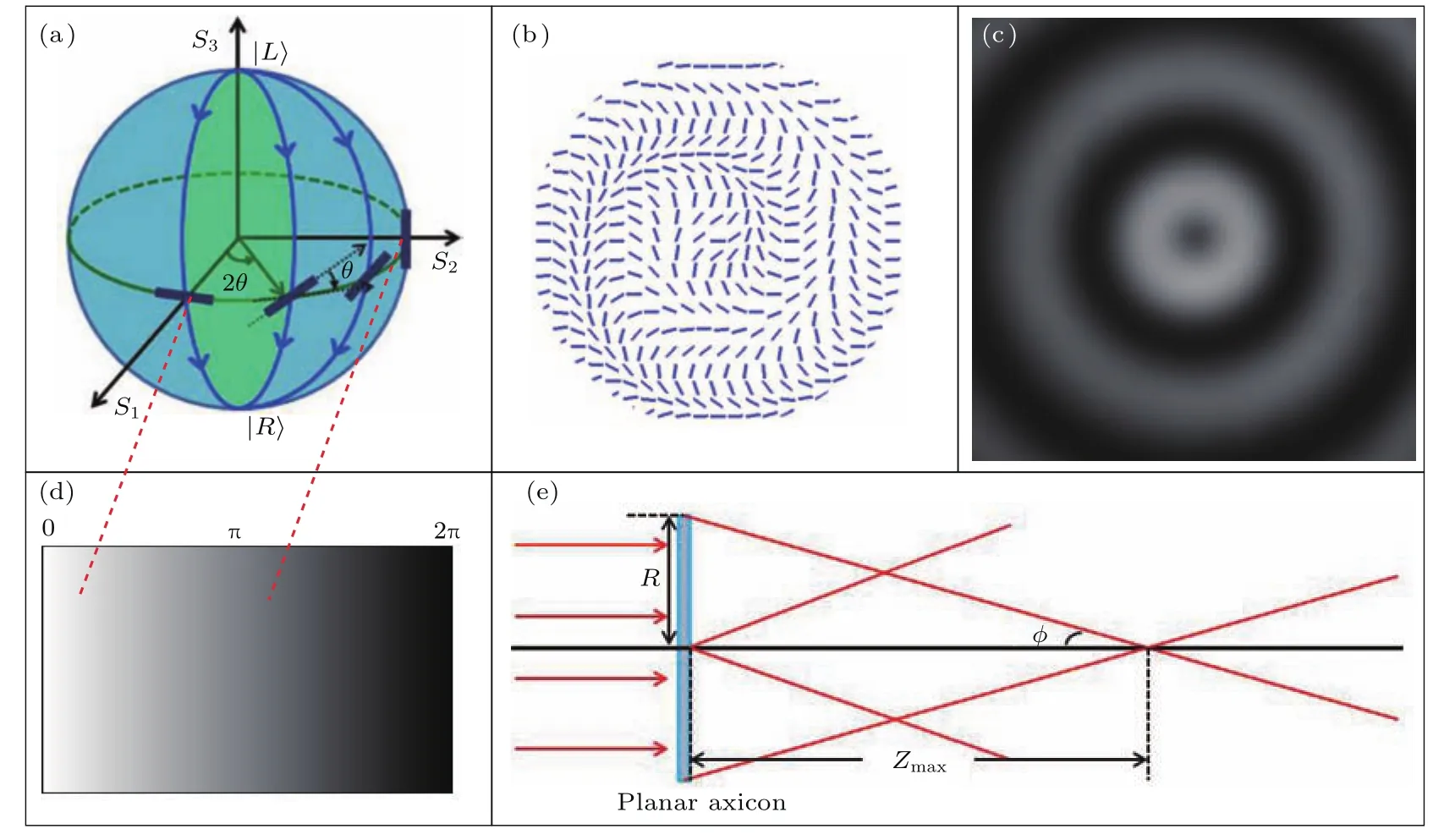
图1 (网刊彩色)(a)庞加莱球;(b)基于超表面的平面轴棱锥透镜慢轴分布示意图;(c)平面轴棱锥透镜的交叉偏振图;(d)0—2π的相位灰度图;(e)光波经平面轴棱锥透镜折射示意图Fig.1.(color online)(a)The Poincaré sphere;(b)the slow axis spatial distribution of the planar axicon;(c)the cross-polarized optical image of the planar axicon;(d)the grayscale image of 0-2π phase;(e)optical pathway diagram of light wave passing the planar axicon.

我们在超表面中写入的微纳米波片相位延迟为π,经过简单的运算可以得到其传输矩阵可以表示为

其中θ为超表面局域慢轴方向与x轴的夹角.考虑入射光场为圆偏振态,那么光场的琼斯矢量可以表示为

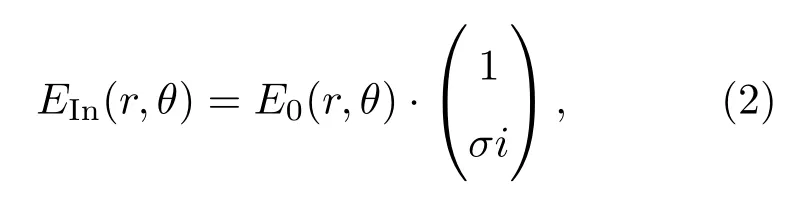
其中E0(r,θ)为光场振幅,σ=±1,+,-分别代表左、右旋圆偏振光.(1)式和(2)式结合可得超表面的输出光场为

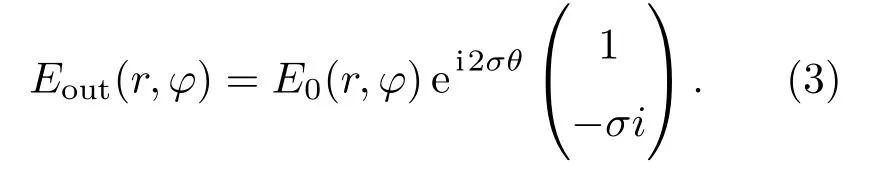
我们注意到输出光场除了圆偏振手性发生了反转之外,还获得了一个附加相位

这一附加相位就是Pancharatnam-Berry相位[28].Pancharatnam-Berry相位的大小及分布完全由超表面的微结构局域光轴方向决定.同时,值得注意的是,Pancharatnam-Berry相位的符号取决于入射场的偏振手性,或者说 Pancharatnam-Berry相位是自旋相关的.总而言之,控制超表面局域光轴的角度θ和入射光场的偏振手性即能获得想要的Pancharatnam-Berry相位.

众所周知,庞加莱球是一个描述光场偏振态演化的几何表象.利用庞加莱球也可以方便直观地看出偏振态演化所产生的Pancharatnam-Berry相位.图1(a)给出了超表面局域光轴不同角度所对应的偏振态演化.当左旋圆偏振光入射到慢轴方向为水平方向的半波片时,光在波片中的偏振态将沿庞加莱球的0◦经线演化;而当半波片的慢轴方向为垂直方向时,光在波片中的偏振态将沿庞加莱球的90◦经线演化.当光场的偏振态演化在庞加莱球上形成闭合曲线时,闭合曲线围成的面积所对应的曲面的立体角的1/2即为光场偏振态演化所产生的Pancharatnam-Berry相位.

由以上分析可知,要使入射光场获得与传统轴棱锥透镜相同的径向变化相位,超表面的慢轴分布需要遵循以下表达式：

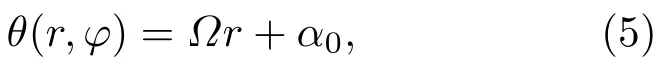
其中Ω=π/d为局域慢轴的旋转率,d为周期,α0为初始光轴方向.图1(b)给出了基于超表面的平面轴棱锥透镜慢轴分布示意图,图1(c)为超表面的交叉偏振图.

图1(e)给出了平面波入射到平面轴棱锥透镜的几何光路图.光波经过平面轴棱锥透镜后会发生与传统棱锥透镜类似的折射,在其后的光场交叠区域形成无衍射贝塞尔光束.根据图中简单的几何关系,可以得到贝塞尔光束的最大无衍射距离为

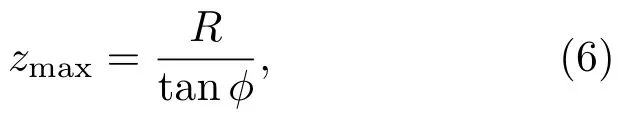
其中R为平面轴棱锥透镜的半径,φ为光场经过平面轴棱锥透镜的折射角,且

Δk为折射光横向波矢分量,k0为光场在自由空间中的波数.横向波矢分量Δk由光场从平面轴棱锥透镜获得的相位梯度决定.结合(4)式,可以得到

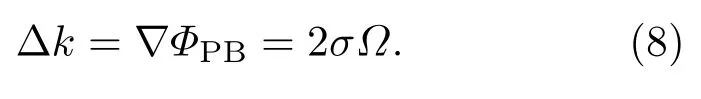
联合(7)式和(8)式,我们还会发现一个光场经过平面轴棱锥透镜是发散还是聚焦取决于入射光场的偏振手性.如果入射光场为左旋圆偏振,则折射光场是汇聚的,在平面轴棱锥透镜后光场交叠区域会产生贝塞尔光束.当入射光场为右旋圆偏振,折射光场会是发散的,平面轴棱锥透镜后不存在类似传统轴棱锥透镜的光场交叠区域,故不能产生贝塞尔光束.简言之,由于Pancharatnam-Berry相位的自旋相关性,采用慢轴分布满足(5)式的平面轴棱锥透镜产生贝塞尔光束,入射光场必须为左旋圆偏振光.考虑到这一条件后,结合(7)式和(8)式,可以将(6)式改写为

我们知道,采用传统轴棱锥透镜产生贝塞尔光束,其最大无衍射距离与轴棱锥透镜底角成反比,也就是说,轴棱锥透镜底角越小则产生的贝塞尔光束无衍射距离越长.然而,需要指出的是,底角越小加工越困难,成本也必然越高.同时,角度过小时,在加工轴棱锥透镜时很容易产生误差,最终导致所产生的光束产生畸变.这里需要特别指出的是,采用平面轴棱锥透镜不会遇到这样的困难.从(9)式中可以看到,贝塞尔光束的最大无衍射距离反比于平面轴棱锥透镜微结构单元的旋转率Ω,所以,我们可以通过降低微结构单元的旋转率即可获得更大的无衍射距离,从而也可以避免加工传统轴棱锥透镜底角过小时遇到的技术难题.假设入射光为左旋圆偏振高斯光束.在傍轴条件下,结合(3)式和(5)式,平面轴棱锥透镜后沿z轴传输的输出光场可以用菲涅耳衍射积分表示为

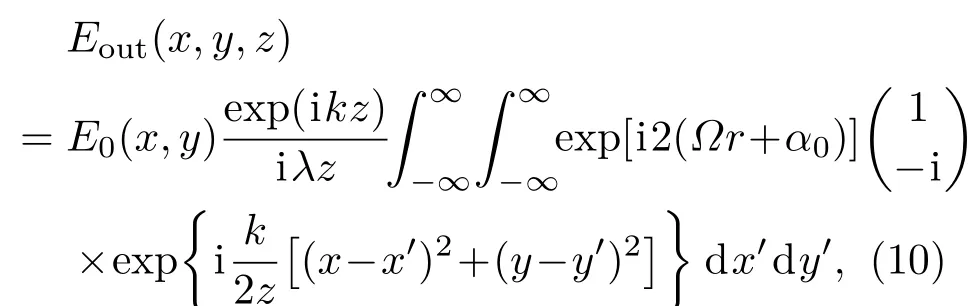
基于(10)式,我们对左旋圆偏振高斯光束经过平面轴棱锥透镜后进行了数值模拟.图2为平面棱锥透镜后不同距离处的光强分布.图2(a)—(d)显示光束中心光强极强而光束旁瓣很弱,并且在传输过程中光斑图样基本保持不变,所以,从模拟结果可以看出,利用平面棱锥透镜能够产生近似无衍射贝塞尔光束.

图2 数值模拟平面轴棱锥透镜后不同距离处的光强分布 (a)z=10 cm;(b)z=40 cm;(c)z=70 cm;(d)z=100 cmFig.2.The simulated intensity distribution behind the planar axicon with different distance：(a)z=10 cm;(b)z=40 cm;(c)z=70 cm;(d)z=100 cm.

3 实验结果

图3为我们采用的实验装置示意图.波长为632.8 nm的He-Ne激光通过望远镜准直系统扩束后入射到由一个格兰激光偏振镜(GLP)和一个四分之一波片(QWP)组成的偏振控制系统.格兰激光偏振镜和四分之一波片快轴成45◦以获得左旋圆偏振光,左旋圆偏振光再入射到平面轴棱锥透镜.最后,用CCD相机记录平面轴棱锥透镜输出的光强分布.实验中采用的超表面平面棱锥透镜其微结构旋转周期d为1000µm,平面轴棱锥透镜的半径R为5 mm.根据(6)式可知,平面轴棱锥透镜产生的贝塞尔光束理论最大无衍射距离可达7.9 m.众所周知,当采用传统的轴棱锥透镜要获得较大无衍射距离时,需要加工出底角足够小的轴棱锥透镜.需要再次强调的是：利用平面轴棱锥透镜产生贝塞尔光束其最大无衍射距离反比于微结构的旋转率.所以,我们可以通过降低微结构的旋转率来增加最大无衍射距离.相比于传统的轴棱锥透镜方法,平面轴棱锥透镜方法在技术上更加容易实现大的无衍射距离,这也是平面轴棱锥透镜产生贝塞尔光束的优势之一.

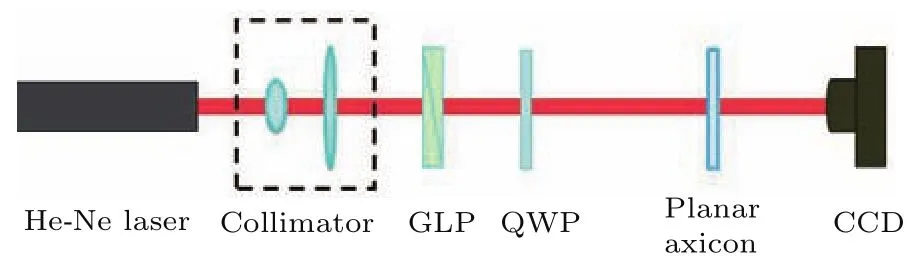
图3 基于平面轴棱锥透镜产生贝塞尔光束实验装置图(GLP,格兰激光偏振镜;QWP,四分之一波片)Fig.3.Diagram of the experimental setup for generating Bessel beams based on planar axicon(GLP,Glan laser polarizer;QWP,quarter-wave plate).

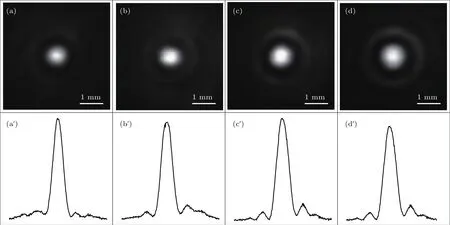
图4 实验测得的平面轴棱锥透镜后不同距离处的光强分布 (a)—(d)距离分别为10,40,70和100 cm处的横向光强分布;(a′)—(d′)为相应的径向光强分布图Fig.4.The measured intensity distribution behind the planar axicon with different distance：(a)-(d)The intensity distribution in cross section with transmission distance 10,40,70 and 100 cm,respectively;(a′)-(d′)the corresponding intensity distribution in radial direction.

图4为平面轴棱锥透镜后不同距离处的光强分布.图4(a)—(d)分别为距离10,40,70和100 cm处的横向光强分布.图4(a′)—(d′)分别为对应的径向光强分布.我们看到平面轴棱锥透镜后光束能保持横截面光强分布不随传输距离的增加而发生变化,而且光束中心光强极高,这正与无衍射贝塞尔光束的特征符合.将图4与图2的数值模拟结果比较也可看到,实验结果与仿真模拟的结果一致.这证明我们采用平面轴棱锥透镜能有效地产生贝塞尔光束.

4 结 论

本文提出了一种基于Pancharatnam-Berry相位产生贝塞尔光束的方法.我们基于Pancharatnam-Berry相位设计制作了一片超表面平面轴棱锥透镜作为产生贝塞尔光束的核心器件.我们首先通过理论分析得出：由于Pancharatnam-Berry相位的自旋相关性,采用超表面平面轴棱锥透镜产生贝塞尔光束,其入射光必须为左旋圆偏振光.尤其值得一提的是,利用平面轴棱锥透镜产生贝塞尔光束其最大无衍射距离反比于微结构的旋转率,这意味着可以通过降低微结构的旋转率方便地获得较大的无衍射距离.随后,基于菲涅耳衍射积分,我们通过数值模拟的方法得到了平面轴棱锥透镜后不同距离处的光场分布.数值模拟表明左旋圆偏振高斯光束入射到平面轴棱锥透镜后,出射光束随传输距离的变化保持中心光强极强而旁瓣较弱的光斑图样,具备贝塞尔光束的无衍射特征.最后,我们采用微结构旋转周期d为1000µm的超表面搭建了一套基于平面轴棱锥透镜的贝塞尔光束产生系统,实验结果与数值模拟结果一致.所以,基于平面轴棱锥透镜能够有效地产生近似无衍射的贝塞尔光束.这一研究有助于开发、设计出更多基于Pancharatnam-Berry相位的平面光子器件.

[1]Bouchal Z,Wagner J,Chlup M 1998Opt.Commun.151 207

[2]Durnin J,Miceli J J,Eberly J H 1987Phys.Rev.Lett.58 1499

[3]McGloin D,Dholakia K 2005Contemp.Phys.46 15

[4]Zhao L,Wang F,Jiang L,Lu Y,Zhao W,Xie J,Li X 2015Chin.Opt.Lett.13 041405

[5]Cai Y,Lv X 2007Opt.Commun.274 1

[6]Chen B,Pu J 2009Chin.Phys.B18 1033

[7]Scott G,McArdle N 1992Opt.Eng.31 2640

[8]Sun Q,Zhou K,Fang G,Liu Z,Liu S 2012Chin.Phys.B21 014208

[9]Wu F,Chen Y,Guo D 2007Appl.Opt.46 4943

[10]Turuenen J,Vasara A,Friberg A T 1988Appl.Opt.27 3959

[11]Sochacki J,Kolodziejczyk A,Jaroszewicz Z,Bara S 1992Appl.Opt.31 5326

[12]Zheng W T,Wu F T,Zhang Q A,Cheng Z M 2012Acta Phys.Sin.61 144201(in Chinese)[郑维涛,吴逢铁,张前安,程治明2012物理学报61 144201]

[13]Kildishev A V,Boltasseva A,Shalaev V M 2013Science339 1232009

[14]Li X,Pu M,Zhao Z,Ma X,Jin J,Wang Y,Gao P,Luo X 2016Sci.Rep.6 20524

[15]Ke Y,Liu Y,Zhou J,Liu Y,Luo H,Wen S 2016Appl.Phys.Lett.108 101102

[16]Bomzon Z,Biener G,Kleiner V,Hasman E 2001Opt.Lett.26 33

[17]Pfeiffer C,Grbic A 2013Phys.Rev.Lett.110 197401

[18]Ni X,Emani N K,Kildishev A V,Boltasseva A,Shalaev V M 2012Science335 427

[19]Yu N,Aieta F,Genevet P,Kats M A,Gaburro Z,Capasso F 2012Nano Lett.12 6328

[20]Liu L,Zhang X,Kenney M,Su X,Xu N,Ouyang C,Shi Y,Han J,Zhang W,Zhang S 2014Adv.Mater.26 5031

[21]Kang M,Guo Q,Chen J,Gu B,Li Y,Wang H 2011Phys.Rev.A84 045803

[22]Kang M,Chen J,Wang X,Wang H 2012J.Opt.Soc.Am.B29 572

[23]Lin J,Wang Q,Yuan G,Du L,Kou S S,Yuan X 2015Sci.Rep.5 10529

[24]Yi X,Ling X,Zhang Z,Li Y,Zhou X,Liu Y,Chen S,Luo H,Wen S 2014Opt.Express22 17207

[25]Beresna M,Gecevičius M,Kazansky P G,Gertus T 2011Appl.Phys.Lett.98 201101

[26]Liu Y,Ling X,Yi X,Zhou X,Luo H,Wen S 2014Appl.Phys.Lett.104 191110

[27]Yi X,Liu Y,Ling X,Zhou X,Ke Y,Luo H,Wen S,Fan D 2015Phys.Rev.A91 023801

[28]Courtial J 1999Opt.Commun.171 179

PACS:42.25.—p,42.25.Ja,03.65.Vf DOI:10.7498/aps.66.044203

Generation of Bessel beam by manipulating Pancharatnam-Berry phase∗

Chen Huan1)Ling Xiao-Hui2)He Wu-Guang1)Li Qian-Guang1)Yi Xu-Nong1)†
1)(College of Physics and Electronic Information Engineering,Hubei Engineering University,Xiaogan 432000,China)
2)(College of Physics and Electronic Engineering,Hengyang Normal University,Hengyang 421002,China)

17 September 2016;revised manuscript

26 November 2016)

Bessel beam is one of diffraction-free beams and has some peculiar properties.Varieties of its applications have been found,such as microparticle manipulating,material processing and biological studies.In this work,we propose a method of creating a Bessel beam by manipulating Pancharatnam-Berry phase.Using femtosecond laser,nano waveplatelets are written on a fused silicon glass to form a metasurface.The optical axis of waveplatelets rotating in the radial direction can produce the space-varying Pancharatnam-Berry phase.The designed metasurface acts as a planar axicon to generate Bessel beams by replacing the traditional one.A Jones calculation is employed to analyze the transformation of the metasurface.The theoretical results indicate that a left-handed circularly polarized light passing through the planar axicon is convergent,while a right-handed circularly polarized one is divergent.The intrinsic physical reason is that Pancharatnam-Berry phase is spin-dependent.Therefore,Bessel beams are generated by the planar axicon only when a left-handed circularly polarized light inputs the system.It is notable that the maximum nondiffracting distance is determined by the rate of rotation of the metasurface microstructure.By reducing the rate of rotation,we can easily obtain a longer nondiffracting distance,thus avoiding the problem that the base angle of the traditional axicon is too small to fabricate.According to the Fresnel diffraction integral,we simulate the propagation of the field emerging from the planar axicon and obtain the intensity distributions behind the planar axicon with different distances.The results show that the intensity pattern remains unchanged in the propagating process and possesses the propagation properties of Bessel beam.It implies that approximate nondiffraction Bessel beams can be achieved by employing the planar axicon with metasurface.Finally,we set up an experimental system with the Pancharatnam-Berry phase metasurface with periodd=1000µm to verify the theoretical analysis.Theoretically,the maximum nondiffraction distance is 7.9 m.In the shaded region,we measure the intensity distributions at different distances.The experimental results are in good agreement with the simulation results,so the planar axicon based on Pancharatnam-Berry phase can be an effective Bessel beam generator.We believe that these results are helpful for developing more spin-dependent photonic devices.

Bessel beam,Pancharatnam-Berry phase,metasurface

:42.25.—p,42.25.Ja,03.65.Vf

10.7498/aps.66.044203

∗国家自然科学基金(批准号：11547017,11547018)、湖北省教育厅科学研究项目(批准号：B2015031)和特色果蔬质量安全控制湖北省重点实验室开放基金(批准号：2016K01)资助的课题.

†通信作者.E-mail：xnyi@szu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11547017,11547018),the Foundation of Hubei Educational Committee,China(Grant No.B2015031),and the Foundation of Hubei Key Laboratory of Quality Control of Characteristic Fruits and Vegetables,China.

†Corresponding author.E-mail：xnyi@szu.edu.cn