表面缺陷的方向性对漏磁场分布的影响∗

吴德会 刘志天 王晓红 苏令锌

(厦门大学航空航天学院,厦门 361005)

表面缺陷的方向性对漏磁场分布的影响∗

吴德会 刘志天 王晓红†苏令锌

(厦门大学航空航天学院,厦门 361005)

(2016年7月20日收到;2016年11月1日收到修改稿)

由于漏磁检测(MFL)具有操作简单、成本低廉、信号稳定等特点,已被广泛应用于铁磁材料的无损检测.在MFL领域,实现缺陷评估的关键是对漏磁信号与缺陷几何特征之间的关系进行准确描述.本文建立了一个任意方向的表面缺陷漏磁场分布的三维数学模型.首先,将表面缺陷近似为一个有限长的矩形槽来进行描述;然后,从理论上分析了不同缺陷方向下槽壁磁荷密度的变化规律;最后,通过矢量合成得到了有向缺陷的漏磁场分布.开展了仿真和实验,对缺陷在不同磁化方向下的漏磁场分布进行了分析.实验结果表明,缺陷的MFL分布与方向性密切相关.随着与磁化方向夹角增大,缺陷漏磁场水平分量亦增加,单峰性也越突出;但垂直分量却随夹角的增大而呈现双峰分布.所建模型能有效地描述缺陷的方向性对漏磁场分布影响,对优化MFL检测器设计和提高缺陷评估质量有实际指导意义.

漏磁检测,磁偶极子,裂纹,表面缺陷方向性

1 引 言

在现代工业中,大量的铁磁性金属构件,如管道、桥梁、铁路、汽轮机叶片、转子、起重机等承载件和焊接部件等,因老化、腐蚀、疲劳等原因造成的缺陷极易导致事故的发生.漏磁检测(magnetic flux leakage,MFL)技术作为一种传统的电磁无损检测方法,具有无污染、不需耦合剂、快速、高可靠性等优点,被广泛应用于铁磁材料的无损检测领域[1].

利用MFL方法对缺陷进行评估,需要建立漏磁场分布与缺陷特征之间的对应关系.目前,国内外对缺陷漏磁场模型的研究方法主要有磁偶极子法(magnetic dipole method)和有限元法(finite element method,FEM).Zatsepin和Shcherbinin[2]首次提出了矩形缺陷的二维无限磁偶极子模型,为缺陷的磁偶极子理论奠定了基础.Wu等[3]利用二维磁偶极子模型探究了不同磁化方向、裂纹方向下的漏磁场分布规律,为二维磁偶极子模型的工程应用提供了理论指导.王朝霞等[4]通过二维磁偶极子模型推导出弱磁场作用下管道细长裂纹上的磁场法向分量计算公式.汪滨波等[5]给出了圆柱铁磁构件的漏磁模型的二维磁偶极子解析式,并通过实验论证了该解析式的正确性,对2D磁偶极子理论模型提供了有力支撑.在利用有限元仿真解决实际工程问题的研究方面,国内外学者也同样活跃.Yong等[6]建立三维有限元仿真模型,并融合采集到的漏磁场三个分量信息,最终实现了任意形状裂纹的检测.Wu等[7]对TMR检测器的参数进行了有限元仿真优化设计,并根据仿真参数设计实际实验,能够探测到0.3 mm直径的细小圆缺陷.刘保余和綦耀光[8]对周向励磁下的漏磁检测进行参数化的有限元仿真,结果证实了周向励磁方法检测轴向缺陷的可行性,该结论具有一定的工程实用价值.杜志叶等[9]建立了静态和瞬态漏磁场有限元仿真模型,并比较了两种模型的仿真结果和效率,给出了静磁场分析钢管缺陷漏磁场应满足的条件.

在上述的磁偶极子法的漏磁场描述中,往往是将有向缺陷(如裂纹)近似为一个无限长且垂直于磁化方向的矩型或环型凹槽,这样可利用无限长磁偶极线来简化模型,从而求解缺陷的2D漏磁场分布.随着对缺陷漏磁理论研究的不断深入,关于缺陷漏磁的磁偶极子3维分析研究也已开展.Zhang等[10]基于有限长磁偶极子模型,提出了一种缺陷的重建方法,并给出了不同提离值情况下的重建结果.Mandache和Clapham[11]计算了单个圆柱形缺陷的表面漏磁场,并在此基础上对缺陷之间漏磁场的相互作用展开了研究.廖昌荣等[12]建立了V形裂纹的三维磁偶极子模型,并通过实验验证了模型的有效性,该模型可用于裂纹几何参数的估计.刘美全等[13]以三维离散磁偶极子模型为基础实现了缺陷的断层成像,为缺陷的三维重构提供了新思路.

在实际MFL检测的工程应用中,有向缺陷的方向往往是任意的,因此其与磁化方向的夹角也是随机的.实际工程应用表明,即使是相同几何形状的缺陷,其方向差异也会造成截然不同的漏磁场分布.目前,关于缺陷漏磁场分布的机理研究,均是假设缺陷方向与磁化方向平行或垂直.而关于任意磁化方向下有向缺陷的三维磁偶极子模型研究,国内外尚未见文献报道.本文着力于一个任意磁化方向下有限长缺陷的三维磁偶极子建模研究,分析缺陷的特征对漏磁场分布的影响规律,并在形式上统一了对长缺陷(如裂纹等)和短缺陷(腐蚀坑等)的磁偶极子模型描述.研究结果不但可丰富、完善缺陷表面漏磁场的磁偶极子建模理论,而且对设计有效的MFL检测器及缺陷形态反求也具有实际的指导意义.

2 槽形截面漏磁场的二维磁偶极子模型

磁偶极子理论认为缺陷的漏磁场可由极性相反的偶极子相互作用来进行解释.所谓磁偶极子是指一对异种等量磁荷组成的磁性体系.若被测的铁磁性材料表面或近表面存在缺陷,对该材料进行磁化时,沿磁化方向的缺陷两侧会有磁力线泄漏.在磁通离开的缺陷一侧和进入的缺陷一侧形成有效的磁极.该磁极可近似由一对极性相反的等量磁荷(即磁偶极子模型)来进行模拟.

为方便分析,往往将有向缺陷(如裂纹)假设为无限长且垂直于磁化场B方向的矩形槽.铁磁材料磁畴的自发磁化则以磁荷形式均匀分布在槽的两壁,磁荷面密度可记为σx,两壁磁荷符号相反.此时,可忽略有向缺陷长度的影响,而建立如图1中所示的二维磁偶极子模型.

图1 矩形槽二维磁偶极子截面图Fig.1.Cross-section of rectangular groove under 2D magnetic dipole model.

图1所示的截面图中,矩形槽的宽度为2b,深度为h.以缺陷中心为原点,以磁化方向为X轴,可建立平面笛卡尔坐标系X-Y.则在此坐标系下,两个槽壁上的微线元dξ在场点P(x,y)点处产生的磁场强度dH1,dH2可分别表示为

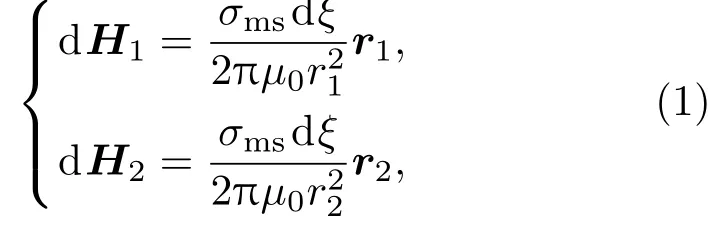
式中,µ0为真空磁导率,r1和r2为场点P相距正负磁荷线的距离.

若记微线元dξ到材料表面的距离为ξ,则距离两槽壁微线元dξ产生磁场强度的大小在X-Y坐标系中表示为

其中,dH1x,dH2x为两槽壁微线元在P点产生的磁场强度X分量;dH1y,dH2y为两槽壁微线元在P点产生的磁场强度Y分量.将上式沿槽壁深度h进行积分,即可得到两槽壁在场点P(x,y)处形成漏磁场的X-Y轴分量Hx与Hy的大小：

根据磁偶极子模型的原理,σms的取值可通过下式进行计算[14]：

式中,µ为被测材料的相对磁导率,H0为外加磁场强度大小.

设有一个无限长的垂直缺陷,其宽度2b为1 mm,深度h为1 mm,提离值y设为1 mm,外加激励磁场强度H0大小取180 A·m-1,钢板的相对磁导率µ取2000.把上述参数代入(3)式所示的二维磁偶极子模型中,沿X轴从-20到20 mm分别取值计算漏磁场的X,Y分量大小Hv和Hp,结果如图2所示.

图2 (网刊彩色)垂直缺陷漏磁场的二维磁偶极子建模结果Fig.2.(color online)Calculation results of MFL signal for a perpendicular defect by means of 2D magnetic dipole model.

这里的二维磁偶极子模型的槽形截面为矩形,实际上还可以将该槽形截面近似为梯形、V形、半椭圆形等.槽形不同主要表现在磁偶极子沿深度积分上的差异,其模型本质上并无不同.

3 任意磁化方向下有限长缺陷的三维磁偶极子模型

3.1 任意方向磁化场与缺陷的作用关系

无论槽形截面的形状是梯形、V形还是矩形,其二维磁偶极子模型均是建立在无限长和垂直于磁化方向这两个假设的基础之上,因此该模型只能作为实际缺陷分析的定性参考.而实际无损检测应用中,被测材料中缺陷的方向往往是未知的,即其与磁化方向的夹角θ具有随机性.缺陷与磁化场的相对方向是影响其漏磁场分布的重要因素.因此本文利用磁偶极子的基本原理,建立一个可以描述缺陷方向信息的三维磁偶极子模型.

在本文模型中,不再假设有向缺陷垂直于磁化方向.若缺陷与磁化场具有方向上的任意性,那么其与磁化方向必然支起一个三维有限空间,因此上文中缺陷无限长的假设也必然不再成立.这里仍以槽形截面为矩形的案例进行建模,讨论矩形槽对任意方向外磁场作用下的漏磁场分布,对于其他槽形截面可同理分析,限于篇幅,本文不再赘述.

由于被测材料表面内缺陷与磁化方向夹角θ具有任意性,因此需要建立一个固定的坐标系描述缺陷.不失一般性,以材料表面上的缺陷中心为原点,材料表面的外法向为Y轴,缺陷方向为Z轴,建立空间笛卡尔坐标系,如图3所示.

图3 平面内三维矩形槽的坐标示意Fig.3.Schematic diagram of a 3D rectangular groove.

如图3中,沿矩形槽三个正交方向建立坐标轴x,y,z,并给出其长、宽和深度分别为2Dx,Dy和2Dz.假设外磁场H0沿任意方向(平行于XOZ与缺陷方向夹角记为θ.由于MFL检测中,磁化场H0平行于被测材料表面,因此磁化场H0与缺陷的空间关系如图4(a)中所示.

图4 任意方向磁化场与缺陷关系示意 (a)磁化场及其正交分解;(b)正交磁化场对缺陷的作用Fig.4.Schematic diagram of defect and magnetizingfield in arbitrary direction：(a)Magnetizing field and its orthogonal decomposition;(b)impact of orthogonal magnetizing field on the defect.

可对磁化场H0进行矢量分解,将其分解为与缺陷方向平行和垂直的两个向量H0,Z和H0,X,即有

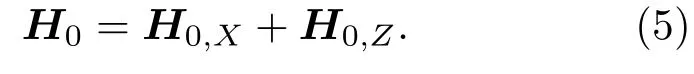
因此,任意方向磁化场H0的作用,可以理解为两个正交磁化场H0,X和H0,Z对有向缺陷作用的叠加.则正交磁化场H0,X和H0,Z与缺陷的关系如图4(b)所示.

3.2 任意磁化方向下有限长缺陷磁场的建模及矢量合成

从图4(b)中可以看出,磁化场H0,X与缺陷横向的两个槽壁是垂直的,而磁化场H0,Z与缺陷纵向的两个槽壁是垂直的.因此,可将平行于xoz面的磁场分解为平行于x轴和平行于z轴的磁场分量来分析,然后再根据磁场叠加原理,将二者矢量结果求和来获得任意磁场对有限长缺陷的作用,进而获得有限长缺陷的漏磁场分布.

图5 横向槽面磁极微面元的磁场分布Fig.5.Magnetic field distribution of magnetic microsurface on transverse groove face.

在漏磁检测过程中,该铁磁性材料已经磁化至近饱和状态,材料内部磁通趋于饱和且分布均匀,此时,槽壁上的磁荷密度亦呈相对均匀分布.不妨先分析磁化场H0,X对缺陷的作用,如图5所示,可设H0,X对横向槽壁上形成的磁荷面密度为σx.则定义三维空间场点的坐标为P(x,y,z),磁荷面源点的坐标为(xm,ym,zm).则磁核面上的微面元dymdzm在空间场点P产生的磁场强度表示可为

图5中槽面在X轴上的位置为xm,其外形为有限矩形,范围在Y轴从0到-Dy,在Z轴从-Dz到Dz.则根据图5中所示的坐标关系,对该槽面进行二元积分,得到该矩形槽面在场点P(x,y,z)处形成的漏磁场HX在三个坐标轴方向的分量大小分别为

对上式积分运算进行求解,可以得到更直观的低等表达式为

磁化场H0,X对缺陷产生的漏磁场分布HX,实际为xm=-Dx处的正磁极子和xm=Dx的负磁极子的合成磁场.因此,H0,X在场点P(x,y,z)处产生的漏磁场向量HX为

ex,ey,ez分别为三维坐标轴X,Y,Z三个方向的单位向量.同理,磁化场H0,Z与缺陷纵向两个槽壁是垂直的,可在纵向槽壁上形成σz的磁荷面密度,则该槽壁微面元dxmdym在空间中产生的磁场强度分布如图6所示.

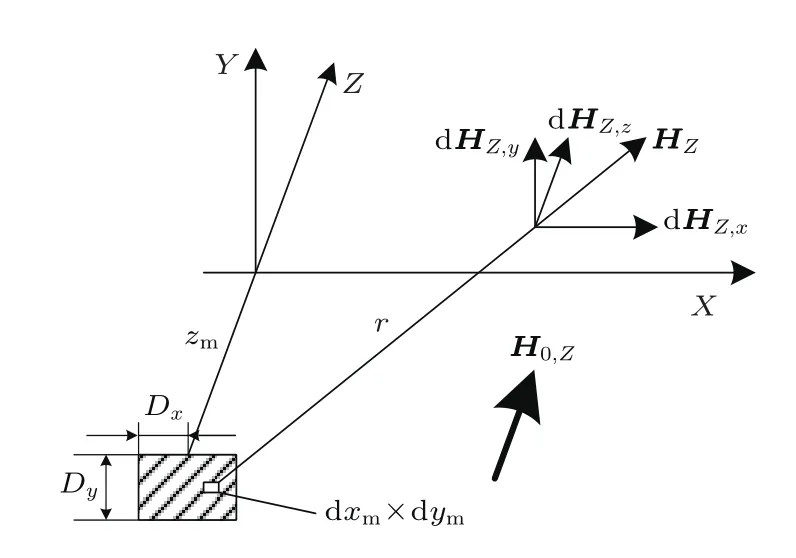
图6 纵向槽面磁极微面元的磁场分布Fig.6.Magnetic field distribution of magnetic microsurface on longitudinal groove face.

图6中矩形槽面范围在X轴从-Dx到Dx,在Y轴从0到-Dy.同样,可记该槽面在Z轴上的位置为zm.则可由图5的坐标关系对槽面进行二元积分,得到槽面在任意场点P(x,y,z)处形成的漏磁场分布：

上式积分运算求解过程与(8)式相似,限于篇幅度,本文不再列出.很明显,磁化场H0,z对缺陷的影响,可表示为zm=-Dz处的正磁极子和zm=Dz的负磁极子的合成.因此,H0,Z在任意位置点P(x,y,z)处产生的漏磁场向量HZ为

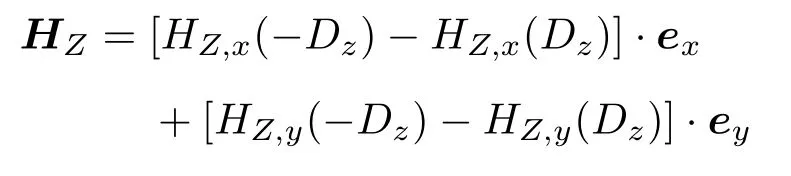
对于磁化场H0可分解为与缺陷方向相关的两个正交向量H0,X和H0,Z,缺陷槽壁在两正交方向上形成的磁荷密度σx和σz可参考(4)式进行计算.同样,在场点P(x,y,z)处总的漏磁场/分布则可通过HX和HZ进行矢量合成得到：

由上式可以看出,通过正交磁化场的三维空间的磁偶极子建模及矢量合成,可以实现对任意磁化场下的有限长表面缺陷漏磁场分布的机理分析.

4 模型分析

4.1 有限长缺陷的漏磁场分布

为分析本文所建任意方向有限长缺陷的三维磁偶极子模型,首先设计一个宽度2Dx=2 mm,深度Dy=2 mm的缺陷.外加磁化场强度H0取180 A·m-1,磁化方向与缺陷方向垂直,即夹角θ=90◦.钢板的相对磁导率µ取2000.漏磁场检测的提离值y设为1 mm,并设置扫查路径为沿X轴-20—20 mm范围,即z=0 mm,x=-20—20 mm.利用本文所提模型求解长度2Dz从1—8 mm变化的缺陷中心漏磁场分布,即取z=0.其与(3)式求解无限长缺陷漏磁场的结果对比如图7所示.

从图7中可以看出,当缺陷与磁化方向垂直时,缺陷的漏磁场分量Hx和Hy均随缺陷长度增加而增大.而且,当缺陷长度2Dz→∞时,本文所提方法与现有2维磁偶极子模型完全符合[15].从图7中的计算结果来看,当缺陷长度Dz＞5Dx时,缺陷中心处的漏磁场Hx和Hy形态已与2维磁偶极子模型计算结果相差无几.

再设置缺陷长度2Dz从2—20 mm变化.扫查路径设置为在缺陷正上方沿z方向从-20—20 mm范围,即x=0 mm,z=-20—20 mm.提取扫查路径上漏磁场的X分量,其结果如图8所示.

在图8中,漏磁场扫查曲线从内到外分别对应长度为2,4,6,···,20 mm 的缺陷.由于2维磁偶极子模型是将缺陷假设为无限长,该模型在Z方向上无分析能力,因此在图8中表现为一条水平线.虽然,较长缺陷(Dz＞5Dx)的漏磁场无限接近于2维磁偶极子模型,但也只是在Z轴的中间部分近似为水平.在缺陷两端仍会呈现明显的梯度下降,并迅速收敛为0,本文称为边缘效应.因此,在垂直磁化条件下,2维磁偶极子模型仅限于对较长缺陷中间部分的近似,而在缺陷两端5Dx范围内,由于受边缘效应的影响,2维模型将不再适用.

图7 (网刊彩色)不同长度缺陷引发漏磁场的X轴方向扫查结果 (a)漏磁场X分量;(b)漏磁场Y分量Fig.7.(color online)Scanning for defects of different lengths along thex-axis：(a)Xcomponent of MFL signal;(b)Ycomponent of MFL signal.

图8 (网刊彩色)不同长度缺陷引发漏磁场的Z方向扫查结果Fig.8.(color online)Scanning for defects of different lengths along thez-axis.

4.2 长缺陷的方向性与漏磁场的关系

通过上节的分析可知,对垂直于磁化方向的长缺陷(Dz＞5Dx),其中心漏磁场分布可近似利用2维磁偶极子模型进行描述.那么,与磁化方向含有一定夹角θ的长缺陷,中心漏磁场分布又会有怎样的变化,是否仍能用2维磁偶极子模型进行描述,则有待进一步研究.

图9 不同方向缺陷引发漏磁场的磁化方向扫查结果 (a)漏磁场X分量;(b)漏磁场Y分量;(c)漏磁场Z分量Fig.9.Scanning for defects of different angles along the magnetizing direction：(a)Xcomponent of MFL signal;(b)Ycomponent of MFL signal;(c)Zcomponent of MFL signal.

在上述缺陷中,取定缺陷长度为10 mm,并将缺陷在磁化场中旋转,当然也可理解为缺陷固定,磁化场旋转.缺陷与磁化场的夹角θ从0到π/2变化,每隔10◦旋转一个角度.考虑到实际工程应用的具体情况,在分析过程中沿磁化方向设置扫查路径L,扫查范围在-20— 20 mm,即L=-20—20 mm,z=Lcosθ,x=Lsinθ. 则利用本文所建模型分别计算该缺陷在不同方向(角度)时的漏磁场分量Hx,Hy和Hz,其结果如图9所示.

从图9中可以看出,由于缺陷与磁化方向夹角θ的差异,对于同一个缺陷,其产生的漏磁场信号也截然不同.在图9(a)中,随着夹角θ从0◦—90◦变化,漏磁场X分量Hx的幅度逐渐增大.而且,随着Hx幅度增大的同时,Hx信号的有效宽度也明显变窄,单峰性更加突出.对比之下,漏磁场Y分量Hy随夹角θ的变化更为复杂,其信号峰值并不随着夹角θ单调变化.如图9(b)中所示,Hy形成了两个峰值集中区,一个对应X轴为主磁化方向,另一个对应以Z轴为主磁化方向时.随角度变化,两个峰值集中区之间此消彼长,而在过渡部分,即θ=30◦—40◦左右时,Hy同时受到X和Z两个方向边缘效应的影响,因此其幅值相对较小.但是无论哪个磁化方向,Hy均有较明显信号输出.

如图9(c)中所示,缺陷漏磁场Z分量Hz的幅度要明显小于Hx和Hy,且其随着夹角θ变化规律也与Hx相反,呈单调递减趋势.当θ=90◦时,漏磁场无Z向分量,即Hz=0.需要注意的是,在Hz波形中的中间部分,当θ＜40◦时,还出现了明显的凹陷而呈双峰分布.

图10 (网刊彩色)不同方向缺陷的中心处漏磁场强度Fig.10.(color online)Leakage magnetic field intensity on the center of a defect with different magnetizing angles.

为进一步研究有限长缺陷中心处漏磁场与磁化方向θ之间的关系,我们分别取漏磁场的X,Z两分量作为检测结果进行观察.有限长缺陷中心处的漏磁场大小Hmaxx,Hmaxz与缺陷方向之间的关系,如图10中所示.

从图10中可以清晰地看出,Hmaxx和Hmaxz随磁化夹角θ的呈现清晰的单调性变化.因此,即使是对较长缺陷中间部分的漏磁场进行描述,只要该缺陷与磁化方向存在非正交关系,则不能使用传统的2维磁偶极子模型进行描述.

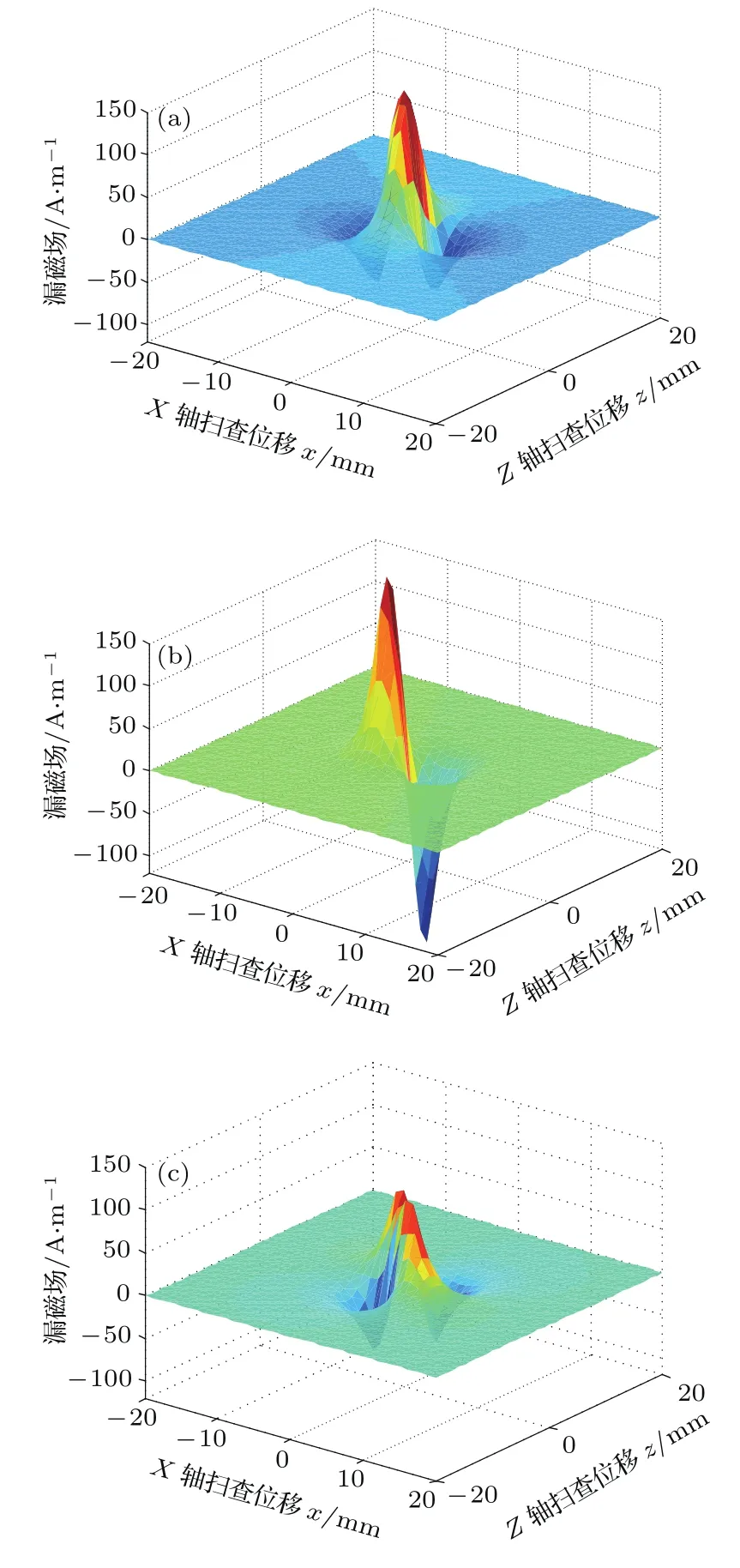
图11 (网刊彩色)斜向磁化短缺陷时引发漏磁场的三维分布 (a)漏磁场X分量;(b)漏磁场Y分量;(c)漏磁场Z分量Fig.11.(color online)Three-dimensional distribution of leakage magnetic field for a short defect under oblique-magnetization：(a)Xcomponent of MFL signal;(b)Ycomponent of MFL signal;(c)Zcomponent of MFL signal.

4.3 短缺陷的漏磁场分布

在MFL检测中,除了长缺陷(如裂纹)外,另一类典型表面缺陷是方向性不明显的腐蚀坑[16].对于自然形成的腐蚀坑,仍可以将其近似为长宽较接近的矩形凹槽,并利用本文所提模型进行描述.为便于统一描述,不失一般性,本文统称之为短缺陷.

设在上述磁化条件下,存在一个长度2Dz=4 mm,宽度2Dx=4 mm,深度Dy=2 mm的短缺陷.设置缺陷Z轴方向与磁化场的夹角θ=60◦,则利用本文磁偶极子模型,可绘制该缺陷漏磁场X,Y,Z分量Hx,Hy和Hz的三维云图,如图11所示.

很明显,该缺陷的开口为方型,并没有明显的方向性.因此,其漏磁场同时具有比较明显的X轴和Z轴分量Hx和Hz,如图11(a)和图11(c)所示.而且,磁化场与缺陷Z轴方向的夹角θ=60◦,因此缺陷漏磁场Z轴分量比X轴分量要相对弱一些.缺陷漏磁场的Y轴分量Hy同时受到X轴和Z轴磁泄漏的影响,因此如图11(b)所示,Hy的分布方向介于X轴和Z轴,基本和磁化场方向一致.上述这些特点,都与腐蚀坑MFL检测的实验经验相符合,本文所提方法可以较好描述地此类缺陷的漏磁场分布.

5 实验验证

首先,验证上面讨论的槽形截面二维磁偶极子模型的有效性.选用长度为500 mm,宽度为300 mm及厚度10 mm的钢板作为被测对象.通过机械加工的方法在钢板表面加工一条长形豁口以模拟现实中的裂纹缺陷.该裂纹的长度100 mm,宽度2b=4 mm和深度h=2 mm.通过MFL检测小车对钢板上的裂纹进行扫查,实验平台如图12所示.

MFL检测小车的磁化场由U形磁轭产生,磁轭的励磁线圈分别安装在两个磁极上,并采用双线圈对称性结构.励磁线圈使用1 mm的漆包线绕制100匝,并由直流电源RXN3010A提供1 A的驱动电流.霍尔元件选用高灵敏度的模拟型G1322,水平和重直两个方向安装于U形磁轭中间,并与钢板保持1 mm的提离值.首先将检测小车置于裂纹左侧,小车行进方向与裂纹垂直.进行MFL扫查时,检测小车从左向右运动,通过USB2832型A/D数据采集卡记录漏磁场的水平和垂直分量Hx和Hy的检测电压Ox和Oy,结果如图13所示.

图12 (网刊彩色)MFL测试平台及检测小车Fig.12.(color online)Testing platform and vehicle system of MFL.

图13 垂直裂纹扫查的漏磁场信号Fig.13.MFL scanning results for a perpendicular defect.

从图中漏磁场Hx和Hy的检测结果可以看出,实测信号的分布特征与理论分析结果(如图2中所示)基本符合.这说明对于横向的裂纹,利用二维磁偶极子模型进行描述确是可行的.

接下来,通过物理实验验证缺陷的方向性对漏磁场分布的影响规律.在钢板中心再加工一个长缺陷,其长、宽、深分别为40,3和2 mm.将霍尔元件固定于长缺陷的中心处,并与钢板保持1 mm的提离,用于采集中心处的漏磁场强度.实验中,将U形磁轭置于缺陷上方,并顺时针方向旋转磁轭,从而改变对长缺陷的磁化方向,其旋转过程如图14(a)所示.

图14 (网刊彩色)不同磁化方向的MFL实验 (a)磁化场旋转示意图;(b)缺陷的中心处MFL输出与磁化方向的关系Fig.14.(color online)MFL experiments with different magnetizing directions：(a)Diagrammatic sketch of rotating process of magnetizing field;(b)impact of defect orientation on leakage magnetic field intensity.

由于磁轭只是围绕缺陷旋转,整个旋转过程中磁化场的强度是保持不变的,仅仅是缺陷的方向角θ在改变.因此,可通过霍尔元件方便地拾取不同磁化方向角θ下,漏磁场的X,Z两分量,其检测结果如图14(b)所示.与图10中的模型计算结果进行对比可以看出,实测信号的分布特征与理论分析是一致的.当然,由于实测缺陷的长度更大,因此,Hz的检测值幅度相对略小些.

再将磁轭装配在行进小车上,并在磁轭正中心安装一个可水平旋转的螺旋套筒.霍尔元件装配于螺旋套筒上,并可360◦自由旋转.设置行进小车的扫查路径与缺陷的方向θ从0◦到80◦变化,每隔20◦扫查一次.扫查时,通过螺旋套筒调整霍尔元件的检测面始终与缺陷方向平行,即检测缺陷漏磁场的X分量.通过USB2832数据采集卡记录不同扫查方向θ下霍尔元件的输出电压Ox,检测结果如图15(a)所示.

再调整霍尔元件的检测面与缺陷方向垂直(即检测缺陷漏磁场的Z分量),重复上述实验,记录的霍尔元件输出电压Oz随扫查方向θ的变化规律如图15(b)所示.由于小车行进过程中不可避免地会产生振动,因此实际检测信号中包含了一定的噪声[17,18].但与图9中相应曲线进行对比可以看出,本文所提模型的分析结果与实验测试值的基本分布特征是符合的.因此,利用本文方法对任意方向有限长缺陷的漏磁场分布进行三维磁偶极子建模.

图15 不同扫查角度下的漏磁场检测结果 (a)漏磁场X分量检测输出;(b)漏磁场Z分量检测输出Fig.15.MFL signal when scanning along different directions：(a)Xcomponent of MFL signal;(b)Ycomponent of MFL signal.

6 结 论

1)实际MFL检测的工程应用中,缺陷是有限长的且具有方向性,现有的MFL分布模型对这种方向性无描述能力.本文通过三维磁偶极子理论,对一个任意方向有限长缺陷的MFL分布进行建模研究,该模型可有效分析缺陷的方向性对MFL分布的影响规律.

2)现有的2维磁偶极子模型仅限于在垂直磁化条件下对5倍宽度以上长缺陷的中间部分进行近似,而对于缺陷两端5倍宽度以内,受到边缘效应的影响,MFL将呈现明显的梯度下降,2维模型不再适用.

3)缺陷的MFL分布与方向性密切相关.随着夹角θ从0◦到90◦变化,漏磁场X分量的幅度逐渐增大.而且,MFL信号的有效宽度也明显变窄,单峰性更加突出.而漏磁场Z分量的幅度要明显小于X分量,且其随着夹角θ变化单调递减趋势.

4)缺陷漏磁场Y分量最方向性的影响更为复杂,该信号峰值并不随着夹角θ单调变化,而是形成两个峰值集中区,并随夹角θ变化,两个峰值集中区之间此消彼长.

5)所提模型还可对方向性不明显的短缺陷的MFL进行描述,并在形式上统一了对长缺陷(如裂纹等)和短缺陷(腐蚀坑等)的磁偶极子模型描述.

该项目得到了“福建省高端装备制造协同创新中心”的大力支持并提供了相关条件,在此表示感谢!

[1]Wu D H,Huang S L,Zhao W,Xin J J 2009Acta Petrol Sin.30 136(in Chinese)[吴德会,黄松岭,赵伟,辛君君2009石油学报30 136]

[2]Zatsepin N N,Shcherbinin V E 1966Defektoskopiya5 50

[3]Wu J,Sun Y,Kang Y,Yang Y 2015MAG IEEE Trans.Mechatron.51 1

[4]Wang C X,Zhang W M,Song J G,Li W C,Chen K 2007J.Beijing Inst.Technol.27 395(in Chinese)[王朝霞,张卫民,宋金刚,李文春,陈克2007北京理工大学学报27 395]

[5]Wang B B,Liao C R,Han L,Xie Y S,Shi X C 2011Chin.J.Sens.Actuat.24 238(in Chinese)[汪滨波,廖昌荣,韩亮,谢云山,石祥聪2011传感器技术学报24 238]

[6]Yong L,Wilson J,Gui Y T 2007NDT&E Int.40 357

[7]Wu B,Wang Y J,Liu X C,C F He 2015Smart.Mater.Struct.24 075007

[8]Liu B Y,Qi Y G 2010J.Shenyang Univ.Technol.32 187(in Chinese)[刘保余,綦耀光2010沈阳工业大学学报32 187]

[9]Du Z Y,Ruan J J,Yu S F,Liu B 2007Proc.Chin.Soc.Electr.Eng.27 108(in Chinese)[杜志叶,阮江军,余世峰,刘兵2007中国电机工程学报27 108]

[10]Zhang Y,Ye Z F,Wang C 2009NDT&E Int.42 369

[11]Mandache C,Clapham L 2003J.Phys.D:Appl.36 24

[12]Liao C R,Liao Z,Han L,Wang B B,Shi X C,Xie Y S 2012J.Chongqing Univ.35 76(in Chinese)[廖昌荣,廖峥,韩亮,汪滨波,石祥聪,谢云山 2012重庆大学学报 35 76]

[13]Liu M Q,Xu Z S,Wang J B 2005Chin.Mech.Eng.16 952(in Chinese)[刘美全,徐章遂,王建斌 2005中国机械工程16 952]

[14]Xu Z S,Xu Y,Wang J B 2005Quantitative Detection Principle and Application ofCrack in MFL Method(Vol.1)(Beijing：National Defend Industry Press)p124(in Chinese)[徐章遂,徐英,王建斌2005裂纹漏磁定量检测原理与应用(上卷)(北京：国防工业出版社)第124页]

[15]Edwards C,Palmer S B 1986J.Phys.D:Appl.Phys.19 657

[16]Liu J J,Sun J J,Hu H Y,Xing X S 2005Acta Phys.Sin.54 2414(in Chinese)[刘晶晶,孙俊君,胡海云,邢修三2005物理学报54 2414]

[17]Wu D H,Liu Z L,Zhang Z Y,Xia X H 2013J.Basic Sci.Eng.21 1188(in Chinese)[吴德会,柳振凉,张忠远,夏晓昊2013应用基础与工程科学学报21 1188]

[18]He Y Z 2013Acta Phys.Sin.62 084105(in Chinese)[何永周2013物理学报62 084105]

PACS:81.70.Ex,03.50.—z,52.70.Ds DOI:10.7498/aps.66.048102

Mechanism analysis of influence of surface-breaking orientation on magnetic leakage field distribution∗

Wu De-HuiLiu Zhi-Tian Wang Xiao-Hong†Su Ling-Xin

(School of Aerospace Engineering,Xiamen University,Xiamen 361005,China)

20 July 2016;revised manuscript

1 November 2016)

Magnetic flux leakage(MFL)has been widely applied to the nondestructive testing(NDT)of ferromagnetic materials due to its simple operation,low cost,and steady signal.Its defects are evaluated based on the relationship between MFL signal and the geometrical characteristic of defect.In this paper,a three-dimensional(3D)mathematical model is developed for the magnetic leakage field of surface-breaking defects that are arbitrarily oriented inside ferromagnetic material.Firstly,a finite-length rectangular slot is used as a simplified and convenient representation of a surface-breaking defect.Then,the magnetic charge densities of slot walls in different surface-breaking orientations are analyzed theoretically.The distribution of the magnetic leakage field can ultimately be derived by vector synthesis.Both simulations and experiments are conducted to analyze the magnetic leakage field distributions in different magnetization orientations.The results show that with increasing the angle between the defect orientation and the magnetic field,the horizontal component of the leakage magnetic field increases as demonstrated by increasing the prominence of its single peak.At the same time,however,the vertical component shows a bimodal distribution.The proposed model can effectively describe the influence of defect orientation on MFL signals,which can offer practical guidelines for optimizing MFL detectors and improving defect assessment.

magnetic flux leakage,magnetic dipole,crack,surface-breaking orientation

:81.70.Ex,03.50.—z,52.70.Ds

10.7498/aps.66.048102

∗国家自然科学基金(批准号：51177141,51677158)资助的课题.

†通信作者.E-mail：wxh@xmu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.51177141,51677158).

†Corresponding author.E-mail：wxh@xmu.edu.cn