基于彭罗斯拼图的部分随机复杂网络的统计性质*
2017-08-01傅秀军彭彩霞段雪晴
傅秀军 彭彩霞 段雪晴
(华南理工大学 物理与光电学院, 广东 广州 510640)
基于彭罗斯拼图的部分随机复杂网络的统计性质*
傅秀军 彭彩霞 段雪晴
(华南理工大学 物理与光电学院, 广东 广州 510640)
为扩展复杂网络模型并探讨网络的新特征,研究了随机复杂网络的统计性质.在以两种菱形为结构单元的彭罗斯拼图的基础上,增加顶点的随机连接,其连接概率与顶点的类型有关,由此构造出部分随机的复杂网络.用解析和数值方法计算了网络的主要特征参数.结果表明:度分度、节点间平均距离和网络集群系数与一般随机网络接近,但具体变化规律有所不同.由此可见,准周期复杂网络既有一般网络的共性,也有更为丰富的其他特征.
彭罗斯拼图;准周期结构;复杂网络;统计性质
复杂网络的研究从传统的规则图形开始,发展出ER随机网络[1- 2]、WS小世界网络[3- 4]、BA无标度网络[5- 6]等各种模型,揭示了理论上和现实中丰富的网络性质.1960 年,Erdos和Rényi为了描述通信和生命科学中的网络,根据随机图理论提出了随机拓扑模型来研究复杂网络[1- 2],发现了随机网络具有小集群系数、小平均距离的特征.之后的研究进一步证明了随机网络的度分布是泊松分布[7].然而实验研究发现,自然界中许多复杂网络的统计性质并不同于规则网络和随机网络,真实网络大都具有大的集群系数和小的平均距离等统计特征.因此,Watts等[3- 4]提出了描述现实网络的小世界网络模型.Barabási等[5- 6]提出了无标度网络模型,其节点度服从幂函数分布[7- 9],能反映许多真实网络的性质.
复杂网络在传统的研究中均基于图论,而初期的图论专注于一些规则图形,其中最具代表性的是二维周期结构,比如正方、三角和六角格子等,这与传统的固体物理主要研究周期晶体相类似.然而自从1984年准晶体在实验中被发现后[10],对准周期结构的研究也引起了人们的广泛关注[11- 15],特别是彭罗斯拼图(Penrose tiling)[16- 18].作为二维准晶的典型模型,其成功地描述了准晶结构,被广泛地应用于准晶体物理性质的研究中.准周期结构与周期结构都是规则的,最大不同在于准周期结构在任何尺度上都不会简单重复,且具有分形系统类似的自相似性.
将准周期结构应用于复杂网络,探讨其新的特性,是一项有意义的工作.文中从彭罗斯拼图出发,构造复杂网络,在原有的准周期结构上增加随机连接,其连接概率取决于节点的类型,研究由此演化出的网络的统计性质.
1 彭罗斯拼图的基本性质及网络模型的构造
彭罗斯拼图是最早用来描述二维准晶体结构的几何模型,它具有晶体点阵的长程有序性,但不具备平移对称性[19].彭罗斯拼图由两种基本单元组成,一种是锐角为72°的胖菱形,另一种是锐角为36°的瘦菱形,如图1(a)所示.在完整的彭罗斯拼图中,顶点类型共有8种,按照de Bruijn的叫法,这8种顶点分别称为S、 K、 Q、D、 J、 S3、 S4和S5[20],如图1(b)所示.
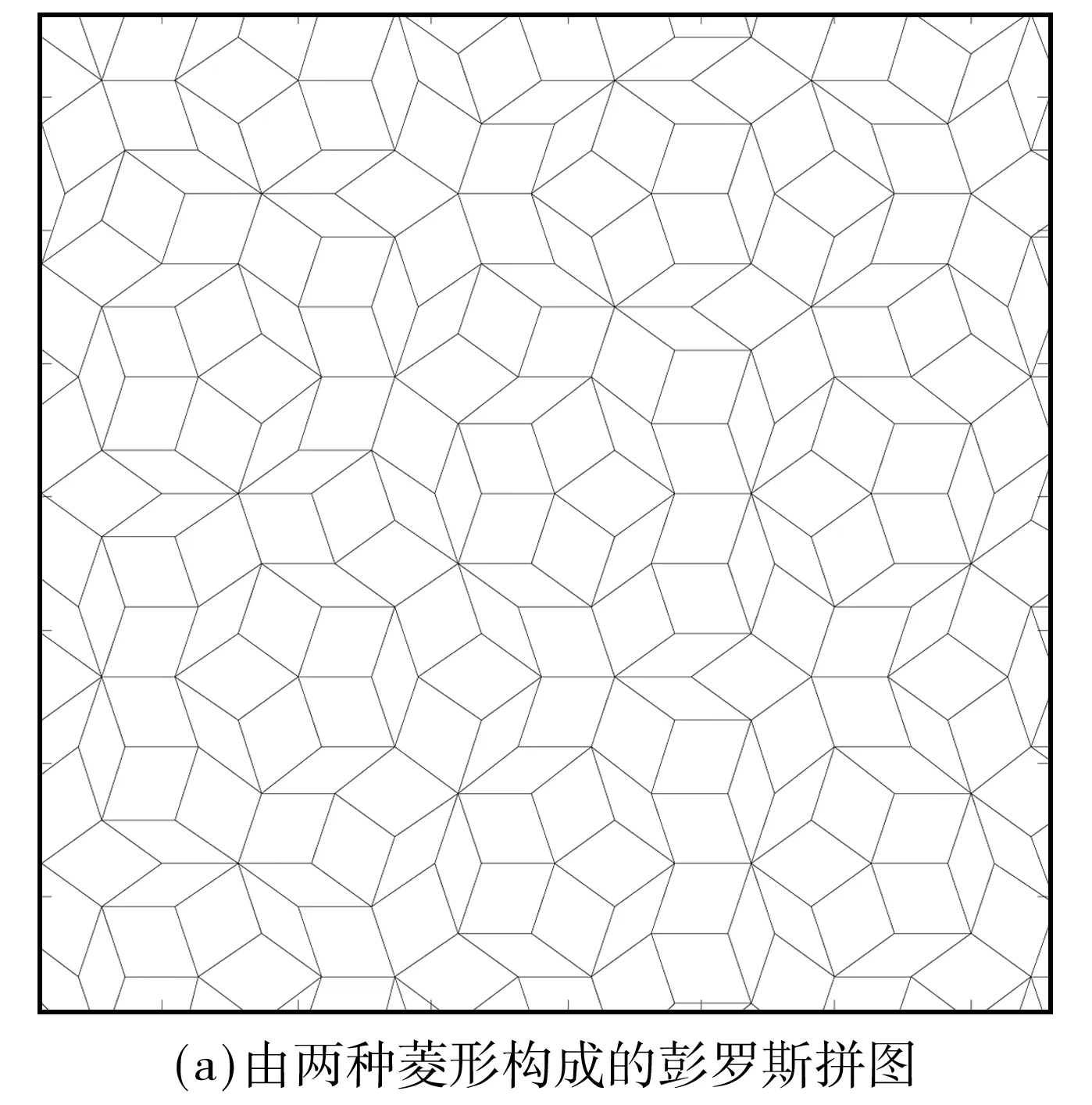

图1 由两种菱形构成的彭罗斯拼图及其8种顶点
Fig.1 Penrose tiling composed of two kinds of rhombi and its eight types of vertex
为了简便,将这8种顶点分别记作a、b、c、d、e、f、g和 h.在无限大彭罗斯拼图中,这8种顶点所占比例q(·)分别为[21]
(1)

构造随机复杂网络模型一般是先给出一定数目的节点,然后各节点之间以一定概率随机连接,图2是将10个节点随机连接的示意图.若直接将彭罗斯拼图中的顶点看作网络的节点,菱形边看作连边,则为准周期规则网络.在已有菱形边连接的基础上,文中根据顶点类型引入随机连接,则可构造出部分随机的复杂网络模型.基本构造思想是:同种类型顶点间的连接概率为p1,不同种类型顶点间的连接概率为p2,不考虑距离的限制.由此构造出的模型突破了原来彭罗斯拼图的局域性限制,更接近于众多的实际复杂网络.

图2 10个节点随机连接构成的复杂网络Fig.2 A complex network randomly connected by 10 nodes
2 网络的度分布性质
由彭罗斯拼图的顶点性质可知,若没有额外的连接,网络节点的度只有k=3,4,5,6,7这5种情况.对应于彭罗斯拼图中顶点c和d的度为3,顶点b的度为4,顶点a、e和h的度为5,顶点g的度为6,顶点f度为7.因此,若不考虑边界效应,规则彭罗斯网络的度分布情况为
(2)
当增加了顶点的随机连接,且同类间连接与不同类间连接概率p1与p2相差较大时,网络的度分布会有明显的变化.首先给出数值计算结果,如图3所示,分别为p1=0.8、p2=0.2和p1=0.2、p2=0.8的情况.

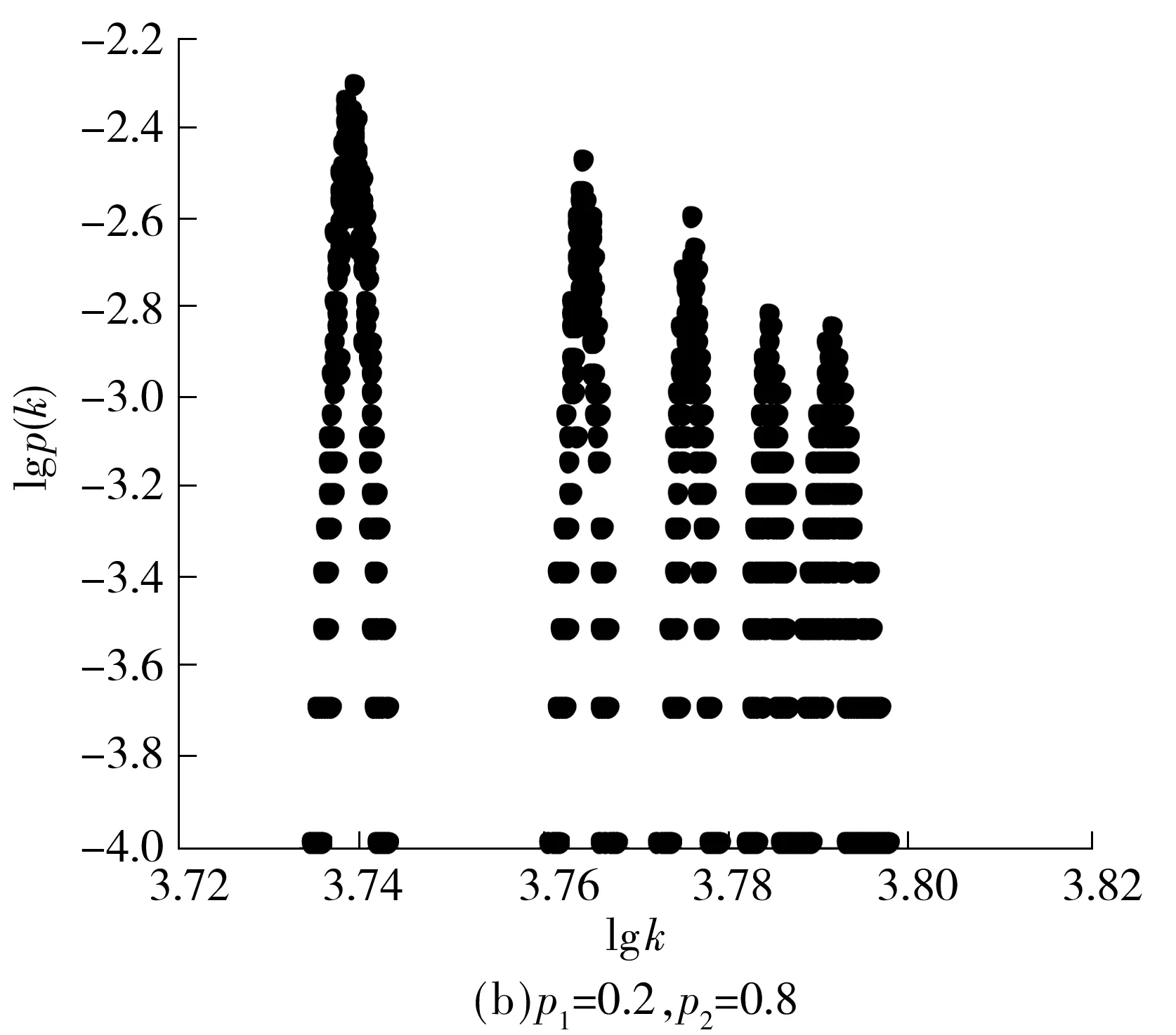
图3 网络的度分布Fig.3 Degree distribution of the networks
研究发现,在以上两种网络中,度分布函数均出现5个峰值,围绕每个峰值的度分布均类似于小世界随机网络.当p1≫p2时,度平均值大的峰值较高;当p1≪p2时,度平均值大的峰值较低.考虑到此网络是按照8种顶点类型以一定规律连接而构造的,出现5个峰值的原因应该是某些构型的度简并.为了探究这个问题,将各个类型顶点的度分开进行统计,结果发现,最小平均度的节点是来源于4种顶点(a、f、 g和 h)的贡献,它们各自形成独立的峰,位置基本上是重叠的,如图4所示.第i类顶点的数目Ni与度分布的关系可分析如下:当p1≫p2且Ni较大时,则大部分i类节点都相连,而i类与其他类型的节点连接概率小.所以节点i的度很大程度上由同种类型连接度决定,不同种类型节点连接度有一定的调节作用.这样导致该类型度分布在较小的范围内,且大于其他节点类型对应的的度分布概率.设Ni、Nj为任意两种节点类型的数目,只有当Ni、Nj满足一定条件时,两种类型的度分布情况才相互独立且无重叠.

图4 按照不同顶点类型统计的度分布(对应于图3(a)最小的峰值)
Fig.4 Degree distribution calculated for different types of vertexes(The figure corresponds to the lowest peak in Fig.3(a))
众所周知,随机网络的度分布为泊松分布,该结论有严格的证明[7,22]:

(3)
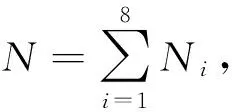

(4)
(5)
网络出现多个峰值时是p1较大、p2较小的情况.显然当p2足够小时,Q2与伯努利试验的二项分布概率解析形式相同,故Q2满足泊松分布的解析形式,即

(6)


(7)


(8)
由式(4)-(6)、(8)得到


(9)

若m∈M2,其度为k2,k2=k21+k22,同理可得到


(10)
同理可得到p(k3)、p(k4)、p(k5)、p(k6)、p(k7)和p(k8)的解析式,可写成普遍形式:


(11)
其中t=1,2,3,4,5,6,7,8,当t取不同的值时,表示不同顶点类型的概率解析式.
同理,若是p1较大、p2较小的情况,则Q1近似泊松分布,网络的度分布表达式可写为


(12)

3 网络节点的平均距离
网络节点的平均距离(
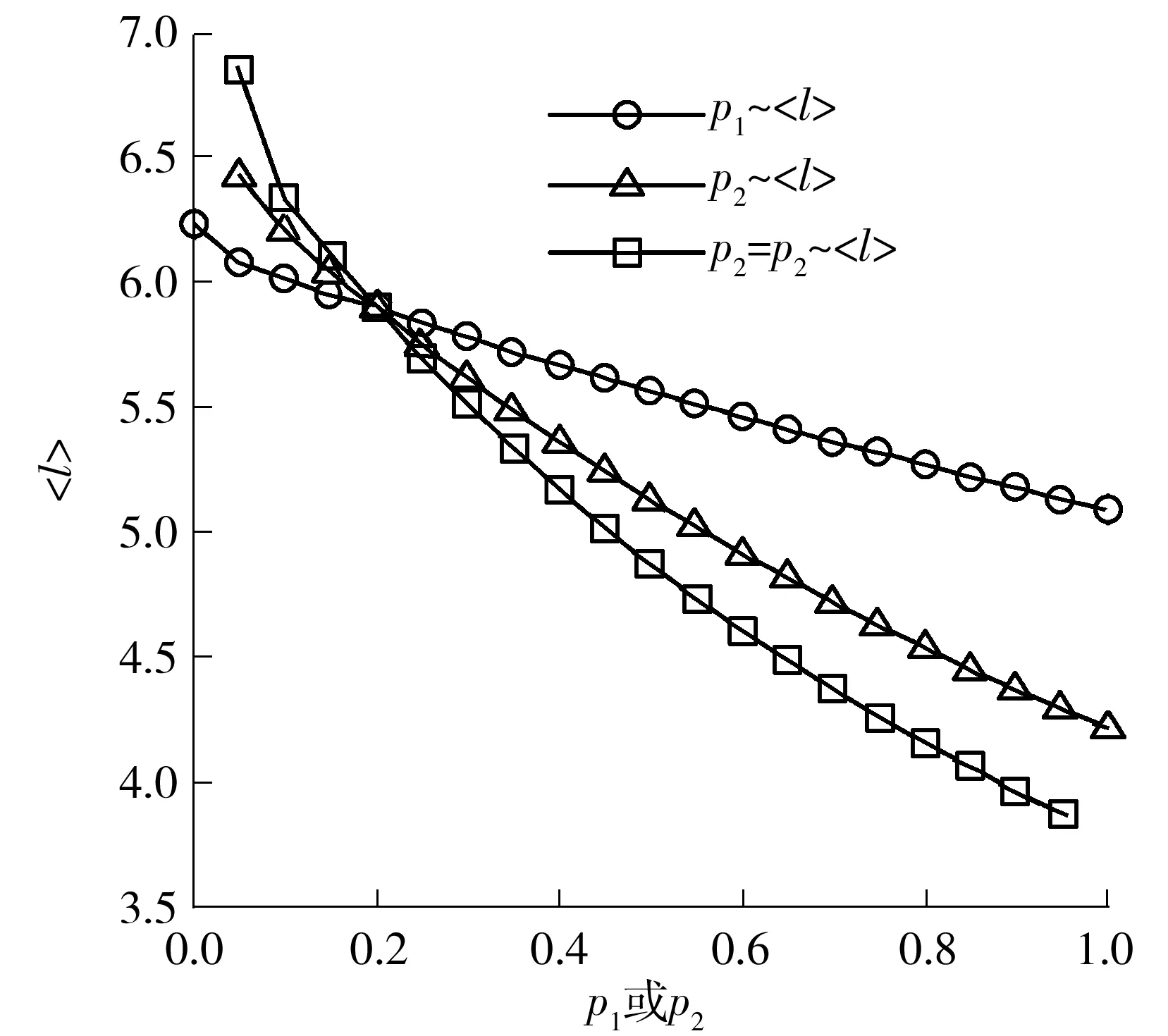
图5 网络平均距离与不同连接概率的关系
Fig.5 Average distance of the network versus the connecting probability
进一步研究平均距离与节点数目N的关系.图6是对同类型节点连接概率为p1=0.8、不同类型节点连接概率为p2=0.2时演化出的网络的计算结果.当N较小时,随着N的增加平均距离呈现减小的趋势;N在500~700左右时,随着N的增大,平均距离出现上下明显的波动;当N大于700时,随着N的增加,平均距离没有明显的变化,近似接近于一个常数,这个常数约为5.25.这是由于,当网络达到一定规模时,其边界效应的影响已不明显.
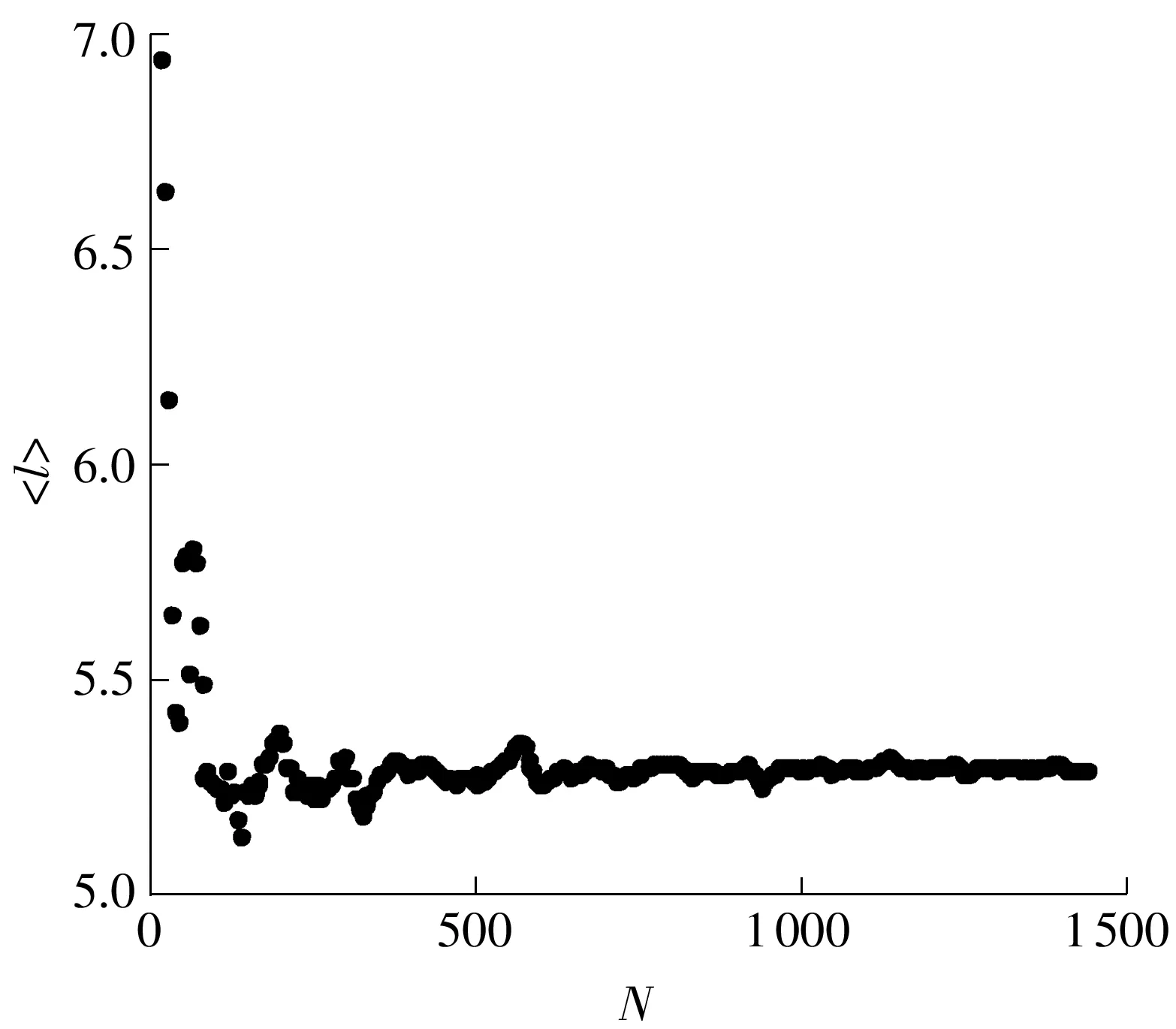
图6 网络的平均距离与网络节点数目的关系
Fig.6 Relationship between the average distance and the total node number of the network
4 网络的集群系数
复杂网络的集群系数是用来描述复杂网络中节点的邻点也互为邻点的比例情况,可用来衡量小集团结构的完美程度.文中关注的是集群系数与节点度的关系,该方面的研究显示,大多情况下满足幂函数关系[23- 26]:
C(k)∝k-α
(13)
α称为层次指数.普遍认为这个规律可说明网络存在“层次结构”,可理解为网络的节点聚合成许多小群体,而这些小群体又在某一个层次上聚合成较大的群体,形成一个个分层次的群体结构[2- 3,7].
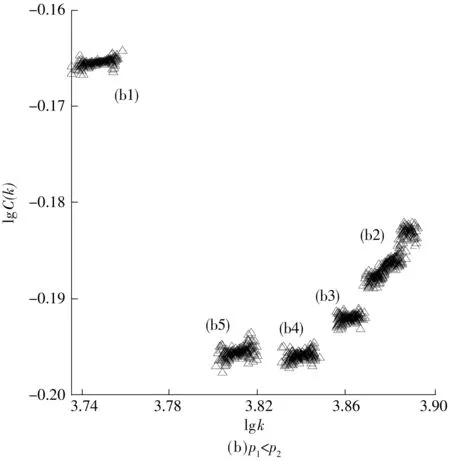
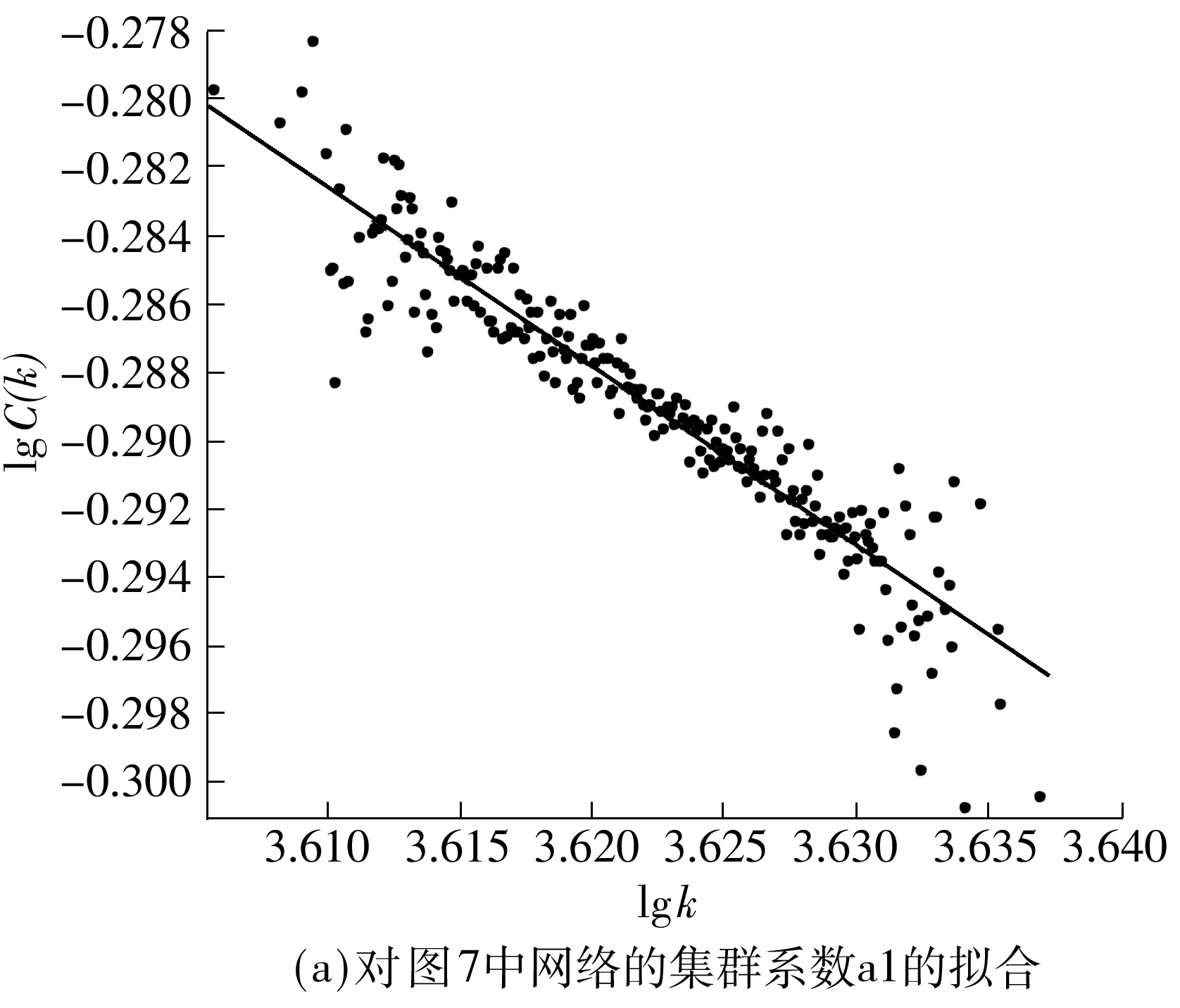
当p1>p2时,从整体上看,节点度大的平均集群系数也大,但是在某个局部来看,却正好相反,如图7(a)所示.而对于p1 图7 网络的集群系数与节点度的关系 Fig.7 Relationship between cluster coefficient and degree of nodes 根据以上结果可以看出,对于p1=0.8、p2=0.2演化出的网络,在不同的局部范围内,度值k越大则α越大,整体的α取值范围为0.020 8~0.515 7.而对于p1=0.2、p2=0.8演化出的网络,度值k越大则α越小,整体的α取值范围为-0.277 2~-0.029 1.后一种情况与这些实际网络的结果有着明显的区别. 文中从彭罗斯拼图出发,构造和研究了部分随机复杂网络模型的统计特征.首先按照彭罗斯拼图中顶点的8种类型,分别以不同的概率连接同类和异类顶点而构成网络.研究发现:其度分布为多个泊松分布或者近似泊松分布的叠加组合,其位置可通过调节两个连接概率的值而改变;节点间的平均距离随着节点总数N的增大出现一些波动,但当N足够大时,平均距离接近于常数5.25;网络的集群系数与节点度函数关系曲线为若干线段,满足C(k)∝k-α的幂函数关系,层次指数α的取值范围是不连续的,且有正值和负值.由此可知,作为二维准晶体模型的彭罗斯拼图亦可用于复杂网络的研究——一方面构造出新的网络模型,发现一些相应网络的特性,另一方面也可以通过复杂网络的特性来进一步认识准周期结构的性质. [1] ERDOS P,RÉNYI A.On the evolution of random graphs [J].Publication of the Mathematical Institute of the Hungarian Academy Sciences,1960,5(1):17- 60. [2] ERDOS P,RÉNYI A.On random graphs I [J].Publicationes Mathematicae-Debrecen,1959,6(1):290- 297. [3] WATTS D J,STROGATZ S H.Collective dynamics of small-world networks [J].Nature,1998,393(6684):440- 442. [4] BARRAT A,WEIGT M.On the properties of small-world networks models [J].European Physical Journal B,2000,13(3):547- 560. [7] ALBERT R,BARABSI A L.Statistical mechanics of complex networks [J].Reviews of Modern Physics,2002,74(1):47- 97. [8] FALOUTSOS M,FALOUTSOS P,FALOUTSOS C.On power-law relationships of the internet topology [J].ACM SIGCOMM Computer Communication Review,1999,29(4):251- 262. [9] EBEL H,MIELSCH L I,BORBHOLDT S.Scale-free topology of e-mail networks [J].Physical Review E,2002,66(3):035103- 035106. [10] SHECHTMAN D S,BLECH I,GRATIAS D.Metallic phase with long-range orientational order and no translational symmetry [J].Physical Review Letters,1984,53(20):1951- 1954. [11] BENDERSKY L.Quasicrystal with one-dimensional translational symmetry and a tenfold rotation axis [J].Physical Review Letters,1985,55(14):1461- 1463. [12] WANG N,CHEN H,KUO K H.Two-dimensional quasicrystal with eight-fold rotational symmetry [J].Physical Review Letters,1987,59(9):1010- 1013. [13] HE L X,LI X Z,ZHANG Z.One-dimensional quasicrystal in rapidly solidified alloys [J].Physical Review Letters,1988,61(9):1116- 1118. [14] YANG X B,LIU Y Y,FU X J.Transmission properties of light through the Fibonacci-class multilayers [J].Physical Review B,1999,59(7):4545- 4548. [15] ZENG X,UNGAR G,LIU Y.Supramolecular dendritic liquid quasicrystals [J].Nature,2004,428(6979):157- 160. [16] GUMMELT P.Penrose tilings as coverings of congruent decagons [J].Geometria Dedicata,1996,62(1):1- 17. [17] PENROSE R.The role of aesthetics in pure and applied mathematical research [J].The Institute of Mathematics and Its Applications Bulletin,1974,10(7):266- 271. [18] MACKAY A L.Crystallography and the Penrose pattern [J].Physica A:Statistical Mechanics and Its Applications,1982,144(1):609- 613. [19] 刘有延,傅秀军.准晶体 [M].上海:上海科技教育出版社,1999:3. [20] DE BRUIJN N G.Algebraic theory of Penrose’s non-perio-dic tilings of the planeⅠ&Ⅱ [J].Indagationes Mathe-maticae,1981,84(1):39- 66. [21] 傅秀军.准晶体覆盖模型的结构和电子性质 [D].广州:华南理工大学,2004. [22] 何大韧,刘宗华,汪秉宏.复杂系统与复杂网络 [M].北京:高等教育出版社,2009:126- 131. [23] XIAO W K,REN J,QI F.Empirical study on clique-degree distribution of networks [J].Physical Review E,2007,76(3):037102- 037105. [24] ALEXEI V,ROMUALDO P S,ALESSANDRO V.Large-scale topological and dynamical properties of the internet [J].Physical Review E,2002,65(6):066130- 066141. [25] BARABASI A L,OLTVAI Z N.Network biology:understanding the cell’s functional organization [J].Nature Reviews Genetics,2004,5(2):101- 113. [26] YOOK S H,OLTVAI Z N,BARABASI A L.Functional and topological characterization of protein interaction networks [J].Proteomics,2004,4(4):928- 942. Statistical Properties of Partially Random Complex Network Based on Penrose Tiling FU Xiu-jun PENG Cai-xia DUAN Xue-qing (School of Physics and Optoelectronics, South China University of Technology, Guangzhou 510640, Guangdong, China) In order to extend the models and exploit new features for complex networks,the statistical properties of random complex networks are explored.In the investigation,first,on the basis of the Penrose tiling composed of two kinds of rhombus,random connections of the vertex are added to construct a partially random complex network in which the connecting probability depends on the vertex type.Then,the main characteristic parameters of the network are calculated by using analytical and numerical methods.It is found that the degree distribution,the ave-rage inter-node distance and the cluster coefficient of the partially random complex network are all close to those of general random networks but obey different variation laws,which means that the proposed quasi-periodic complex network possesses not only the common properties of general networks but also abundant specific features. Penrose tiling; quasi-periodic structure; complex network; statistical property 2016- 01- 18 国家自然科学基金资助项目(11674102) Foundation item: Supported by the National Natural Science Foundation of China(11674102) 傅秀军(1964-),男,博士,教授,主要从事准晶体研究.E-mail:phxjfu@scut.edu.cn 1000- 565X(2017)06- 0001- 07 O 414.2 10.3969/j.issn.1000-565X.2017.06.001

5 结论
