基于正解过程的Risley棱镜光束指向控制精度分析
2017-08-01张鲁薇王卫兵王挺峰
张鲁薇, 王卫兵, 王 锐, 王挺峰, 郭 劲
(中国科学院 长春光学精密机械与物理研究所 激光与物质相互作用国家重点实验室,吉林 长春 130033)
基于正解过程的Risley棱镜光束指向控制精度分析
张鲁薇*, 王卫兵, 王 锐, 王挺峰, 郭 劲
(中国科学院 长春光学精密机械与物理研究所 激光与物质相互作用国家重点实验室,吉林 长春 130033)
为了获得Risley棱镜系统光束指向控制精度指标设计及性能提升的依据,对系统光束指向控制精度随轴系角度测量精度的非线性变化规律进行了研究。首先,以一级近轴近似矢量合成模型为基础,采用正解方法根据双棱镜方位推导了出射光束指向的解析表达式;然后,结合单自由度轴系伺服控制经验,通过泰勒级数展开的方式推导出了光束指向控制精度与轴系角度测量精度之间的非线性解析表达式,并由此获得了界定限判据;最后,分别对小偏向角系统和大偏向角系统进行了仿真分析,获得了光束指向控制精度在全视场区域内的变化情况。结果表明,本文研究所得的非线性解析式描述了影响系统光束指向控制精度诸多因素之间的相互关系,能够为Risley棱镜光束指向系统的设计及整体性能的优化提供依据。
光束指向;Risley棱镜;控制精度;正解;界定限
1 引 言
Risley棱镜由两个共轴相邻排列的棱镜组成,两个棱镜绕着共同轴独立旋转实现光束在锥角区域内的任意偏转[1]。相较于传统的两轴、三轴式光束转向机构,Risley棱镜具有结构紧凑、响应快、指向精度高、环境适应性好等优势,因而在激光通信、激光雷达、光学稳像、搜索与跟踪、激光三维成像等领域具有广阔的应用前景[2-5]。根据操作对象的不同,Risley棱镜的应用主要可以分为光束偏转和视轴偏转两大类[6]。美国已有多家研究机构研制出了用于机载激光通信、扫描与跟踪等应用的光束指向控制机构,国内国防科技大学研制出了同时具备光束扫描和步进成像两种工作模式的双旋转棱镜样机[7]。
目前,对于Risley棱镜系统的研究主要集中在光束指向机制、扫描模式、精密控制、成像特性、误差分析等方面。在光束指向机制方面,Jeon等人[8-14]对于如何获得正向问题与反向问题的近似解与精确解进行了探讨;在扫描模式方面,Gerald F等人[15-17]主要研究基于棱镜结构、旋转速度和棱镜初始位置等参数产生不同的扫描轨迹以及如何根据实际应用需求进行扫描模式的选择和优化;在精密控制方面,Sanchez M等人[18-20]主要研究伺服控制策略的设计及优化以实现棱镜的高效精密回转控制;在成像特性方面,LI A等人[21-23]对Risley棱镜引起的光束变形、像差等问题以及如何优化成像性能开展了研究;在误差分析方面,ZHAO Y等人[24-25]主要针对器件自身误差、棱镜方位误差、装调误差等误差源对光束指向精度的影响进行了相关分析。上述研究为Risley棱镜系统性能的提升及其应用领域的扩展提供了理论依据和方法引导。
光束指向控制精度是评价Risley棱镜系统性能的核心指标。然而,目前对于如何设计该指标以及如何综合多因素从整体上对该性能进行优化缺乏相关的理论依据。为了解Risley棱镜系统最终的光束指向控制精度和保精度控制的范围,本文针对光束指向控制精度与轴系角度测量精度之间的非线性关系展开了研究,目前这部分研究内容还未有文献涉及。
本文以一级近轴近似矢量合成正解分析为基础,结合轴系伺服控制经验,推导出了光束指向控制精度的非线性解析式及界定限判据,同时对小偏向角系统和大偏向角系统进行了仿真。
2 光束指向矢量合成理论
2.1 物理模型
根据棱镜对光束的偏转原理可知,单个棱镜旋转时将使光束沿等顶角圆锥面成圆周扫描。而当两块棱镜共轴相邻排列组成Risley棱镜时,通过两块棱镜独立旋转,可使光束在一定顶角的圆锥面内沿任意方向扫描。当满足一级近轴近似条件时,其扫描的圆锥面半顶角大小为两块单棱镜光束偏向角之和。
图1所示的三维空间Risley棱镜对光束的偏转对应的平面矢量投影如图2所示。Risley棱镜一级近轴近似矢量合成方法分析如下,其中,δ1代表棱镜1偏向角,δ2代表棱镜2偏向角,Φ和Θ分别代表δ1和δ2矢量合成后的偏转角和方位角。起始位置为θ1=0,θ2=0,此时Φ为最大值,方向为正δx。

图1 Risley棱镜光束偏转三维示意图Fig. 1 3D schematic diagram of beam steering for Risley prisms
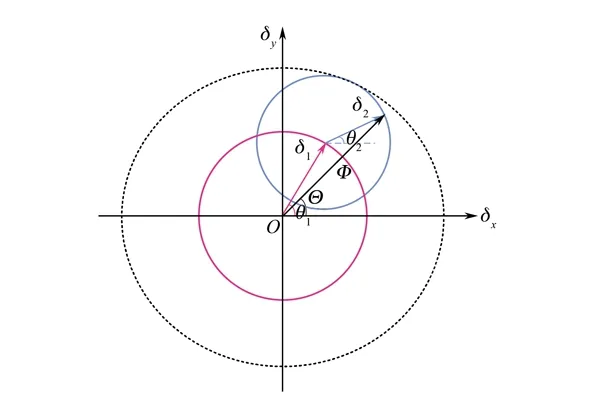
图2 Risley棱镜光束偏转平面矢量投影示意图Fig. 2 2D schematic diagram of beam steering for Risley prisms
2.2 一级近轴近似矢量合成正解分析
一级近轴近似是基于近轴条件下的薄棱镜近似。在该近似条件下,认为棱镜对光束的偏向角只与棱镜的顶角和折射率有关,因此棱镜1和棱镜2对光束的偏向角大小可分别表示为:
式中,A1、A2分别为棱镜1、棱镜2顶角,n1、n2分别为棱镜1、棱镜2折射率。
偏转角Φ矢量在坐标系Oδxδy下的分量为:
偏转角Φ和方位角Θ大小分别为:
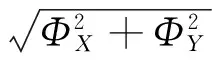
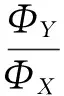
为了便于分析,进一步假设两块棱镜具有相同的顶角和材料,因此有:
|δ|=|δ1|=|δ2|=A(n-1).
由此可知其对应的偏转角Φ和方位角Θ仅与两块棱镜的旋转角度θ1,θ2有关,可分别简化为:

推导式(11)过程中,可以发现Risley棱镜系统全区域控制过程中存在奇异点,数学描述为:
结合实际考虑棱镜1和棱镜2独立可旋转的范围均为θ1,θ2∈[-π,π],则存在奇异点:
θ1-θ2=±π.
其对应的物理意义为当棱镜1和棱镜2斜面平行放置时,即光束经过Risley棱镜指向不偏转处为控制的奇异点,如图3所示。
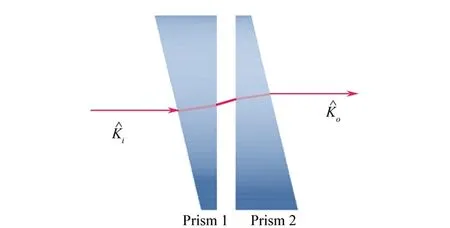
图3 奇异点:光束不偏转Fig. 3 No deflection of the incoming beam at the singularity
3 光束指向控制精度分析
3.1 单自由度轴系伺服控制精度分析
根据电机伺服控制系统工程经验可知,对于具体系统,通过闭环伺服控制算法设计可获得一定的闭环伺服控制系统带宽,进而可对一定的运动信号达到要求的保精度控制。Risley棱镜一般采用电机直驱传动形式来控制光束指向。轴系的闭环控制是决定Risley棱镜光束指向精度的重要因素。轴系的闭环控制精度一般与运动信号状态、系统装配误差、控制系统误差等因素相关,须结合实际系统进行具体分析。轴系闭环控制精度的理论极限为轴系角度测量精度,探讨轴系角度测量精度与光束指向控制精度的关系,具有更为普遍的研究价值。以此为依据,结合Risley棱镜工作特点,本文开展了轴系角度测量精度与光束指向控制精度关系的相关研究。
3.2 Risley棱镜光束指向控制精度分析
通过对式(10)、式(11)数学求导可间接获得Risley棱镜旋转过程中轴系角度测量精度对光束指向控制精度的影响。上面讨论已经对Risley棱镜做了简化约束,即认为δ只与棱镜顶角和折射率有关,而与入射角度和棱镜方位无关。因此光束指向控制精度只与棱镜1和棱镜2的旋转角度θ1和θ2有关。如果选择单一变量θ1或θ2进行研究,可分别获得其对光束指向控制精度的影响规律,但是需要采用分步遍历的方式进行分析,较为复杂,且独立分析θ1和θ2对光束指向控制精度的影响不利于整体规律的揭示。
考虑到上述原因,为同时获得棱镜1和棱镜2轴系角度测量精度Δθ1和Δθ2与光束偏转指向控制精度Δ|Φ|之间的关系,本文对|Φ|进行泰勒级数展开,如下所示:
由于轴系角度测量精度Δθ1和Δθ2为小量,因此可以忽略高阶项,从而得到:
Δ|Φ|=|Φ(θ1+Δθ1,θ2+Δθ2)|-
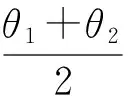
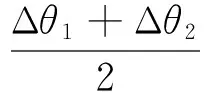
假设两棱镜完全相同,其旋转角度测量精度均为Δθ,因此可以得到如下不等式:
Δ|Θ|≤Δθ.
从式(18)可知偏转指向控制精度Δ|Φ|与Δθ的关系取决于棱镜1和棱镜2旋转角度偏差(θ1-θ2)和单个棱镜光束偏向角δ的大小。在不同区域偏转指向控制精度或低于或高于轴系角度测量精度,其界定限取决于:
护理结束后采取本院自制的满意度调查表对两组患者的满意度进行评价,以100分为满分,得分大于90分,评价为满意;得分在60~89分,评价为一般满意;得分小于59分,评价为不满意。
根据式(20)及式(10),可知界定限所对应的视场区域为圆,且在全视场范围内,在任一以视轴中心为圆心的圆周上每一点具有相同的光束指向控制精度。
从式(19)可知Risley棱镜光束方位指向控制精度Δ|Θ|与角度传感器测量精度Δθ相同,由于两者关系简单直观,因而在下文中不再对Δ|Θ|与Δθ关系展开详细讨论。
4 光束指向控制精度仿真分析
4.1 仿真计算
光束偏转指向控制精度与单棱镜对光束的偏向角有关,因此分为小偏向角系统和大偏向角系统两种情况进行讨论分析。大偏向角系统不满足近轴近似条件,与小偏向角系统相比,采用上述方法计算光束指向控制精度会存在一定的偏差,但不影响大偏向角系统光束指向控制精度整体规律的描述。
4.1.1 小偏向角系统
设定棱镜顶角15°,材料为k9(在550 nm处折射率为1.518 10),根据式(9)计算可得|δ|=0.136 rad。
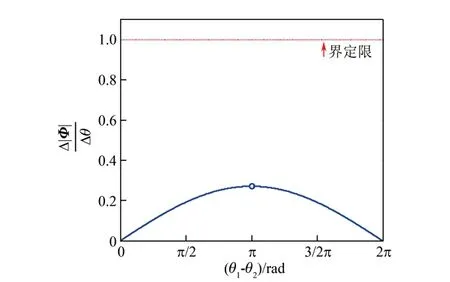
图4 小偏向角系统随(θ1-θ2)变化曲线Fig. 4 Curve of with (θ1-θ2) in small deflection angle system
4.1.2 大偏向角系统
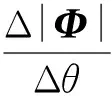

图5 大偏向角系统随(θ1-θ2)变化曲线Fig. 5 Curve of with (θ1-θ2) in large deflection angle system
根据图5中实际变化曲线与界定限的交点,通过计算可获得Risley棱镜系统工作过程中光束偏转指向控制精度或低于或高于轴系角度测量精度的相应视场区域。由于该曲线关于θ1-θ2=π对称,而θ1-θ2=a与θ1-θ2=2π-a实际对应的视场区域一致,因而只对图5中的(θ1-θ2)∈[0,π)部分展开讨论。
根据式(20)和式(10),求得界定限对应θ1-θ2=1.367 rad,界定限处光束指向偏转角为|Φ|=1.228 rad。
根据上述计算结果,绘制图6,从图中可以看到视轴中心为奇异点,圆锥半角为1.228 rad区域内光束偏转指向控制精度低于轴系角度测量精度。而在圆锥半角为1.228 rad至1.584 rad范围内所对应的视场区域光束偏转指向控制精度高于轴系角度测量精度。
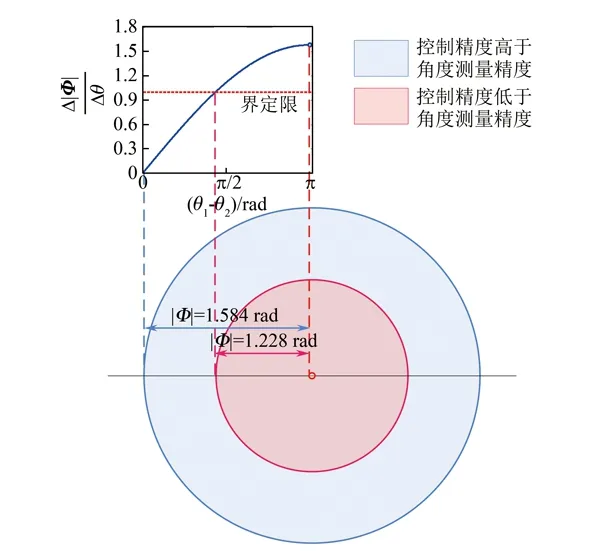
图6 界定限所对应的视场区域Fig. 6 Field of view corresponding to the dividing line
4.2 分析讨论
从上述仿真计算结果可以看出,不同的Risley棱镜光束指向系统具有不同的光束指向控制精度。小偏向角系统的光束指向控制精度整体上优于大偏向角系统。式(18)实际是一个对系统光束指向控制精度有影响的诸多因素相互关联的关系式,包括折射率、棱镜顶角、轴系角度测量精度等。通过式(18)和式(19),可以获得全视场区域内光束指向控制精度,为Risley棱镜光束指向系统设计时的性能指标提供参考。此外,可以获得光束指向控制精度在整个视场区域内的非线性变化情况以及相关影响因素,以此为依据对系统进行设计和优化。
本文所讨论的光束指向控制精度为理论极限,在实际工程应用中,可以针对具体系统的特性,设定合理的系数,获得适用于实际系统的光束指向控制精度,也可以根据实际系统性能要求设计界定限判据来获得相应的保精度控制范围。
5 结 论
本文针对Risley棱镜光束指向系统的非线性工作特点,基于一级近轴近似矢量合成模型及正解分析方法,并结合伺服控制系统经验,通过进一步数学处理,获得了光束指向控制精度与轴系角度测量精度之间的非线性解析表达式。此外,针对小偏向角系统和大偏向角系统分别进行了仿真计算分析。本文研究结果为Risley棱镜光束指向控制精度指标的设计提供了理论依据,也为光束指向系统的设计和优化提供了指导,具有一定的工程实用价值。
[1] MARSHALL G F,STUTZ G E.HandbookofOpticalandLaserScanning[M]. Boca Raton:CRC Press,2011.
[2] SCHWARZE C R,VAILLANCOURT R,CARLSON D,etal.. Risley- prism based compact laser beam steering for IRCM,laser communications,and laser radar[EB/OL]. [2016-11-16]. http://www.optra.com/images/TP-Compact-Beam-Steering.pdf
[3] SCHUNDLER E,CARLSON D,VAILLANCOURT R,etal.. Compact,wide field DRS explosive detector[C].Chemical,Biological,Radiological,Nuclear,andExplosives(CBRNE)SensingXII,IEEE,Orlando,USA,April 25,2011:80181O.
[4] DIXON J,ENGEL J R,SCHWARZE C. Risley prism universal pointing system (RPUPS)[J].SPIE,2015,9579:95790B.
[5] SCHWARZE C. A new look at Risley prisms[J].PhotonicsSpectra,2006,40(6):67-70.
[6] 范大鹏,周远,鲁亚飞,等. 旋转双棱镜光束指向控制技术综述[J]. 中国光学,2013,6(2):136-150. FAN D P,ZHOU Y,LU Y F,etal.. Overview of beam steering technology based on rotational double prisms[J].ChineseOptics,2013,6(2):136-150. (in Chinese)
[7] 洪华杰,周远,陶忠,等. Risley棱镜在光学侦察中的应用[J]. 应用光学,2014,35(2):179-187. HONG H J,ZHOU Y,TAO ZH,etal.. Application of risley prism on optical reconnaissance[J].JournalofAppliedOptics,2014,35(2):179-187. (in Chinese)
[8] JEON Y G. Generalization of the first-order formula for analysis of scan patterns of Risley prisms[J].OpticalEng.,2011,50(11):113002.
[9] 周远,鲁亚飞,黑沫,等. 旋转双棱镜光束指向解析解[J]. 光学 精密工程,2013,21(6):1373-1379. ZHOU Y,LU Y F,HEI M,etal.. Analytic solution of optical beam steering based on rotational double prisms[J].Opt.PrecisionEng.,2013,21(6):1373-1379. (in Chinese)
[10] 周远,鲁亚飞,黑沫,等. 旋转双棱镜光束指向的反向解析解[J]. 光学 精密工程,2013,21(7):1693-1700.
ZHOU Y,LUY F,HEI M,etal.. Analytical inverse solutions for rotational double prism beam steering[J].Opt.PrecisionEng.,2013,21(7):1693-1700. (in Chinese)
[11] LI Y. Third-order theory of the Risley-prism-based beam steering system[J].Appl.Opt.,2011,50(5):679-686.
[12] LI J. High precision pointing system based on Risley prism: analysis and simulation[J].SPIE,2015,9255:92551I
[13] LI A,SUN W,YI W. An overview of inverse solution expressions for Risley-prism-based scanner[J].SPIE,2016,9947:99470Z.
[14] LI A H,LIU X SH,SUN W S. Forward and inverse solutions for three-element Risley prism beam scanners[J].Opt.Express,2017,25(7):7677-7688.
[15] GERALD F,MARSHALL. Risley prism scan patterns[J].SPIE,1999,3787:74-86.
[16] SCHITEA A,DUMA V F. Modeling of Risley prisms devices for exact scan patterns[J].SPIE,2013,8789:878912.
[17] LU Y F,ZHOU Y,HEI M,etal.. Frame frequency prediction for Risley-prism-based imaging laser radar[J].Appl.Opt.,2014,53(16):3556-3564.
[18] SANCHEZ M,GUTOW D. Control laws for a three-element Risley prism optical beam pointer[J].SPIE,2006,6304:630403.
[19] GARCIA-TORALES G,FLORES J L,MUNOZ R X. High precision prism scanning system[J].SPIE,2007,6422:64220X.
[20] LU W,LIU L R,SUN J F. Control loop analysis of the complex axis in satellite laser communications[J].SPIE,2010,7814:781410.
[21] LI A,ZUO Q,SUN W,etal.. Beam distortion of rotation double prisms with an arbitrary incident angle[J].Appl.Opt.,2016,55(19):5164-5171.
[22] SANGHERA J S. Broadband beam steering using chalcogenide-based Risley prisms[J].OpticalEng.,2011,50(50):103-108.
[23] WEBER D C,TROLINGER J D,NICHOLS R G,etal.. Diffractively corrected Risley prism for infrared imaging[J].SPIE,2000,4025:79-86.
[24] ZHAO Y,YUAN Y. First-order approximation error analysis of Risley-prism-based beam directing system[J].Appl.Opt.,2014,53(34):8020-8031.
[25] ZHANG H,YUAN Y,SU L,etal.. Beam steering uncertainty analysis for Risley prisms based on Monte Carlo simulation[J].Opt.Eng.,2017,56(1):014105.
Analysis of beam steering control precision for Risley prismsbased on forward solution
ZHANG Lu-wei*, WANG Wei-bing, WANG Rui, WANG Ting-feng, GUO Jin
(State Key Laboratory of Laser Interaction with Matter,Changchun Institute of Optics,Fine Mechanicsand Physics,Chinese Academy of Sciences,Changchun 130033,China)*Corresponding author, E-mail:zhanglw@ciomp.ac.cn
In order to obtain the basis for index design of beam steering control precision and performance improvement for Risley prism system, the nonlinear relationship between Risley prism beam steering control precision and shaft angle measurement precision is investigated. First, based on the first-order paraxial approximation vector synthesis model, the analytical expression of the direction of the outgoing beam is derived from the double prisms position by the forward solution method. And then, based on the servocontrol experience of single degree of freedom shaft, the nonlinear analytical expression between the beam steering control precision and the shaft angle measurement precision is deduced by the Taylor series expansion method, and thus the dividing line criterion is obtained. Finally, the small deflection angle system and the large deflection angle system are simulated and analyzed respectively, and the change of the beam steering control precision over the whole field of view is obtained. Results show that the nonlinear analytical expression derived in this paper represents the relationship among the factors that affect the control precision of the system, which provides the basis for the design and optimization of the Risley prism beam steering system.
beam steering;Risley prism;control precision;forward solution;dividing line
2017-05-12;
2017-06-09
中国科学院国防科技创新基金项目(No.CXJJ-17-M132) Supported by National Defense Science and Technology Innovation Fund of Chinese Academy of Sciences (No. CXJJ-17-M132)
2095-1531(2017)04-0507-07
O439;TH703
A
10.3788/CO.20171004. 0507

张鲁薇(1988—),女,浙江杭州人,硕士,研究实习员,2014年于浙江大学获得硕士学位,主要从事激光应用技术方面的研究。E-mail: zhanglw@ciomp.ac.cn
