普采工作面正悬臂梁与倒悬臂梁支护梁的挠度研究
2017-07-31林智馨程虹铭
林智馨,程虹铭
(山西大同大学煤炭工程学院,山西大同037003)
普采工作面正悬臂梁与倒悬臂梁支护梁的挠度研究
林智馨,程虹铭
(山西大同大学煤炭工程学院,山西大同037003)
在普采工作面,按铰接顶梁与液压支柱的配合关系,可分为正悬臂梁与倒悬臂梁。为了分析正悬臂梁与倒悬臂梁在支护中顶板对梁破坏程度,运用龙格-库塔法,对同一均匀截面的梁在不同荷载作用下的挠度实验分析研究,得出梁上不同点的挠度,从中可以得出:正悬臂梁支护方式中顶板对梁的损害程度比倒悬臂梁支护方式中要小;且同一荷载作用下,离自由端越近梁的变形程度越大。这些结论可以为普采工作面中铰接顶梁与液压支柱的配合提供理论根据,以减少对顶梁破坏,保证顶板的稳定性,实现矿井的连续生产。
普采工作面;正悬臂梁与倒悬臂梁;铰接顶梁;四阶龙格-库塔法
随着矿井开采深度的加深,工作面顶板的压力越来越大,导致矿井灾害不断发生,造成大量人员伤亡,给煤矿生产带来了巨大经济损失。为了保证工作面顶板的稳定,保证矿井能正常生产,有必要对采煤工作面采用何种支护方式以及支护方式的稳定性进行实验分析研究。
以普采工作面为例,其支护方式为铰接顶梁配合单体液压支架,铰接顶梁和单体液压支架布置与煤层赋存条件,顶底板性质相适应,并符合采煤机割煤特点[1]。除确保回采空间作业安全外,还要力求减少支设工作量和对设备的损害。支护中铰接顶梁和液压支架的配合可分为正悬臂梁和倒悬臂梁,正悬臂梁支架悬臂的长段在立柱的煤壁侧,来自顶板的荷载被煤壁分担一部分,有利于支护机道上方顶板,顶梁不易折损;而倒悬臂梁支架则相反,由于其长段伸向采空区,顶板的荷载没有煤壁为其分担,梁的长段易损坏[2]。
本文根据悬臂梁的模型,提出梁的挠度(构件在荷载作用下竖直方向的变形)方程,并采用四阶龙格-库塔法,根据实验数据的不同对正悬臂梁与倒悬臂梁顶板对梁的损害程度做出预测,为普采工作面易采用何种支护方式提供依据。
1 问题分析及模型
普采工作面采用正悬臂梁支护的时候,顶板的荷载一部分被煤壁所承受;而在倒悬臂梁支护方式中,顶梁伸向采空区,顶梁承受顶板的全部荷载,造成梁的破坏程度不同。假设顶梁是均匀横截面梁,顶梁可以看做一端固定,一端自由的悬臂梁模型[3]。

图1 均匀横截面悬臂梁受力示意图
均匀横截面梁受力情况,见图1,其关于挠度y的微分方程为:

悬臂梁的挠度为二阶微分方程,其初始条件可以确定,该问题可转化为一阶方程组的初值问题,可运用四阶龙格-库塔法求解[4]。
2 四阶龙格-库塔格式解二阶方程的原理
对于二阶方程的初值问题[5],有:

引进新的变量z=y',即可化为下列一阶方程组的初值问题:

针对这个问题应用四阶龙格-库塔格式,有:

根据四阶龙格-库塔格式对方程组的展开形式有:

如果消去K1,K2,K,3K4,则上述格式可表示为:

这里,

3 算法的Matlab实现
3.1 实验数据
根据实际情况以及问题模型,本实验数据L取固定长度1 m,正悬臂梁的荷载pl2/EI=0.2,倒悬臂梁的荷载pl2/EI=0.5。
由挠度y的微分方程可得:
对正悬臂梁,有

对倒悬臂梁,有
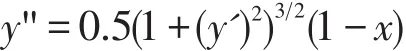
设初始条件y(0)=0,y'(0)=0,取步长h=0.2,处理数据可得以下两个微分方程组:

3.2 Matlab程序代码
3.2.1 建立方程组(1)的M文件[6]

其实现的MATLAB代码如下:

3.2.2 建立方程组(2)的M文件


其实现的MATLAB代码如下:

4 计算结果及分析
方程组(1)和(2)的MATLAB输出结果,见表1。

表1 结果分析
由表1可知,荷载的大小对梁的挠度影响是比较大的。
(1)在同一点处,倒悬臂梁顶梁的挠度大于正悬臂梁顶梁的挠度,且随着长度的增加,现象更明显。
(2)在同一荷载作用下,同一顶梁上随着测点距自由端距离的减小,挠度值将逐渐增大。
5 结论
运用四阶龙格-库塔法,对不同载荷下正悬臂梁与倒悬臂梁顶梁的挠度进行分析得出:
(1)在相同的载荷和节点上,正悬臂梁顶梁的挠度比倒悬臂梁顶梁的挠度要小,即变形量小。说明在同一工作面顶板对正悬臂梁的顶梁损害变形程度比倒悬臂梁的要小。
(2)随着工作面向前推进,老顶初次来压步距较大,工作面来压显现越剧烈相应的动压系数也越大,为了保证工作面设备及人员的安全,宜采用正悬臂梁支护方式,且悬臂支护的距离不宜过大。
(3)当工作面出现周期来压时,顶板下沉速度急剧增加,顶板下沉量变大,顶梁所受的载荷普遍增加,如果所选择的支护方式不合适可能导致煤壁片帮,顶梁折损,顶板发生台阶下沉,为此应选用正悬臂梁支护方式支护。
[1]徐永圻.煤矿开采学[M].徐州:中国矿业大学出版社,1999.
[2]钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.
[3]徐杏华,肖孟,李朝.平面杆系结构稳定问题的常微分方程解法[J].三峡大学学报,2011,33(1):63-72.
[4]杨泮池,乔学军,林芳,等.计算方法[M].西安:西安交通大学出版社,2005.
[5]李庆杨,王能超,易大义.数值分析[M].武汉:华中科技大学出版社,2010.
[6]张德丰.MATLAB数值分析[M].北京:机械工业出版社,2012.
Beam Deflection Research of Positive Cantilever Beam and Invertecl Cantilever Beam in General Mining Working Face
LIN Zhi-xin,CHENG Hong-ming
(School of Coal Engineering,Shanxi Datong University,Datong Shanxi,037003)
In the general mining working face,according to the hinged top beam and pillar of the relation,there are positive canti⁃lever beam and cantilever beam.Now in order to analyse the damage cantilever beam and cantilever beam in support of roof beam dam⁃age,by using the Runge-Kutta method,the same uniform cross section beam under different loads were analysed and researched,ob⁃taining the beam deflection of different points,analyse the damage cantilever beam supporting method caused less beam damage than inverted cantilever support;and under the same loads the mearer from the free end,thebigger the cleflection.These conclusions can be used as ordinary mining face with hydraulic prop in hinged cooperation and provide a theoretical basis to reduce the beam damage,en⁃sure the stability of the roof,to realize the continuous production of mining.
general mining working face;positive cantilever beam and cantilever beam;hinged top beam;four order Runge-Kut⁃ta method
TD355
A
1674-0874(2017)03-0064-03
〔责任编辑 王东〕
2016-06-20
林智馨(1964-),女,山西大同人,实验师,研究方向:计算机应用。
