关于几类拓扑空间序列的收敛性
2017-07-31张芳
张 芳
(山西大同大学数学与计算机科学学院,山西大同037009)
关于几类拓扑空间序列的收敛性
张 芳
(山西大同大学数学与计算机科学学院,山西大同037009)
拓扑空间序列的收敛性是拓扑学的一个重要内容,通过拓扑空间序列收敛的定义,对于几类常用的拓扑空间,给出序列收敛的有关性质。
拓扑空间;序列;收敛性
在数学分析课程中,已经证明了一个序列如果收敛则极限唯一,因此可以从序列收敛的概念出发来研究集合的凝聚点、函数在某一点处的连续性,但在一般的拓扑空间中情况未必如此。本文主要研究几种常用类型拓扑空间序列的收敛性,为了讨论方便首先给出以下几个定义:
定义1设X是一个拓扑空间,每一个映射S:Z+→X叫做X中的一个序列。我们常将序列S记作或者或者记作
定义2设是拓扑空间X中的一个序列,x∈X。如果对于x的每一个邻域U,存在M∈Z+使得当i>M时,有xi∈U,则称点x是序列的一个极限点(或极限),也称为序列收敛于x。记作
如果序列至少有一个极限,则称这个序列是一个收敛序列。如果序列没有极限,则称这个序列是一个发散序列。
注通过定义2可知拓扑空间中序列的收敛性与它所在的拓扑有关。
定理1平庸空间中任何一个序列都收敛,并且收敛于它中的每一点。
证明设X是一个平庸空间,是X中一个序列。任取x∈X,由于点x的邻域只有X,故对于任意的i∈Z+,xi∈X。于是由定义2可知,序列收敛于x,即
说明1若平庸空间X中至少含有两个点,则X中的序列收敛点不唯一。
定理2设是离散空间X中的一个序列,则序列收敛当且仅当存在M∈Z+使得当时有 xi=xj。
证明必要性。设序列收敛于x∈X。由于X为一个离散空间,所以X中的每一个单点集都是开集,于是{}x为点x的一个邻域,根据定义2可知存在 M∈Z+使得当i,j>M 时,有 xi,xj∈{}x,从而xi=x=xj。[4]
充分性。若存在 M∈Z+使得当i,j>M时有xi=xj。不妨设x=xi=xj,则x∈X。于是对于x的每一个邻域U,存在 M∈Z+使得当i>M 时,有xi=x∈U。因此由定义2可知,
定理3设X是一个含有不可数多个点的可数补空间,则X中一个序列收敛于x∈X的充分必要条件是存在M∈Z+使得当i>M时,有xi=x。
证明充分性由定义2显然成立。下面证明必要性。设,由于集合是一个可数集,因此D的补集D′是x的一个邻域,于是存在 M∈Z+,使得当 i>M 时有 xi∈D′,此时有xi=x。
说明2当X是一个含有可数多个点的可数补空间,则X成为一个离散空间,从而X中序列的收敛性由定理2可得。
定理4设X是一个含有无限多个点的有限补空间,是X中的任何一个由两两互不相同的点构成的序列,即当i≠j时,有 xi≠xj,则序列{xi}i∈Z+收敛并且X中的每一点都是它的收敛点。
证明设{xi}i∈Z是X中满足条件的序列。任取x∈X,U为x的任意一个邻域,由于拓扑空间X为有限补空间,故U的补集U′是一个有限集,所以序列中最多只有有限个元素在U的补集U′中,于是存在 M∈Z+使得当 i>M 时有 xi∈U。即因此序列收敛于X中的任何一个点。
说明3若X为含有有限多个点的有限补空间,则X为一个离散空间,从而X中序列的收敛性由定理2可得。
定理5设X是一个度量空间,则X中的任何一个收敛序列都只有唯一的极限。
证明设X是一个度量空间,ρ为X的度量,是X中一个收敛序列。
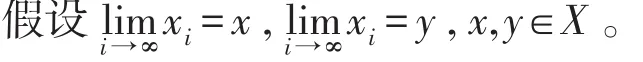

说明4由于实数空间ℜ和n维欧式空间ℜn都是度量空间,所以数学分析所研究的收敛序列都只有唯一极限。
[1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010.
[2]熊金城.点集拓扑讲义[M].北京:高等教育出版社,2011:90-94.
[3]方嘉琳.点集拓扑学[M].辽宁:辽宁人民出版社,1987.
[4]张芳.关于度量空间的几个性质[J].山西大同大学学报(自然科学版),2008,24(6):5-9.
Sequential Convergence for Several Types of Topological Spaces
ZHANG Fang
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)
The sequential convergence is an important content about topological space.In this paper,by using the definition of se⁃quential convergence and under several category type of topological spaces,we present the relevant properties of sequential conver⁃gence.
topological space;sequence;convergence
O189.11
A
1674-0874(2017)03-0020-02
〔责任编辑 高海〕
2017-03-20
张芳(1968-),女,山西阳高人,硕士,讲师,研究方向:拓扑学与非线性泛函分析。
