运城市参考作物需水量预测研究

郭志忠

（山西省汾河灌溉管理局一坝管理站）

运城市参考作物需水量预测研究

郭志忠

（山西省汾河灌溉管理局一坝管理站）

作物需水量一般可以采用参考作物需水量法来进行估算。以运城市为例，根据多年参考作物需水量（ET0）历史资料，在对其动态变化特征分析的基础上，分别构建了两种不依赖于气象资料的简单季节模型和SIN-ET0经验模型。对模型进行率定和验证结果表明：平均相对误差10.73%和11.13%，具有较为满意的预测效果，可为当地的参考作物需水量估算提供有效方法。

参考作物需水量 简单季节模型 SIN-ET0模型 预测 运城市

作物需水量的定义具有多种表述方式，但都可归结为有效耗水和无效耗水之和。参考作物系数法是计算作物需水量（ET0）最常见的方法之一，该方法的关键在于如何确定ET0和作物系数。作物系数通常可以采用联合国粮农组织的推荐值；ET0采用计算获取，一般采用Penman-Monteit公式法、人工智能方法和Hargreaves公式法等，但这些方法需要详尽的气象资料才能够予以应用。本项研究以运城市为例，结合当地参考作物需水量历史资料，在对数据动态特征分析的基础上，建立合理可行的ET0预测模型，旨在为ET0的估算提供一种有效方法。

1 市域简况

运城市位于山西省最南部，与临汾市和晋城市毗邻，与河南省和陕西省隔黄河相望。受季风活动影响，属暖温带大陆性气候，年均气温13.3℃。多年平均降水量525 mm，冬春稀少，夏秋集中。运城市属中华农耕文明的发源地，气候条件适宜种植农作物，农业生产历史悠久，长期以来一直是全省最为主要的粮棉产区。

2 时间序列模型介绍

时间序列是一种基于数理统计学的数据深度挖掘方法，旨在于深入揭示随机时间序列的统计学规律。通常，在时间序列模拟研究中，指数平滑模型的使用最为常见。某一期的指数平滑值计算原理为：将前一期的指数平滑值与该期的样本观测值加权平均，并对权值进行合理修正，从而可避免摇摆效应的影响，最终获得较为理想和较为平滑的时间序列。通常根据该时间序列是否具有季节性效应，从而将模型划分为非季节性和季节性两大类，两大类模型还能下分许多小类，各种模型的特点及适用条件如表1所示。

表1 指数平滑模型分类及其适用条件

3 数据来源及处理

本研究选取了1957-2012年运城市逐月的参考作物需水量资料，数据主要来源于国家农业科学数据共享中心。首先，通过对数据变化趋势和季节性趋势的分析，并结合常见时间序列模型的特点，大致确定模型的基本类型；然后，分别采用80%和20%的数据样本对模型进行率定和验证。其中，率定样本为1957年1月至2001年10月的数据资料，共538组；验证样本为2001年11月至2012年12月的数据资料，共134组。时间序列模拟和数据非线性拟合分别采用SPSS 19软件和Matlab 2013b进行。主要采用两种统计学指标（均方根误差和平均相对误差）对模型的预测效果进行评价，计算公式如下：

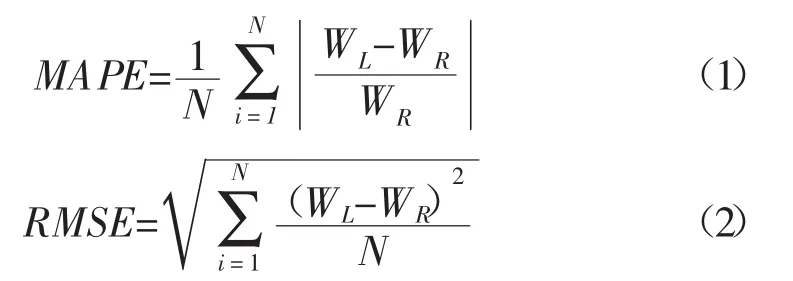
式中：WL为参考作物需水量预测值，mm；WR为参考作物需水量实测值，mm。

4 结果与分析

4.1 参考作物需水量动态变化特征分析

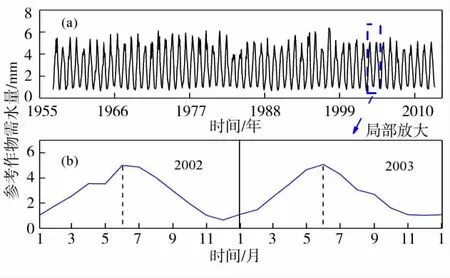
图1 参考作物需水量动态变化过程

图1为1957-2012年运城市参考作物需水量（ET0）动态变化过程。由图1（a）可知，该区域参考作物需水量随时间呈现锯齿状的波动趋势，波动范围介于0.63-6.37 mm之间，参考作物需水量的多年均值为2.79 mm。由图1（a）还可以看出，参考作物需水量在固定区间内呈现往复波动，但整体上并无单调递增或衰减的变化趋势。由于参考作物需水量变化存在一定的周期性特征，因此只选取2002年与2003年为代表，对作物需水量的年内变化特征进行分析。由图1（b）可以看出，参考作物需水量随时间呈现先逐渐增大然后逐渐减小的变化趋势，并且每年都在6月左右出现极大值。综上来看，ET0并没有明显的趋势性，并且季节性影响能够随时间变动而保持恒定，说明运城市的ET0动态变化过程能够采用简单季节模型来进行描述。此外，由图1还可以看出，该动态变化过程近似于周期性的正弦函数。因此，ET0还可以采用周期性的正弦经验模型进行描述。

4.2 参考作物需水量模拟研究

由于研究区域参考作物需水量的无趋势性和季节性，本文采用简单季节模型对其动态变化过程进行描述。简单季节模型的精度好坏，主要取决于水平参数和季节参数的取值是否合理。首先，采用80%数据样本对该模型的参数进行率定，结果表明水平参数为0.099，季节参数为4.731E-6；然后，从模型预测值和实测值的线性一致性、MAPE值和RMSE值三个方面对模型的率定效果进行合理评价。图2为简单季节模型预测值和实测值间的线性关系。由图2可知，对于率定组样本，两者所构成的线性拟合模型的斜率为0.90，说明两者之间具有较好的一致性。经计算，它们两者间的平均相对误差和均方根误差分别为12.85%和0.44，说明简单季节模型的率定效果基本满意，可用于当地参考作物蒸发蒸腾量的预测。将134组验证集样本带入训练好的简单季节模型，便可得到验证集的预测值。由图2可以看出，对于验证组样本，两者所构成的线性拟合模型的斜率为1.02。验证集样本预测值与实测值的MAPE和RMSE分别为10.73%和0.35。说明采用简单季节模型进行ET0的预测可以取得较为满意的效果。

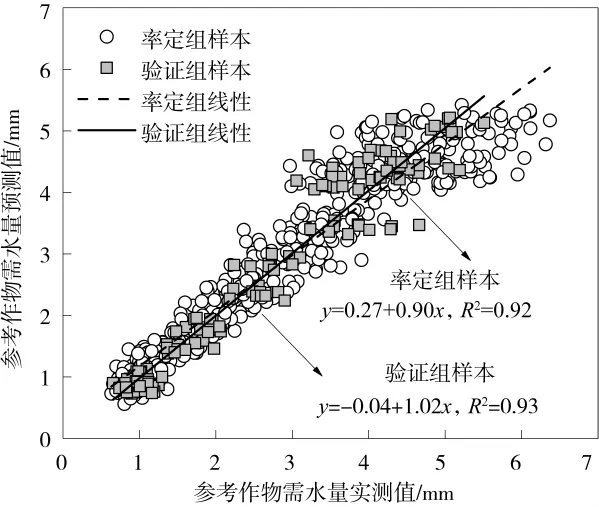
图2 简单季节模型预测值与实测值间的线性关系

同时，还研究构建了ET0计算经验模型，如式（3）所示。

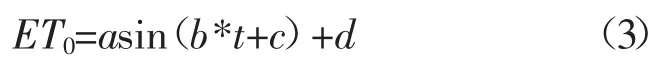
式中：ET0为参考作物需水量，mm；a、b、c和d均为模型系数。

同样选取1957年1月至2001年10月的数据资料对参数进行优化率定，结果如表2所示。图3为SINET0经验模型的预测值与实测值间的线性关系。对于率定组样本，两者所构成的线性拟合模型的斜率为0.89，说明两者具有较好的一致性。经计算，率定组样本实测值与预测值间的平均相对误差和均方根误差分别为13.4%和0.47，说明模型率定基本符合精度要求。对于验证组样本，预测值与实测值之间具有较好的一致性（线性方程斜率为1.00）和较小的误差（MAPE=11.13%，RMSE=0.38），说明该模型取得了较为满意的预测效果。

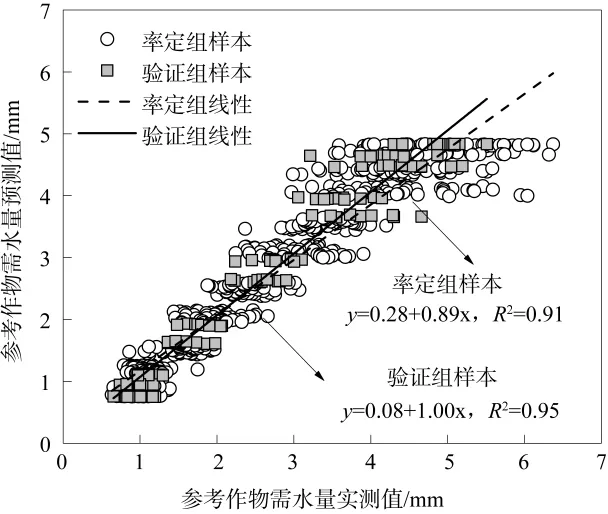
图3 SIN-ET0经验模型预测值与实测值间的线性关系

表2 SIN-ET0经验模型参数

将简单季节模型与SIN-ET0模型进行对比分析，可知简单季节模型的误差更小，预测精度更高，但优势并不是非常明显。比较图2和图3可以发现，在较高参考作物需水量范围时（ET0＞5），两种模型的预测效果均较差，预测结果偏小。由此也可以说明，这两种模型的适用范围为0 mm＜ET0＜5 mm。对于两种模型存在的缺陷，是下一步有待深入研究的方向之一。

5 结论

（1）运城市的参考作物需水量在年际间呈现锯齿状的波动趋势，在年内呈现先逐渐增大然后逐渐减小的变化趋势。

（2）运城市的参考作物需水量可采用简单季节模型进行描述，该模型的平均相对误差为10.73%，预测效果较为满意。

（3）SIN-ET0模型的平均相对误差为11.13%，预测精度较好，也可用于运城市参考作物需水量的预测。

（4）相对SIN-ET0模型，简单季节模型的预测效果略优。两种模型的适用范围为0 mm＜ET0＜5 mm。

[1]陈玉民.中国主要作物需水量与灌溉[M].北京：水利电力出版社，1995.

[2]ALIENRG，PEREIRALS，RAESD,et al.Crop evapotranspiration guidelines for computing crop water requirements.FAO irrigation and drainage paper 56[M].Rome,Italy：FAO，1998.

[3]徐俊增，彭世彰，张瑞美，等.基于气象预报的参考作物蒸发蒸腾量的神经网络预测模型 [J].水利学报，2006（3）：376-379.

[4]赵 永，蔡焕杰，王 健，等.Hargreaves计算参考作物蒸发蒸腾量公式经验系数的确定[J].干旱地区农业研究，2004（4）：44-47.

[5]王 宇，邵孝侯，李玉华.参考作物需水量实时预报方法研究进展[J].安徽农业科学，2008，36（3）：13 919-13 920.

S311

A

1008-0120（2017）02-0016-03

2017-05-18

郭志忠（1973-）：男，工程师；通讯地址：太原市上兰街办汾泉路1号，030051。