弦切角定理在圆弧曲线定位中的应用分析

杜开福（重庆建工集团股份有限公司，重庆400052）

弦切角定理在圆弧曲线定位中的应用分析

杜开福
（重庆建工集团股份有限公司，重庆400052）

0 引言

建筑施工放线是建筑施工的第一道工作，也是一道极为重要的工作，采用什么样的方法施工放样，既方便又精确也是非常重要的。随着各种建（构）筑物设计图形及造型日益复杂，例如圆弧形、椭圆形、双曲线、抛物线形以及正多边形等[1]，给定位放样提出了新的课题。这里介绍圆弧曲线定位放样中的一种方法，在圆弧曲形建筑定位测量中一般采用的方法有坐标法、矢高法和角度法等，但笔者在多个工程实践中进行比较认为，弦切角定理定位圆弧曲线的方法在已知圆心、半径、某一角度情况下颇为简易、方便、精确。现以重庆移动公司总部大楼为例，对该方法结合工程实例进行分析。

1 弦切角定理在圆弧曲线中定位放样

1.1 工程特点

重庆移动公司总部大楼位于重庆市北部新区高新技术开发区，是一幢综合性办公大楼，外观造型讲究，圆弧较多，该楼建筑总面积33000㎡，地下2层，地上18层，建筑总高度近88.7m，平面布置详见图1。该工程圆弧形共有6处，圆弧放样工作多、难度大；工期短，分两个施工段，所以圆弧定位放样快捷、准确的方法就至关重要。

鉴于上述情况，笔者结合该工程的特点选用了弦切角定理来定位圆弧曲线的放样。

1.2 原理[1]

弦切角等于该弧所对圆心角的一半，如图2。

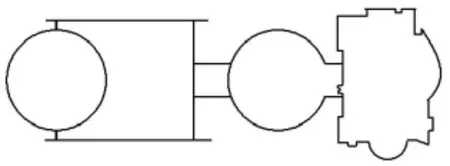
图1 重庆移动总部大楼平面示意图

图2 弦切角定理示意图

即：∠O''AB=1/2∠AOB=a/2

AB=2RSina/2

AC⊥OB，则AC=2RSina

AO⊥O”O’。

1.3 适用条件

（1）圆心、半径已知；

（2）某点切线可得；

（3）图纸中注明某一角度，圆心位置、半径。

1.4 测设步骤

以半径为15400mm、圆心角为88°的圆弧曲线定位、放样为例。

（1）方法一（如图3）

图3 以等分点为仪器测站点示意图

表1 各点弦长及弦切角

计算测量数据：将圆弧分为22等分（等分点越多所测曲线精度越高，但移动仪器次数也越多）计算出每一等分点间所对应之圆心角及弦长

圆心角：a=88°/22=4°；

弦长：AB=2RSina/2=2×15.4×Sin2°=1.075m。

测设方法：先将仪器置于0’点，后视直线部分G点，顺时针转动一个角度，既平角或弦切角a/2=180-2=178，在视线方向量取弦长1.075m定出C点，再将仪器移于C点后视O’点，顺时针转动一个角度，使其等于平角减2倍弦切角，这次后视的不是直线部分，而是弧弦方向a=180-4=176，在视线方向量取1.075m，定出D点。其余各点依次类推，直至22个等分点全部测出为止。这种方法仪器移动多比较麻烦，且易产生累计误差，笔者在实际放样定位时采用的以下方法。（2）方法二（如图4）

将仪器安置在所定位圆弦曲线中点，AC= 2RSina/2，弦长AD=2RSina，AE=2RSina3a/2。测设方法：将仪器置于O’点，后视直线部分G点顺时针转动（180-2）=178，在视线方向量取1.078m定出C点，将望远镜再顺时针转动一个弦切角（180-4）=176，在视线方向量取2.148m，定出D点，其余各点依次类推，最后定出B点。再将仪器以O’点为测站不变，后视直线部分K点，顺时针转动（180+2）=182，在视线方向量取1.075m，定出C’点，将望远镜再顺时针转动一个弦切角（182+2）=184，在视线方向量取2.148m定出D’点，其余各点依次类推，最后定出B’点。然后，将各点依次圆滑连结

起，这样就把圆弧曲线定位放样在实地上了。为了提高圆弧上的各点精度，笔者采取正、倒镜法取中来减小误差。

图4 仪器测站点为一个示意图

上述方法二是我在重庆移动公司总部大楼和多个工程定位放样圆弧曲线的实践总结的经验，这种方法移动仪器少，定位效率比方法一提高很多，并且精度也相应提高。

2 注意事项

（1）为提高测设精度，圆弧线等分点越多越好，并分别计算出各等分点对应的圆心角、弦切角及弦长，等分点应根据精度而确定，上述两种方法因地制宜。

（2）为提高圆弧线上各点（A、C、D……B）的精度，可采用正、倒镜法取中以减小测角误差[2]。

（3）测设的仪器选择J2级经纬仪或全站仪。

（4）利用经纬仪配合丈量工具放线时，经纬仪及丈量工具都必须是经过检验合格后才能使用，丈量时注意斜距改算成为平距，减少丈量误差，消除或减弱对测量精度的影响[2]。

3 结论

（1）用弦切角定理来定位圆弧曲线放样对仪器要求不很高，在放样时有足够的等分点精度上就能保证，能满足规范要求，并且简易、方便、快捷，实用性较好，特别是对于大圆弧，采用旋切角定理配合全站仪放样就更具有推广价值。

（2）两种弦切角定理定位圆弧曲线的方法若安置一次仪器测这么多点丈量有困难，或遇通视有困难时可把以上两种测设方法结合起来，每安置一次仪器应尽量多观测些等分点，既便于丈量、观测，又减少仪器移动的次数。

（3）为了提高曲线的定位精度，测角时应采用正、倒镜，若两次测得的点位置不同，检查无错误时应取平均值作为测量成果，通过重庆移动公司总部大楼竣工验收表明，圆弧曲线的定位放样精度完全达到规范细部轴线的要求。

（4）近年来我国大型的、复杂的、特殊的建筑（构）筑物不断出现，各种复杂的圆弧曲线越来越多，对于圆弧曲线定位放样测量提出了快捷、精确的要求。所以，研究和推广那些精度高、方法简便、速度快的圆弧曲线定位放样方法具有非常重要的意义。

[1]邓学才.复杂建筑施工放线[M].北京：中国建筑工业出版社，2007：1，62.

[2]胡伍生，潘庆林，黄腾.土木工程施工测量手册[M].北京：人民交通出版社，2005：65-68.

责任编辑：孙苏，李红

Analysison Application of A lternate SegmentTheorem in CircularCurve Positioning

平面图形比较复杂的工程，它的定位放线工作就非常困难，难以按设计图纸形状和尺寸直接进行放线测设，通常要运用一定的数学原理，进行一定的测设数据计算，将设计图纸上的尺寸变换成放线测量所需要的数据，利用测量仪器配合丈量式工具，采取一定方法测设出相应放线点，将各点依次圆滑连结起来，这样就把圆弧曲线定位放样在实地上了。该文结合建筑施工实例，介绍了弦切角定理怎样运用于圆弧曲线的定位和放样，通过实践表明这种方法简易、方便、准确。

弦切角定理；圆弧曲线；定位放线

It isvery difficult for the location and layoutof theprojectw ith complicated planegraphics,because it ishard to directly carry outaccording to the shapesand sizesof theoriginaldesignmaps.Usually,somemathematicalprinciplesare required for relevantdata calculation.The sizeson the design map have to be converted to the data required for the layoutmeasurement,w ithmeasuring instruments and tools,the corresponding layout points are measured,linking these points to a circular curve,thus the curve is presented on the ground.This paper,combined with practical construction cases,introduceshow alternate segment theorem isapplied to the location and layoutof circular curve and proves it simple,convenient and accuratew ith practices.

alternatesegment theorem;circular curve;location and layout

TU74

A

1671-9107（2017）07-0054-03

10.3969／j.issn.1671-9107.2017.07.054

2017-04-24

杜开福（1959-），男，重庆人，本科，高级工程师，从事建筑施工技术工作。