基于序列特征组合与核非线性回归预测蛋白质折叠速率

王雅男，白凤兰，刘立伟，王华

(大连交通大学 理学院，辽宁 大连 116028)

基于序列特征组合与核非线性回归预测蛋白质折叠速率

王雅男，白凤兰，刘立伟，王华

(大连交通大学 理学院，辽宁 大连 116028)

选取可压缩性、LZ复杂度等特征值，将它们和20种氨基酸属性Ca,K0,Pβ,Ra,ΔASA,PI,Ht,Mμ,Esm进行组合，表征蛋白质序列 .建立多元核非线性回归模型，用核非线性回归模型计算了 83个蛋白质的折叠速率预测值 .由 Jack-knife检验方法得知在不同的结构中不同组合特征值与相应折叠速率有较好的相关性 .实验结果表明：多元核非线性回归模型其预测精度及可行性高于线性回归模型，计算复杂度低和方便易操作等优点，具有良好的应用前景 .

核非线性回归；特征组合；蛋白质序列；相关系数；折叠速率

0 引言

蛋白质是生命活动的主要承担者，是生命的物质基础，也是构成细胞的基本有机物.自然状态下，蛋白质能从未折叠状态到达其特定的具有三维结构的天然构象.蛋白质折叠是一个非常复杂的过程，许多国内外科研工作者对蛋白质折叠速率问题进行了深入研究，不仅发现了很多影响蛋白质折叠速率的参数还相继提出各种预测蛋白质折叠速率的方法.已有预测方法的关键步骤：首先利用序列结构特征和氨基酸的物化性表征蛋白质，其次建立回归模型.例如，用接触序CO、总接触序ACO和有效接触序ECO等[1-3]表征蛋白质的预测方法，但是不能进行快速预测因为需要用到周期长、成本高的三级结构信息.用二级结构含量SSC、有效长度Leff等[4-5]表征蛋白质的预测方法，但是受到二级结构的限制[6-10]因为需要通过分子实验或者通过一级序列预测才能得到二级结构信息.用蛋白质肽链长度、氨基酸的物理化学性质、氨基酸的组成信息、氨基酸相互作用[11-14]表征蛋白质的预测方法，但是这些信息对蛋白质折叠速率的研究不全面,因为蛋白质结构非常复杂.蛋白质按折叠类型分为二态、多态和混态三种，按结构类型分为全α、全β、混合型三种[15-16].考虑到蛋白质折叠具有复杂性、非线性和不确定性，本文选取和蛋白质折叠速率相关性比较好的蛋白质序列的多种特征值，在已有的蛋白质序列的特征参数值对蛋白质折叠速率基础上，提出了基于MATLAB技术的支持向量回归机(SVR)模型对蛋白质折叠速率进行预测.首先将蛋白质进行分类，然后通过核非线性回归求出拟合的最佳参数，进而求出预测值.再通过Jack-knife检验的方法从多方面验证蛋白质序列的特征值对蛋白质折叠速率的影响.

1 材料和方法

1.1 材料

本文从Gromiha[17]文中提取83个蛋白质,在PDB 数据库(http://www.rcsb. org/pdb/home/home.do)中查到相关的氨基酸序列.含有39个未分类的蛋白质和44个已分类的蛋白质.44个已分类的蛋白质包含全类蛋白质13个，全类蛋白质18个，混合类蛋白质13个.

1.2 提取序列特征值

首先，提取20种氨基酸的一些属性：α螺旋接触面积Cα，可压缩性K0，β折叠趋势Pβ，在溶剂中的收缩率Ra，溶剂可及表面积ΔASA，氨基酸的等电点PI(25℃)，热力学疏水性转移Ht，折射率Mu，短程和中程非保税能源Esm等.

其次，将组成蛋白质序列的氨基酸属性标准化和平均化.

计算公式：

(1)

其中,氨基酸属性中的最小值和最大值分别为Pmin和Pmax，氨基酸的标准化属性为Pnorm(i)，氨基酸序列中第i个残基的属性为P(i).

计算公式：

(2)

其中,氨基酸序列中第j个残基的属性为P(j)，氨基酸序列的残基数为N，蛋白质的氨基酸平均属性为Pave.

利用氨基酸的标准化式(1)计算出20个氨基酸属性的值.用式(1)、(2)和20个氨基酸标准化后的值利用MATLAB分别计算39个未分类蛋白质以及13个全α类蛋白质，18个全β类蛋白质和13个混合类蛋白质的特征值，得到的数据多文中没表示.

最后，计算了83个蛋白质序列的序列复杂度[7,18].

计算公式：

(3)

其中,序列为S，序列S的复杂度为c(S).

1.3 方法

1.3.1 核非线性回归 (SVR)模型

核函数主要有四类，分别是：线性核函数(linear kernel)、多项式核函数(ploynomial kernel)、径向基核函数(radical basis kernel)、神经元的非线性作用核函数(neurons nonlinear interaction kernel).虽然一些实验表明在分类中不同的核函数能够产生几乎同样的结果，但在回归分析中，不同的核函数往往对拟合结果有较大的影响.通过大量实验本文选择径向基函数(RBF)作为核函数.基于序列特征与全部样本构建核非线性回归(SVR)模型[19-22].

用Matlab程序算法和SVR_GUI界面可以快速的得到预测结果.为了尽可能得到最好的预测准确度，选择使用网格搜索策略选择参数c和g的值，并对每一个数据集，基于5倍交叉验证，当参数寻优完毕后，得到bestc和bestg，当训练和预测完毕后得到蛋白质折叠速率的预测值和均方误差与相关系数.

1.3.2 模型评估

由于已知折叠速率的蛋白质样本数量较少,采用Jack-knife检验进行模型评估.评价指标为折叠速率预测值与实验值间的相关系数r和标准误差σ：

2 结果与讨论

用SVR模型分别计算了13个全α类蛋白质、18个全β类蛋白质、13个混合类蛋白质和未分类的39个蛋白质的10种特征值与折叠速率之间的相关性.特征值的不同组合，使实验值与预测值之间的相关性有好有坏，即10种特征值当中某些特征值组合对蛋白质的折叠速率没有影响，为此经过多次试验可知，特征值组合Cα,Ra,LZc,Ht对于全α类蛋白质折叠速率有影响；特征值组合K0、Pβ、ΔASA、LZc、PI对于全β类蛋白质折叠速率有影响；特征值组合K0,ΔASA,PI,对于混合类蛋白质折叠速率有影响；特征值组合K0、Ra、ΔASA、Mu、Esm对于未分类的蛋白质折叠速率有影响.用SVR模型得出实验值与预测值之间的相关系数分别为0.88,0.91,0.99,0.99，均方误差分别为2.165 08、1.141 29、0.010 033、0.159 45.实验值与预测值之间的关系直观图分别为图1所示.

(a) 未分类蛋白质

(b) α类蛋白质

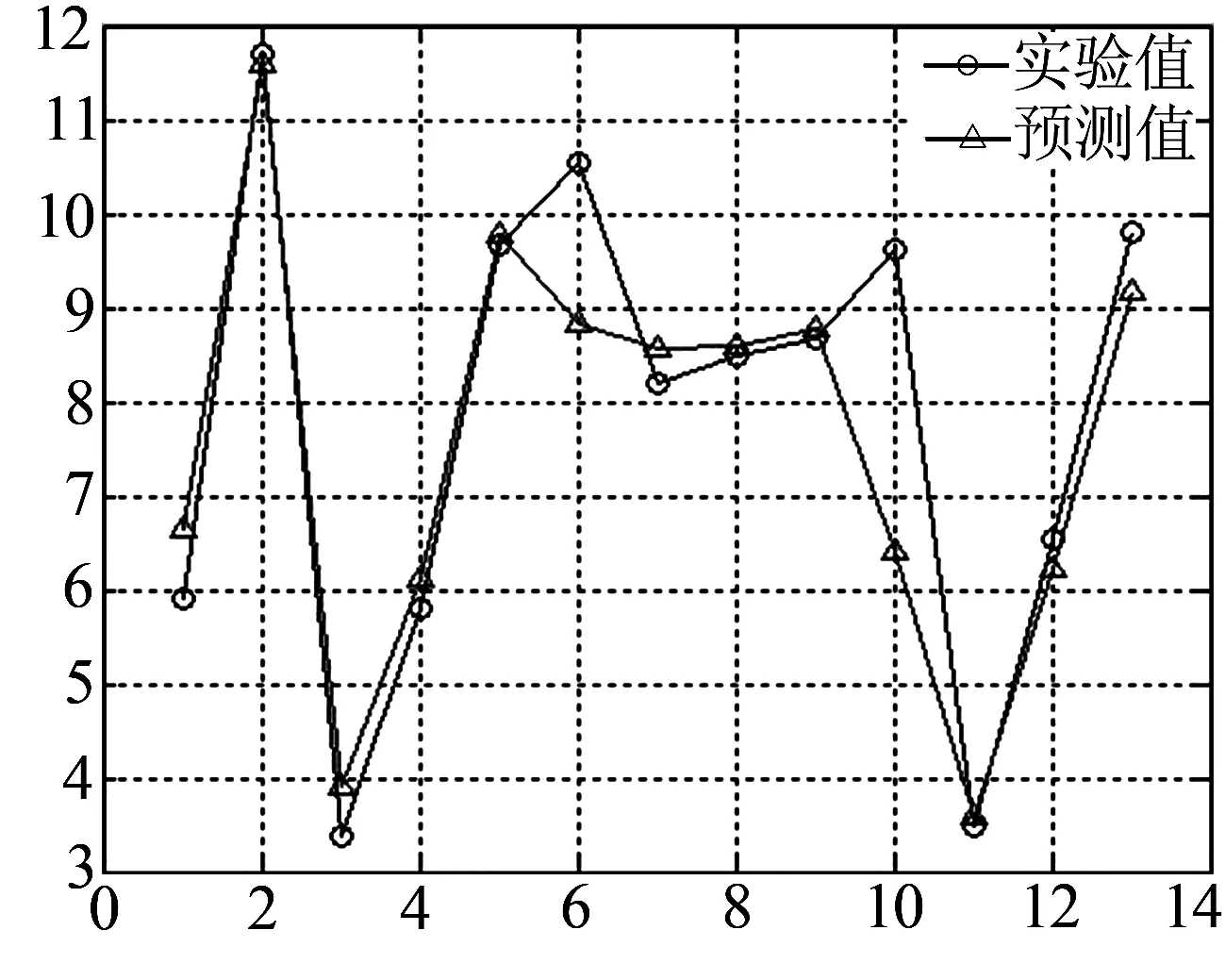
(c) β类蛋白质

(d) 混合类蛋白质

为了验证核非线性回归方法的可靠性，本文在已有的数据基础上又寻找了一些其它属性的数据，经过多次试验，对于未分类蛋白质、全α类蛋白质、全β类蛋白质、混合类蛋白质选取了以上所述的特征值分别进行核非线性回归，将得出的结果用Jack-knife方法进行检验并与 Gromiha方法的结果进行比较，发现相关系数都比其有所提高,见表 1.另外，由直观图 1也可知，用本文的方法得到的预测值与蛋白质折叠速速率实验值具有良好的相关性.

由表1可见，两种方法中特征值组合不尽相同，经过多次试验，选取了使实验值与预测值具有最好的相关性的特征值组合.不论在我们的方法和Gromiha方法中，可压缩性除全α类蛋白质外，对于其它类型的蛋白质折叠速率均有影响，其次，在溶剂中的收缩率除全α类和混合类蛋白质外，对于其它类型的蛋白质折叠速率也均有影响；在我们的方法中，序列复杂度LZc对全α、β类的蛋白质折叠速率有影响，短程和中程非保税能源Esm、只对未分类的蛋白质有影响.由此可知，特征值的不同组合，对蛋白质折叠速率的影响大小不同.经多次实验得知，基于序列特征组合建立的SVR模型非线性回归很显著.经Jack-knife检验可知蛋白质折叠速率预测值与实验值ln(kf)有良好的相关性，获得了优于Gromiha方法的预测精度.

表1 蛋白质核非线性回归分析结果比对

3 结论

组成蛋白质的20种氨基酸的物理化学属性有很多种，其中哪些属性对不同类别的蛋白质折叠速率预测有影响是本文研究的关键所在.本文提取13个全α类蛋白质、18个全β类蛋白质、13个混合类蛋白质和未分类的39个蛋白质的10种特征值，用核非线性回归方法和Jack-knife检验进行多次特征组合验证，特征值K0、Ra、 ΔASA、Mu、Esm，对于未分类的蛋白质折叠速率有影响，特征值Cα,Ra,LZc,Ht对于全α类蛋白质折叠速率有影响，特征值K0、Pβ、Ra、ΔASA、LZc、PI对于全β类蛋白质折叠速率有影响，特征值K0,ΔASA,PI,对于混合类蛋白质折叠速率有一定的影响.而这种特征组合得到的结果优于Gromiha方法的结果.

蛋白质折叠是一个非常复杂的过程.本文只是研究蛋白质的一级结构信息对蛋白质折叠速率的影响，运用生物信息学的方法，选取了蛋白质编码序列的一些特征值，通过实验验证了这些特征值对不同类别的蛋白质折叠速率的影响不同.不同的样本集对研究结果有一定的影响，因此需要大量样本验证支持.

[1]GALZITSKAYA O V, GARBUZYNSKIY S O, IVANKOV D N, et al. Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics[J]. Proteins: Structure, Function, and Bioinformatics, 2003, 51(2): 162-166.

[2]IVANKOV D N, FINKELSTEIN A V. Prediction of protein folding rates from the amino acid sequence-predicted secondary structure[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(24): 8942-8944.

[3]IVANKOV D N, BOGATYREVA N S, LOBANOV M Y, et al. Coupling between properties of the protein shape and the rate of protein folding[J]. PLoS One, 2009, 4(8): 6476.

[4]CHANG L, WANG J, WANG W. Composition-based effective chain length for prediction of protein folding rates[J]. Physical Review E, 2010, 82(5): 051930.

[5]MA B G, GUO J X, ZHANG H Y. Direct correlation between proteins' folding rates and their amino acid compositions: an ab initio folding rate prediction[J]. Proteins: Structure, Function, and Bioinformatics, 2006, 65(2): 362-372.

[6]MA B G, CHEN L L, ZHANG H Y. What determines protein folding type? An investigation of intrinsic structural properties and its implications for understanding folding mechanisms[J]. Journal of molecular biology, 2007, 370(3): 439-448.

[7]HUANG J T, XING D J, HUANG W. Relationship between protein folding kinetics and amino acid properties[J]. Amino acids, 2012, 43(2): 567-572.

[8]LIN G N, WANG Z, XU D, et al. SeqRate: sequence-based protein folding type classification and rates prediction[J]. BMC bioinformatics, 2010, 11(Suppl 3): S1.

[9]GROMIHA M M, THANGAKANI A M, SELVARAJ S. FOLD-RATE: prediction of protein folding rates from amino acid sequence[J]. Nucleic acids research, 2006, 34(Suppl 2): 70-74.

[10]HUANG L T, GROMIHA M M. Analysis and prediction of protein folding rates using quadratic response surface models[J]. Journal of computational chemistry, 2008, 29(10): 1675-1683.

[11]JIANG Y, IGLINSKI P, KURGAN L. Prediction of protein folding rates from primary sequences using hybrid sequence representation[J]. Journal of computational chemistry, 2009, 30(5): 772-783.

[12]OUYANG Z, LIANG J. Predicting protein folding rates from geometric contact and amino acid sequence[J]. Protein Science, 2008, 17(7): 1256-1263.

[13]LI H Y, WANG J H. Folding rate prediction using complex network analysis for proteins with two-and three-state folding kinetics[J]. Journal of Biomedical Science and Engineering, 2009, 2(8): 644.

[14]CHENG X, XIAO X, WU Z, et al. Swfoldrate: Predicting protein folding rates from amino acid sequence with sliding window method[J]. Proteins: Structure, Function, and Bioinformatics, 2013, 81(1): 140-148.

[15]HUANG J T, CHENG J P, CHEN H. Secondary structure length as a determinant of folding rate of proteins with two-and three-state kinetics[J]. PROTEINS: Structure, Function, and Bioinformatics, 2007, 67(1): 12-17.

[16]GALZITSKAYA O V, GLYAKINA A V. Nucleation-based prediction of the protein folding rate and its correlation with the folding nucleus size[J]. Proteins: Structure, Function, and Bioinformatics, 2012, 80(12): 2711-2727.

[17]GROMIHA M M. A statistical model for predicting protein folding rates from amino acid sequence with structural class information[J]. Journal of chemical information and modeling, 2005, 45(2): 494-501.

[18]LIU L, LI C, BAI F, et al. An optimization approach and its application to compare DNA sequences[J]. Journal of Molecular Structure, 2015, 1082: 49-55.

[19]VAPNIK V. The nature of statistical learning theory[M]. USA:Springer Science & Business Media, 2013.

[20]VAPNIK V, GOLOWICH S E, SMOLA A. Support vector method for function approximation, regression estimation, and signal processing[C]//Advances in Neural Information Processing Systems 9，1996.

[21]CASTRO NETO M, JEONG Y S, JEONG M K, et al. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions[J]. Expert systems with applications, 2009, 36(3): 6164-6173.

[22]YUAN Z. Better prediction of protein contact number using a support vector regression analysis of amino acid sequence[J]. BMC bioinformatics, 2005, 6(1): 248.

Protein Folding Rate Prediction based on Sequence Features Combined with Nuclear Non-Linear Regression

WANG Yanan ,BAI Fenglan ,LIU Liwei ,WANG Hua

(School of Mathematics, Dalian Jiaotong University, Dalian 116028, China)

Compressibility, LZ complexity and other characteristic values are selected and combined with twenty kinds of amino acid propertiesCa,K0,Pβ,Ra,ΔASA,PI,Ht,Mμ,Esmto characterize the protein sequence. Multiple nuclear non-linear regression model is established and used to calculate the folding rate prediction value of 83 proteins. By Jack-knife test, it is found that in different structures there is a good correlation between different combinations of characteristic values and the corresponding folding rate. The results show that the multiple nuclear non-linear regression model prediction accuracy and feasibility are higher than linear regression model, because it has the advantages of instancy low computational complexity and convenient and easy operation.

nuclear non-linear regression; combinations of features; protein sequences; correlation coefficient; folding rate

1673- 9590(2017)04- 0206- 05

2016- 04-11

王雅楠( 1990- ),女，硕士研究生；白凤兰(1963-)，女，教授，博士，主要从事生物分子信息学的研究E- mail:569594280@qq.com.

A