机械假腿的建模与PID控制

王欣立，葛研军

(大连交通大学 机械工程学院，辽宁 大连 116028)

机械假腿的建模与PID控制

王欣立，葛研军

(大连交通大学 机械工程学院，辽宁 大连 116028)

由拉格朗日方程建立了机械假腿动力学模型.设计了基于无刷直流电机的机械假腿PID运动控制系统，给出了PID参数的整定方法，并用Simulink仿真软件对机械假腿运动系统进行了仿真，仿真结果表明，基于此参数整定的PID控制机械假腿运动系统具有好的步态跟随特性.

机械假腿；PID控制器；仿真

文献识别码：A

0 引言

对于那些截肢患者来说，在日常生活中保持平衡是件很困难的事情.一些潜在的疾病，例如中风，也可以导致自身的行动不便，这些都会给患者的日常生活中带来很大的影响[1].对于腿部截肢患者，安装机械假腿可以帮助他们更好的生活.本文分析人类的步态形式，根据拉格朗日方程建立了机械假腿的动力学模型，设计了基于无刷直流电机驱动的机械假腿PID运动控制系统，给出了PID参数整定方法，并用Simulink仿真软件对机械假腿运动系统进行了仿真，仿真结果表明，机械假腿运动系统有好的步态跟随特性.

1 步态形式

人类的步态是具有周期性的，通常情况下，人类的行走步态可以分为支撑相和摆动相，而支撑相和摆动相又可以分为支撑屈曲，支撑伸展，摆动屈曲，摆动伸展.虽然这四相并不是固定的，但是它们可以很好地体现一个步态循环，并且这四个模式可以很好地用于定义和测量.人类的行走是最基本的运动环节.在正常行走时，膝关节的角度变化可以很好地体现人腿的角度变化.图1为人类膝关节角度表示，图2为正常步态下膝关节角度变化和正常步态的阶段划分[2].

图1 人类膝关节角度表示

当处于站立支撑阶段时，膝盖弯曲，脚后跟触及地面，身体的重量转向腿部，从而带动小腿向后运动直至脚准备离开地面.当处于摇摆阶段时，脚离开地面时膝盖从而摇摆，当脚准备再次触及地面时将开始另一个循环.

图2 正常步态的阶段划分和膝关节角度变化

2 动力学模型的构建

人腿结构可以被简化成一种双连杆结构，大腿和小腿分别由两刚性杆结构体现.图3为机械假腿原理图，假设两杆结构的质心和关节的旋转中心不变，且忽略躯干的质量.

图3 假腿原理图

图中，m1和m2分别为两连杆的质量，r1和r2分别为关节到质心的距离，L1和L2分别为两连杆的长度.θ1和θ2分别为大腿与小腿相对于y轴的角度位置，膝关节角度θk=θ1-θ2.

图4 假腿受力图

图4为假腿的受力示意图，T1和T2分别为髋关节和膝关节的承受的转矩.设笛卡尔坐标系下两连杆的质心坐标为(x1y1)，(x2y2)，髋关节的坐标为(xaya).则由图中可以得到各坐标值的关系表达式：

(1)

(2)

式(1)和式(2)的一阶导数为：

(3)

(4)

本文采用拉格朗日法构建机械假腿的动力学模型[3].设假腿机构的动能为W，假腿机构的势能为E，则拉格朗日函数L表达式为：

(5)

对于图3假腿结构，假腿机构的动能可以表示为：

(6)

式中，J1，J2分别为大腿和小腿在质心位置的转动惯量.

对于图3假腿结构，假腿机构的势能可以表示为：

(7)

式中，g为重力加速度.

机械假腿的力矩表达式如下：

(8)

式中,Ts为力矩.θ为各躯干角度.将式(6)和式(7)代入式(5)，再将式(5)代入式(8)；得到机械假腿的力矩表达式如下：

(9)

(10)

(11)

(12)

(13)

髋关节力矩T1和膝关节力矩T2表达式为：

由式(14)和式(15)可以看到，髋关节和膝关节的承受的力矩是随着θ1和θ2的改变而改变.

3 机械假腿运动系统设计和仿真

图5为机械假腿运动系统结构框图，由于在正常行走时，膝关节的角度变化可以很好地体现人腿的角度变化.因此可以构建一个两自由度运动控制系统，实现机械假腿膝关节的角度变化，模仿人类步态运动过程.图中θ1d和θ2d为由给定步态计算得到的大腿和小腿输入角度，θ1a和θ2a分别为大腿和小腿的输出角度.机构负载转矩为髋关节力矩T1和膝关节力矩T2，采用两台无刷直流电机作为执行机构，执行机构通过减速器齿轮箱(减速比80∶1)拖动负载运行，控制器采用PID控制.

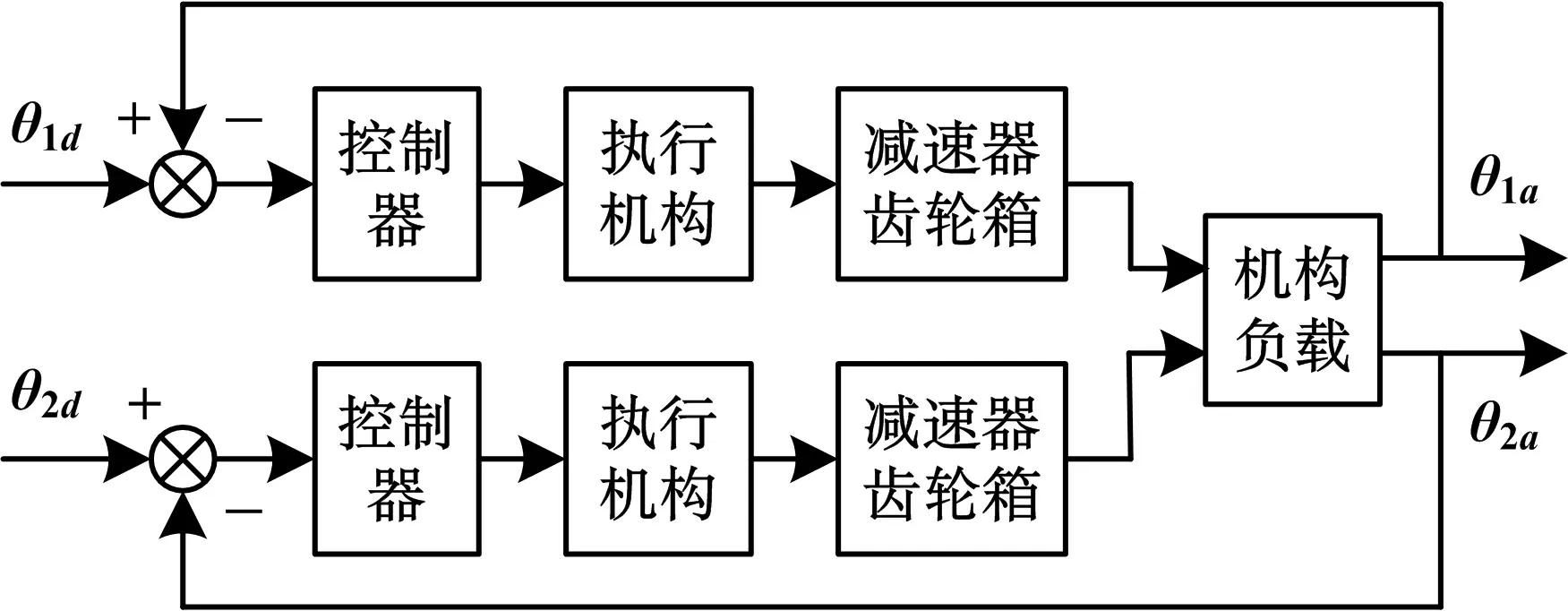
图5 机械假腿运动系统结构框图

PID控制，又可称之为比例、积分、微分控制，其控制规律为：

(18)

其原理图如图6所示.

图6 PID控制原理图

其中，u(t)为控制输出量，根据给定值r(t)和实际输出值c(t)可以得出偏差信号e(t)=r(t)-c(t) .对于PID控制器，其比例(P)相是指对偏差的放大倍数，通过增大比例相可以增加其对偏差的放大倍数，从而使得误差逐渐减小，而其比例放大倍数对于控制作用的强弱有着至关重要的作用，但是过度增大比例系数会使闭环系统趋于不稳定，动态性能差.积分(I)相是指对偏差值在时间上进行累加，只要误差一直存在，积分就会不断累加，通过很好地调节积分相可以使得输出值达到预设值，从而消除稳态误差.如果积分效果太强，系统会出现震荡，从而使得闭环系统不稳定，动态性能变差.微分(D)具有超前作用，其根据偏差的变化速率，提前给出对应的调节，通过解析偏差值来防止输出值过度的震荡，提高系统的稳定性，减小调节时间，加快系统的动态响应速度.

机械假腿控制系统PID参数的整定采用Ziegler and Nichols 第二法进行.Ziegler and Nichols又称为连续振荡法.首先设置积分系数和微分系数为0，只加比例环节，直到闭环系统达到临界发散时记录此时的比例增益值Ku和振荡周期Tu，根据比例增益值Ku和振荡周期Tu，可以由表1计算出PID参数[5].

表1 Ziegler and Nichols整定PID参数法

机械假腿运动系统两自由度运动控制系统构成，由式(14)和式(15)可以看到，负载转矩不是恒定值，而是随着θ1和θ2的变化而变化.对于两通道PID控制器参数整定作如下处理，设θ2=0时，对于θ1通道进行PID参数整定；设θ1=0时，对于θ2通道进行PID参数整定，将此整定参数带入系统进行控制，观察机械假腿运动系统的跟随特性.系统的PID参数整定由Simulink仿真软件构建的系统仿真模型系统确定，表2所示为假腿的模型参数.

表2 假腿模型参数

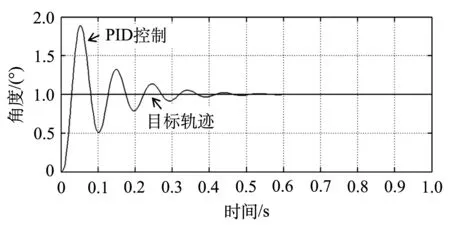
图7(a)为θ2=0时大腿θ1闭环系统临界状态的仿真曲线.此时，大腿控制器比例增益Ku=4.23，振荡周期Tu=0.09 s，由表2确定的PID参数为：Kp1=2.54，Ki1=56.41，Kd1=0.029.图7(b)为θ1=0时小腿θ2闭环系统临界状态仿真曲线.此时，小腿控制器比例增益Ku=2.092，振荡周期Tu=0.076 s，由表2确定的PID参数为：Kp2=1.255，Ki2=27.287，Kd2=0.014.

(a)大腿θ1

(b)小腿θ2

(a)大腿θ1

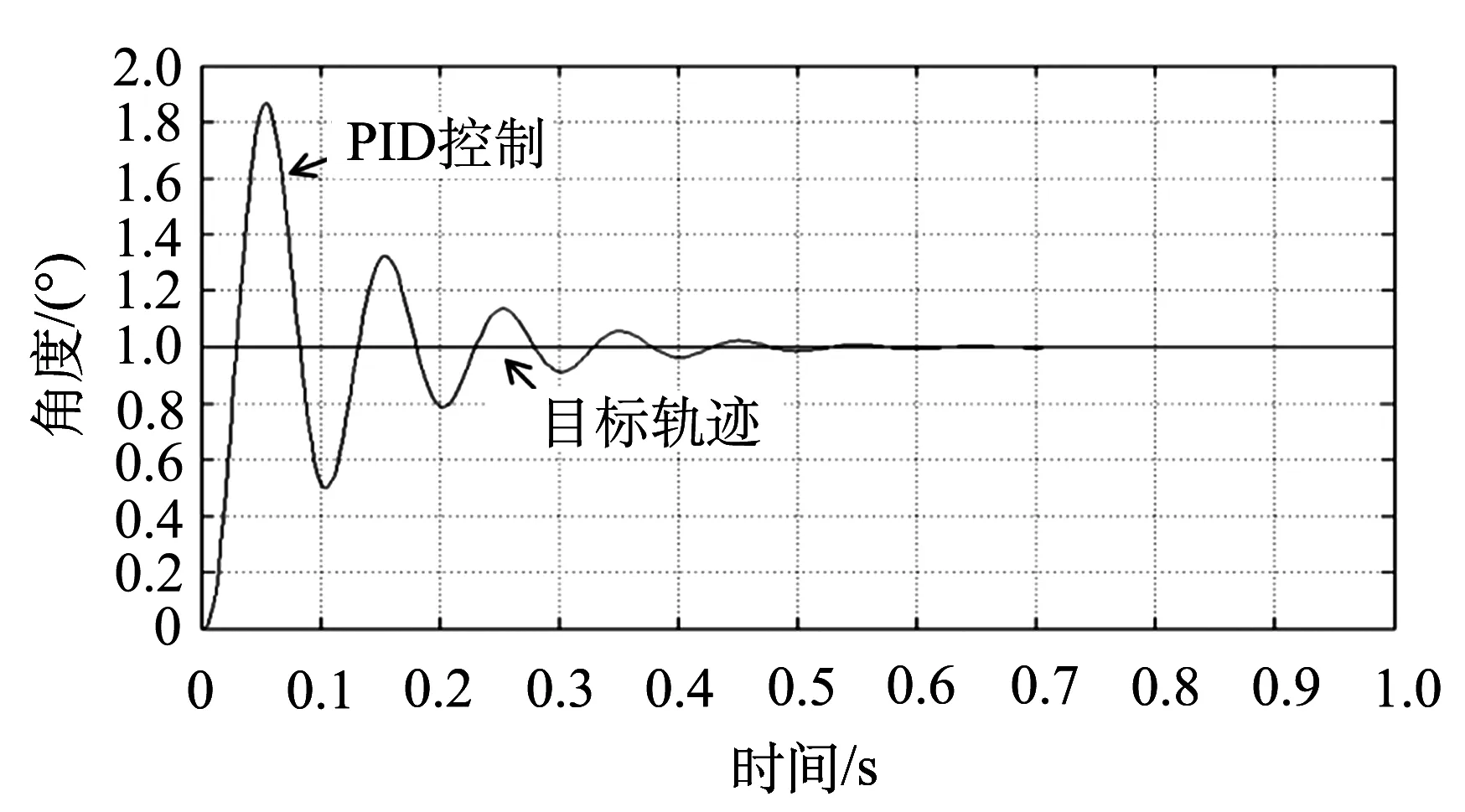
(b)小腿θ2

人类步态的转化很快，一般情况下，正常男性的迈一步的速度大约为1.56 s，要求系统响应要快，并能跟随正常步态[6].图8(a)为θ2=0时大腿相对于y轴的角度θ1的单位阶跃响应特性仿真曲线，图8(b)为θ1=0时小腿相对于y轴的角度θ2的单位阶跃响应特性仿真曲线.从图中可以看到，单位阶跃响应的上升时间和过渡过程时间较小.

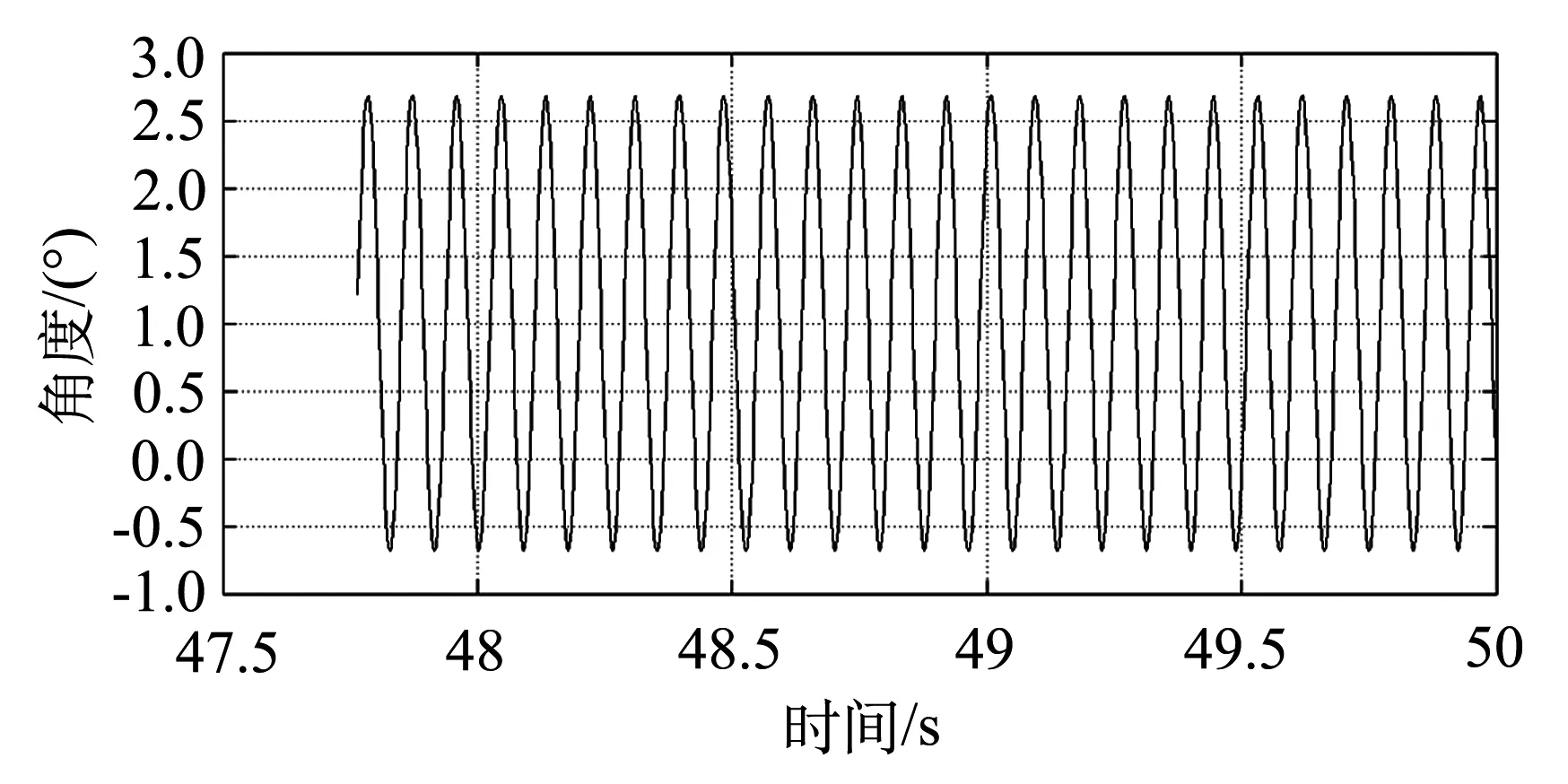
将上述整定方法得到的PID参数带入机械假腿运动系统进行控制，得到的膝关节角度跟随特性如图9所示，从图中可以看到，对于给定的正常步态下膝关节角度变化曲线，其膝关节角度有好的跟随特性，由此看来，上述方法整定得到PID参数，可以满足机械假腿运动控制系统的要求.

图9 膝关节角度跟随特性曲线

4 结论

对于那些截肢患者来说，安装辅助机械可以使他们的生活达到改善，并且在日常生活中的影响越来越重要.本文对机械假腿进行了研究，分析人类的步态形式，构建了机械假腿的动力学模型，并以机械假腿为负载，设计了基于无刷直流电机驱动的机械假腿PID运动控制系统，给出了机械假腿控制系统的PID整定方法，仿真结果表明:机械假腿运动系统对于给定的正常步态下膝关节角度变化曲线有好的跟随效果.

[1]WU JUNPENG,JINWU GAO,RONG SONG,et al.The design and control of a 3DOF lower limb rehabilitation robot[J].Mechatronics，2016,33:13- 22.

[2]SUP FRANK,AMIT BOHARA,MICHAEL GOLDFARB.Design and Control of a Powered Transfemoral Prosthesis[J].The International Journal of Robotics Research,2008,27(2):263- 273.

[3]WINTER D A.Biomechanics and Motor Control of Human Movement[M].Hoboken：John Wiley & Sons Ltd，2009:45- 236.

[4]PINITLERTSAKUN,JUTAMAT,MAHESAK RACHAGORNGIJ,et al.Design of the prosthetic knee component to assist stair ascending gait[C].Biomedical Engineering International Conference (BMEiCON)，2013.

[5]董景新.控制工程基础[M].北京:清华大学出版社，2009:264- 267.

[6]ADENIYI,ADE FATAI,ABUBAKAR SADIK MOHAMMED,et al.Adverse relationships of adiposity and gait parameters:A survey of stroke patients undergoing rehabilitation[J].Hong Kong Physiotherapy Journal,2011,29(1):34- 39.

地铁直线段轮对横移量对轮轨磨耗的影响

张璘1,刘佳欢2,张军2,孙传喜1

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028; 2.北京建筑大学 机电与车辆工程学院，北京 100044)

摘 要：利用轮轨型面测量仪对北京地铁六号线轮轨型面进行现场实测，采用样条曲线拟合方法获得并选取磨耗轮轨型面，利用有限元分析软件ABAQUS建立四组轮轨三维有限元模型，计算并分析了不同轮对横移量下轮轨间接触斑和最大等效应力分布状态，研究轮对横移量对直线段轮轨磨耗的影响，分析结果表明：地铁直线段不同轮对横移量下标准轮轨接触斑较规则，多数非标准轮轨接触斑呈"斑条"状，接触斑面积一般在轮对横移量-8、4和6 mm时较大；轮对横移量8 mm处，标准车轮与磨耗钢轨接触应力过大，钢轨轨距角处易产生应力集中，发生塑性变形；不同轮对横移量下磨耗车轮/标准钢轨匹配接触斑面积较大，最大等效应力较小，对减缓轮轨磨耗十分有利.

Modeling and PID Control of Prosthetic Leg

WANG Xinli，GE Yanjun

(School of Mechanical Engineering,Dalian Jiaotong University，Dalian 116028,China)

A dynamic model of prosthetic leg is derived based on Lagrangian formulation,and a design of PID control system of prosthetic leg which is driven by brushless DC motor is proposed.Meanwhile,the PID controller tuning method of parameters is presented,and simulink simulation of the prosthetic leg is designed.The simulation results show that the PID control is good for gait tracking of prosthetic leg based on the PID controller tuning method.

prosthetic leg;PID controller;simulation

1673- 9590(2017)04- 0125- 05

2016- 11- 05

王欣立(1992-),男，硕士研究生；葛研军(1964-),男，教授，博士，主要从事机电传动方面的研究E-mail:510612440@qq.com.