基于代理模型的高速列车头型优化设计

周家林，包福明, 陈秉智

(1.中车四方车辆有限公司，山东 青岛 266111; 2.大连交通大学 交通运输工程学院,辽宁 大连 116028)

基于代理模型的高速列车头型优化设计

周家林1，包福明2, 陈秉智2

(1.中车四方车辆有限公司，山东 青岛 266111; 2.大连交通大学 交通运输工程学院,辽宁 大连 116028)

为降低高速列车的气动阻力，对高速列车流线型头尾进行优化设计.建立高速列车空气动力学模型，基于三维黏性不可压缩控制方程组和两方程湍流模型，对明线上运行的3节编组列车周围流场模拟计算.构造6个优化设计变量关于空气阻力的响应面函数.结果表明，各优化设计变量之间相互耦合，和优化目标之间存在非线性关系，同时得到了各设计变量对空气阻力的贡献率.优化后，空气阻力值降低10.8%.

气动优化；网格自动变形；响应面法；遗传算法

0 引言

列车气动阻力随列车运行速度而急剧增长，降低高速列车运行时的空气阻力可以提高列车运行的安全性，稳定性和经济性.高速列车所受气动阻力与列车头尾外形有密切关系，流线型外形的优化设计已成为高速列车的关键技术之一[1-2].

张在中[3]通过对包括CRH2在内的不同高速列车模型(1∶8)进行风洞实验，分析了列车流线型头部形状对阻力的影响.其阐述的方法实际上是优选方法，优选结果并不能达到或接近最优解.随着计算机软硬件的不断发展，Krajnovi[4]以径向基神经网络和多项式函数为组合代理模型，对列车的气动特性进行了优化.Yao[5]提出局部型函数的优化方法，对高速列车鼻部外形进行优化，其优化结果使列车气动阻力减小8.7%.Sun[6]采用直接网格变形技术，省去了几何重构和网格划分的时间，对高速列车司机室上壁面形状进行优化.熊骏[7]采用神经网络算法对城际列车外形进行优化.翟建平[8]考虑在横风载荷作用下对列车头型优化.刘加利等人[9]采用几何自动重建技术使流线型车头改变形状，使列车空气阻力降低.

本文在对CRH3高速列车参数化建模后，由拉丁超立方抽样法得到200组样本自变量值，通过集成批处理文件及脚本文件，实现网格自动变形及空气动力学自动计算，得到样本因变量值.再构造空气阻力关于设计变量的响应面代理模型.最后采用多岛遗传算法得到近似的全局最优解.上述过程不仅实现了一种空气动力学自动计算方法，而且可以通过响应面分析得到各设计变量与列车空气阻力的关系.实现了一种适于高速列车的外形降阻优化设计的方法，对于高速列车的降阻设计具有较好的工程应用价值.

1 控制方程

一般情况下，明线运行上的高速列车马赫数小于0.3[10]，在不考虑列车交会、列车过隧道等问题时，空气密度的变化对流动的影响极小，列车周围流场可以按照不可压缩粘性流动模型考虑.在此模型中，能量方程与连续性方程和运动方程不耦合，如果不计算温度场，则无需引入能量方程.不可压缩定常流动控制方程如下：

连续方程：

(1)

N-S方程：

(2)

式中，ui为流场速度，代表u、v、w三个坐标方向的速度分量；xi为三个坐标，代表x、y、z三个坐标分量；p为热力学压强；μ为空气动力粘度；ρ为空气密度.

高速列车周围流场为湍流流动，采用两方程模型来描述湍流流动.

定义湍流粘性系数为：

(3)

湍流动能方程为：

(4)

湍流耗散率方程方程为：

(5)

其中，k为湍流动能；ε为湍流耗散率;cμ为湍流常数，一般情况下取cμ=0.09；μl为层流粘性系数；c1、c2、σk、σε为经验常数，根据经验，计算时取值如下：c1=1.47，c2=1.92、σk=1.0、σε=1.33.以上方程组共含有7个未知数和7个方程，方程组封闭.给定边界条件后，可求解.

2 计算模型

2.1 参数化几何模型

由于数学上无法用单个解析方程刻画复杂空间曲面，于是采用具有连续阶的若干子曲面拼接成列车车头流线型曲面.由流线型车头表面的若干控制点生成若干条非均匀有理B样条曲线，再由这些空间曲线生成NURBS三维空间曲面.最后对控制点进行参数化处理，最终实现列车参数化几何建模.需要说明的是，由于是以高速列车流线型头型优化为目标，可以对列车底部平底简化处理[9].

2.2 数值模型

列车采用三节车(头车+中间车+尾车)编组，列车全长76.125 m.根据多次计算得知，当计算区域选择如图1所示的区域时,计算结果较为准确.

图1 计算流场区域

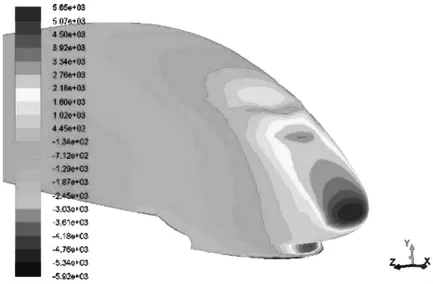
图2 车头表面压强分布

3 响应分析及优化结果

3.1 响应面代理模型

3.1.1 优化设计变量

为驱动列车流线型车头形状的变化，如图3所示，选取流线型车头上部12个控制点，其中每3个点间设置为主从关系，可以得到4个自变量，分别定义为dy1、dy2、dy3和dy4，控制列车头部垂向变形； 在车头两侧选取10个控制点，10个点设

图3 控制点布置

置为主从关系，可得到1个自变量，定义为dz5，控制列车流线型车头沿横向变形；在流线型车头前端部设置9个控制点，设置为主从关系，可得到1个自变量，定义为dx6，控制列车头部纵向变形.由于实际运行的列车头车和尾车外形相同，本文对尾车与头车的控制点做对称处理.

为了得到较大的寻优空间，同时考虑到直接网格变形技术容易导致网格畸变，自变量dy1、dy2、dy3、dy4、dz5和dx6的区间均定义为[-0.7m,+0.7m].在自变量的变化范围内，采用拉丁超立方抽样法得到200组样本自变量.其中dy1，dy2的散点分布如图4所示.

图4 dy1和dy2的分布

3.1.2 网格自动变形及CFD自动计算

数学上有了200组样本自变量后，需要得到每组自变量所对应的因变量.即物理上需要得到不同车头形状的编组列车在空气中运行时的空气阻力.为了去除人工的重复性工作，编写可对控制变量值进行修改的程序实现网格的自动变形.利用fluent的脚本文件实现高速列车空气动力学自动计算.最后利用批处理程序及isight软件平台将上述程序集成，实现网格自动变形及空气动力学的自动计算.

3.1.3 响应面分析

通过程序间集成自动计算得到了200个具有不同形状流线型车头编组列车的气动阻力值.即求得了因变量(气动阻力)分别对200组自变量(dy1、dy2、dy3、dy4、dz5和dx6)的响应.由这些样本，即可运用多项式响应面法(Response Surface Method)来构造代理模型.三次多项式响应面如图5所示.为了验证代理模型的准确性.选取其它10组样本对响应面代理模型进行R2分析，经计算模型的R2=0.992.R2接近1，表明响应面模型与样本符合程度高，构造的响应面模型准确有效.

图5 优化设计变量与目标的响应面

图6是所有因子相对优化目标即气动阻力的贡献率图(Pareto图).深色表示正效应，浅色表示负效应.由图可知，对于3节编组列车而言，头部及尾部纵向越长、横向越窄、垂向越扁则列车所受空气总阻力越小.dz5的贡献率达到65%，对气动阻力影响最大；dx6对气动阻力影响贡献率为22%；而dy4、dy3、dy1、dy2综合起来对气动阻力贡献率为13%.究其原因，由于原始模型已为流线型，当控制点早[-0.7m，+0.7m]范围内变化时，列车头部及尾部纵向长度的变化和垂向形状的变化并未改变头型尖端的尖锐程度.而头尾横向宽窄的变化，对流线型头型尖端部的尖锐程度影响较大，因而dz5对于空气阻力影响最大.同时可以看到dy4、dy3、dy1、dy2对气动阻力影响依次降低，这是因为dy4和dy3是流线型尾上表面几何突变位置，车体表面几何变化导致周围流场形成逆压梯度，同时由于粘性对速度的迟滞作用，综合作用导致涡旋的形成以及边界层分离现象.因而此处外形对流动影响较大.dy2离车头尖部最近，对车头尖锐程度有一定影响，但影响有限.

图6 各因子贡献率图

图7显示了dy1和dy2及dy1和dx6对气动阻力存在交互效应.由于交互效应图两条线并不完全平行，因此dy1和dy2及dy1和dx6分别耦合在一起对气动阻力F产生影响.究其原因，由于空气动力学问题是非线性问题，而非线性的实质是运动物质间的相互作用.物理上讲，作为亚音速低速空气流动，高速列车运动时，其产生的扰动会快速传播，头车、中间车以及尾车周围流场会相互作用，不仅列车头部周围流场会影响后部流场、后部流场可影响前部流场，而且每节车周围的流场内流体间也会相互作用.因此，dy1和dy2分别对流动产生影响，而这些被影响的流体间又相互作用，形成交互效应.这种交互作用的数学实质是空气动力学微分方程组中各变量之间的相互耦合.

图7 交互效应图

3.2 优化结果

采用多岛遗传算法(Multi-Island Genetic Algorithm)得到响应面的近似全局最优解.寻优过程如图8所示.优化前，列车所受总气动阻力大小为20 721.7 N，优化后列车所受总气动阻力大小为18 494.0 N.

图8 优化过程图

设计变量优化结果如图9所示.分析优化结果，控制列车横向形状的变量dz5值为-0.650 m，接近于寻优区间下限.控制列车流线型头型长度的变量dx6值为0.689 m，接近于寻优区间上限.以上两变量的优化结果使列车流线型头尾更细长，这与空气动力学的基本理论及工程经验相吻合.而控制列车头尾垂向形状的四个变量与列车气动阻力值并不是线性关系.优化结果符合对响应面函数的因子贡献率分析结论及因子交互效应分析结论，再次说明本文所构造的代理模型的准确性.同时可以看到，在以列车降阻为目的的工程实践中，对控制头型外形的参数的选取应经过慎重考虑，在工程经验确定车头外形大致轮廓的基础上，应采用科学技术手段对参数做最终确定.本文所述方法为一种有效途径.

图9 变量寻优结果

4 结论

对构造的响应面函数进行分析得到以下结论：

(1)列车空气阻力值和各控制变量间存在三次多项式函数响应关系；

(2)控制列车流线型头尾的各变量对列车阻力的影响并不是简单的线性叠加，而是各变量相互耦合在一起改变列车周围流场运动，进而改变列车阻力.列车阻力和各变量间是非线性关系；

(3)各控制变量对优化目标的贡献不同.dz5、dx6、dy4、dy3、dy1、dy2对改变气动阻力的贡献依次降低；

(4)优化后和优化前相比，列车阻力降低10.8%.

基于网格自动变形技术及空气动力学自动计算方法，结合响应面代理模型分析，实现三节编组高速列车外形的优化设计，可较好应用于高速列车的降阻设计工程实践.

[1]肖京平，黄志祥，陈立.高速列车空气动力学研究技术综述[J]. 力学与实践, 2013,35(2):1-12.

[2]杨国伟，魏宇杰，赵桂林，等.高速列车的关键力学问题[J]. 力学进展, 2015,45:217-305.

[3]张在中，周丹.不同头部外形高速列车气动性能风洞试验研究[J]. 中南大学学报, 2013, 44(6)：2603-2608.

[4]KRAJNOVI S. Shape optimization of high-speed trains for improved aerodynamic performance[J]. P I Mech Eng F-J Rai., 2009, 223: 439- 452.

[5]YAO S B, GUO D L, YANG G W. Three-dimensional aerodynamic optimization design of high-speed train nose[J]. Sci. China:Tech Sci., 2012, 55: 3118-3130.

[6]SUN Z X, SONG J J, AN Y R. Optimization of the head shape of the CRH3 high speed train[J]. Sci China:Tech Sci., 2010, 53: 3356-3364.

[7]熊骏. 城际列车气动外形优化研究[D]. 成都：西南交通大学,2012.

[8]翟建平. 气动载荷下高速列车动力性能及参数优化研究[D].成都：西南交通大学,2012.

[9]刘加利,李明高,张继业等.高速列车流线型头部多目标气动优化设计[J]. 中国科学:技术科学, 2013, 43(6): 689- 698.

[10]田红旗.列车空气动力学[M].北京：中国铁道出版社，2007.

高速列车车体可靠性参数灵敏度分析方法对比研究

向鹏霖1，卢耀辉1，党林媛1，冯振1，曾京2

(1.西南交通大学 机械工程学院，四川 成都 610031;2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

摘 要：以某型高速列车车体为研究对象，建立车体参数化有限元模型，将车体的材料属性、几何尺寸和载荷大小等参数设为随机变量，基于概率分析方法，通过统计分析得到其分布参数，分别基于蒙特卡洛和响应面数值模拟方法，求解车体的参数灵敏度。分析结果表明：在所选随机变量中，车体底架板材1、板材4和板材6的板厚尺寸对车体关注部位应力影响显著，设计过程中应对该变量进行严格控制；使用蒙特卡洛法和响应面法得到的灵敏度结果一致，其中响应面法缩减了求解时间；采用概率设计方法代替传统的定值设计方法，可以为高速列车车体的可靠性设计提供新的途径 .

Shape Optimization of High-Speed Train Head based on Response Surface Method

ZHOU Jialin1, BAO Fuming2, CHEN Bingzhi2

(1. CRRC Sifang Co., Ltd, Qingdao 266111, China; 2.School of Traffic and Transportation Engineering，Dalian Jiaotong University，Dalian 116028，China)

Shape optimization is used to reduce aerodynamic resistance of high-speed train. After building the aerodynamics model, flow field around the high-speed train is simulated based on three-dimension uncompressible equations and turbulent model of two equations. Response surface function of 6 design variables is established. Results show that the design variables are coupled with each other and optimization object is the nonlinear function of the variables. Contribution to air resistance of each variable is also calculated. Air resistance is reduced 10.8% after optimizing.

aerodynamic optimization; mesh automatic deformation; response surface method; multi-island genetic algorithm

1673- 9590(2017)04- 0083- 05

2016- 11- 28

中国铁路总公司科技研究开发计划资助项目(2015J007-H)

周家林(1972-)，男，高级工程师，硕士，主要从事车辆工程的研究E- mail:chenbingzhi06@hotmail.com.

A