过渡金属轻元素化合物高硬度多功能材料的设计∗
2017-07-31包括马帅领徐春红崔田
包括 马帅领 徐春红 崔田
(吉林大学物理学院,超硬材料国家重点实验室,长春 130012)(2017年1月13日收到;2017年1月19日收到修改稿)
专题:高压下物质的新结构与新性质研究进展
过渡金属轻元素化合物高硬度多功能材料的设计∗
包括 马帅领 徐春红 崔田†
(吉林大学物理学院,超硬材料国家重点实验室,长春 130012)(2017年1月13日收到;2017年1月19日收到修改稿)
过渡金属在元素周期表中占有特殊位置,它们有较多的价电子、较高的电子密度、丰富的价态,通过在其中引入硼、碳、氮等易形成强共价键的轻元素原子形成化合物,是寻找新型多功能材料的重要手段.随着第一性原理计算理论的发展、电子计算机计算能力的提升、对硬度微观机制的理解的深入以及特定条件下物质对应的结构的预测软件的成熟,使得设计过渡金属化合物高硬度/超硬度新型多功能材料成为可能,目前这方面已经有了大量的工作.本文介绍了以硬度为主要性能的新型过渡金属化合物的设计基础,以及过渡金属轻元素化合物的研究现状,并对存在的问题进行了简述,可为新型高硬度多功能过渡金属化合物的设计及合成提供参考.
材料设计,超硬材料,计算模拟,过渡金属化合物
1 引 言
超硬材料以其耐高压、抗磨损、化学性质稳定等特性,可作为切削、打磨、抛光等加工工具的材料和机械部件上的抗磨损涂层,在军事、工业等领域有重大用途.同时超硬材料往往具有良好的导热性、电学特性和光学特性,可应用于特殊工作环境.超硬材料从其机理上可以分为两类:第一类是本征超硬材料,即该种材料的理想晶体本身就具有很高的强度;另一类是非本征超硬材料,该种超硬材料主要是由晶界、缺陷、微观结构等非本征因素引起的.本文关注于前者,通过深入理解材料的微观晶体结构、电子结构、化学键等与硬度的关系,进而指导设计合成更多类型的、更多优异功能的超硬材料.
现在已知最硬的材料是金刚石(体弹性模量444 GPa,硬度60—120 GPa),其也是目前已知最好的导热材料和良好的p型半导体材料;第二硬的材料是在高温高压下人工合成的立方氮化硼(体弹性模量369 GPa,硬度32—50 GPa)[1].但是金刚石和立方氮化硼的应用都有一定的局限[2],因此,寻找新型的、生成条件温和的高硬度多功能材料一直是材料学、物理学、工程学的热点领域.
根据金刚石和立方氮化硼的特点,人们尝试在硼、碳、氮、氧等可以形成强化学键的轻元素组合中寻找新型超硬材料[3−5],如碳的高压相[6−8]、碳 -氮化合物[9−13]、硼 -碳[14]、硼 -氮[15−19]、硼 -氧[20]、硼-碳-氮[21]、硼-氮-氧[22]等相继被预言或合成.但是,它们依然存在合成条件比较苛刻、无法制备大尺度材料等缺点.
过渡金属通常有很高的电子密度,往往具有很高的体弹性模量,这为产生超硬材料提供了有力条件.但是,由于金属键的特性,其剪切弹性模量不高,所以不能成为超硬材料.比如金属锇,有很高的体弹性模量,可以和金刚石相比拟[23,24],但是其硬度与一般过渡金属相仿,比金刚石低两个数量级[25].小原子的硼、碳、氮、氧也有很高的电子密度,在大原子体系中引入小原子,可以防止原子发生移位,这是提高体系硬度的一个传统方法[26],同时这些原子可以和过渡金属生成化合物,产生共价键网络或方向很强的离子键,为寻找超硬材料提供了一个重要的思路[25−27].已有的过渡金属化合物WC已经是一种非常常用的硬质材料,但其硬度远小于超硬材料的标准.Chung等[28]用电弧方法合成出RuB2,OsB2,ReB2,测得它们的硬度分别为(19.2±2.1),(21.6±3.0),(37.0±1.2)GPa[29].ZrO2与HfO2的体弹性模量分别为444 GPa和340 GPa[30];TiO2在高温高压下形成PbCl2结构,其体弹性模量为431 GPa,硬度为38 GPa[31];有理论预测OsN4有高体弹性模量、高剪切模量以及小泊松比,是可能的硬材料[32].另外多元过渡金属化合物,比如V0.4Os0.6B2,Mo0.6Ir0.4B2,W0.56Ir0.44B2[33−35],都具有很高的价电子密度,是可能的超硬材料[25].由于材料中残存的金属键和离子键缺乏方向性,这些材料的硬度都达不到金刚石的硬度.在过渡金属化合物中建立强共价键网络并减少金属键,是新型超硬材料设计必须面对的巨大挑战.过渡金属的d,f轨道电子性质复杂,所以含过渡金属的化合物往往具有奇异的电子结构,表现出很多奇特的性质.例如,HfB2,ZrB2,TiB2表现出高硬度和高的热导率[36−38].过渡金属化合物是多功能超硬材料的富矿,尽管现在实验上并没有找到可信的硬度超过40 GPa的过渡金属化合物,但是有理由相信在过渡金属化合物中存在大量的高硬度多功能材料,等待我们继续深入探索发现.
本文首先讨论硬度的本质、超硬材料设计的基本理论及所应用的方法与工具;其次,列举了一些高硬度多功能材料设计的案例;再次,讨论超硬多功能材料设计与实验的比较和可能遇到的问题;最后,对过渡金属轻元素化合物高硬度多功能材料的设计进行了总结.
2 超硬多功能材料的设计基础
2.1 硬 度
正如O’Neill[39]在1934年所指出的:“Hardness,like the storminess of the seas,is easily appreciated but not readily measured”. 硬度是物体的一种复杂的固有性质,很容易理解,但并不容易标定.最初,人们使用体弹模量B[5]或剪切弹模量G[40]来标度硬度,但不能完整地表达硬度的含义[41].硬度可以定义为材料局部抵抗硬物压入其表面的能力,也可以表示成物体抵抗外力破坏的能力.硬度的标度方式主要有三种:1)划痕硬度,如在18世纪已经提出、19世纪规范为莫氏硬度的硬度计量方法,其在天然宝石、矿物硬度标度中依然广泛使用;2)压入硬度,包括常用来表示金属硬度的洛氏硬度、机械和冶金工业中常用的布氏硬度、广泛使用的维氏硬度及其延伸显微硬度等;3)回跳硬度,如肖氏硬度.
1921年,维克斯公司的Smith和Sand land[42]提出了维氏硬度,该公司试制了第一台以此方法进行试验的硬度计.维氏硬度的优点在于适用范围广,既适用于超硬物质也可以用于很软的物质,因此它是超硬材料领域经常使用的一种硬度,广泛用于超硬材料合成和设计研究中.维氏硬度的定义是压力除以压痕面积乘一个比例系数,从其定义上它的单位与压强具有相同的量纲,常用的单位有kg/mm2和GPa两个单位,这使得硬度与压强产生了密不可分的联系.硬度无论是在定义的形式、单位都和压强存在某种密切联系,高压是合成超硬材料最有效的方法,这从一开始就决定了硬度与高压是密不可分的.
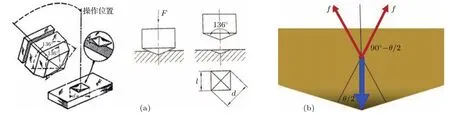
图1 (a)维氏硬度测量金刚石压锥与压痕示意图;(b)压头/物体受力分析Fig.1.(a)Schematic d iagramof d iamond indenter and indentation of V ickers hardness measu rement;(b)force analysis of the indenter and the sample.
如图1所示,测量用压头是一个四棱锥,因此压头所受的力可以分解为四个与中轴成一定夹角的力,压头压入样品表面会在表面留下一个倒置四棱锥状的压坑,当最终形成压痕时,施加的载荷与压痕表面对样品支撑的力达到平衡,如果假设压痕表面所受的压强值均匀,其在压痕表面的压强与测量得到的硬度值基本相同.另外,作用在每个三角形面上的力可以分解为两个方向:第一个方向f1垂直向下,即对样品的压缩;另一个力f2对应于对样品的侧向推力,产生一个强的剪切力.本测试可以很好地体现物体的抗压缩和剪切能力.维氏硬度定义如下:
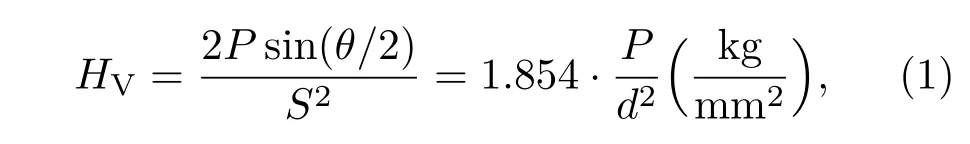
其中,P为载荷;d为压痕对角线长度(mm);S为压痕表面积;θ为四棱锥压头两相对面间夹角,θ=136◦.
硬度测试过程仍然存在着一些令人难以理解的问题,比如随着硬度测试时所施加的载荷力的增加,所测得的样品硬度值在逐渐减小,即硬度尺寸效应,人们也常常通过弹性形变量与塑性形变量的大小来解释硬度压痕效应,认为在低载荷下硬度测试完成时撤去压头的瞬间压痕发生了一定量的弹性形变,使得压痕面积变小,因此在低载荷下的硬度值比较高.但是,单位面积上压痕所受的力是否完全相同,甚至在低载荷下单位面积上压痕所受的力更大,反而发生了一定的弹性恢复,这是比较反常的,因此硬度压痕尺寸效应应该另有深层次的原因.另外通过对比还可以发现不同物质发生弹性形变的力的区间,即非线性区的宽度也大不相同,且其从弹性区至塑性区硬度值的相对坍塌量也有很大的不同.另外物质内部的缺陷、掺杂、晶粒大小、晶界分布、样品致密度等都会对物质的硬度产生影响.即便经过了几百年的探索,硬度在基本定义和测量上还存在很多问题.
2.2 硬度模型
从微观出发解决宏观现象,一直是物理学家努力的一个方向.对于宏观硬度的微观机制经过了长期深入的探究,已经取得了较大进展并提出了一些硬度模型,很好地解决了一些典型物质的硬度问题.
早期的硬度理论主要关注硬度与材料的弹性模量B与G之间的关系,进而形成了一系列的弹性模型.近十年,人们发现硬度不仅仅与弹性形变有关,而是一个与弹性和塑性形变均有联系的量,所以逐渐开始关注材料的微观结构、化学键、电子结构等物理量与材料的硬度值之间的关系,先后建立了相关的硬度模型.
20世纪50年代,Gilman[43],Liu和Cohen[5]发现硬度值较高的材料均具有较高的体弹模量B,最初人们建立了硬度值与体弹模量之间的关系,但是之后的实践中发现体弹模量B与硬度值之间的关系并不大.1996年,Teter和Hemley[44]又发现材料的硬度值与材料的剪切模量G之间有一定的正比关系,HV=0.151G.该经验公式为寻找高硬度材料提供了一个清晰简单的思路,虽然硬度与弹性常数之间的关系有较大的误差,高的体弹模量和剪切模量依然是人们寻找高硬度材料最基本的一个标准.随着第一性原理计算的发展,人们可以用更本质的微观物理量来定量地描述硬度,估算材料的硬度值.
压痕测试时,如果忽略晶界等其他因素,硬度即是样品表面变形区域所有化学键对金刚石压头的总的反作用力,也就是硬度正比于化学键的强度与化学键密度的乘积.化学键的密度越高,键强越强,则材料的硬度值将会随之提高.基于此基本概念,人们提出了众多的硬度模型,但依然是通过不同的晶体物理参量定义晶体当中化学键的强度,从而根据所定义的键的强度及类型计算材料的硬度.
2003年,根据压痕测试的原理,针对共价化合物以及极性共价化合物,燕山大学高发明[45]提出一种基于共价键和极性共价键断裂的硬度模型.硬度公式为
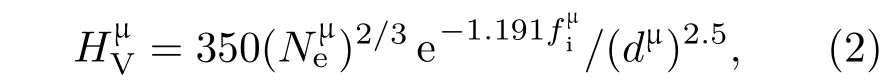
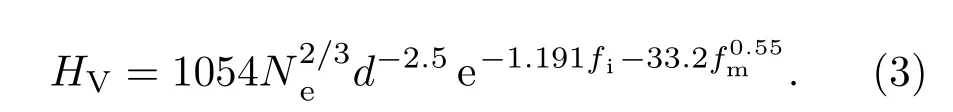
从以上模型可以看出:越高的键密度/电子密度、越短的化学键、越纯粹的共价键、越低的金属性与离子性、越强的s—p或s—p—d键等因素都有利于提升物质的硬度.但是,以上模型也存在一些不足,如:化学键强度与离子性依然缺乏明确定义,未考虑物质的空间结构等因素.
2006年,捷克科学院的Šimůnek和Vackář[48]假设硬度值正比于化学键的强度和化学键的密度,以静电作用定义了键强参量Sij,并引入了离子性修正参数fe,最终得到硬度公式

2.3 设计的基本思想及方法
超硬物质体系内部原子在压力作用下保持相对位置不变,体系中的原子不容易产生错位.超硬材料有类似的特性:1)材料是各向同性的,微观上看材料的晶体结构有高对称性;2)高价电子密度,在外加压力下体系更容易产生内部应力;3)体系内部有方向性很强的共价键网络或强度高且有方向的离子键,这样可以防止体系内原子产生脱位,金属键和离子键通常没有方向性,所以对生成超硬材料不利[26,27].从硬度模型可以看到,为获得过渡金属与轻元素超硬材料,化合物内部应该具有尽量高的键密度和电子密度,并应该尽量减少物质内部的离子键与金属键的成分.这些原则也为寻找、设计超硬材料提供了一定的依据和方向.
材料是有一定功能的物质,确定一个材料不仅仅需要知道材料的组分,同时需要知道材料的结构.半径较小的原子掺入到半径较大的原子体系,小原子的存在可以防止较大原子发生移位,从而提高整体硬度,这个传统方法在制备和设计更硬的材料中广泛使用[26].图2[25]给出了物质结合能及体弹性模量的自然对数随原子序数变化的规律,我们会发现两个量随原子序数变化遵循着相似的规律,两个量都可以反映出物质内部价电子的浓度,可以发现在轻元素区和过渡金属区存在着若干“高价电子密度元素岛”.过渡金属很高的价电子密度和体弹性模量,为产生超硬材料提供了有利条件,但是由于金属键的特性,过渡金属的剪切弹性模量往往不高,所以不能成为超硬材料.p电子轻元素硼、碳、氮、氧也有很高的电子密度.二者形成化合物体系依然会继承高价电子密度这一特性,确保了化合物有很高的体弹性模量;同时,这些p电子原子本身可以形成共价键网络骨架,也可以与过渡金属形成共价键或有一定方向性的离子键,可以阻止原子发生移位,提高材料的剪切模量,这是寻找超硬材料的一个重要方向[25−27].过渡金属的d,f轨道电子性质复杂,尤其是在高密度/高压力的情况下,含过渡金属的物质会有很多奇特性质.可以预见,高压下过渡金属化合物组成原子中的p,d,f轨道的相互作用会与常压下的表现大为不同,将带来大量的新的物理现象,从而对认识压力对物质的作用有很多新的启发,也会产生很多意想不到的性能和性质.

确定材料的性能必须知道物质的结构.物质的结构可以通过X光衍射、中子散射等方法确定,但是对于可能大量存在的新型材料的结构,由理论进行设计和筛选显然成本更低、更便捷;另外,对于过渡金属与轻元素化合物,通常由于过渡金属元素的反射因子远大于轻元素,对于一些不同组分的物质,X光实验无法将它们区分开,这也是实验研究遇到的一个困难[50].超硬材料往往是以亚稳相形式保存到常压的高压稳定相,寻找高压相是发现高硬度新型材料的可靠手段.对一些电子结构近似的物质可以应用结构数据库[51]提供的结构、或者文献报道的新的高压结构进行元素替代以确定新物质的候选结构[52].但是,由于不同元素毕竟存在着差别,即便常规条件下性质非常相近,在压力作用下其表现也可能有很大差别.如,Fe和Cr在元素周期表中位置接近,很多物理性质相仿,但是在压力作用下,FeB4和CrB4却有不同的相变规律[53].同时,从数据库中选择的可能结构也有限,而且未必是同等条件下热力学的最优结构,这就需要一些算法来寻找物质在特定条件下的可能结构.
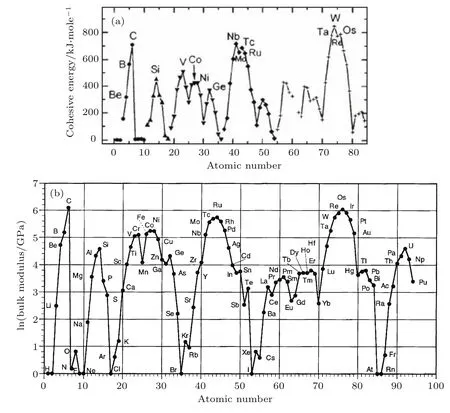
图2 (a)原子序数和结合能的关系[41];(b)体弹性模量的自然对数和原子系数的关系[26].两个性质随着原子系数的演化都遵循着近似的规则[41]Fig.2.(a)Cohesive energy as a function of atomic number[41];(b)natu ral logarithmof the bu lk modu lus as a function of atomic number[26].Both properties followsimilar trends within the period ic tab le[41].
能量是考虑物质结构的重要判据,通常认为低温物质的结构对应于能量全局最小值,即以物质内粒子坐标为变量的物质总能量函数的最小值;局域最小值,也就是能量平面上的某些鞍点,在特定的情况下也可以存在,由于现在依然无法准确判断鞍点周围势垒的高度,很难估计这些局域最小值对应的结构的热力学稳定性.物质的能量如(6)式所示,
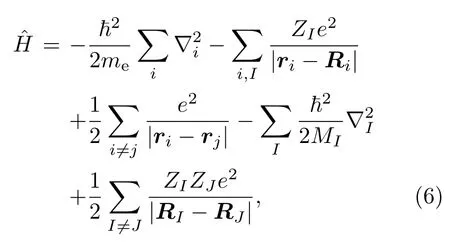
其中ZI和MI分别代表RI处原子实的核电荷数和质量,me为电子质量,ri为第i个电子所在位置,物质的总能量可以看作变量RI和ri的函数.由于电子一般不会远离原子实,所以可以简单地把物质的能量看成原子实占位的函数,由数学知识,这样的函数有3N!个极小值,当体系中的粒子数达到一定数目找到其中最小值基本上是不可能的,这需要一定的数学算法来解决.随着如 USPEX[54,55],CALYPSO[56−58],Minima Hopping[59],AIRSS[60],MAISE[61]等结构预测软件的成熟,找到有更好性质的新结构不仅成为可能,而且随着各种结构搜索软件的完善,找寻过程变得成本更低、效率更高.通过对其在特定条件下的热力学稳定性、动力学稳定性以及力学稳定性进行检验,可以确定所得到的结构是否合理.
近年来,随着密度泛函理论方法的发展和计算机技术的提高,凝聚态体系的第一性原理计算能力得到了空前的发展.利用第一性原理方法来计算物质力学、热学、光学、电磁学性质已经达到了相当的精确程度.一旦确定一种物质的组分、结构和存在条件,就可以对其性质进行研究,获得非常准确的数据.
3 过渡金属轻元素化合物功能材料的设计
过渡金属轻元素化合物的研究主要集中在过渡金属硼、碳、氮、氧化合物,通过对高压相的探索来寻找新型的超硬(硬质)多功能材料是广泛应用的手段.过渡金属轻质元素化合物的性质随轻元素比例变化往往呈现出一些规律性特征,这在过渡金属氮化物中有较为突出的表现.
氮化物由于N独特的从三键转化为单键的键合变化,可以形成空间网络,这在单质氮[62,63]和含氮化合物[64−68]中都大量理论预言和发现.如铼氮化合物的研究中[69]很好地表现出氮浓度驱动铼-氮化合物的硬度及其他性质的变化.作者探索了多种化学配比可能的Re-N化合物,应用结构搜索方法和第一性原理计算探究了Re-N化合物的零温高压相图,如图3所示.提出了稳定的Re/N化学计量配比Re3N2和ReN3材料,更新了先前理论预测的ReN4高压结构,如图4所示.计算材料的弹性常数和声子谱,证明Re-N化合物例如ReN2和ReN3可以通过高压合成,并恢复到常压条件.由图4可以发现,随着氮含量的增加,Re-N化合物的结构由层状排列结构转化为3D多面体堆叠结构.晶体结构由Re-N-Re层状构型转变为ReNx多面体堆砌结构,富氮Re-N化合物结构中的多面体堆砌结构可以有效避免Re—Re金属键的相互作用,是形成超硬材料的必要条件.N—N双氮单元、N—N—N三氮单元以及Nn链出现在富氮材料中,N—N键长接近1.40Å,为单键.众所周知,N≡N到N—N伴随着很大的能量变化,是以氮为基础的高能化合物的储能基础,但是由于过渡金属元素质量比较高,所以过渡金属氮化合物通常无法作为高能量密度材料,但是否可以作为一种潜在的储能材料仍有待研究.进一步对力学性质的研究中发现,Re-N化合物的剪切模量随氮含量的增加显著提升,泊松比显著降低,硬度得到了显著的提升[69].进一步分析电子结构发现高的N含量可以促进p电子参与成键,形成强共价性的3D多面体堆叠结构,从而有效地限制材料中Re—Re金属键数量以及Re—N键的金属性.计算得到富氮的ReN2和ReN3材料的理论硬度可以分别达到38GPa和44GPa,是潜在的超硬材料.由图5可以看到:随着氮含量增大,体弹模量和密度降低,这说明结构的不可压缩性和价电子浓度降低;剪切模量和杨氏模量增大,泊松比显著降低,说明材料的共价性增强,硬度增大;ReN2,ReN3,ReN4结构G和E的均值对比富Re相提升了大约50和90 GPa,泊松比由典型的金属的值降低为共价材料的值.进一步对Re-N材料的电子态密度进行研究,从图6可以看到随着氮含量的增加,Re-N化合物的金属性显著降低,逐渐出现了带隙的趋势,ReN3具有最小的费米能级处态密度(DOS)值,金属性非常弱.ReN4已经接近绝缘体了;Re的d电子和N的2p电子的杂化效应随着氮含量的增加显著变强,尤其在−5到0 eV之间的能量范围,说明随着氮含量的提升,有更多的p电子参与Re—N成键,因此提升了材料的硬度.这些结果证明氮含量是影响Re-N化合物硬度的关键因素.其中ReN4常压下的硬度可能达到38.7 GPa.在Ru-N体系[70]、Ta-N体系[71]中也表现出了类似的规律.

图3 Re-N体系的高压相图及各相稳定区间[69]Fig.3.Compu tational phase orders of nitrogen,respectively.Red lines represent newphases proposed in thiswork.N-rich stoichiometries are high lighted by cyan shadows[69].
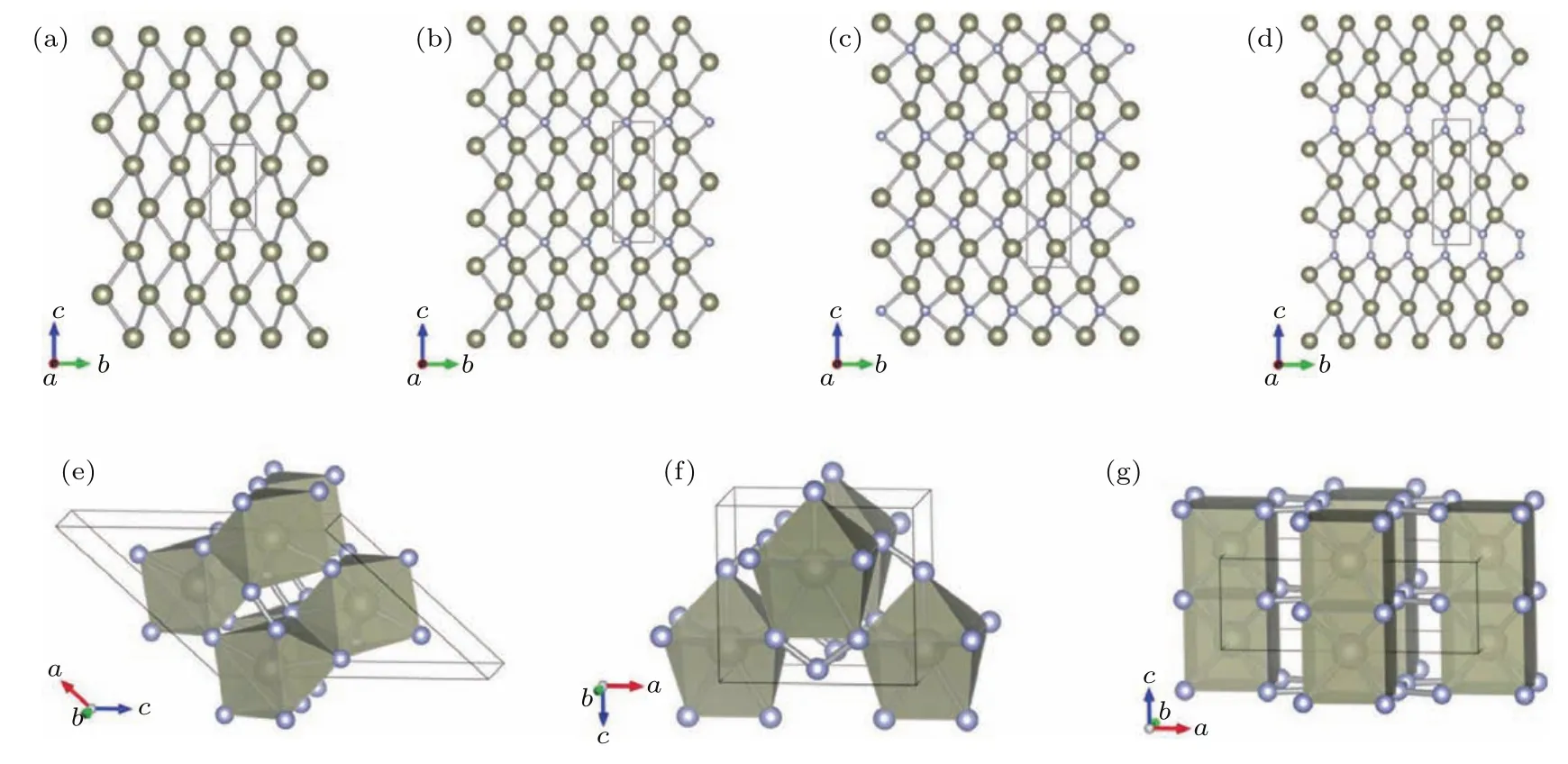
图4 Re-N化合物的晶体结构 (a)Re;(b)Re3N;(c)Re2N;(d)Re3N2;(e)ReN2;(f)ReN3;(g)ReN4;大球代表Re原子,小球代表N原子[69]Fig.4.The structures of Rheniumnitrides:(a)Re;(b)Re3N;(c)Re2N;(d)Re3N2;(e)ReN2;(f)ReN3;(g)ReN4.The big and small spheres present the rheniumand nitrogen atoms respectively[69].
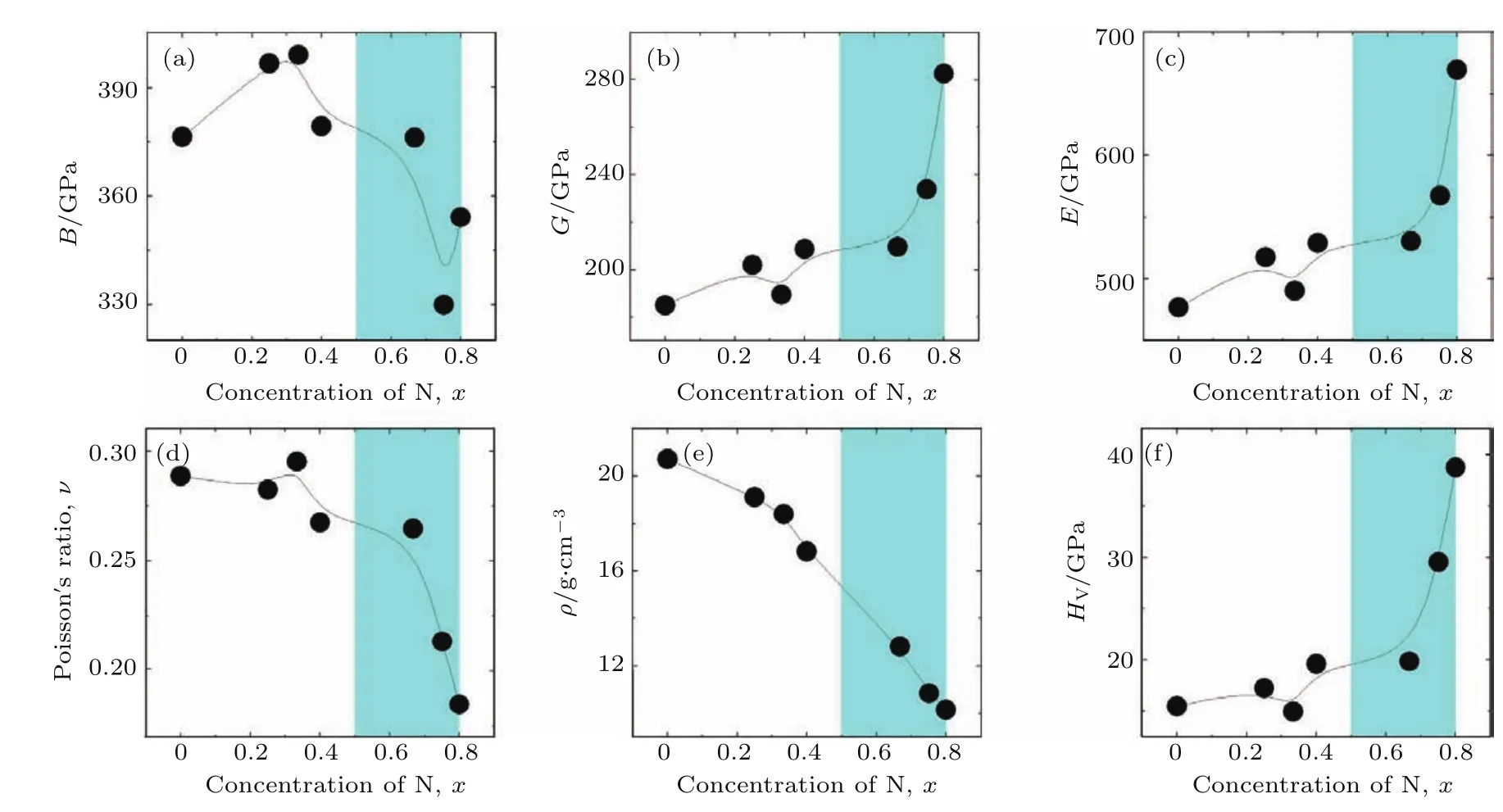
图5 Re-N化合物常压下的弹性性质和硬度随氮含量的变化[69](a)体弹模量;(b)剪切模量;(c)杨氏模量;(d)泊松比;(e)体密度;(f)维氏硬度Fig.5.Changes ofmechanicalpropertieswith the concentration of nitrogen of Re-N’s[69]:(a)Bu lkmodu lus;(b)shear modu lus;(c)Young’smodu lus;(d)Poisson’s ratio;(e)density;(f)V icker’s hardness.
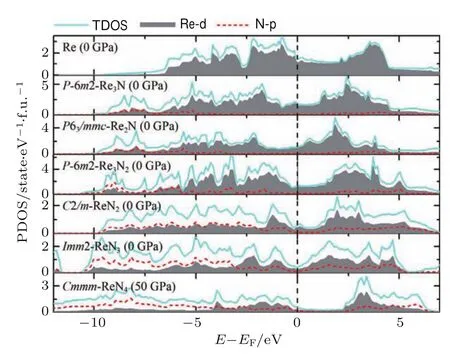
图6 Re-N化合物的电子态密度随N浓度变化的规律[69]Fig.6.Calcu lated total density of states(TDOS)and partial density of states(PDOS)of Re nitrides at diff erent pressu res.The vertical dash line at zerois the Fermi energy level[69].
近期对铬-氮体系的研究中发现CrN2可能为一种半导体,六方密堆结构的CrN2通过高压与N-N预压联合作用,合成压力可以在比较温和的7 GPa左右,处在传统六面顶压机能够提供的压力范围内,而它的理论硬度达到46 GPa[72].作者通过第一性原理模拟结合多种形式的交换关联泛函(Perdew-Burke-Ernzerhof(PBE)、局域密度近似(LDA+U)、Heyd-Scuseria-Ernzerhof(HSE)杂化泛函等)、晶体结构预测USPEX方法以及第一性原理分子动力学模拟,预测具有hcp结构的CrN化合物可以在超高压力下合成,见图7.通过将hcp结构的CrN化合物中的氮原子替换成N-N单元,证明hcp结构CrN2可以在小于10 GPa的相对较低的压力下稳定.通过计算材料的电子局域函数,发现了上述hcp结构的Cr-N化合物稳定压力的降低来自于填隙N-N单元的预压缩作用,见图8.在N-N预压缩的作用下,材料中Cr—N化学键键长显著缩短,电子的局域性显著增强,对材料起到了一种预先添加化学压力的作用,从而将材料的稳定压力由108GPa降低到7GPa.Cr-N体系的电子态密度见图9.由于电子的局域效果,材料的共价键显著增强,大大提升了材料的硬度.此外,发现在N-N预压缩的作用下,hcp结构Cr-N化合物由金属转变为绝缘体.这种金属绝缘体转变来自于N-N单元对Cr金属层中传导电子的屏蔽作用,是一种新奇的金属绝缘体转变现象.此工作突出了聚合的氮单元对于过渡金属氮化物电子结构、硬度以及合成条件的影响.半导体性的过渡金属化合物出现,说明了系统中严重影响硬度的金属键成分被抑制,材料硬度得以大幅提升.

图7 (a)CrN化合物焓差-压力曲线;(b)C rN2化合物的形成焓-压力曲线;(c)Cr-N体系高压下的热力学凸包曲线图[72]Fig.7.Calcu lated(a)enthalpy diff erence vs pressu re(Hdiff-P)cu rves of C rN,(b)formation enthalpy vs pressure(Hform-P)curves of C rN2,and(c)the convex hu ll d iagramof C r-N systemat 10 GPa with LDA+Umethod[72].
硼和氮成键规律有类似的地方,硼化物是过渡金属化合物中被研究得最多的.一方面,由于硼成键的性质使得硼拥有复杂的基本结构[73−75],所以硼容易形成复杂共价键网络;另一方面,过渡金属硼化物的合成相对简单,理论预测的结论和实验测量的结果容易进行比较.
从含硼量上来看,近期内发现了一大批TMB12类化合物,并有大量的理论和实验研究[76−80],它们的结构如图10所示,可以看成是B的十四面体内放入过渡金属原子,这一系列是目前研究中含硼量最高的结构.目前得到的过渡金属硼十二化合物的硬度虽然不到超硬材料的标准,依然比较高,但低于同类元素的二硼化物.实验测量ZrB12的电阻率为18µΩ.cm,其中共价键硼网络结构不仅作为骨骼,使材料具有较高的硬度,而且充当了非常好的电子通道[78].由于硼成键的特殊性,可能会存在更多高对称性硼笼中填充过渡金属元素的结构,有待更多的研究发现.
硼化物的结构演化也显示一定的规律性,见图11,但并没有过渡金属氮化物那样显著.过渡金属硼化物有丰富的相图,同一化学配比可能存在多种稳定结构,如在铌-硼化合物的研究中[81],除了最稳定的单斜C 2/c结构的NbB3,还可以存在四种亚稳态结构P 63/mmm,C 2/m,Pmm2和I¯4m2,这5种结构都可以存在于常压条件下.从对Ti-B[82]和Hf-B[83]体系的研究中,可以看到化学
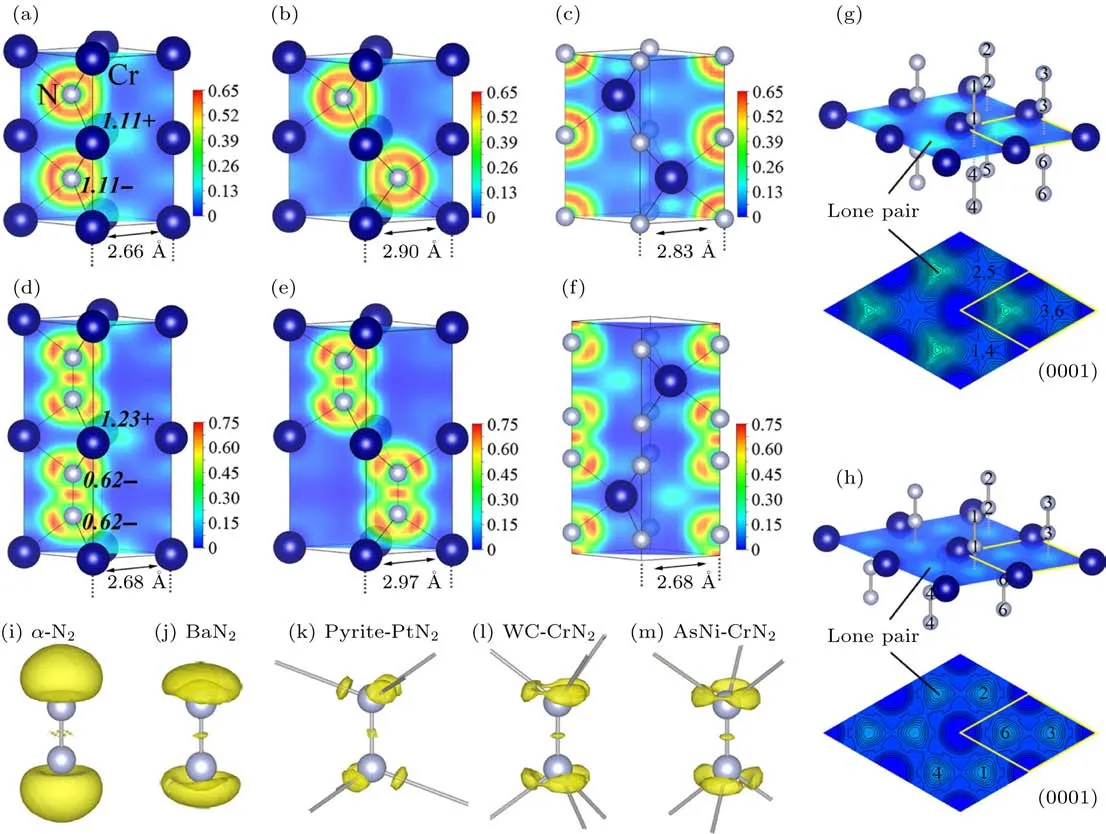
图8 0压下的物质结构与电子局域函数[72](a)WC-CrN;(b)NiAs-CrN;(c)AsNi-CrN;(d)WC-CrN2;(e)NiAs-CrN2;(f)AsNi-CrN2;(g)WC-CrN2的(0001)平面;(h)N iAs-CrN2的(0001)平面;(i)分子氮;(j)BaN2中的N=N;(k)PtN2中的N—N;(l)WC-C rN2中的N—N;(m)AsN i-C rN2中的N—NFig.8.Crystal structu res and electron localization functions(ELFs)of(a)W C-CrN,(b)N iAs-CrN,(c)AsNi-CrN,(d)W CC rN2,(e)NiAs-C rN2,and(f)AsN i-C rN2with the scales running from0(b lue)tomaximum(red).Bader charges(bold italics)and cell parameter a are indicated.The calcu lated(0001)plane ELFs ofWC-CrN2and N iAs-CrN2are showed in(g)and(h)with the same scales.The th ree-d imensional bonding topologies of(i)N≡N triple bond inα-N2,(j)N=N doub le bond in BaN2,and(k)N—N single bond in pyrite-PtN2are showed with an isosurface at ELF=0.85.The N—N single bonding pictu res ofWC-C rN2and AsNi-CrN2are shown in(l)and(m)with the same level.Data in(a)–(h)are calcu lated with LDA+U,while in(i)–(m)they are achieved with PBE for comparability.All data are calcu lated at 0 GPa[72].

图9 0 GPa下六角铬-氮化合物由PBE型交换关联泛函和LDA+U方法计算的电子态密度,其中垂直虚线表示费米能级;采用LDA+U能量修正计算的WC型C rN的电子自旋劈裂用阴影表示[72]Fig.9.E lectronic density of states of proposed hexagonal C r nitrides at 0 GPa calcu lated with PBE and LDA+Umethods.The vertical dashed lines indicate the Fermi levels.The LDA+Uenergy corrections for the spin splitting of WC-CrN are depicted in the b lack shadow[72].
配比对硬度有更重要的影响,通过对不同过渡金属硼化物的比较[76,81−90],过渡金属的选择对材料硬度的影响大于结构的作用,一般TMB12[76−80]的硬度由于硼框架的存在普遍比较高,但是在实际计算中,需要仔细选择过渡金属原子,并不是任意过渡金属元素处于笼中,笼子都能保持稳定,过渡金属与硼笼之间的相互作用需要进一步研究.
图12中列出了几种目前报道的硬度比较高的硼化物,可以看出物质的对称性、化学比甚至电子态密度等方面都没有明显的规律,寻求过渡金属硼化物设计的一般性、规律性的指导还为时尚早.更多硼化物的对称性、力学性质和硬度可以参考附录A.不过一般而言,高硬度硼化物的费米面处态密度并不高,处在态密度曲线的鞍点或附近.以目前的研究状况来看,很难找到一个合理性的数值判据.硼的空间网络可能同时兼具着材料硬度骨架和电子通道的双重作用.高硬度过渡金属硼化物的设计,对过渡金属的选择十分重要,总体看来原子半径比较小,价电子浓度较高的过渡金属原子更容易形成硬度比较高的过渡金属硼化物.
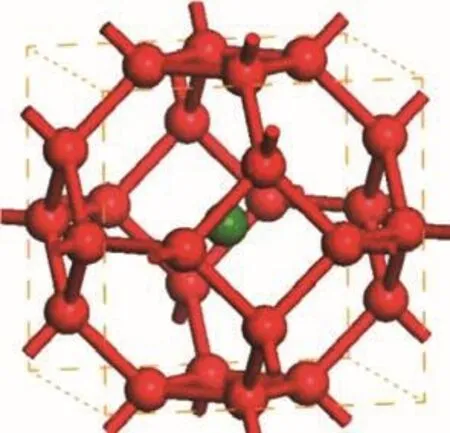
图10 十四面体示意图,红色代表B原子,绿色代表过渡金属原子Fig.10.Illusion of a tetrakaidecahed ron,red balls present Boron,an the green ball presents a transition metal atom.

图11 (a)有两个不等价硼的包含共轭硼环或者双连接的锯齿状硼链的P 21/m结构M2B3(M=Co,Rh和Ir);(b)常压下CoB2的晶体结构;(c)常压下RhB2的晶体结构;(d)常压下IrB2的晶体结构;(e)常压下Ir4B5的晶体结构;绿色球代表硼原子,蓝色、紫色以及红色球代表各种金属原子[90]Fig.11.(a)Crystal structu re of the P 21/m-type M2B3(M=Co,Rh,and Ir);crystal structu res for(b)CoB2,(c)RhB2,(d)IrB2,and(e)IrB1.25(Ir4B5)at ambient pressu re.G reen spheres represent Batoms;b lue,purple,and red spheres representmetal atoms[90].
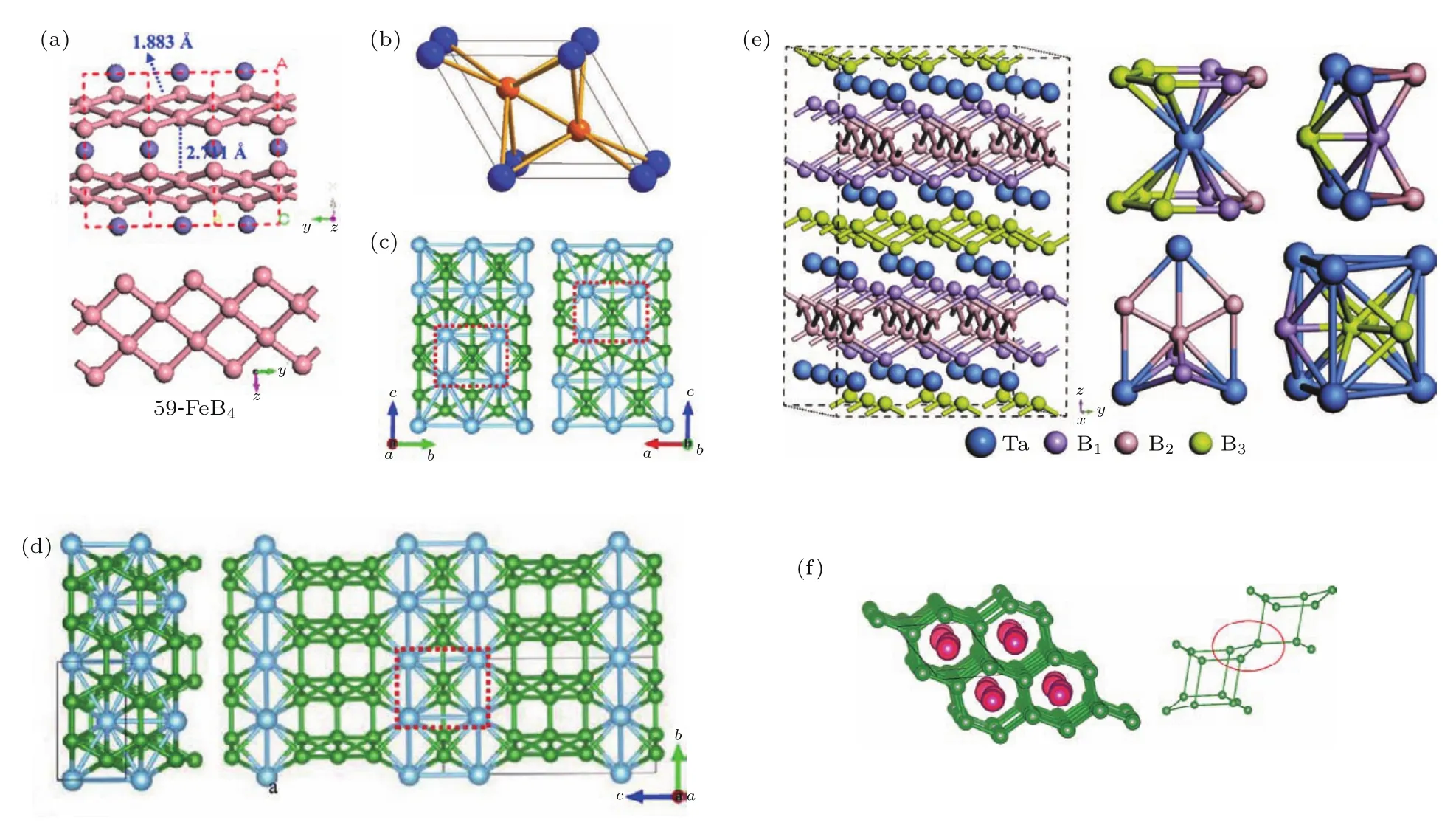
图12(a)Pmmn-FeB4的结构图,理论硬度为48.1GPa,蓝色小球为铁原子,粉色小球为硼原子[89];(b)P 6/mmm-VB2的结构图,理论硬度为53.4 GPa,蓝色小球为钒原子,橙色小球为硼原子[93];(c)P 42/mmc 267-TiB2的结构图,理论硬度为39.6 GPa,银色小球代表钛原子,绿色小球代表硼原子[82];(d)Amm2-TiB4的结构图,理论硬度为38.2 GPa,银色小球代表钛原子,绿色小球代表硼原子[82];(e)Imma-TaB3的结构图,理论硬度为41 GPa,大球和小球分别代表钽和硼原子,不同颜色的硼代表不同的W yckoff占位,详见原文[84];(f)C 2/m-NbB3,理论硬度为44.3 GPa,红色小球代表铌原子,绿色小球代表硼原子[81]Fig.12.(a)Structu re of Pmmn-FeB4,the theoretical hardness is 48.1 GPa,the b lue balls present iron atoms,and the pink ones are boron[89];(b)structure of P 6/mmm-VB2,the theoretical hardness is 53.4 GPa,the b lue and orange balls present V and Batoms[93];(c)structu re of P 42/mmc-TiB2,the theoretical hardness is 39.6 GPa the silver and b lue balls present Tiand Batoms[82];(d)structure of Amm2-TiB4,the theoretical hardness is 38.2 GPa,the silver and b lue balls present Ti and Batoms[82];(e)crystal structu re and the nearest coordination number of tantalumand boron atoms inImma-TaB3,the theoreticalhardness is 41GPa.The large and small spheres represent tantalumand boron atoms,respectively.For boron,diff erent colour spheres represent d iff erent W yckoff sites[84];(f)crystal structu re of C 2/m-NbB3,the theoretical hardness is 44.3 GPa,the red and green balls repesents the Ni and Batoms[81].
对过渡金属碳化物的研究相对较少,已有的报道中Cmmm结构的OsC4的硬度为37 GPa[91],F¯43m/216结构RuC的硬度为36.66 GPa[92],TcC的研究中发现WC型TcC(Fm2)的硬度可以达到26 GPa[93],NiAs型TcC(P 63mc)的硬度可以达到25 GPa[93,94].虽然没有达到超硬材料40 GPa的标准,但已经达到了常用硬物质,如碳化钨(26.4 GPa)和刚玉(20.6 GPa)的硬度水平.以上文章都认为C的2p电子与过渡金属的d电子产生了杂化作用,过渡金属原子与碳原子之间由于杂化形成了比较强的方向性共价键,从而大大提升了物质的硬度.在对其他过渡金属轻元素化合物的研究中类似的讨论虽不多见,但这是一个值得注意的思考方向.
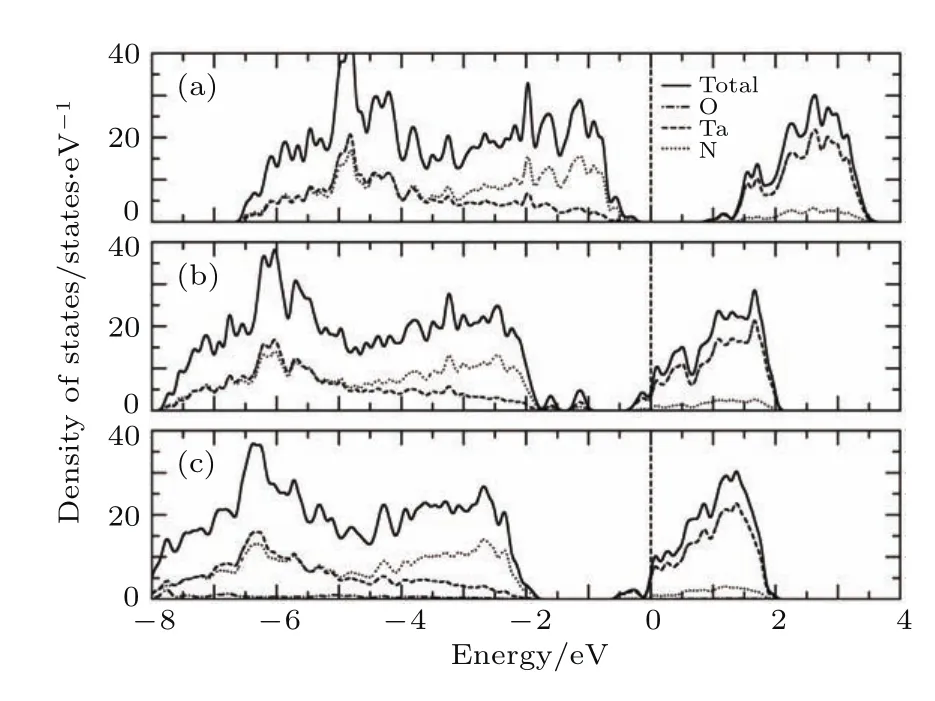
图13 (a)纯Ta3N5的电子态密度;(b)存在N空位的Ta3N5的电子态密度;(c)氧掺杂的Ta3N5的电子态密度[95]Fig.13.Calcu lated densities of states:(a)Pu re Ta3N5,(b)Ta3N5with N vacancies;(c)Ta3N5with Osubstitution.The Fermi level is at zero[95].
掺杂一直是调制物质性能的一种重要方法,Cui等[95]对存在氮缺失和氧取代的Ta3N5进行了研究,发现氧替代不仅可以增加Ta3N5的稳定性,同时Ta3N5还具有半导体性质,其电子结构见图13.虽然文章没有给出硬度,但由图13可见O掺杂的Ta3N5是半导体.一般情况下,由于金属键的消失,过渡金属化合物的硬度会大大提高.
4 存在的问题
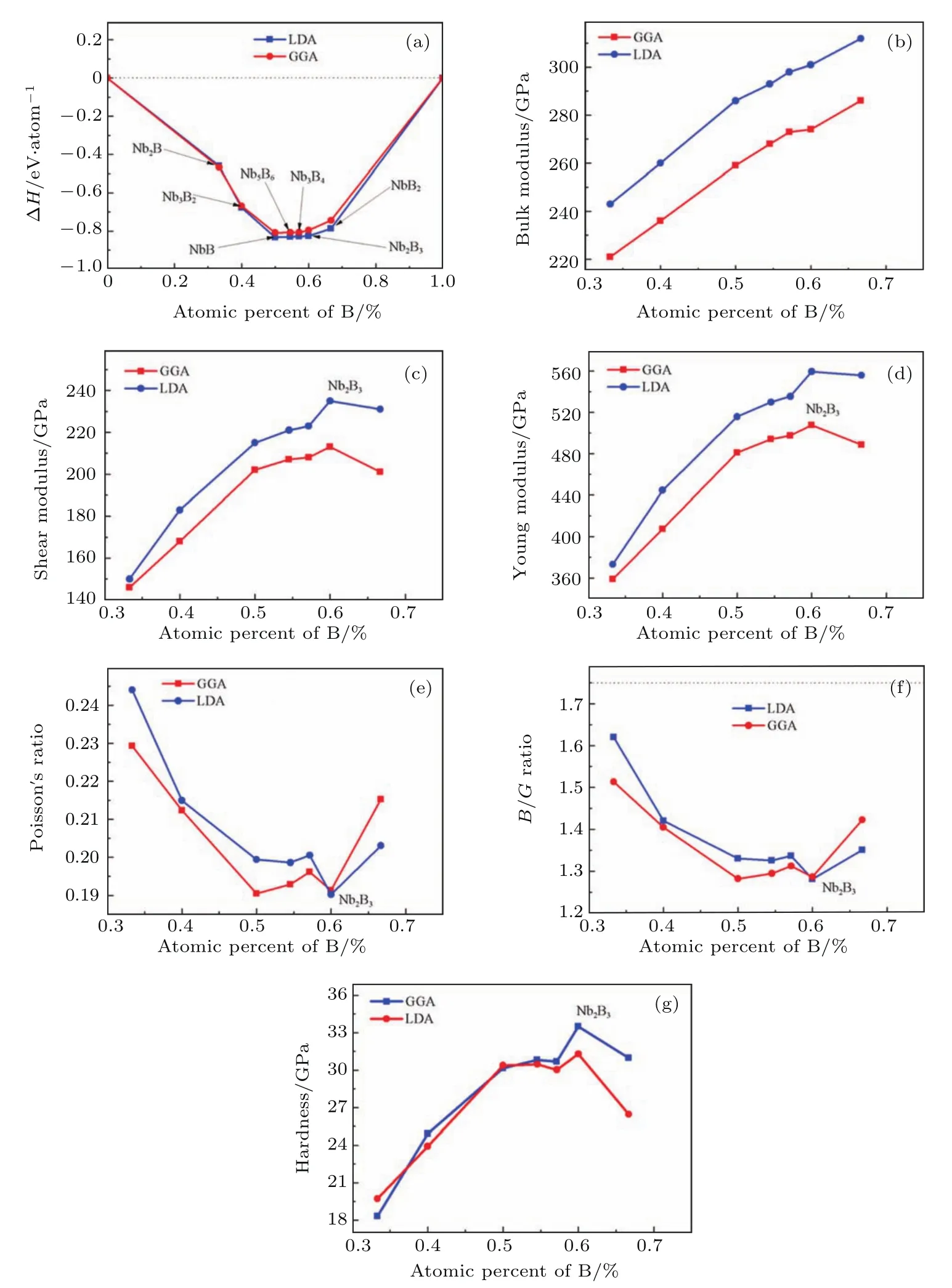
图14 以铌硼体系为例,采用CA型局域密度近似和PBE型广义梯度近似计算系列Nb-B化合物的热力学和力学参数(a)凸包图;(b)体弹模量;(c)剪切模量;(d)杨氏模量;(e)泊松比;(f)体弹模量比剪切模量;(g)维氏硬度[96]Fig.14.Comparationsof the resu ltsby LDAand GGAasa function of Bconcentration in Nb-N:(a)Enthalpy convex hull;(b)bu lk modu lus;(c)shear modu lus;(d)Young’s modu lus;(e)Poisson’s ratio;(f)B/G ratio;(g)Vickers’hardness[96].
对材料性质的计算受到以密度泛函为基础的第一性原理计算固有缺陷的影响.合理准确地处理交换关联能,一直是密度泛函方法的一个问题,在选择不同关联泛函时,会出现一定的数值差异.如文献[96]中,作者采用CA型局域密度近似和PBE型广义梯度近似计算了系列的铌硼化合物的热力学和力学参数.由图14可见,采用不同交换关联泛函,得到的结果存在一定差异,而且对于特定的情况,体系参量演化规律也会有所差别.同时,由于在压力作用下,原子之间相互作用的状况与平时不同,所以赝势也会有所改变,所用的赝势是否可以准确地描述体系所处的状态也需要仔细考虑;另外,对于较重的过渡金属原子,需要考虑相对论效应;在考虑Fe,Go,Ni,Mn等磁性元素时,如果要取得足够准确的结构,体系的磁结构也需要仔细考虑.物质的电导率、热导率等输运性质的计算,以及磁性、高温超导等宏观量子效应性质的计算,目前还没有非常可靠的计算模拟方法进行准确估算.以上都需要计算物理基本原理、方法及软件进一步发展和完善.
虽然目前已经设计并合成出了大量的过渡金属化合物,但是理论设计和实验可完全相互印证的依然不多.为此Fan等[97]曾经理论上获得了锰-硼化合物P-T理论相图,明确了MnB2理论预言最稳定结构ReB2型MnB2和实验获得的AlB2型MnB2的相边界线,为实验合成高硬度材料提供了重要的温度和压力热力学数据.应用第一性原理的研究中,发现为得到锰-硼化合物的基态,需要仔细设计在合成过程中控制反应温度和压力,对反应路径进行设计和严格控制.理论研究表明,预测的ReB2型MnB2是MnB2的基态结构[98],且是一种潜在的超硬材料.然而,现有的实验无论是高温高压法还是电弧熔融法得到的MnB2只有AlB2型结构[99,100].作者在简谐近似下利用第一性原理晶格动力学计算研究了其压力和温度效应,并确定了ReB2型和AlB2型MnB2的压力温度相边界.发现相边界是一条斜向下的曲线,见图15(b),这说明,ReB2型MnB2在高温高压下热力学不稳定,会转变成AlB2型MnB2.并研究了它们的吉布斯自由能和晶格振动之间的联系,以进一步理解形成这种热力学不稳定性的物理根源.由图15(a)可见,低温下吉布斯自由能中晶格振动贡献部分主要来自于B原子,而高温下Mn原子的振动贡献加强;到900 K以上它主要来自于Mn原子振动的贡献.而在ReB2型MnB2中Mn—B键较短,相互作用较强,它的Mn原子振动频率较AlB2型MnB2要高.因此,高温下虽然其电子能量较低,但它较高的晶格振动能直接导致了它的吉布斯自由能也较高.
该研究结果解释了反应路径与反应条件对过渡金属化合物的生成条件的影响,为实验合成ReB2型MnB2提供了重要的热力学数据,也说明了过渡金属化合物的合成需要对反应条件进行精心设计.理论研究往往采用焓作为物质稳定性的热力学判据,由于现有第一性原理研究手段的限制,无法准确估计每个稳定结构对应局域最小值周边的势垒,从而无法确定亚稳相的热力学存在条件,造成了结构搜索过程中大量有意义的亚稳态结构被忽略.这些因素造成了理论和实验的不一致.

图15 (a)和(b)分别是AlB2型和ReB2型MnB2的声子态密度和声子自由能积分;(c)为AlB2型和ReB2型MnB2的P-T相图[97]Fig.15.PPHDOS and Fphof(a)AlB2-type and(b)ReB2-type MnB2.The b rown dashed line represents the PPHDOS of Mn as a function ofω,and the b lack line is that of B;the pink dot line,green dash dot line,b lue dash double dot line and red short dash line are Fphas a function ofωat 0 K,300 K,600 Kand 900 K,respectively.The percent contribution of the PPHDOS of Band Mn toFphare alsoshown on the left legend.(c)P-Tphase diagramof AlB2-type and ReB2-type MnB2.The red solid and orange dash line represent the calcu lated phase boundaries including and excluding Fel,respectively.The diff erencesofG ibbs free energy(GAlB2(p,T)−GReB2(p,T))between AlB2-type and ReB2-type MnB2are represented by shades fromwhite tob lack[97].
由于过渡金属的X光散射截面远大于轻元素,不同化学组分的过渡金属化合物之间的X光衍射图谱难以区分,造成了实验结果和理论比较的困难.通过各种实验方法合成的W-B化合物是WB3还是WB4一直存在着较大的争论[50,101].另外,由于合成过程中不可避免的元素缺失、晶体成形、晶界特性以及可能混入杂质等原因,也使得实验表征结果和理论结果不一致.通过理论方法的发展及实验合成样品质量的提升、表征手段的完善,最终理论和实验是可以相互印证、互为指导.
5 总 结
理论预言了大量潜在的高硬度过渡金属轻元素化合物,实验上也获得了大量高硬度多功能过渡金属轻质元素化合物,尽管依然缺乏可信的超硬新型过渡金属化合物材料的实验证据,但还是取得了许多有益的结果.目前实验及理论结果找到了很多多功能高硬度材料,解释了很多本质性物理问题.对硬度的理解逐步深入,使得我们可以以硬度的来源为根本出发点,设计新型的高硬度多功能过渡金属轻元素化合物,并给出了合成路径及力学参数.第一性原理计算及物质结构搜索软件的发展,使得确定新型超硬多功能材料变得相对容易,为超硬多功能过渡金属化合物的设计及性质预测提供了有力的武器.在已经提出的材料中N显示出一定规律性,而其他轻质元素情况比较复杂.总体来说,寻找材料的高压相,物质内部形成共价键网络框架、抑制体系内的金属键成分,依然是超硬多功能过渡金属化合物设计的主要思想.在此基础上,应考虑过渡金属的p,d,f电子与轻元素的s,p电子的杂化作用.
过渡金属多功能材料的探索和研究可以说虽然经过了相当长的研究历史,目前已经提出高硬度材料、磁性材料、半导体材料,但仅仅是冰山一角,依然有大量的材料等待获得、很多的技术问题有待突破、深刻的科学问题等待解答.
附录A 一些近期获得的过渡金属硼化物的结构与力学参数和硬度的关系
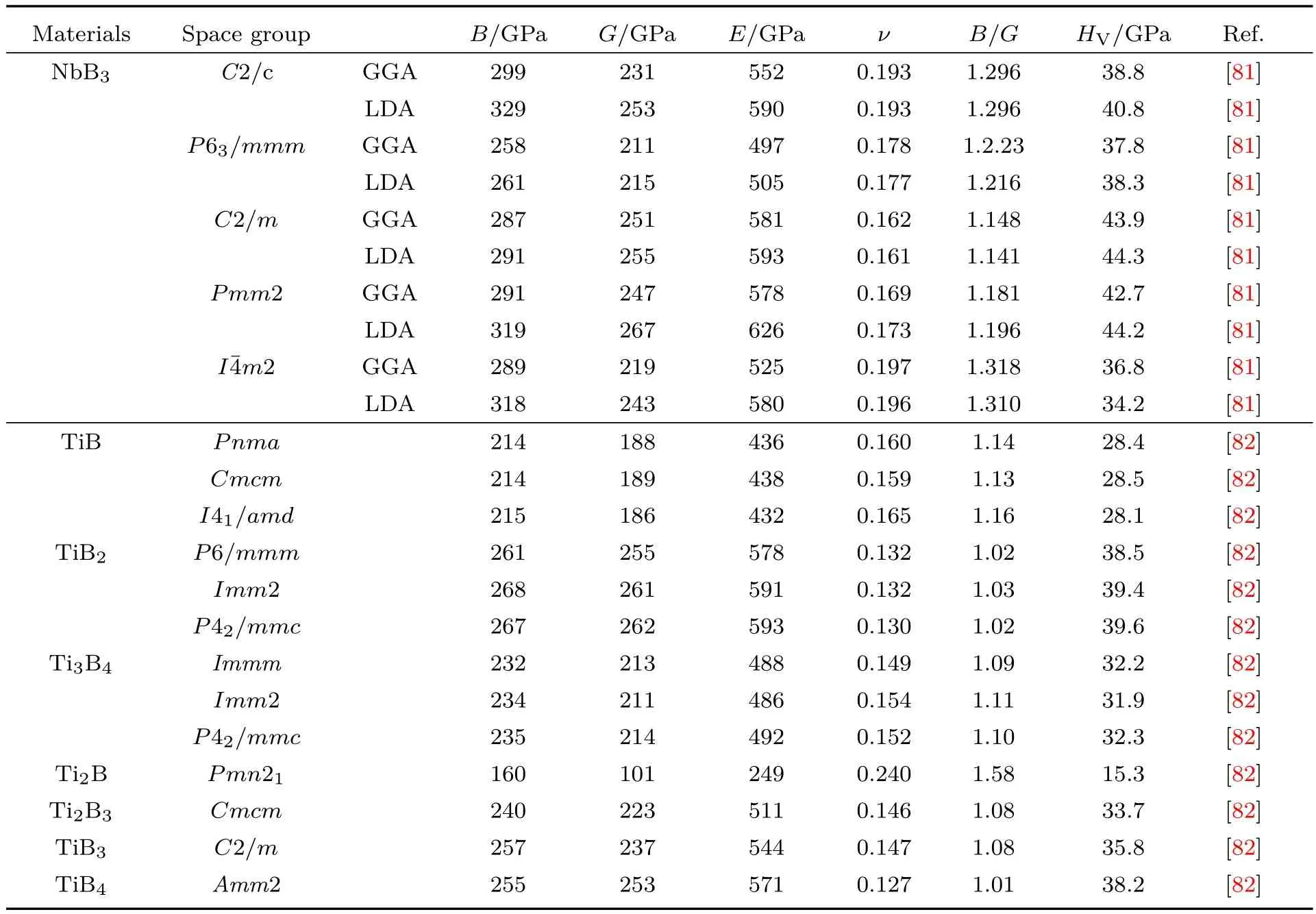
表A1 过渡金属硼化物的体弹性模量B、剪切模量G、杨氏模量E、泊松比ν和维氏硬度HVTab le A1.The bu lk modu lus(B),shearmodu lus(G),Young’smodu lus(E),Poisson’s ratio(ν),and V ickers’hardness of some transition metal borides.
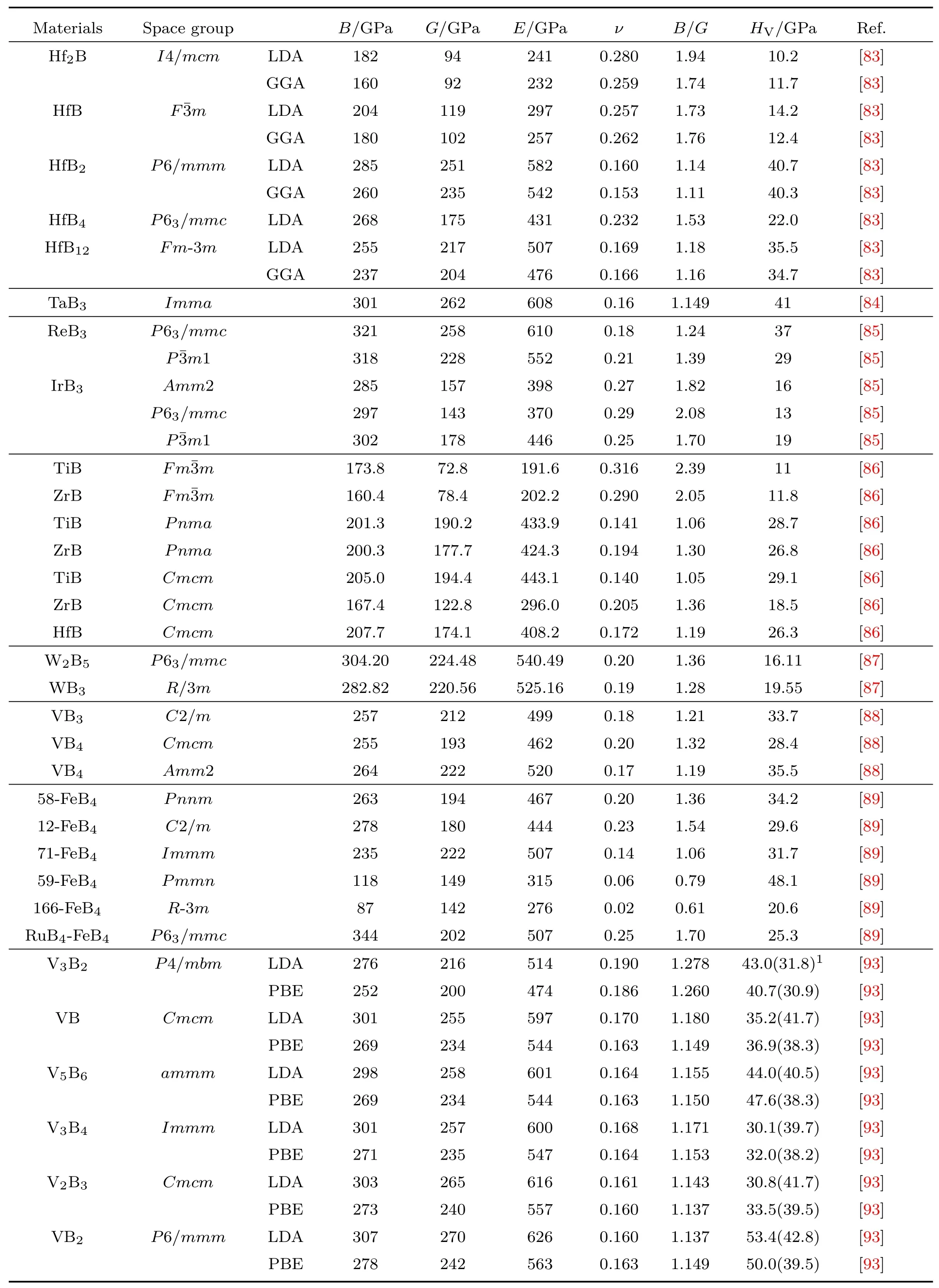
表A1 过渡金属硼化物的体弹性模量B、剪切模量G、杨氏模量E、泊松比ν和维氏硬度HVTab le A1.The bu lk modu lus(B),shearmodu lus(G),Young’smodu lus(E),Poisson’s ratio(ν),and V ickers’hardness of some transition metal borides.
参考文献
[1]Sung C M,Sung M1996Mater.Chem.Phys.43 1
[2]Veprek S 1999J.Vac.Sci.Technol.A17 2401
[3]YooC S,Cynn H,Gygi F,Galli G,Iota V,Nicol M,Carlson S,Husermann D,Mailhiot C 1999Phys.Rev.Lett.83 5527
[4]Li Q,Zheng W T2016Chin.Phys.B25 076103
[5]Liu AY,Cohen ML 1989Science245 841
[6]Li D,Tian F B,Duan D F,ZhaoZ L,Liu Y X,Chu BH,Sha X J,W ang L,Liu BB,Cui T2014RSC Adv.4 17364
[7]X ing MJ,Li BH,Yua Z T,Chen Q 2016RSC Adv.6 32740
[8]MaoW L,MaoHK,Peter J E,Thomas TP,Newville M,KaoC C,Heinz D L,Shu J F,Meng Y,Hemley R J 2003Science302 425
[9]HaoJ,Liu HY,LeiW W,Tang X,Lu J,Liu D,Li Y W 2015J.Phys.Chem.C119 28614
[10]He J L,GuoL C,GuoX J,Liu R P,Tian Y J,Wang HT,GaoC X 2006Appl.Phys.Lett.88 101906
[11]Stav rou E,Lobanov S,Dong HF,Oganov AR,Prakapenka V B,Konôpková Z,Goncharov AF 2016Chem.Mater.28 6925
[12]W ei Q,Zhang MG,Yan HY 2016Phys.Lett.A380 3217
[13]Fan Q Y,Chai C C,W eiQ,Yang Y T2016Materials9 427
[14]Houska J,Steid l P,V lcek J,Martan J 2016Ceram.In t.42 4361
[15]Pan Z C,Sun H,Zhang Y,Chen C F 2009Phys.Rev.Lett.102 055503
[16]He C Y,Sun L Z,Zhang C X,Peng X G,Zhang KW,Zhong J X 2012Phys.Chem.Chem.Phys.14 10967
[17]Huang Q,Yu D L,ZhaoZ S,Fu SW,X iong M,W ang Q Q,GaoY F,LuoK,He J L,Tian Y J 2012J.Appl.Phys.112 053518
[18]W u J H,Liu C X 2016Chin.Phys.Lett.33 036202
[19]Zhang BL 2016J.Alloys Compd.663 862
[20]He D W,ZhaoY S,Daemen L,Qian J,Shen TD,Zerda TW 2002Appl.Phys.Lett.81 643
[21]Q in Y,Shi L W,Zhang S B,Jin F,Zhang L Y,X ia W S,Duan Y F 2016J.Alloys Compd.686 914
[22]W ang S N,Oganov AR,Qian G R,Zhu Q,Dong HF,Dong X,Esfahania MMD 2016Phys.Chem.Chem.Phys.18 1859
[23]Kenichi T2004Phys.Rev.B70 012101
[24]Cynn H,Klepeis J E,YooC S,Young D A2002Phys.Rev.Lett.88 135701
[25]Levine J B,Tolbert S H,Kaner R B2009Adv.Funct.Mater.19 3519
[26]G ilman J J,Chamberland R W,Kaner R B2006In t.J.Refract.Met.Hard Mater.24 1
[27]Kaner R B,Cilman J J,Tolbert S H2005Science308 1268
[28]Chung HY,W einberger MB,Levine J B,Cumberland R W,Kavner A,Yang J M,Tolbert S H,Kaner R B2007Science316 436
[29]Chung HY,W einberger MB,Yang J M,Tolbert S H,Kaner R B2008Appl.Phys.Lett.92 261904
[30]Desgreniers S,Lagarec K1999Phys.Rev.B59 8467
[31]Dubrovinksy L S,Dubrovinskaia N A,Swamy V,Muscat J,Harrison N M,Ahu ja R,HolmB,Johansson B2001Nature410 653
[32]ZhaoW J,Xu HB,Wang Y X 2009Phys.Status Solidi RRL.3 99
[33]Rogl P,Rudy E 1978J.Solid State Chem.24 175
[34]Rogl P,Nowotny H,Benesovs F 1970Monatsh.Chem.101 850
[35]Rogl P,Nowotny H,Benesovs F 1970Monatsh.Chem.101 27
[36]Kalish D,C lougherty E V,Kreder K1969J.Am.Ceram.Soc.52 30
[37]BsenkoL,LundstromT1974J.Less-Common Met.34 273
[38]Mun roR G 2000J.Res.Natl.Inst.Stand.Technol.105 709
[39]O’Neill H1934The Hardness of Metals and Its Measuremen t(London:Chapman and Hall)
[40]Teter D M1998MRS Bu ll.23 22
[41]Brazhkin V V,Lyapin AG,Hemley R J 2002Philos.Mag.A82 231
[42]Smith R L,Sand land G E 1922Proc.Institut.Mech.Engin.102 623
[43]G ilman J J 1975J.Appl.Phys.46 5110
[44]Teter D M,Hemley R J 1996Science271 53
[45]GaoF M2004Phys.Rev.B69 094113
[46]GaoF M2006Phys.Rev.B73 132104
[47]GuoX J,Li L,Liu Z Y,Yu D L,He J L,Liu R P,Xu B,Tian Y J,W ang HT2008J.Appl.Phys.104 023503
[48] Šimůnek A,VackářJ 2006Phys.Rev.Lett.96 085501
[49]Dai F Z,Zhou Y C 2016Sci.Rep.6 33085
[50]TaoQ,Zheng D F,ZhaoX P,Chen Y Li,Li Q,Li Q,W ang C C,Cui T,Ma Y M,W ang X,Zhu P W 2014Chem.Mater.26 5297
[51]Inorganic Crystal Structu re Database,http://icsd.ill.eu/icsd/index.php[2017-01-12]
[52]Liu Q,Peng W M,Peng F 2014Chin.Phys.Lett.31 086202
[53]Zhang Y K,W u L L,W an B,ZhaoY,GaoR,Li Z P,Zhang JW,Gou HY,MaoHK2016Phys.Chem.Chem.Phys.18 2361
[54]Oganov AR,G lass C W 2006J.Chem.Phys.124 244704
[55]Oganov AR,Lyakhov AO,Valle M2011Acc.Chem.Res.44 227
[56]W ang Y C,LüJ,Zhu L,Ma Y M2010Phys.Rev.B82 094116
[57]W ang Y C,LüJ,Zhu L,Ma Y M2012Comput.Phys.Commun.183 2063
[58]Zhang X X,W ang Y C,LüJ,Zhu C Y,Li Q,Zhang M,Li Q,Ma Y M2013J.Chem.Phys.138 114101
[59]Amsler M,Goedecker S 2010J.Chem.Phys.133 224104
[60]Pickard C J,Needs R J 2011J.Phys.:Condens.Matter23 053201
[61]Kolmogorov AN,Shah S,Margine E R,Kleppe AK,Jephcoat AP 2012Phys.Rev.Lett.109 075501
[62]W ang X L,Tian F B,W ang L,Jin X L,Duan D F,Huang X L,Liu BB,Cui T2013NewJ.Phys.15 013010
[63]Eremets MI,Gav riliuk AG,Trojan IA,DzivenkoD A,Boehler R 2004Nat.Mater.3 558
[64]W ei S L,Li D,LüY Z,Liu Z,Xu C H,Tian F B,Duan D F,Liu BB,Cui T2016Phys.Chem.Chem.Phys.18 18074
[65]Yu HY,Duan D F,Liu HY,Yang T,Tian F B,BaoK,Li D,ZhaoZ L,Liu BB,Cui T2016Sci.Rep.6 18918
[66]Yu HY,Duan D F,Tian F B,Liu HY,Li D,Huang X L,Liu Y X,Liu BB,Cui T2015J.Phys.Chem.C119 25268
[67]Lu X H,Kang L,Zhou L,Chen J,Ji Z M,CaoC H,Jin BB,Xu W W,W u P H,W ang X S 2008Chin.Phys.Lett.25 4076
[68]Zou Y T,W ang X B,Chen T,Li X F,Q i X T,W elch D,Zhu P W,Liu BB,Cui T,Li BS 2015Sci.Rep.5 10811
[69]ZhaoZ L,BaoK,Li Da,Duan D F,Tian F B,Jin X L,Chen C B,Huang X L,Liu BB,Cui T2014Sci.Rep.4 04797
[70]Zhang Y K,W u L L,W an B,Lin Y Z,Hu Q Y,ZhaoY,GaoR,Li Z P,Zhang JW,Gou HY 2016Sci.Rep.6 33506
[71]Li D,Tian F B,Duan D F,BaoK,Chu BH,Sha X J,Liu BB,Cui T2014RSC Adv.4 10133
[72]ZhaoZ L,BaoK,Tian F B,Duan D F,Liu BB,Cui T2016Phys.Rev.B93 214104
[73]Quand t A,Boustani I2005Chem.Phys.Chem.6 2001
[74]Oganov AR,Chen JH,GattiC,Ma Y Z,Ma Y M,G lass C W,Liu Z X,Yu T,Ku rakevych OO,SolozhenkoV L 2009Nature457 863
[75]Boustani I1997Phys.Rev.B55 16426
[76]Chen Z Q,Peng Y S,Hu M,Li C M,LuoY T2016Ceram.Int.42 6624
[77]Dudka AP,Khrykina ON,Bolotina N B,Shitsevalova N Y,Filipov V B,SluchankoN E 2017J.Alloys Compd.692 535
[78]Ma T,Li H,Zheng X,W ang S M,W ang X C,ZhaoHZ,Han S B,Liu J,Zhang R F,Zhu P W,Long Y W,Cheng J G,Ma Y M,ZhaoY S,Jin C Q,Yu X H2017Adv.Mater.29 1604003
[79]Akopov G,Yeung MT,Sobell Z C,Tu rner C L,Lin C W,Kaner R B2016Chem.Mater.28 6605
[80]Troc R,W awryk R,Piku l A,Shitsevalova N 2015Philos.Mag.95 2343
[81]Li X F,Du J Y 2016RSC Adv.6 49214
[82]Li P F,Zhou R L,Zeng X C 2015ACS Appl.Mater.In terfaces7 15607
[83]Pan Y,Huang HW,W ang X,Lin Y H2015Comput.Mater.Sci.09 1
[84]Zhang X Z,ZhaoE J,W u Z J 2015J.Alloys Compd.632 37
[85]Yan Q,W ang Y X,W ang B,Yang J M,Yang G 2015RSC Adv.5 25919
[86]Huang B,Duan Y H,Hu W C,Suna Y,Chen S 2015Ceram.Int.41 6831
[87]Feng SQ,GuoF,Li J Y,W ang Y Q,Zhang L M,Cheng X 2015Chem.Phys.Lett.635 205
[88]W u L L,W an B,ZhaoY,Zhang Y K,Liu HY,W ang Y C,Zhang JW,Gou HY 2015J.Phys.Chem.C119 21649
[89]Ding L P,Kuang X Y,ShaoP,Huang X F 2014Inorg.Chem.53 3471
[90]W ang Y C,W u L L,Lin Y Z,Hu Q Y,Li Z P,Liu HY,Zhang Y K,Gou HY,YaoY S,Zhang JW,GaoF M,MaoHK2015Phys.Rev.B92 174106
[91]Li Y W,HaoJ,Xu Y 2012Phys.Lett.A376 3535
[92]Harikrishnan G,Ajith KM,Chandra S,Valsakumar MC 2015Modelling Simu l.Mater.Sci.Eng.23 085006
[93]Pan Y,Lin Y H,GuoJ M,W en M2014RSC Adv.4 47377
[94]Bian Y,Liu X,Li A,W ang S,Liang Y 2015Mater.Res.Innovations19 178
[95]Cui L,W ang ML,Wang Y X 2014J.Phys.Soc.Jpn.83 114707.
[96]Pan Y,Lin Y H2015J.Phys.Chem.C119 23175
[97]Fan J,BaoK,Jin X L,Meng X X,Cui T2012J.Mater.Chem.22 17630
[98]Ayd in S,Simsek M2009Phys.Rev.B80 134107
[99]Aronsson B1960Acta Chem.Scand.14 1414
[100]Meng X X,Fan J,BaoK,Li F F,Huang X L,Li Y,Tian F B,Duan D F,Jin X L,Zhu P W,He Z,Zhou Q,GaoC X,Liu BB,Cui T2014Chin.Phys.B23 016102
[101]Cheng X Y,Zhang W,Chen X Q,Niu HY,Liu P T,Du K,Liu G,Li D Z,Cheng HM,Ye HQ,Li Y Y 2013Appl.Phys.Lett.103 171903
[102]GaoF M,He J L,W u E D,Liu SM,Yu D L,Zhang S Y,Tian Y J 2003Phys.Rev.Lett.91 015502
[103]Chen X Q,Niu HY,LiD Z,Li Y Y 2011Intermetallics19 1275
PACS:61.05.–a,61.50.–f,62.50.–p,64.90.+bDOI:10.7498/aps.66.036104
Design of u ltra-hard mu ltifunctional transition metal compounds∗
BaoKuo Ma Shuai-Ling Xu Chun-Hong Cui Tian†
(State Key Laboratory of Superhard Materials,College of Physics,Jilin University,Changchun 130012,China)(Received 13 January 2017;revised manuscript received 19 January 2017)
Transition metals have special characteristics,such as a large number of valence electrons,multi valence states,high electron density,etc.Introducing a light element,such as boron,carbon,nitrogen,oxygen,etc.intoa transition metal is an important means for searching the newmultifunctional hard materials.W ith the development ofab in tiocalculation,advance in computer and themore in-depth understanding of the nature of hardness,it is possib le todesign newmultifunctionalu ltra-hard transitionalmetalwith using the advanced structure searching software,which could nowserve as the experimental syntheses of thesematerials.In the present article,we introduce the design of ultra hard mu lti functional transition metalmaterials.We fi rst introduce some basic ideas of hardness and material design,then conduct some studies,afterwardswe discuss some diffi culties in this kind of research.Hopefu lly these results in the present study cou ld be helpful for designing and synthesizing the ultra-hard multifunctionalmaterials.
material design,hard materials,material simulation,transition metal compounds
10.7498/aps.66.036104
∗国家自然科学基金(批准号:51632002,51572108,11634004,51032001,11104103)、教育部长江学者和创新团队发展计划(批准号:IRT_15R 23)和国家自然科学基金国家基础科学人才培养基金(批准号:J1103202)资助的课题.
†通信作者.E-mail:cuitian@jlu.edu.cn
*Project supported by the National Natu ral Science Foundation of China(G rant Nos.51632002,51572108,11634004,51032001,11104103),the Programfor Chang jiang Scholars and Innovative Research Teamin University of Ministry of Education of China(Grant No.IRT_15R23),and the Fund for Fostering Talents in Basic Science of the National Natural Science Foundation of China(G rant No.J1103202).
†Corresponding author.E-mail:cuitian@jlu.edu.cn
