基于忆阻器的时滞混沌系统及伪随机序列发生器∗
2017-07-31吴洁宁王丽丹段书凯
吴洁宁王丽丹†段书凯
1)(西南大学电子信息工程学院,重庆 400715)2)(非线性电路与智能信息处理重庆市重点实验室,重庆 400715)(2016年6月21日收到;2016年10月7日收到修改稿)
基于忆阻器的时滞混沌系统及伪随机序列发生器∗
吴洁宁1)2)王丽丹1)2)†段书凯1)2)
1)(西南大学电子信息工程学院,重庆 400715)2)(非线性电路与智能信息处理重庆市重点实验室,重庆 400715)(2016年6月21日收到;2016年10月7日收到修改稿)
忆阻器作为可调控的非线性元件,很容易实现混沌信号的产生.基于忆阻器的混沌系统是当下研究的热点,但是基于忆阻器的时滞混沌系统目前却鲜有人涉足.因此,本文提出了一个新型忆阻时滞混沌系统.时延的存在增加了系统的复杂性,使系统能够产生更丰富、更复杂的动力学行为.我们对提出的忆阻时滞混沌系统进行了稳定性分析,确定了显示系统稳定平衡点的相应参数区域.讨论了在不同参数情况下的系统状态,系统呈现出形态各异的混沌吸引子相图,表现出丰富的混沌特性和非线性特性.最后,将系统用于产生伪随机序列,并经过实验验证,我们提出的系统具有良好的自相关性和互相关性,同时能获得相对显著的近似熵.该时滞混沌系统具有复杂的动力学行为和良好的随机性,能满足扩频通信和图像加密等众多领域的应用需要.
忆阻器,时滞混沌,稳定性分析,随机性分析
1 引 言
忆阻器是Chua[1]于1971年提出的一种具有记忆功能的非线性电阻,2008年惠普(HP)实验室Strukov等[2]数学推导出了HP忆阻器模型,并且物理实现了忆阻器,制造出了世界上第一个忆阻器.此后,忆阻器日益受到学术界的重视,在非线性科学领域、神经网络领域、材料科学领域都得到广泛的关注和研究[3−6].忆阻器作为可调控的纳米级器件,在非线性领域有着巨大的应用前景,可以开拓性地推进这类传统领域的发展.由于忆阻器的电荷和磁通具有奇对称的特性[7,8],Itoh和Chua[9]运用一个磁通控制的分段线性忆阻器模型替换了蔡氏混沌电路中的蔡氏二极管,实现了第一个基于忆阻器的混沌系统.Muthuswamy和Kokate[10]采用运算放大器和乘法器等基本电子元件实现了一个忆阻器等效电路,并用光滑忆阻器模型代替蔡氏混沌电路中的蔡氏二极管,实现了一些新的忆阻混沌电路.在这些开创性研究的推动下,越来越多的探索致力于各类忆阻混沌系统的研究[11−14].近年的研究中,基于忆阻器的多涡卷混沌系统、分数阶混沌系统、超混沌系统都呈现出了丰富的动力学特性[15−17],但是目前鲜有人提出基于忆阻器的时滞混沌系统.
自从提出描述生理控制系统的Mackey-G lass方程以来[18],越来越多的研究致力于探索时滞动力系统的动力学行为.时延的存在增加了系统的复杂性,使系统能够产生更丰富、更复杂的动力学行为.许多自然系统可以用非线性时滞微分方程(DDE)进行数学建模[19],比如白血病人的产血机制的Mackey-G lass模型、光学双稳态谐振器动力学的Ikeda系统、厄尔尼诺和南方涛动(ENSO)、神经网络、种群动态、肿瘤生长、基因调控网络、控制系统等[20−24].引入延迟的非线性系统中最主要的复杂性是相空间中有限维到无限维的变化,可能导致系统的不稳定性以及许多复杂的现象,比如混沌、超混沌、多稳定性、分岔、振荡消失等.混沌系统可以应用到保密通信系统、基于混沌的噪声发生器、传感器的改善以及机器人的运动功能中.由于这些原因,我们旨在设计能产生混沌现象的简单的时滞系统[25].因此,寻找一个封闭形式的数学函数作为非线性部分的时滞动力系统值得特别关注.此外,时滞混沌系统稳定性的分析和控制设计也是目前研究的热点,因为它们恰当地描述了真实的物理情况.
本文在经典Mackey-G lass系统的基础上,利用忆阻器的忆阻值和电荷之间的非线性函数关系,提出了一种新的非线性时滞混沌系统.我们对所提出的忆阻时滞混沌系统进行了稳定性分析,确定了系统相应的稳定平衡点的参数区域,讨论了系统在不同参数情况下的稳定性.发现了系统在不同参数情况下呈现出多样的混沌吸引子相图,具有丰富的混沌特性和非线性特性.新的时滞混沌系统所产生的伪随机序列具有良好的自相关性和互相关性,同时能获得相对显著的复杂度,表明本文所提出的新的时滞混沌系统具有复杂的动力学行为和良好的随机性,可以作为新型的扩频序列应用于信息安全领域中.本文下面的内容安排如下:第2部分介绍了本文提出的忆阻时滞混沌系统的数学模型;第3部分计算了系统的平衡点并对每个平衡点进行了稳定性分析,确定了系统的参数范围;第4部分发现了系统在不同参数情况下具有丰富的非线性运动轨迹,对其进行了数值仿真,并验证了系统在不同参数情况下的系统状态;第5部分通过对提出的系统所产生的伪随机序列的相关性和复杂度的计算和仿真,对忆阻时滞混沌系统的随机性和复杂性进行了研究和分析;第6部分对整个工作进行了总结.
2 一个新的时滞混沌系统模型
本文提出一个基于忆阻器的时滞混沌系统,其方程如下:
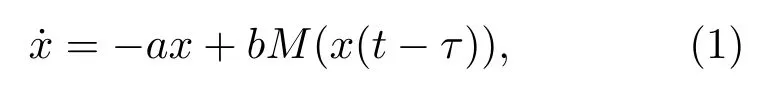
这里a,b是系统参数;τ是延迟时间;x(t)是忆阻器的电荷;M(.)表示忆阻值与电荷x之间的函数[14],
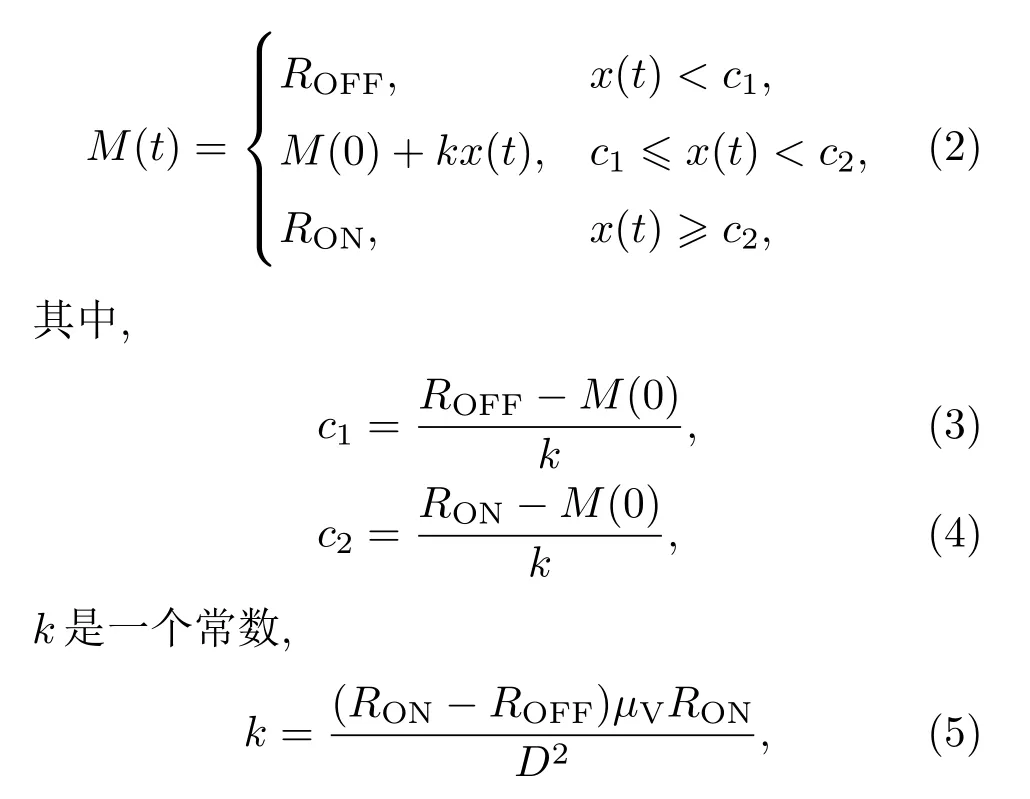
D是忆阻薄膜器件的厚度,M(0)是忆阻器的初始值,RON和ROFF分别代表当TiO2−x层的厚度为D和0时的极限忆阻值,µV是氧空穴的平均迁移率.本文中忆阻参数设置为:RON=10Ω,ROFF=2 kΩ, µV=10−15m2.s−1.V−1,M(0)=1 kΩ,D=1 nm.忆阻值与电荷x之间的函数关系如图1所示.

图1 忆阻器的忆阻值电荷的函数关系曲线Fig.1.Thememristance-charge curve ofmemristor.
3 平衡点分析
将方程(1)表示成如下形式以分析系统的稳定性:
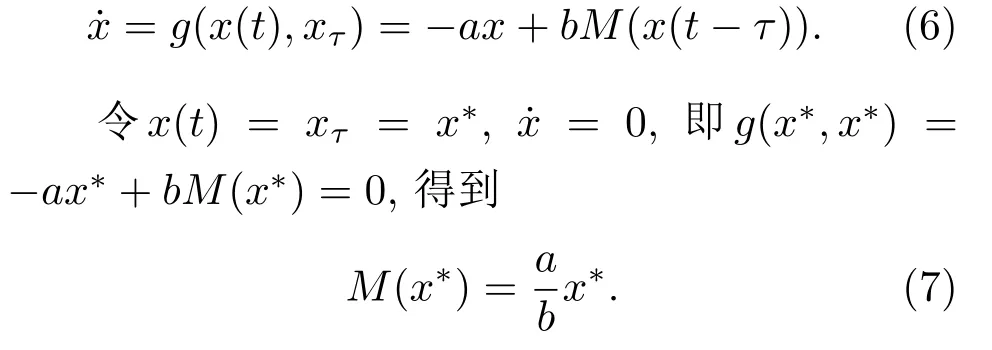
则我们得到系统的平衡点为
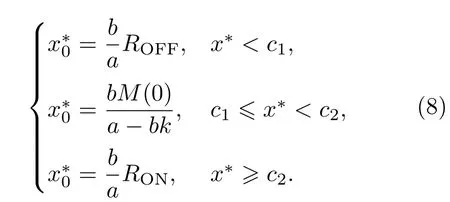
从(6)式,我们可以分别得到关于x和xτ的Jacobian矩阵,即
系统的特征方程为
3.1 τ=0时平衡点的稳定性
当τ=0时,由特征方程(11)式可以得到

1)当x∗<c1时,系统的平衡点为,特征根λ=−a;当x∗≥c2时,系统的平衡点为,特征根λ=−a.所以,在任意的参数a>0的情况下,都是稳定的平衡点.
2)当c1≤x∗<c2时,系统的平衡点为,特征根λ=−a+bk.当特征根λ存在负实部时,平衡点是稳定的.固当a>bk时,为稳定的平衡点.
由(5)式及相应的忆阻参数可知k的值为负数,固综上(1)和(2)式我们得到当τ=0时平衡点稳定的条件为

所以当τ=0,且参数a,b满足以上条件时,系统的平衡点为渐近稳定的.(13)和(14)式为选择系统参数的第一个条件.
3.2 τ/=0时平衡点的稳定性
在系统存在时延τ的情况下,对系统平衡点的稳定性讨论如下.
1)同样地,由(8)—(11)式可知,当x∗<c1和x∗≥c2时,τ>0时系统的平衡点和特征方程与3.1节讨论的τ=0时的平衡点和特征方程相同,即在任意的参数a>0的情况下,和都是稳定的平衡点.
2)当c1≤x∗<c2时,由(8)式,系统的平衡点为,此时系统的特征方程为一个指数方程:
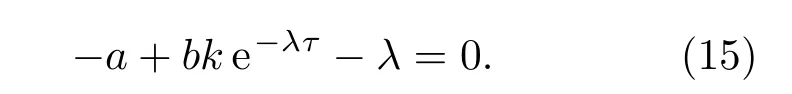
设λ=µ+i v,其中µ和v为实数.平衡点的渐近稳定性发生在特征方程所有的根都存在负实部时.如果µ的值从虚部变到实部,则µ<0代表稳定状态,µ>0代表分岔状态,µ=0代表极限情况,即当µ=0时平衡点的稳定性会发生改变,出现临界稳定曲线.下面我们假设µ=0,将λ=i v代入特征方程(11):
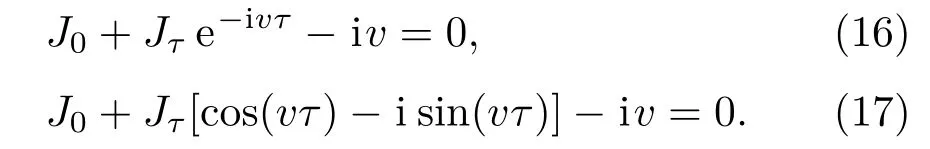
由(17)式的实部和虚部我们可以分别得到

联立(18)和(19)式可以得到
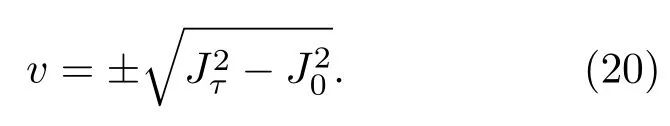
当且仅当|Jτ|>|J0|时成立,即|bk|>a(这里我们设a>0),(由忆阻参数知k的值为负).由(18)式可得到

这里n=0,±1,±2,...,当且仅当Jτ/=0,即bk/=0时成立.因此对于|Jτ|> |J0|及确定的v(当v> 0时),在(τ,a,b)参数空间中,对于任一曲线如果的值是负的,而其他曲线的值为正,则可以判定稳定域存在于的值为负的两条曲线之间:

(22)式中n=0,1,2,...,(23)式中n=1,2,...,n选取不同的值是为了分别满足两式中的τ为正.同样地,当v< 0时,存在一组与(22)和(23)式相同的方程,此时n的取值为负数,以保证τ的值为正.在τ> 0的条件下,为了确定曲线τ1(n),τ2(n)包含的稳定域,需要分析这些曲线对应的或者的特性,当导数的值为负时即为所求的临界曲线.由(11)式系统的特征方程,我们有
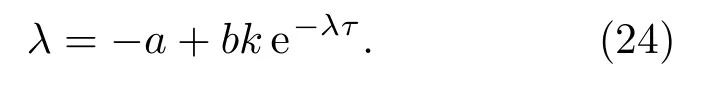
特征方程(24)式两边同时对τ求导:
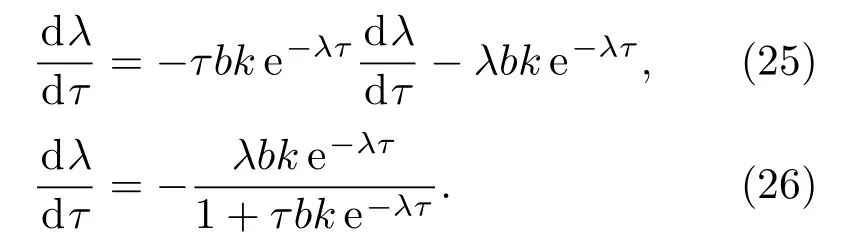
由(24)式可知,bk e−λτ= λ+a,代入(26)式:
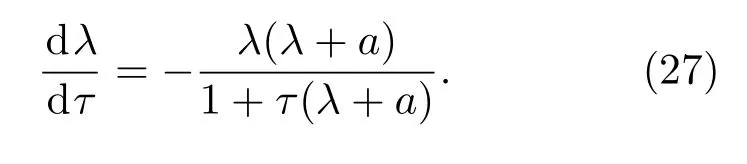
将µ=0时λ=i v代入(27)式:

所以(28)式的实数部分为

因此可见

对于τ1(n)和τ2(n)均成立.由(24)式知,当τ=0时,λ=−a+bk,所以当bk−a<0时µ<0,平衡点是稳定的.我们注意到条件(30)式否定了多稳定域的存在,因为若有第二个稳定域存在,当n>0时存在的曲线,但是由以上的推导得出所有的的值均为正,不存在这样的曲线,并且稳定域不存在于任意两个相邻的τm(n)(m=1,2)之间[19].以上这些条件都意味着这里只存在一个稳定域:即在(a,b)参数空间中的τ=0和(τ,a,b)参数空间中的临界曲线τ1(0)之间,紧邻τ=0的区域.图2中的实线部分为τ1(n)(n=0,1,2)、划线部分为τ2(n)(n=1,2).从以上分析我们得出,τ=0和τ=τ1(0)之间的区域是惟一的稳定域,由图2中的有色区域表示.其中对于τ1(0)来说,而在µ的负值到正值的范围内,其他曲线τ2(n)<τ<τ1(n)(n>0)都不满足所需的平衡条件,因此它们都属于非稳定域.
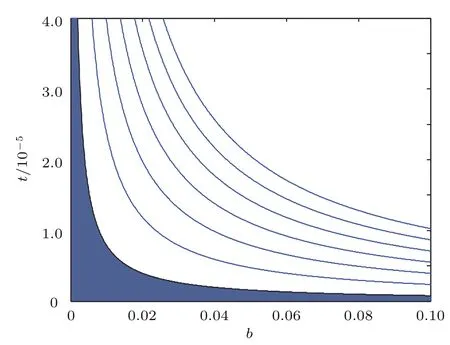
图2 (网刊彩色)a=1时参数空间τ-b的稳定域.实线部分表示τ1(n)(n=0,1,2),划线部分表示τ2(n)(n=1,2),阴影部分为平衡点的稳定域Fig.2.(color online)The stability region of the parameter spaceτ-b when a=1.The solid lines denote τ1(n)(n=0,1,2),the dashed lines denote τ2(n)(n=1,2)and the shaded area is the stability region of equilibriumpoint.
从以上的讨论中我们总结出c1≤x∗<c2时系统的平衡点的稳定性如下.
4 数值仿真
我们使用龙格库塔方法对系统方程(1)进行数值求解.通过选择不同的参数值可得到系统不同的动态范围.下面我们保持忆阻参数不变,研究当参数a,b,τ取不同值时,系统的动态变化.
这里保持忆阻参数的值不变以及令b=1,τ=1.61,改变参数a的值.当参数a的值在适当的范围内变化时,我们发现系统会呈现出不同的运动轨迹.其中当a的取值在1附近时,系统会产生混沌吸引子、周期轨道等丰富的动力学行为.图3显示了当a分别取0.7,0.8,0.992,1.1时系统的相图.由图3可以看出,系统对于参数a的变化极其敏感,参数a极小的改变都会使系统呈现出完全不一样的相图轨迹.由3.2节的分析可知,图3中的参数条件满足,此时系统的平衡点是渐近稳定的.
4.1 系统随参数a的变化

图3 保持b=1,τ=1.61,系统随参数a变化的相图 (a)a=0.7;(b)a=0.8;(c)a=0.992;(d)a=1.1Fig.3.Phase d iagramof the systemwith parameter a when keepb=1 andτ=1.61:(a)a=0.7;(b)a=0.8;(c)a=0.992;(d)a=1.1.
4.2 系统随参数b的变化
保持忆阻参数的值不变,我们令a=1,τ=1.61,改变参数b的值.由3.2节的分析我们知道,当时,特征方程(15)所有的特征根都存在负实部,所有τ1(n)和τ2(n)都是临界曲线,平衡点在整个参数范围内都是稳定的.现在我们取b的值小于这个临界值,观察其相图.由以上参数,可得,我们观察到,由于k的值极大,导致临界值极小,则此时满足b的值小于临界值的数量级变得很小.图4(a)—(c)中|b|的取值小于临界值,此时系统的平衡点是稳定的,我们观察到即使在参数b的值取这么小数量级的情况下,系统仍能产生混沌现象,并且混沌吸引子轨迹丰富、形态各异.同时,在实验中我们得到,当b的值大于并大于10−5时,系统都能产生形如图4(d)的混沌吸引子,并且随着参数b的变化,吸引子的形状不发生变化但吸引子的大小会随b的增加而增大,吸引子在坐标轴上的位置会随b的取值进行平移,相图中吸引子的中心坐标(x(t−τ),x(t))总是位于(10b,10b),如图4(d)所示.从图4显示的参数b取不同值时所对应的相图可以看出,当a=1,τ=1.61时,系统在参数b的动态范围内总是能呈现出丰富的混沌现象.
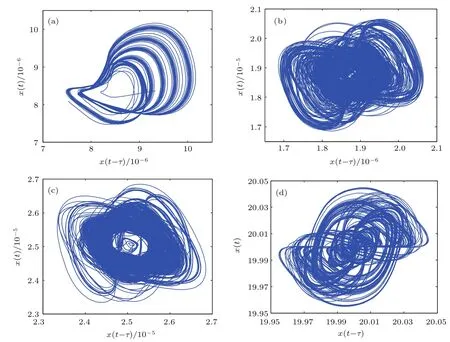
图4 当a=1,τ=1.61,参数b取不同的值时所对应的系统相图 (a)b=10−8;(b)b=3×10−8;(c)b=5×10−8;(d)b=2Fig.4.Phase diagramof the systemwith parameter b when keepa=1 and τ =1.61:(a)b=10−8;(b)b=3×10−8;(c)b=5×10−8;(d)b=2.
4.3 系统随时延τ的变化
令a=1,b=1以及保持忆阻参数值不变.如图5所示,当适当地改变时延τ的值时,系统呈现出形态各异的混沌吸引子相图.与图3和图4相比,改变时延τ比改变参数a或参数b的值时系统呈现出更多不同的运动轨迹,表现出了系统复杂的混沌特性和非线性特性.并且图5(f)显示出,当τ=1.61时,系统的混沌现象最丰富.由3.2节分析可知,此时的参数条件满足b>−a/k,平衡点在τ∈(0,τ(0))的范围内是稳定的,在τ∈ (τ(n),τ(n+1))时是不稳定的. 由(22)式,此时,图5中所取的τ的值均不在(0,τ(0))的范围内,固此时系统的平衡点是不稳定的平衡点.
当a=1,b=1,τ=1.61时,系统的时域波形如图6所示.图6为x(t)和x(t−τ)相对于时间t的波形,可以看出系统产生的时间序列具有非周期性.系统对初值的敏感特性如图7所示,蓝色曲线为x0=10.005的时域波形,红色曲线为x0=10.0050001的时域波形.可以看到即使初始值只相差0.000001,时域波形在一段时间之后呈现出截然不同时域轨迹,表现出系统对初值变化的极端敏感性.图8显示了系统的频谱图,可以看出系统的频谱是连续谱,并且有一系列的峰值,进一步说明了系统(1)的混沌特性.

图5 当a=1,b=1,改变时延参数τ时所对应的系统相图 (a)τ=1.21;(b)τ=1.52;(c)τ=1.56;(d)τ=1.6;(e)τ=1.605;(f)τ=1.61;(g)τ=1.66;(h)τ=1.97Fig.5.Phase diagramof the systemwith parameterτwhen keepa=1 and b=1:(a)τ=1.21;(b)τ=1.52;(c)τ=1.56;(d)τ=1.6;(e)τ=1.605;(f)τ=1.61;(g)τ=1.66;(h)τ=1.97.
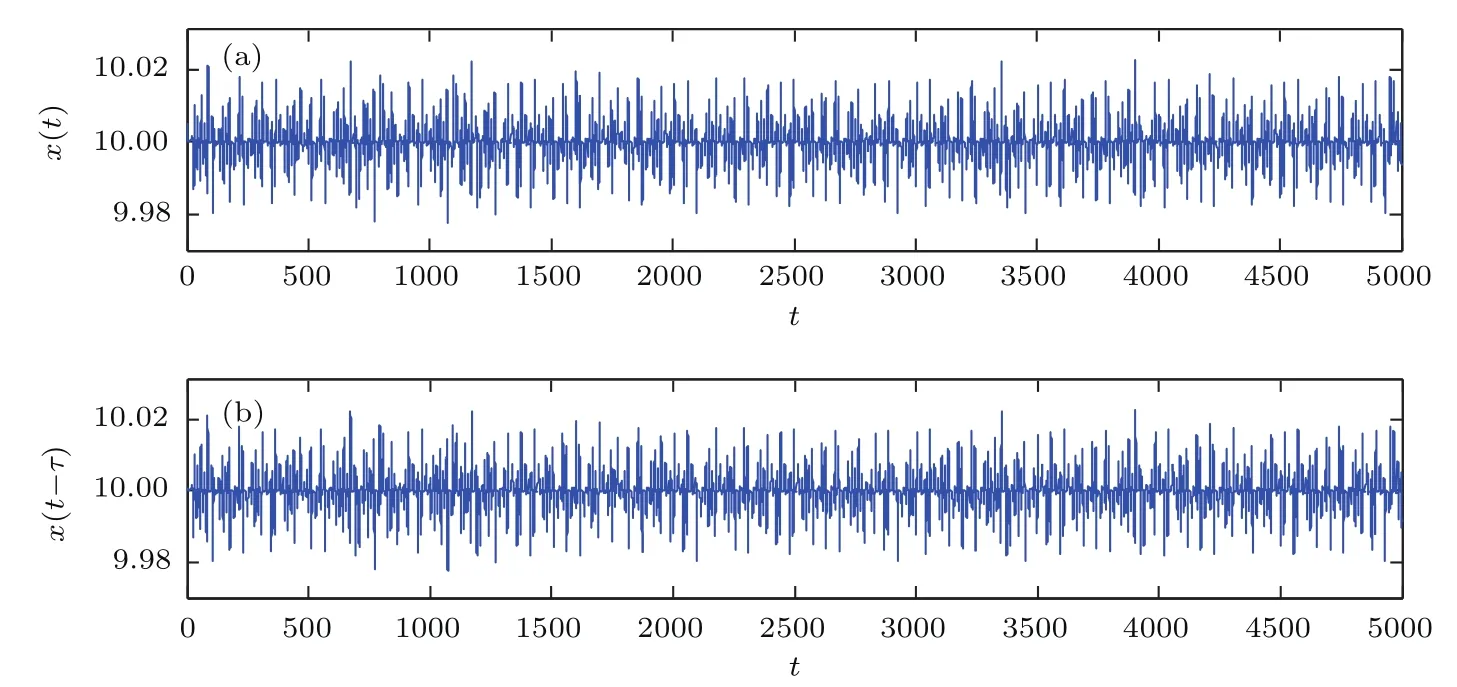
图6 时域波形图 (a)状态变量x(t)的时域波形;(b)状态变量x(t−τ)的时域波形Fig.6.The time domain waveform:(a)The time domain waveformof the state variab le x(t);(b)the time domain waveformof the state variab le x(t−τ).
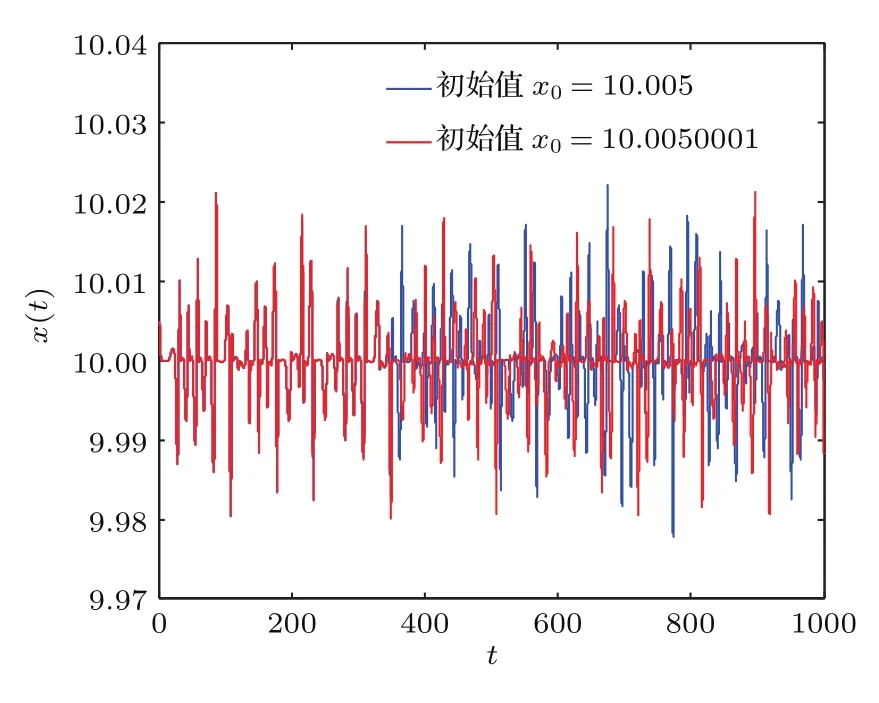
图7 (网刊彩色)状态变量x(t)对初值的敏感性Fig.7.(color on line)The sensitivity of the state variab le x(t).
5 混沌伪随机序列的特性
混沌运动虽然可以用确定的状态方程描述,但是其长期的行为表现出明显的不确定性和随机性.考虑到混沌系统天然的随机性,我们运用一种简单的截取混沌轨迹的部分或全部二进制比特的方法来产生伪随机序列,减少了算法代价:令Li=(30000×x)mod 255,再将Li转换为二进制数,并把所有Li(i=1,2,3,...,N)以二进制的形式连接起来保存为1×N的数组,即为此系统产生的混沌伪随机序列.
5.1 混沌伪序列相关性分析
二值伪随机序列的一个重要应用领域是可以用于扩频通信.在扩频通信中,扩频码的自相关函数特性决定扩频系统的多址、跟踪、捕捉和抗干扰能力,扩频码的互相关性决定扩频系统的抗多址干扰的能力.混沌序列相关特性的好坏,直接影响实际应用中的工作性能.
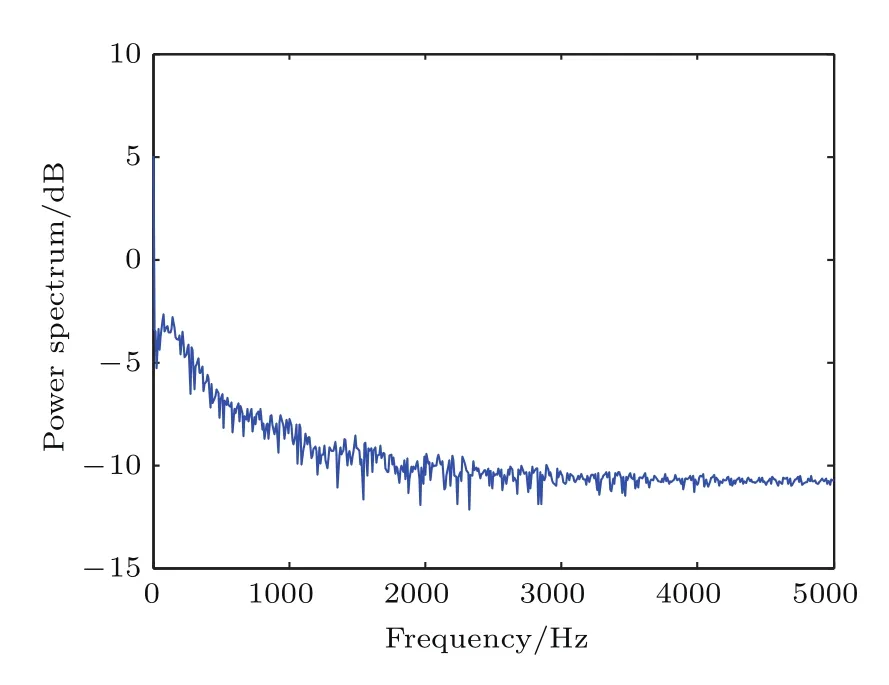
图8 系统的频谱图Fig.8.The power spectrumof systemtoinitial value.
设Lxi为关于x(t)的伪随机序列,Lyi为关于x(t−τ)的伪随机序列,则自相关函数为

互相关函数为
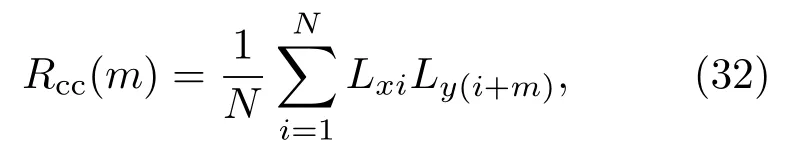
其中i=1,2,3,...,N,N为序列长度,m为相关间隔.
取N=40000,计算出时滞混沌序列的自相关和互相关特性的波形如图9所示.实验结果表明,忆阻时滞系统产生的伪随机序列具有良好的自相关性和互相关性.并且从相关性图9可以看出,本文忆阻混沌系统产生的相关特性波动小,比较稳定,能满足图像加密和扩频通信等众多领域的应用的需要.
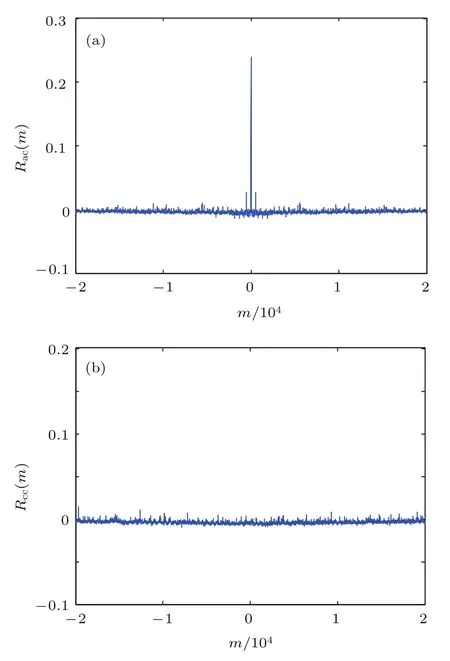
图9 新系统产生混沌序列的相关性 (a)自相关;(b)互相关Fig.9.The correlation of chaotic sequences generated by the newsystem:(a)Self-correlation;(b)crosscorrelation.
5.2 时滞混沌系统复杂度分析
混沌伪随机序列作为新型的扩频序列可以应用于信息安全领域中,所以对混沌伪随机序列的复杂度分析显得尤为重要.近似熵、模糊熵等方法可以描述混沌轨道随时间演化信息的产生率,并以此来度量混沌序列的复杂程度和随机性[26].计算近似熵的方法如下:
对于一个长度为N的序列L(1),L(2),...,L(N),定义一个m维的向量组X(1),X(2),...,X(i),...,X(N −m+1)∈ Rm,其中,
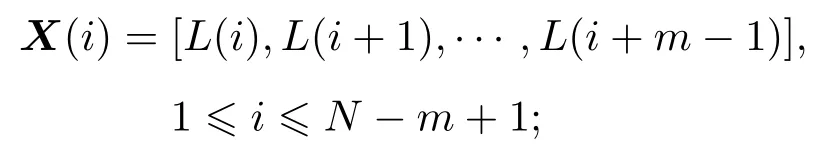
取任意两向量对应元素之间差值的绝对值的最大值,计算出任意向量X(i)与X(j)之间的最大距离
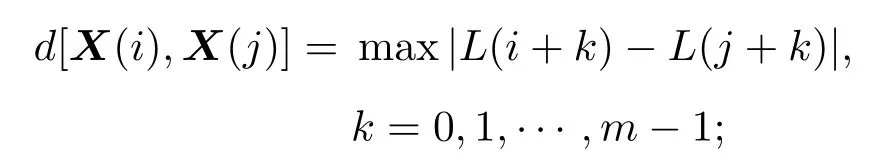
给定一个阈值r(r>0),对于第i个X(i),将满足条件d[X(i),X(j)]<r的个数与N−m的比值定义为
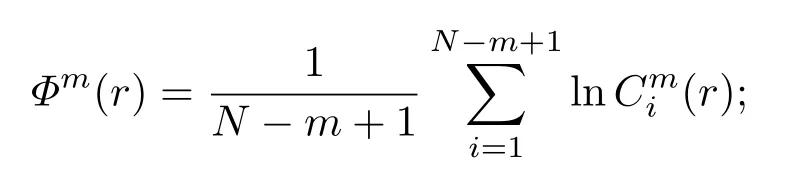
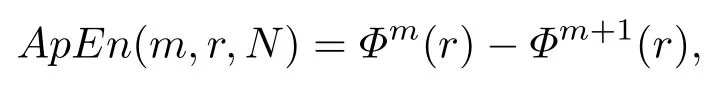
ApEn表示向量集随着m的增大产生信息的概率,产生信息概率越大,ApEn的值就越大,固序列的复杂度越大,它反映了混沌运动的复杂程度.
对于混沌伪随机序列而言,由于伪随机序列的取值是离散的,是一种特殊情况.因为计算ApEn要求选择较小的r,所以r的取值可以选择离散序列集的最小距离,这里对于混沌伪随机序列我们选择r=0.
按照上述方法求近似熵,我们令N=4000,m=2,r=0,分别求出四个时滞混沌系统所产生的随机序列复杂度,计算结果如表1所列.从表1中四个时滞混沌系统所产生的随机序列对应的近似熵的值可看出,本文所提出的新的忆阻时滞混沌系统产生的混沌伪随机序列的近似熵相对较大,说明新系统的复杂度很高,表明了本文新的忆阻时滞混沌系统具有潜在的混沌优势.
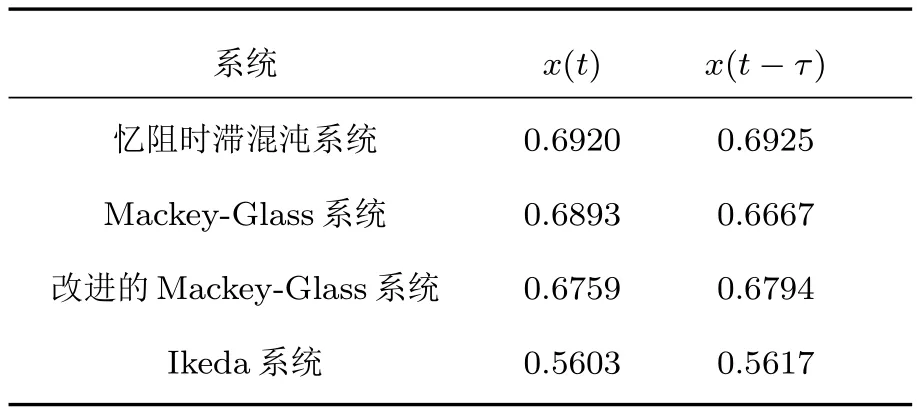
表1 混沌系统产生伪随机序列的近似熵Tab le 1.Approximate entropy of pseudorandomsequence generated by time-delayed chaotic system.
6 结 论
为了获得更为复杂的动力学行为的混沌吸引子,不断改善混沌系统已成为混沌动力学研究中的重要课题.因此,本文提出了一个具有复杂动力学行为的新的忆阻时滞混沌系统.本文利用忆阻器天然的非线性特性,构造出将忆阻值与电荷之间的函数关系作为非线性部分的具有单个延迟时间的新的时滞混沌系统.通过对系统的稳定性分析,确定了适当的时延参数和系统参数.并分析了参数变化对系统动力学行为的影响,用数值仿真描述了一系列具有不同时间延迟参数和系统参数的相图,不同的参数组合和细微的参数改变便可使系统呈现完全不同的相图轨迹,同时也验证了系统具有丰富的非线性特性.将系统用于产生伪随机序列,验证了系统所产生的伪随机序列具有良好的自相关性和互相关性,同时获得了相对显著的复杂度,表明本文所提出的新的时滞混沌系统具有丰富和复杂的动力学行为以及良好的随机性,可以作为随机序列发生器应用于信息安全领域中.
[1]Chua L O1971IEEE Trans.Circ.Theor.18 507
[2]Strukov D B,Snider G S,Stewart D R,W illiams R S 2008Nature453 80
[3]CorintoF,Ascoli A,G illiM2011IEEE Trans.Circuits Syst.I,Reg.Papers.58 1323
[4]JoS H,Chang T,Ebong I,Bhadviya BB,Mazumder P,Lu W 2010NanoLett.10 1297
[5]Yang J J,Pickett MD,Li X,Oh lberg D A,Stewart D R,W illiams R S 2008Nat.Nanotech.3 429
[6]W ang L D,Li HF,Duan S K,Huang TW,W ang HM2016Neurocompu ting171 23
[7]Sah MP,Yang C,KimH,Chua L 2012Sensors12 3587
[8]Hu X F,Chen G R,Duan S K,Feng G 2014In Memristor Networks(Springer International Pub lishing)pp351–364
[9]Itoh M,Chua L O2008In t.J.Bifurcat.Chaos18 3183
[10]Muthuswamy B,Kokate P P 2009IETE Tech.Rev.26 417
[11]BaoBC,Liu Z,Xu J P 2010E lectron.Lett.46 228
[12]Min G Q,W ang L D,Duan S K2015Acta Phys.Sin.64 210507(in Chinese)[闵国旗,王丽丹,段书凯 2015物理学报64 210507]
[13]Stork M,Hrusak J,Mayer D 2009In ternational Conference on Electrical and Electronics Engineering,2009 ELECOBu rsa,Tu rkey,November 5–8,2009 pp58–60
[14]W ang L D,D rakakis E,Duan S K,He P F,LiaoX F 2012Int.J.Bifurcat.Chaos22 1250205
[15]Li HF,W ang L D,Duan S K2014In t.J.Bifurcat.Chaos24 1450099
[16]Cafagna D,G rassi G 2012Non linear Dyn.70 1185
[17]Yang Y F,Leng J L,Li Q D 2014Acta Phys.Sin.63 080502(in Chinese)[杨芳艳,冷家丽,李清都2014物理学报63 080502]
[18]Mackey MC,G lass L 1977Science197 287
[19]Lakshmanan M,Senthilkumar D V 2011Dynamics of Non linear Time-Delay Systems(Springer Science&Business Med ia Press)pp27–36
[20]Ikeda K,DaidoH,AkimotoO1980Phys.Rev.Lett.45 709
[21]Bou tle I,Taylor R HS,Römer R A2007Am.J.Phys.75 15
[22]W u F X 2009Adv.Complex Syst.12 3
[23]LiaoX X,Chen G R 2003Int.J.Bifurcat.Chaos13 207
[24]Lu JQ,CaoJ D,HoD W C 2008IEEE Trans.Circuits Syst.I,Reg.Papers55 1347
[25]Zhang X M,Chen J F,Peng J H2011In t.J.Bifurcat.Chaos21 2547
[26]Guan G R,W u C M,Jia Q 2015Acta Phys.Sin.64 020501(in Chinese)[官国荣,吴成茂,贾倩2015物理学报64 020501]
PACS:05.45.Ac,05.45.Pq,05.45.Tp,02.30.KsDOI:10.7498/aps.66.030502
Amemristor-based time-delay chaotic systems and pseudo-randomsequence generator∗
Wu Jie-Ning1)2)Wang Li-Dan1)2)†Duan Shu-Kai1)2)
1)(School of Electronic and Information Engineering,Southweat University,Chongqing 400715,China)2)(Chongqing Key Laboratory of Non linear Circuits and Intelligent Information Processing,Chongqing 400715,China)(Received 21 June 2016;revised manuscript received 7 October 2016)
memristor,time-delayed chaotic,stability analysis,randomness analysis
10.7498/aps.66.030502
Memristor,a controllable nonlinear element,is easy togenerate a chaotic signal.More significantly,it can improve the complexity of the chaotic systemand the randomness of signals.Although thememristor chaotic systemis a hot spot of research currently,little attention has been paid tothe memristive time-delayed chaotic system.Therefore,a newmemristor-based time-delayed chaotic systemis proposed in this paper.We construct the time-delayed chaotic systemwith single delay time by using the non linear relationshipbetween the memristance and charge ofmemristor.The existence of time delay enhances the complexity of chaotic system,which makes the systemproduce richer and more complex dynamics.In order tostudy the complex dynamic characteristics of thismemristive time-delayed system,we investigate the proposed systemby theoretical derivation,numerical simulation,stabilization of equilibriumpoints,and power spectrum.In addition,the corresponding parameter region of the stable equilibriumpoint of the systemis discussed in detail.Then,we discuss the eff ect of parameter variation on the dynamic behavior of the system,and a series of phase diagrams with diff erent time-delayed parameters and systemparameters is described by numerical simulation.We find that diff erent combinations of parameters and slight changes of parameters can make the systema completely diff erent phase diagram,which indicates that the proposed systemhas rich nonlinear characteristic.Moreover,the proposed time-delayed systemis used togenerate pseudorandomsequences,and the experimental resu lts showthat the proposed systemhas good self-correlation,cross-correlation,and the significant approximate entropy.According tothe theoretical analyses and experimental results,we conclude that the proposed newtime-delayed chaotic systemhas complex dynamic behavior and good randomness,which can meet the needs of the applications in spread spectrumcommunication,image encryption and many other fields.This research provides a significant reference for further studying the usage ofmemristor.
∗国家自然科学基金 (批准号:61372139,61672436,61571372)、新世纪优秀人才支持计划(批准号:教技函[2013]47号)和中央高校基本科研业务费专项资金(批准号:XDJK2016A001,XDJK2014A009)资助的课题.
†通信作者.E-mail:ldwang@swu.edu.cn
*Project supported by the National Natu ral Science Foundation of China(G rant Nos.61372139,61672436,61571372),the Programfor NewCentury Excellent Talents in University of Ministry of Education of China(G rant No.[2013]47),and the Fundamental Research Funds for the Central Universities,China(G rant Nos.XDJK2016A001,XDJK2014A009).
†Corresponding author.E-mail:ldwang@swu.edu.cn
