基于领域相似度的复杂网络节点重要度评估算法∗

阮逸润老松杨 王竣德 白亮 陈立栋

(国防科学技术大学,信息系统工程重点实验室,长沙 410073)(2016年9月20日收到;2016年10月14日收到修改稿)

基于领域相似度的复杂网络节点重要度评估算法∗

阮逸润†老松杨 王竣德 白亮 陈立栋

(国防科学技术大学,信息系统工程重点实验室,长沙 410073)(2016年9月20日收到;2016年10月14日收到修改稿)

节点重要性度量对于研究复杂网络鲁棒性与脆弱性具有重要意义.大规模实际复杂网络的结构往往随着时间不断变化,在获取网络全局信息用于评估节点重要性方面具有局限性.通过量化节点局部网络拓扑的重合程度来定义节点间的相似性,提出了一种考虑节点度以及邻居节点拓扑重合度的节点重要性评估算法,算法只需要获取节点两跳内的邻居节点信息,通过计算邻居节点对之间的相似度,便可表征其在复杂网络中的结构重要性.基于六个经典的实际网络和一个人工的小世界网络,分别以静态与动态的方式对网络进行攻击,通过对极大连通系数与网络效率两种评估指标的实验结果对比,证明了所提算法优于基于局域信息的度指标、半局部度指标、基于节点度及其邻居度的W L指标以及基于节点位置的K-shell指标.

复杂网络,鲁棒性,节点重要性,领域相似度

1 引 言

随着以互联网为代表的网络信息技术的高速发展,人类社会的网络化趋势已十分明显,人们的日常生活越来越多地依赖于各种复杂网络系统安全可靠的运行.实际复杂网络的无标度特性[1]与小世界特性[2],使得网络中的一些特殊节点对于网络的结构和功能有着巨大的影响,我们将这些节点称为重要节点,当网络中这部分重要节点失效时,其影响将快速波及到整个网络.因此,如何准确量化网络节点的重要性,挖掘出其中的关键节点意义重大.例如,在传染病传播网络中[3,4]对网络关键节点进行接种免疫可有效抑制病毒传播,预防其大规模爆发;在电力网中,对关键地区电路采取预防措施,可有效避免电力网络的级联失效[5,6];在大规模路由网络中,对关键路由节点采取有效防护措施,可有效避免路由节点遭受攻击时对网络的毁灭性破坏.

近年来,节点重要性度量是网络科学研究的一个热点,衍生出许多经典的节点重要性排序算法,包括度排序[7]、接近中心性排序[8]、介数中心性排序[9]、特征向量排序[10],PageRank[11,12],LeaderRank[13]与H指数[14]等. 其中度(degree centrality)排序方法是一种简单有效的局部算法,接近中心性算法与介数中心性算法需要用到网络全局信息,算法时间复杂度过高,在应用上具有局限性.Chen等[15]提出半局部中心性(semilocal centrality)指标,该指标有限地扩大了节点领域的覆盖范围,很好地平衡了算法精度与时间复杂度的关系.王建伟等[16]认为节点的重要性由节点自身及其邻居节点的度数相关(W L centrality),即节点及其邻居的度越大,节点重要性越高;任卓明等[17]综合考虑节点的度数及其邻居的集聚程度,提出了一种基于邻居信息与集聚系数的节点重要性评价算法.Ugander等[18]发现邻居节点间的联通子图数目是节点重要性的决定因素.Kitsak等[19]提出了K-shell分解算法,该算法类似于剥洋葱的方法,通过剥离法将网络外围度数小的节点逐层剥除,位于内层的节点拥有较高的重要度,然而K-shell分解算法是一种粗粒化的排序方法,对于节点重要性的区分度不够.

上述节点重要性评价指标主要是基于网络鲁棒性与脆弱性的方法,事实上关键点检测与具体的研究背景紧密相关,在节点传播影响力以及网络可控性的背景下,节点重要性评价方式又有所不同.基于网络传播动力学模型[20]评价排序算法的研究成果丰硕.Chen等[21]认为节点影响力不仅由节点拥有的信息传播路径数量决定,同时还与传播路径的多样性紧密相关;Ruan等[22]通过弱化节点领域的聚簇性对节点影响力排序结果的影响,提出一种基于节点邻居核数与网络约束系数[23]的节点影响力排序算法;Li等[24]基于马尔可夫链分析,通过分析节点在网络中的动态行为用于评估节点影响力;最近,Liu等[25]分析了离散的网络SIR(susceptible-infected-recovered)传播动力学,同时考虑了传染率、康复率和有限的时间步三个参数用于寻找网络中最有影响力的节点.更多基于影响力传播效率的评价方法,可参见文献[26].而在复杂网络可控性[27,28]领域,如何寻找最佳的驱动节点使得系统达到期望的状态是该领域的基本问题,这类驱动节点可被认为是网络的重要节点.Zhou等[29]发现将网络的一些度数小但反馈增益高的节点作为驱动节点,可有效提高网络牵制控制的速度;Liu等[30]根据节点的出入度情况对节点在网络中的不同重要性做了有效的层级划分,并基于此提出一种改进策略用于有效打击网络的可控性能;Jia和Pósfai[31]基于随机抽样的方法,计算节点成为驱动节点的可能性,发现节点的入度越大越不容易成为驱动节点.目前有关网络可控性的研究方法已经逐渐丰富和全面,理解不同背景下的节点重要性含义对于将理论研究进行实践应用具有指导意义.

大规模实际复杂网络的结构往往随着时间发生变化,受技术条件的限制,对于很多极其复杂的网络获取其完整的网络结构数据依然十分困难,因而通过全局信息定义网络节点重要度具有局限性.通过量化节点局部网络拓扑的重合程度来定义节点间的相似性,本文提出了一种考虑节点度以及邻居节点拓扑重合度的节点重要性评估算法,算法只需要获取节点两跳内的邻居节点信息,通过计算邻居节点对之间的相似度,便可表征其在复杂网络系统中的结构重要性,在六个实际网络和一个人工小世界网络中的实验表明,所提算法相比度指标degree、半局部度指标semilocal、基于节点度及其邻居度的W L指标以及K-shell分解指标更能准确评估节点的重要性.

2 理论算法

节点在网络中的重要性不仅取决于节点本身的度数,还取决于邻域节点对该节点的依赖程度,这里的邻域节点特指两跳内的低阶邻居节点.如图1(a)所示,小型网络除节点a可分为被3个大的椭圆包围的3块,尽管节点a度数小于邻居节点b,c和d,但从网络瓦解的角度上分析,当节点a遭受攻击时,该小型网络将迅速分离为三个独立的网络,对网络的破坏性最大.不仅如此,从信息传播的角度分析,从每一块中的任一节点到其他块中的任一节点的信息的传输都必然要经过节点a,因此信息从节点a发起将有更大的概率传播到网络中的大部分区域.若图1(a)中节点a邻居节点的邻域存在如图1(b)中的交集,即a的邻居b和c有3个共同邻居,此时节点a的枢纽地位受到削弱,网络的鲁棒性将增强.通过量化节点局部网络拓扑的重合程度,我们定义了节点领域相似度,节点领域相似度越高,网络对于节点的依赖程度越低,节点的结构重要度也越低.图1(b)中,当邻居节点b和c之间不存在连边时,b与c的相似度定义为Jaccard指标[32]值,即sim(b,c)=|n(b)∩n(c)|/|n(b)∪n(c)|,若b和c之间存在连边如图1(c),定义sim(b,c)=1,即

sim值介于0和1之间,节点局部网络拓扑的重合程度越高,则节点相似度值越大.按照(1)式,在图1(a)中,可得sim(b,c)=1/9,在图1(b)中,sim(b,c)=4/9.在图1(c)中,节点b和c之间存在连边,则sim(b,c)=1.

节点的邻居数目越多,且邻居间的网络拓扑重合程度越低,节点在网络结构和功能中的作用越不容易被其他节点所替代,节点重要度越高.综合考虑邻居节点间的相似性,我们提出了一种基于邻域相似度的重要度评估指标LLS(i),表示为

n(i)表示节点i的邻居节点,LLS指标综合考虑了节点的度与邻居节点的相似度,LLS值越大,说明节点的度越大且其邻居节点之间邻域重合程度越低.仍以图1中的节点a为例,在图1(a)中,

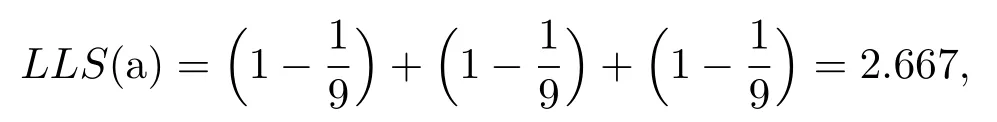
若节点b和c的邻域产生如图1(b)中的交集,则

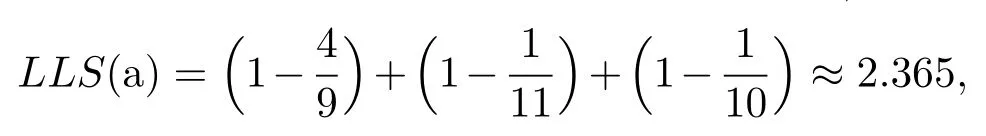
更进一步,若b与c还发生了连接,则

可见,节点a的邻居节点间拓扑结构重合度越高,a的结构重要性将越低,计算结果值验证了我们的设想.

图1 (网刊彩色)节点a的领域重合情况Fig.1.(color on line)Overlapbetween the topologies of the neighbors of node a.

3 评价标准

常用来评价节点重要性排序算法的方法有基于网络的传播动力学模型以及基于网络鲁棒性与脆弱性的方法.在不同的评价模型中,节点重要性的含义有所区别,在SIS(susceptible-infectioussusceptible)[19]模型中一个节点的重要度由稳态下该节点被感染的概率决定;在SIR[33]模型中,一个节点的重要度由该节点的平均传播范围决定.本文基于网络鲁棒性对算法排序结果进行评价,主要研究渗流中的最大连通子图,采用极大连通系数与网络效率指标量化移除节点后对于网络结构与功能的影响,以此评价节点的结构重要性.

1)极大连通系数:将节点按照重要度评估算法从大到小进行排序,观察移除一部分节点后对网络极大连通子集(网络巨片)[34]的影响,计算公式如下:

其中,N表示网络中节点总数,R表示移除一部分节点后的网络巨片的节点数,网络巨片规模随着节点移除而变小的趋势越明显,表明采用该方法攻击网络的效果越好.

2)网络效率:考察移除节点对于网络效率的影响[35,36],网络效率可用于评价网络的连通性强弱,移除网络中的节点及其对应的所有边,使得网络中的某些路径被中断而导致一些节点之间的最短路径变大,进而使整个网络的平均路径长度增大,影响网络连通性.网络效率表示为

其中,ηij=1/dij,dij表示节点i和j之间的最短路径,N表示网络节点数.本文通过删除网络中一定比例的特定节点,模拟网络遭受攻击的仿真效果,计算网络遭受攻击前后的网络效率下降比例用以量化各个节点重要性评价指标的准确性.网络效率下降比例表示为:µ=1−η/η0,η表示移除节点后的网络效率,η0表示原始的网络效率,0≤µ≤1.µ的值越大,表示移除节点后网络效率变得越差.

4 实验数据集

为了验证LLS指标评估节点重要性的效果,本文选取6个具有不同拓扑结构特性的真实网络以及一个5000个节点规模的人工小世界网络,网络的拓扑结构统计特征如表1所列:1)Facebook网络数据,SlavoZitnik的脸谱网朋友圈关系数据[37];2)USAir美国航空网络[38];3)Infectious人群感染网络[39];4)Email邮件网络[40];5)Yeast蛋白质相互作用网络[41];6)Power美国国家电力网络[42].表1中N与M分别代表网络节点总数与连边数;〈k〉代表网络平均度大小;ksmax表示K-shell分解后网络核心层的核值,ksmin表示K-shell分解后网络最外层的核值;L为节点间平均最短路径长度.

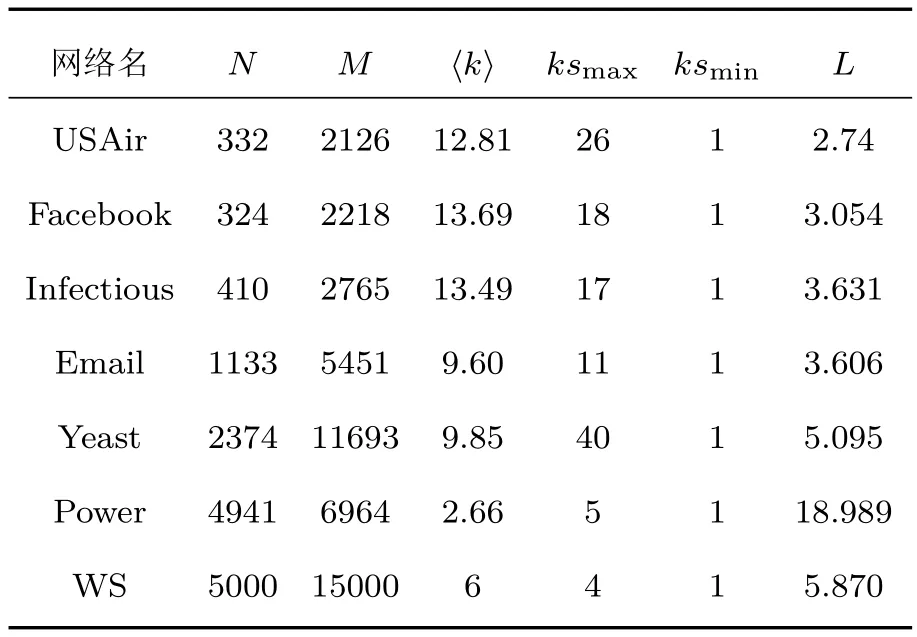
表1 六个真实网络和一个人工小世界网络的拓扑特征Tab le 1.Structu ral properties of six real networks and one artifi cial small-world network.

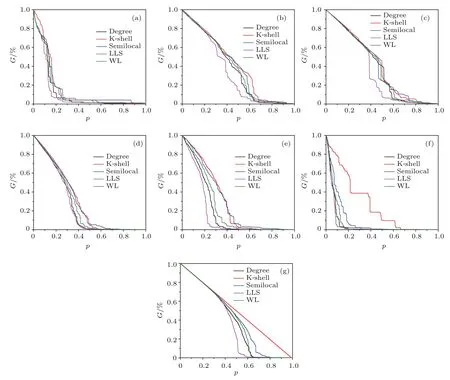
图2 (网刊彩色)利用不同指标攻击网络重要节点后极大连通系数G的变化 (a)美国航空网络;(b)脸谱网;(c)人群感染网;(d)邮件网络;(e)蛋白质相互作用网络;(f)美国西部电力网;(g)小世界网络Fig.2.(color online)The relative size of giant component(G)sub jectswith diff erent static attack strategies:(a)USAir;(b)Facebook;(c)In fectious;(d)Email;(e)Yeast;(f)Power;(g)Small-world network.

5 实验结果与分析

基于上述6个真实网络以及人工小世界网络,本文对LLS指标与同样是采用局域信息的度排序方法(degree)、半局域度排序方法(semilocal)、基于节点度及其邻居度的排序方法(W L)以及基于节点位置信息的K-shell分解方法进行了比较和分析.根据五种算法的排序结果,分别以静态攻击与动态攻击的方式移除一定比例p排名靠前的节点,模拟网络遭受蓄意攻击时极大联通子图规模与网络效率的变化情况,从而评价各个排序算法的准确性.在静态攻击模式中,节点重要度指标值保持与原始网络中各指标计算结果值一样,不随网络结构变化而重新计算;反之,在动态攻击模式中,每移除一个节点或一定比例的节点,节点的各个重要度指标需要重新计算一次.

5.1 静态攻击效果

在模拟蓄意攻击网络对网络极大连通系数的影响的实验中,分别对6个真实网络采用degree指标、K-shell分解指标、semilocal指标、W L指标以及本文提出的LLS指标移除排名靠前的节点,实验结果如图2(a)—(g)所示.在所有的网络中,LLS指标导致网络极大连通系数变小的总体趋势最为明显,尤其在图2(e)蛋白质互作用网络中,LLS指标在网络静态攻击的初始过程就表现出相比其他指标更好的攻击效果.图2(f)红色曲线为模拟通过K-shell分解方法找出的网络核心节点用于攻击Power网络的结果,曲线中存在部分网络极大连通系数不随着最大K-shell节点的移除而下降的情况,这是由于在静态攻击模式中,原本重要度排序靠前的节点其真实重要度已随着网络结构的变化而变化,且K-shell方法容易将局域连接过于紧密的小团体判断为网络核心节点[43,44],而这些伪核心节点并不在网络极大连通子图中.在图2(g)小世界网络的巨片瓦解实验中,K-shell分解方法瓦解网络的效率最差,类似随机攻击的结果,其原因是小世界网络中节点度分布较为均匀,K-shell分解方法对于网络节点重要度的区分能力有限.

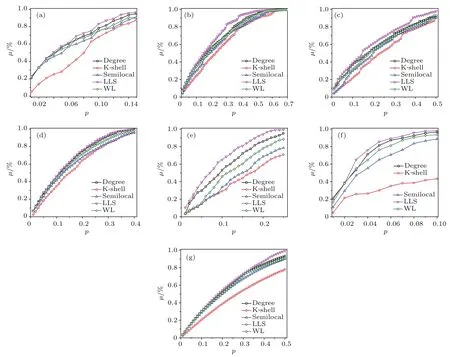
图3 (网刊彩色)利用不同的节点重要性指标删除一定比例排序靠前的节点后网络效率下降率µ的变化 (a)美国航空网络;(b)脸谱网;(c)人群感染网;(d)邮件网络;(e)蛋白质相互作用网络;(f)美国西部电力网;(g)小世界网络Fig.3.(color on line)The relation between decline rate of network effi ciencyµand the number of key nodes removed fromthe network,the ranking lists are produced by diff erent ranking ind ices:(a)USAir;(b)Facebook;(c)In fectious;(d)Email;(e)Yeast;(f)Power;(g)Small-world network.

图3反映的是利用不同的节点重要性指标删除一定比例排序靠前的节点后,网络效率下降率µ的变化,移除重要节点后网络连通性越差,网络效率的下降趋势越明显.实验结果如图3(a)—(g)所示,采用LLS指标删除排序靠前的节点导致网络效率下降的幅度最大,其后依次是度指标、半局部度指标、W L指标、K-shell指标.例如在图3(f)的美国西部电力网中,选择性删除各个指标排序靠前的1%至10%的节点,与其他指标相比,利用LLS指标删除节点后,网络效率变得最差.

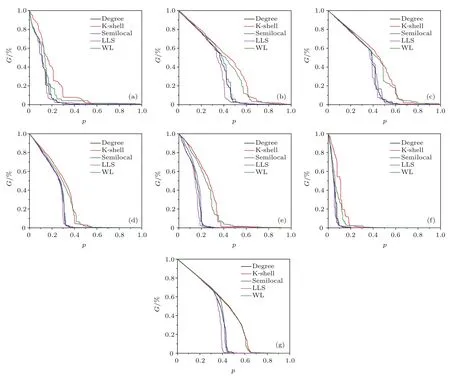
图4 (网刊彩色)利用不同指标动态攻击网络重要节点后极大连通系数G的变化 (a)美国航空网络;(b)脸谱网;(c)人群感染网;(d)邮件网络;(e)蛋白质相互作用网络;(f)美国西部电力网;(g)小世界网络Fig.4.(color on line)The relative size of giant component(G)sub jects with d iff erent dynamic attack strategies:(a)USAir;(b)Facebook;(c)In fectious;(d)Email;(e)Yeast;(f)Power;(g)Small-world network.

5.2 动态攻击效果

网络遭受蓄意攻击时结构会发生变化,因此节点的重要度排序结果也将随之改变,静态攻击方式不考虑网络结构变化对节点重要度排序结果的影响,是一种相对简单的攻击方式,与之对应的动态攻击方法则是在每一轮网络攻击后重新计算网络中各节点的重要度.基于上述四个网络,本文比较了LLS指标、degree指标、semilocal指标、W L指标以及K-shell指标对网络进行动态攻击时的效果,如图4和图5所示,在网络极大连通系数与网络效率的实验中,利用LLS指标动态移除排序靠前的节点,网络碎片化效果最明显,攻击效果最佳.同时,通过将图2与图4、图3与图5进行对比,不难发现,对于一种特定的重要度排序方法,动态攻击的效果总是好于静态攻击的效果.尤其在小世界网络中的对比更为明显,观察图2(g)与图4(g)两种攻击模式下的网络瓦解效果,发现动态攻击方式明显优于静态攻击.

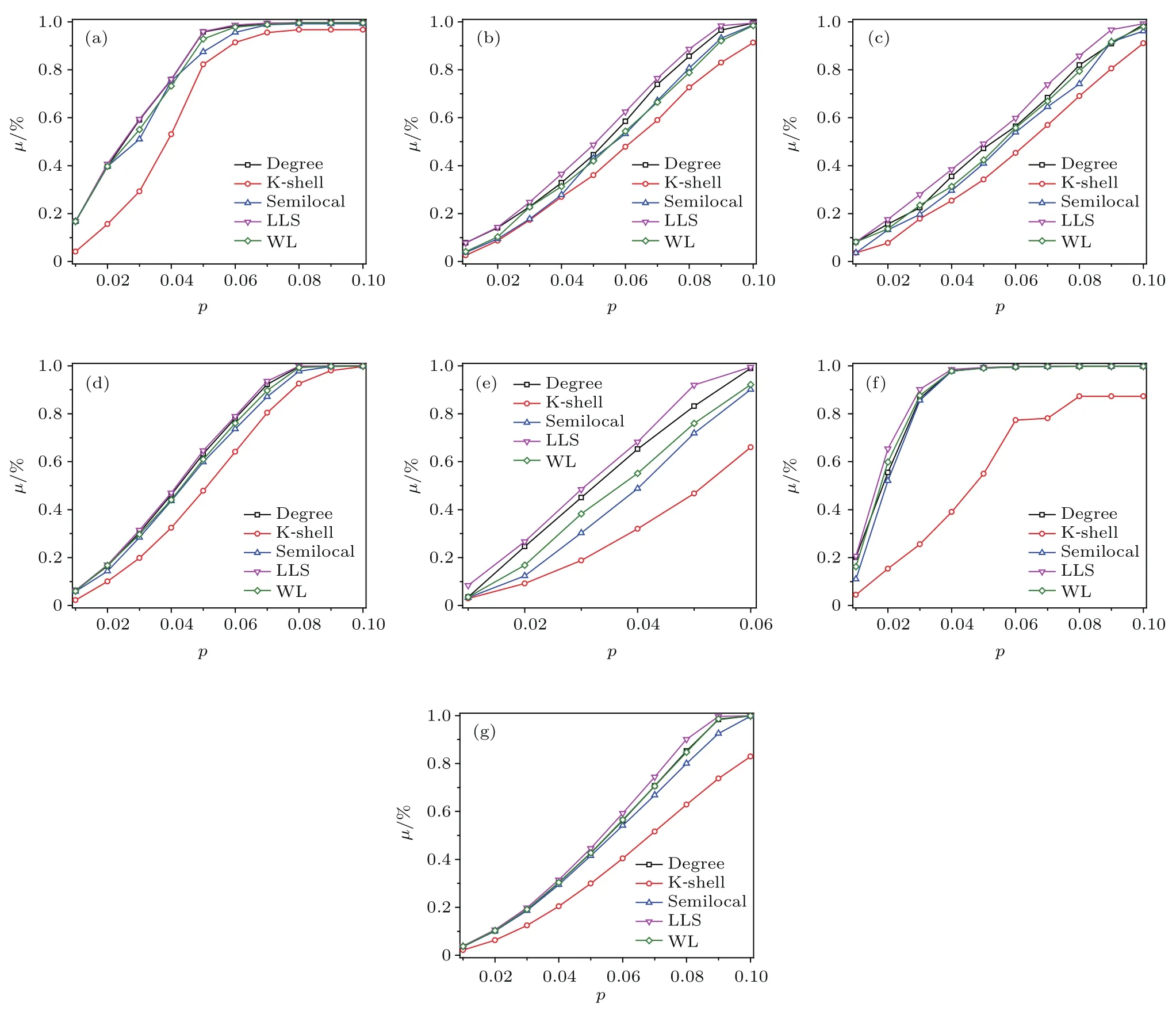
图5 (网刊彩色)利用不同的节点重要性指标动态删除一定比例排序靠前的节点后网络效率下降率µ的变化,节点重要度在每一轮攻击行为发生后都进行了重新计算 (a)美国航空网络;(b)脸谱网;(c)人群感染网;(d)邮件网络;(e)蛋白质相互作用网络;(f)美国西部电力网;(g)小世界网络Fig.5.(color on line)The relation between decline rate of network effi ciencyµand a certain proportion of themost important nodes removed fromthe network,the ranking lists are recalcu lated after each round of attack behavior:(a)USAir;(b)Facebook;(c)In fectious;(d)Email;(e)Yeast;(f)Power;(g)Small-world network.

6 结 论

识别复杂网络中的关键节点可以帮助我们有效地设计防护策略用于提高网络枢纽节点的安全防护能力,对于提升网络抗毁性与结构稳定性有重要作用.通过量化节点局部网络拓扑的重合程度来定义节点间的相似性,本文提出了一种考虑节点度以及邻居节点拓扑重合度的节点重要性评估算法,算法只需要获取节点二跳内的邻居信息就可计算出节点的重要度值,因而对于刻画大规模网络的抗毁性与结构可靠性具有现实意义.在实际网络和人工的小世界网络中,通过对极大连通系数与网络效率两种评估指标的实验结果对比,证明了所提算法优于基于局域信息的度指标、半局部度指标、基于节点与邻居度的W L指标以及基于节点位置的K-shell指标.

本文从结构的角度分析了单层网络中的节点重要性,近年来,越来越多的网络科学工作者将研究的目光从孤立的单层网络转移到相互依存的网络上[45],在相依网络中一旦某个节点遭到破坏而失效,网络间的依存关系将会使得失效的影响被传播和放大,最终一个很小的故障就可能导致整个网络的瘫痪.因此如何在相互关联的网络中分析节点对于网络的结构鲁棒性与功能稳定性的影响具有重要意义,这是我们下一步研究的方向.

[1]Barabási AL,Albert R 1999Science286 509

[2]W atts D J,Strogatz S H1998Nature393 440

[3]Pastor-Satorras R,Vespignani A2001Phys.Rev.Lett.86 3200

[4]Rogers T2015Europhys.Lett.109 28005

[5]Kinney R,Crucitti P,Albert R,Latora V 2005Eur.Phys.J.B46 101

[6]W ang G Z,CaoY J,BaoZ J,Han Z X 2009Acta Phys.Sin.58 3597(in Chinese)[王光增,曹一家,包哲静,韩祯祥2009物理学报58 3597]

[7]Albert R,Jeong H,Barabási AL 1999Nature401 130

[8]Sabidussi G 1966Psychometrika31 581

[9]Freeman L C 1977Sociometry40 35

[10]Newman ME J 2006Phys.Rev.E74 036104

[11]Brin S and Page L 1998Comput.Networks.Isdn.30 107

[12]Radicchi F,FortunatoS,Markines B,VespignaniA2009Phys.Rev.E80 056103

[13]LüL Y,Zhang Y C,Yeung C H,Zhou T2011P loSOne6 e21202

[14]LüL Y,Zhang Q M,Stanley HE 2016Nat.Commun.7 10168

[15]Chen D B,Lu L Y,Shang MS,Zhang Y C,Zhou T2012Physica A391 1777

[16]W ang JW,Rong L L,GuoTZ 2010J.Da lian Un iv.Technol.50 822(in Chinese)[王建伟,荣莉莉,郭天柱2010大连理工大学学报50 822]

[17]Ren ZM,ShaoF,Liu JG,GuoQ,W ang BH2013Acta Phys.Sin.62 128901(in Chinese)[任卓明,邵凤,刘建国,郭强,汪秉宏2013物理学报62 128901]

[18]Ugander J,BackstromL,MarlowC,Kleinberg J 2012Proc.Natl.Acad.Sci.109 5962

[19]Kitsak M,Gallos L K,Hav lin S,Liljeros F,Muchnik L,Stan ley HE,Makse HA2010Nat.Phys.6 888

[20]Ren X L,LüL Y 2014Sci.Bu ll.59 1175(in Chinese)[任晓龙,吕琳媛 2014科学通报 59 1175]

[21]Chen D B,X iaoR,Zeng A,Zhang Y C 2014Europhys.Lett.104 68006

[22]Ruan Y R,LaoS Y,X iaoY D,W ang J D,Bai L 2016Chin.Phys.Lett.33 028901

[23]Bu rt R S 2009Structure Holes:the Social Structure of Competition(London:Harvard University Press)p53

[24]Li P,Zhang J,Xu X K,Small M2012Chin.Phys.Lett.29 048903

[25]Liu JG,Lin JH,GuoQ,Zhou T2016Sci.Rep.6 21380

[26]LüL Y,Chen D B,Ren X L,Zhang Q M,Zhang Y C,Zhou T2016Phys.Rep.650 1

[27]Liu Y Y,Slotine J J,Barabási AL 2011Nature473 167

[28]Orouskhani Y,JaliliM,Yu X H2016Sci.Rep.6 24252

[29]Zhou MY,ZhuoZ,LiaoH,Fu Z Q,Cai SM2015Sci.Rep.5 17459

[30]Liu Y Y,Slotine J J,Barabasi AL 2012PloS One7 e44459

[31]Jia T,PósfaiM2014Sci.Rep.4 5379

[32]Jaccad P 1901Bu ll.Torrey Bot.C lub37 547

[33]CastellanoC and Pastor-Satorras R 2010Phys.Rev.Lett.105 218701

[34]Dereich S,Mörters P 2013Ann.Prob.41 329

[35]Vragovic I,Louis E,D iaz-Guilera A2005Phys.Rev.E71 036122

[36]Latora V,MarchioriM2007NewJ.Phys.9 188

[37]Blagus N,Šubelj L,Bajec M2012Physica A391 2794

[38]Batagelj V,Mrvar A1998Connections21 47

[39]Isella L,StehléJ,Barrat A,CattutoC,Pinton J F 2011J.Theor.Biol.271 166

[40]Guimera R,Danon L,D iaz-Guilera A,G iralt F,Arenas A2003Phys.Rev.E68 065103

[41]Von Mering C,Krause R,Snel B,Cornell M,Oliver S G,Fields S,Bork P 2002Nature417 399

[42]W atts D J,Strogatz S H1998Nature393 440

[43]Liu Y,Tang M,Zhou T,DoY 2015Sci.Rep.5 9602

[44]Liu Y,Tang M,Zhou T,DoY 2015Sci.Rep.5 13172

[45]Bu ldy rev S V,Parshani R,Pau l G,Stan ley HE,Hav lin S 2010Nature464 1025

PACS:89.75.Fb,89.75.HcDOI:10.7498/aps.66.038902

N ode importance measu rement based on neighborhood similarity in complex network∗

Ruan Yi-Run†LaoSong-Yang Wang Jun-De Bai Liang Chen Li-Dong

(Science and Technology on Information Systems Engineering Laboratory,National University ofDefense Technology,Changsha 410073,China)(Received 20 September 2016;revised manuscript received 14 October 2016)

Ranking node importance is of great signifi cance for studying the robustness and vulnerability of complex network.Over the recent years,various centrality indices such as degree,semilocal,K-shell,betweenness and closeness centrality have been employed tomeasure node importance in the network.Among them,some well-known globalmeasures such as betweenness centrality and closeness centrality can achieve generally higher accuracy in ranking nodes,while their computation complexity is relatively high,and alsothe global information is not readily available in a large-scaled network.In this paper,we propose a newlocalmetric which on ly needs toobtain the neighborhood information within twohops of the node torank node importance.Firstly,we calculate the similarity of node neighbors by quantifying the overlapof their topological structures with Jaccard index;second ly,the similarity between pairs of neighbor nodes is calculated synthetically,and the redundancy of the local link of nodes is obtained.Finally,by reducing the in fluence of densely local links on ranking node importance,a newlocal index named LLS that considers both neighborhood similarity and node degree is proposed.Tocheck the eff ectiveness of the proposed method of ranking node importance,we carry out it on six realworld networks and one artificial small-world network by static attacks and dynamic attacks.In the static attack mode,the ranking value of each node is the same as that in the original network.In the dynamic attack mode,once the nodes are removed,the centrality of each node needs recalculating.The relative size of the giant component and the network effi ciency are used for network connectivity assessment during the attack.Afaster decrease in the size of the giant component and a faster decay of network effi ciency indicate a more eff ective attack strategy.By comparing the decline rates of these twoindices toevaluate the connectedness of all networks,we find that the proposed method ismore effi cient than traditional localmetrics such as degree centrality,semilocal centrality,K-shell decomposition method,nomatter whether it is in the static or dynamicmanner.And for a certain rankingmethod,the resu lts of the dynamic attack are always better than those of the static attack.This work can shed some light on howthe local densely connections aff ect the node centrality in maintaining network robustness.

complex network,robustness,node importance,neighborhood similarity

10.7498/aps.66.038902

∗国家自然科学基金(批准号:61571453)资助的课题.

†通信作者.E-mail:ruanyirun@163.com

*Project supported by the National Natural Science Foundation of China(G rant No.61571453).

†Corresponding author.E-mail:ruanyirun@163.com