三角形分类教学中培养学生平面几何理性思考能力的实践研究
2017-07-31姜霄虹
姜霄虹
三角形分类教学中培养学生平面几何理性思考能力的实践研究
姜霄虹
以“三角形分类(1)”一课为例,探索如何在平面几何图形教学中提高学生发现特征的能力、对特点间关系的思考能力,以及根据特点的逻辑表征能力;利用“先示范后模仿”的教学形式,既使学生学到了三类三角形的定义以及如何辨别三类三角形,又发展了学生学习平面几何的三种重要能力即发现能力、思考能力以及逻辑表征能力。
三角形分类 发现能力 思考能力 逻辑表征能力
一、 教学的理性思考
“三角形的分类(1)”是沪教版数学第四册“几何小实践”单元中的教学内容。通过这节课的学习,学生知道锐角三角形、直角三角形和钝角三角形的定义,并且学会按角的组成特点将三角形分为三类。
三角形是重要的平面几何图形研究对象之一。比起长方形和正方形,探究三角形的特征对学生的要求更高。因为长方形和正方形都为四个直角,角的大小是固定的;而三角形的三个内角大小是不固定的,其中两个是锐角,第三个角却是动态的,它可以是锐角、钝角,也可以是直角。学生要能够发现三角形的与众不同之处,就需要对平面图形的特征有较强的发现能力。同时,学生还要能根据角的特征将三角形分成三类,需要其具有较强的根据图形间的特点进行有效思考的能力。最后,根据三角形的特征进行命名,并且分别给三类三角形下定义,即三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,需要学生拥有较好的逻辑表征能力。
以上能力也是研究其他平面几何图形特点的基石,为学生学习更复杂的平面几何图形打下扎实的基础。因此在“三角形分类(1)”一课中,教师应探究如何提高学生发现平面几何图形特征的能力、对特点间关系的思考能力,以及根据特点进行逻辑表征的能力。
二、对“三角形分类(1)”的实践探索
学习“三角形的分类(1)”前,学生已认识了锐角、直角和钝角的概念,积累了以图形边的条数或角的个数作为标准的分类经验后,此课将通过抓住三角形中角的特点,进一步划分三角形。
(一)激活图形分类经验,引出课题
教学片段1
师:图1是小兔留下的图形,小朋友你能按图形的特点分一分吗?两人互相交流。
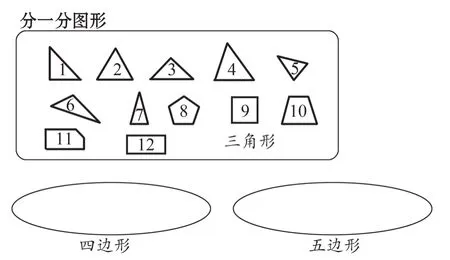
图1
生:1,2,3,4,5,6,7分成一组,因为都是三角形;9,10,12分成一组,因为都是四边形;8,11分成一组,都是五边形。
师:同意的小朋友点点头。我们来看看小兔朱迪怎么分?它和你们是一样的。
师:左边框里都是四边形,它们有什么特点?
生:四边形有四条边,四个角。
师:那么五边形呢?三角形呢?我们按照图形角的个数、边的条数来分一分,那么同一类图形,比如这些三角形,可以再分一分吗?今天我们来学习三角形的分类。
师:有了分一分黑板上图形的经验与方法,你认为三角形的分类可以按什么来分?
生:三角形能不能按大小分?
生:三角形能不能按边分?
生:三角形能不能按角分?
师:今天我们先按角的特点来分一分三角形。首先复习有关角的知识,你能运用学过的本领把这些角送回家吗?请大家独立完成连一连(见图2)。
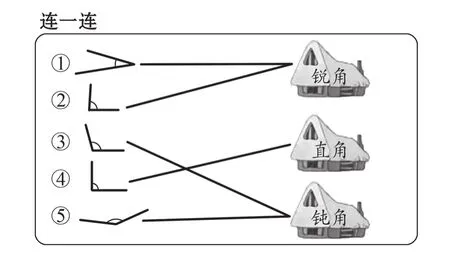
图2
在此教学环节中,教师出示了12个平面图形,其中有三角形、四边形和五边形,要求学生分一分,意在激活学生已有的分类经验,以图形的边和角作为要素,以此为分类标准进行分类。
学生在分类的过程中,从具体的图形入手,明确了各种平面图形的要素是边和角,也唤醒了以边的条数、角的个数等要素特点作为分类标准的分类经验。既然图形的分类是按角的个数和边的条数不同为标准,同样由三个角组成的三角形是否也能以角的类型不同分一分?因此在教授新课前,教师有针对性地复习相关角的概念,既激活了学生对相关概念的记忆,也唤醒了学生的分类经验,渗透了类比的数学思想,作为后续三角形分类的迁移经验的铺垫。
另外,在明确图形的分类主要是以边和角作为依据后,在讨论分类的标准时,教师通过提供问题框架,引导学生提出“三角形能不能按大小分?”“三角形能不能按边分?”和“三角形能不能按角分?”三种想法,培养其发散性思维和逻辑思维,建立平面几何图形的一般思考方法。
(二)同中求异找出分类特征,对三类三角形下定义
1. 寻找类特征,进行分类
教学片段2
师:注意黑板上的三角形(见图3),它们的角是什么角,你知道吗?请同学们自行标注一下。
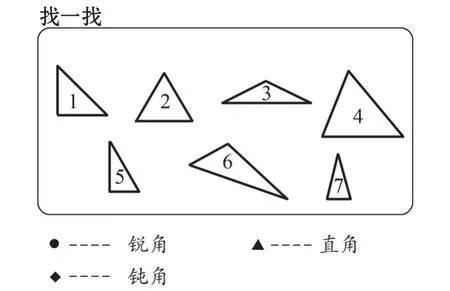
图3
师:大家都找到每个三角形中角的特点,根据这些特点,两人合作,分一分三角形的类型。
生:三角形可以分成三类:1,5一类,因为它们都有一个直角和两个锐角;3,6一类,它们都有一个钝角和两个锐角;2,4,7分为一类,它们都有三个锐角。
师:和前两类不同,你发现最后一类三角形中三个角都是锐角。
在上一环节中,教师激活了学生已有的锐角、直角、钝角的概念,以及对三角形和多边形分类的经验,在此环节则侧重于将角的概念与三角形分类建立联系。教师可以设计教学活动使学生在量一量、做标记的过程中,对三角形的角用图形进行编码,根据每个三角形三个角不同的组成情况进行分类。在此环节中,首先,学生不受三个内角的大小影响,在同一个三角形中根据角的大小情况,把三个角分类,并且概括了三角形是由哪些角组成,发展了自身对平面几何图形特征的发现能力。其次,学生认为这些三角形根据其角的组成情况可以分成三类,分别是三个角都是锐角的三角形,有两个锐角、一个钝角的三角形和有两个锐角、一个直角的三角形。在第二次找特征的过程中,学生从在一个三角形找特征到在多个三角形中找共同特征,并且通过比较各个三角形中角的组成情况,概括出三角形的类特征,对图形的特点进行有效思考。
2. 归纳特征,给三角形“取名字”
教学片段3
师:根据三角形角的特点,你们把它们分成三类。那你能给它们分别起个名字吗?
生:第一类是直角三角形。
师:第一类三角形除了一个直角,明明还有两个锐角,为什么要叫直角三角形呢?
生:因为其他三角形也有两个锐角,而直角只有第一类三角形才有。
师:有了这个经验,第二类三角形叫作什么?第三类呢?
生:钝角三角形,第三类叫锐角三角形。
师:在数学史上,给三角形分类时,和你们一样,经历了找一找、分一分,最后根据它们的特点给三角形们起了名字,接下来请大家把书翻到第56页,一边读一边比一比,前人找到的特点是什么?和你们哪里不同?
师:小朋友你能把刚才分类起名字的过程总结成小经验吗?
在“取名字”的环节中,学生能在交流讨论、正确与错误的碰撞过程中,挑选出每一类三角形的独有特点,对把握三类三角形特征起着关键的作用。
然而,在描述钝角三角形、直角三角形的定义时,学生仍旧用“有两个锐角和一个钝角的三角形是钝角三角形;有两个锐角和一个直角的三角形是直角三角形”定义两类三角形。通过看书反思,学生回溯之前自己的定义,在比较的过程中,不仅再一次强化三类三角形的特点,也对数学简洁精准的语言有了新的认识与感受,在今后的数学学习中能优化自己的语言表述,使语言更加简洁且精准,促进了学生的逻辑表征能力的发展。
(三)同中求异,在一类中定量揭示角的特点,铺垫后续学习
教学片段4
师:在锐角三角形中,仔细观察,比一比图3中2号三角形三个角的大小,你认为左下角和右下角大小关系怎么样?有没有办法证明呢?
生:把三角形对折,两个角大小相等。
师:那么上面的角和它们相比呢?请操作,你会发现什么?
生:三个角大小都相等。
师:那么还有两个三角形的三个角的大小又有怎样的关系?
生:7号三角形有两个角相等,4号三角形三个角都不相等。
师:锐角三角形按照角的大小还能再分成三种,这是我们以后进一步研究的知识。那么钝角三角形、直角三角形呢?挑选一类三角形,两人商量一下,也像老师一样验证一下。
(学生独立进行探究活动)
师:不管是直角三角形、钝角三角形,还是锐角三角形,都有两个角相等或者三个角都不相等的情况,而锐角三角形还有三个角都相等的特殊情况。三年级时,这些发现将帮助我们继续学习关于三角形另一部分重要的知识。
经过了按角分类三角形的过程,学生初步感知了在同一种图形中可以继续分类。本环节引导学生思考在同一类三角形(即锐角三角形、直角三角形和钝角三角形)中也存在异同。教师以锐角三角形为例,引导学生以角的大小作为特点来观察。学生通过观察、比较、操作,发现锐角三角形、钝角三角形、直角三角形都有两个角相等和三个角都不相等的情况,并且锐角三角形还有三个角全相等的情况。在操作的过程中,激活了学生直接比较和间接比较的活动经验,即通过对折发现两个角是否相等,通过等量推断得知三个角都相等,培养了学生的定量思考能力,
三、 总结与反思
(一) 找类特征的同时发展学生的学习能力
通过对“三角形的分类”这一内容的理解、设计、实践、反思,笔者对此类课有了更多的认识。相对于传统教学,即以“先示范、后模仿”作为教学方式,本教学设计通过放手让学生量一量、想一想,放慢教学节奏,提供充足的时间给学生感悟,寻找并概括出类特征。此过程发展了学生对平面几何图形的认识能力;他们能够根据不同三角形角的不同组成情况分类,概括出类特征,发展了学生联系图形特点间的关系,并进行有效思考的能力;通过给三类三角形命名并说理的过程,发展了学生的逻辑表征能力。
(二)提出一些改进的想法
(1)在培养思考力的同时,适当引入智能化手段,运用现代科学技术,使三角形分类更加形象化,更加直观,易于学生理解。
(2)本节课教师对学生分类思考过程的了解,仅仅局限于个别回答了问题的学生,而对了解其他学生是如何思考的,如何评价每个学生的思考过程,仍然需要探索。此外,教师还可以组织学生评价哪种思考路径更加合理,引导其反思、总结自己的思考过程。
在今后的教学实践中,笔者也会不断尝试,以期以理解数学、理解学生为基准,选取恰当的教学内容,通过提出启发性问题,放手让学生探究,感悟数学知识,获得更多学习经验。
姜霄虹 上海市第一师范学校附属小学 200233
