直线驱动型并联机器人误差模型与灵敏度分析

于 今 余 伟 吴超宇 程 敏 钱小吾

(1．重庆大学机械传动国家重点实验室，重庆400044;2．镇江高等专科学校数理化工系，镇江212002)

直线驱动型并联机器人误差模型与灵敏度分析

于 今1余 伟1吴超宇1程 敏1钱小吾2

(1．重庆大学机械传动国家重点实验室，重庆400044;2．镇江高等专科学校数理化工系，镇江212002)

为提高直线驱动型并联机器人动平台末端执行器位置精度，根据并联机构结构和运动学模型，对影响末端位置精度的各项误差源进行了分析，利用解析法建立动平台末端操作空间与关节空间之间的误差映射模型;在灵敏度误差模型的基础上，依据全域灵敏度评价指标，提出了一种误差源筛选方案，筛选影响位置精度的主要误差源，利用蒙特卡洛法随机模拟并联机器人中各零部件的尺寸误差、驱动误差和装配误差，得知筛选前后动平台位置误差基本一致，验证了评价指标的正确性。以激光跟踪仪为测量工具在任务空间中取点测量，对筛选后的主要误差源进行辨识，修正并联机构的正向运动学模型后，并联机构末端位置精度改善显著，验证了误差源筛选方案的有效性和可行性，减轻了误差参数辨识的复杂程度和计算量，对结构较复杂的机构误差补偿具有一定的指导意义。

并联机器人;误差模型;全域灵敏度;误差源筛选方案

引言

并联机器人作为工业机器人的一个重要分支，虽然其具有负载能力强、速度快、重复性能好等多种优势而日益受关注，但精度差，没有进行标定的机器人，精度误差可以达到几毫米，因此在很多应用中必须对机器人进行精确标定。标定过程主要为:建立误差模型、仪器测量、误差参数辨识和误差补偿［1－3］。在4个步骤中，第3步误差参数辨识最为复杂、重要。因此很多学者在参数辨识这方面做了很多研究工作，参数辨识常用的算法有最小二乘法［4－5］，但由于其需要轨迹规划且计算量大，所以不实用。LEVENBERG-MARQUARDT算法将牛顿法和最陡下降法相结合，尽管该算法有收敛速度快和稳定性强等优势，但其需很大的内存［6－7］;扩展卡尔曼滤波法虽然是处理非线性系统的经典方法，但因其未考虑误差的分布情况并且认为状态误差可通过一个独立的线性系统产生，从而造成估计精度较低并容易出现滤波发散等情况［8］;随后，一些学者也提出了提高参数辨识效率的方法。MARCO等［9］对机器人冗余参数误差辨识进行了分析;KHALIL等［10］利用了辨识雅克比矩阵的条件数;唐国宝等［11］利用并联机构操作空间与关节空间非线性映射的性质，仅需检测末端z向的位置误差以及在初始位形的姿态误差便可辨识出几何参数;张文昌等［12］基于步进迭代法以实测信息与理想模型输出之间的残差构造误差辨识模型，进而辨识几何参数。

上述学者们提出解决几何参数误差辨识的方法都是在数学方法上作研究和探讨，本文在前人工作基础上，通过解析法建立动平台末端操作空间与关节空间之间的误差映射模型;在分析灵敏度误差模型的基础上，依据全域灵敏度评价指标，提出一种误差源筛选方案，对误差模型中的误差源进行简化，在保证末端位置精度的基础上，去除对位置精度影响较弱的误差源，减轻误差参数辨识的复杂程度和计算量，缩短计算时间，提高参数辨识效率，并通过激光跟踪仪误差标定实验验证所提出的误差源筛选方案的有效性和可行性。

1 结构模型介绍

直线驱动型并联机器人的三维模型示意如图1所示，该机构主体结构由静平台、动平台、同步带电缸、滑块、U型虎克铰、3组平行四边形支链杆件组成，每组支链分别通过2个虎克铰(U副)来连接动平台与滑块，滑块通过平移副(P副)由同步带电缸驱动。3个电机安装在同步电缸的上方，直线驱动3个滑块，杆件连接处采用一种特殊设计的U型虎克铰结构(图2)，该虎克铰采用U型铰链轴与单耳环相连，U型铰链可以通过键槽实现两侧的同向性，旋转副U1是U型连接轴绕连接轴的转动，可以实现360°转动，旋转副U2是单耳环绕轴的运动，设计的约束是－40°～40°，该结构能够保证平行四边形两组杆件的同向性，并能扩大关节的转动能力。平行四边形支链杆件可以保证动平台在平动时不发生翻转，并且采用炭纤维制造，质量小，体积小，具有较好的动态响应性能。

图1 直线驱动型并联机器人三维模型Fig．1 Three dimensionalmodel of linear driven parallel robot

图2 虎克铰示意图Fig．2 Schematic diagram of Hooke joint

针对直线驱动型并联机器人，由于有动平台和静平台，3组平行四边形支链，3个滑块，所以机构数n=1+1+3+3=8，包含有6个虎克铰以及3个移动副，所以运动副数量g=6+3=9，每个虎克铰包含2个转动副，每个移动副包括1个平移副，所以自由度fi之和为6×2+3=15。所以自由度之和M为

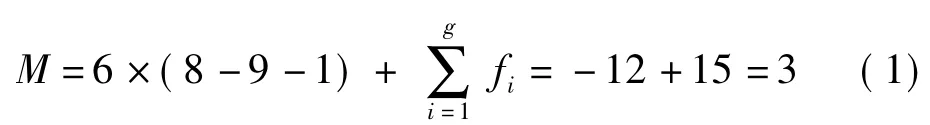
由式(1)可以看出，由于有平行四边形支链，直线驱动型并联机器人只有3个方向的平动自由度。

2 误差分析与模型的建立

2.1 几何误差定义

为了建立直线驱动型并联机器人的误差运动学模型，定义图3所示空间坐标系中的简化结构图。设定并联机器人基坐标系OXYZ原点建立在静平台等边三角形△A1A2A3的中心O点处，XY平面与3个伺服电动机转动副理想轴线共面，X轴指向第1条支链与静平台底面的交点处，Z轴方向与静平面垂直向下，过渡坐标系由坐标系{O}绕着Z轴旋转αi=2π/3(1－i)(i=1，2，3)得到。将过渡坐标系{Oi}的原点从O点平移到Ai点，就得到了主动臂坐标系{Ai}，再将坐标系{Ai}绕着YAi轴旋转θi得到坐标系{A'i}，Z'Ai轴与支链i中电缸的中心轴线重合，X'Ai轴垂直于电缸中心轴线。坐标系{O'}固接在动平台上，X'Y'平面与各四边形从动臂与动平台铰接处球铰中心所构成的平面共面，X'指向第1条支链中从动臂下端连接轴上两球铰中心连线的中点处，过渡坐标系{O'i}由坐标系{O'}绕着Z'轴旋转βi得到。

影响并联机器人位置精度有动态误差和静态误差［13－16］，动态误差通常包括机器人本身各部件在重力下的变形、温度对关节间运动副的间隙影响和周围噪声的影响等，静态误差主要有零部件尺寸加工误差和装配定位误差;本文只分析静态误差对并联机器人末端位置精度的影响，即分析机器人关键零部件尺寸误差和装配定位误差。由于机器人3条支链对称分布，现以直线驱动型并联机器人的第i条支链为例，如图3所示。

图3 直线驱动型并联机器人支链i误差源简图Fig．3 Error sources scheme of the i th chain of linear driven parallel robot

OAi、BiCi、DiEi、FiO'i的几何尺寸分别为R、h、L、r，其加工误差分别为d Ri、d hi、d Li、d ri;装配误差为:电缸与静平台安装接触点Ai在静平台的均布安装角为αi=(i－1)2π/3(i=1，2，3)，电缸与静平台底面夹角θi=38°，从动臂与动平台安装接触点Fi在动平台的均布安装角为βi=(i－1)2π/3(i=1，2，3)，对应装配误差为 dαi、dθi、dβi;Ci、Fi在杆件GiDi、HiEi的定位尺寸为e1i和e2i，对应装配误差为d e1i和d e2i。所以，直线驱动型并联机构静态误差源共有30项。

2.2 误差模型的建立

考虑到在3条支链中，电缸滑块与动平台之间的距离为平行四边形从动杆的杆长，所以以杆长约束建立关系式为

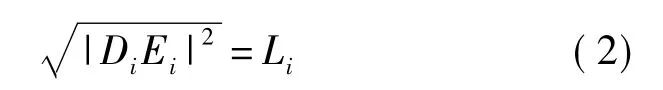
式中 Li——第i条支链中从动杆杆长

假设在并联机器人固定坐标系OXYZ中，Di点的坐标为(xDi，yDi，zDi)，Ei点的坐标为(xEi，yEi，zEi)，则式(2)可整理为

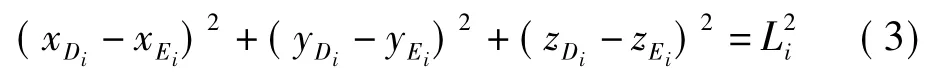
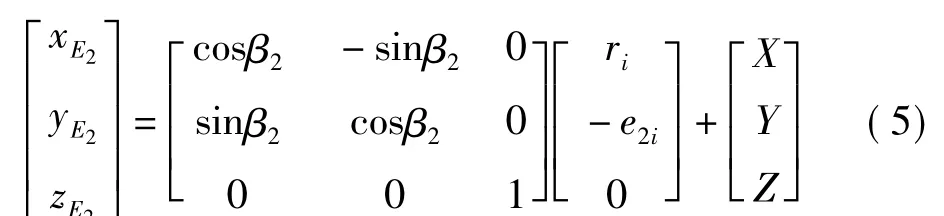
将式(4)和式(5)代入式(3)可得

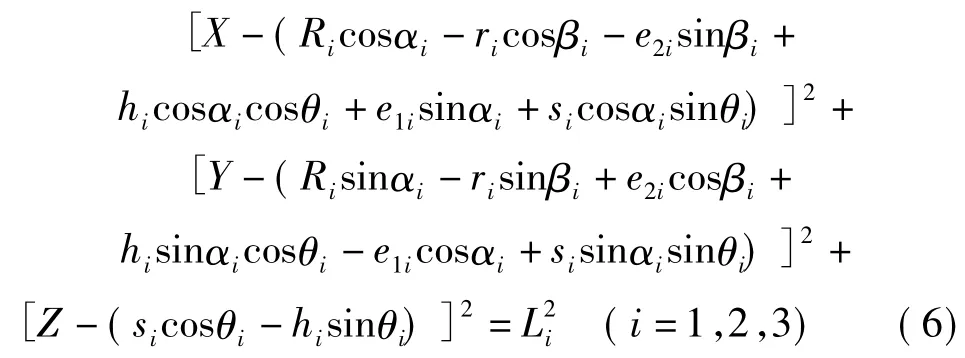
将式(6)简写为

根据式(7)，推算并联机器人正运动学问题时，除机器人结构参数集合p(p={Ri，ri，hi，e1i，e2i，αi，θi，βi，Li})为已知外，3个滑块的位置 m(m=［s1s2s3］)也为已知，机器人正向运动学模型可以表示为:q=f(m，p)，运用Matlab中solve函数可以求解出相应的动平台质心坐标 q(q=［x y z］T);在推算并联机器人逆运动学时，已知动平台质心坐标q和机器人结构参数集合p，逆运动学模型表示为:m=f－1(q，p)，通过约束条件: 388.429≤si≤688.429，利用Matlab中solve函数可得到滑块在电缸导轨上距离上端s1、s2、s3的唯一解。

对式(7)进行微分得

将式(8)简化为

式中 ε——动平台质心位置误差

δpi——机器人3条支链中零部件加工过程中的尺寸误差、驱动误差和装配误差在内的各项几何误差源的集合

Ci——与具体机械结构相关的位置误差系数矩阵

M'——直线驱动型并联机器人的逆雅可比矩阵J－1，与并联机器人位置及结构参数有关

若并联机器人处于奇异位置时，|J－1|=0，该方程没有研究意义。因为此时动平台处于奇异位置，在这种情况下，机构的实际自由度不再与理论自由度相等，即存在2种情况:①机构丧失了应有的自由度。②机构获得了额外的自由度。机构自由度的丧失意味着机构某种功能的丧失;机构获得额外的自由度则意味着即使锁定所有的驱动输入，机构在外力的作用下仍能运动，导致机构失控;当|J－1|≠0时，并联机器人处于非奇异位置，式(9)可以表示为

式(10)为直线驱动型并联机器人的误差映射函数，从式(10)可以看出，影响并联机器人动平台末端位置精度的误差源共有30项。

3 误差灵敏度分析

3.1 误差灵敏度模型建立

由于影响直线驱动型并联机器人动平台末端位置精度的误差源共有30项，对其逐一进行误差辨识相当复杂和繁琐，所以，在此建立灵敏度模型来分析各个误差源对动平台末端位置精度的影响［17－20］，并定义全局灵敏度指标，根据全局灵敏度指标值来筛选对动平台位置精度影响较大的误差源进行辨识。在建立灵敏度模型之前，先作2个假设:①式(9)中δpi的所有误差元素在统计学上是独立的，即它们之间的协方差为零。②所有误差元素都服从标准正态分布，即它们均值为零。根据2个假设和式(10)，可以得出

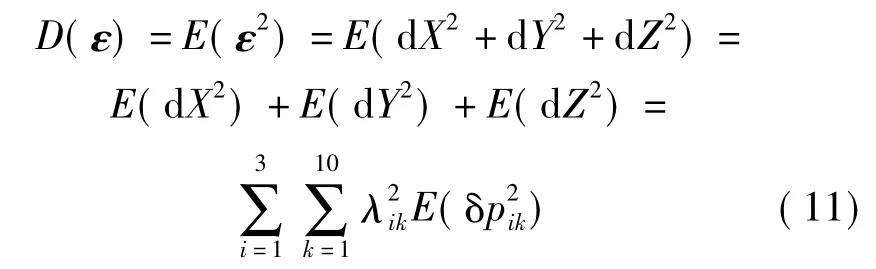
式中 λik——λi中第k个元素

δpik——δpi中第k个元素

其中

又因为直线驱动型并联机器人中3条支链呈120°对称分布，可以认为各条支链中同类的几何误差具有相同的数字特征，于是有

其中

式中 ωk——δ关于δpk的灵敏系数

ωk表征由δpk各误差源的单位标准差所引起动平台质心位置误差ε的标准差，又注意到λik随着机器人的位置变化而变化，所以用其在整个任务空间中的全域均值作为灵敏度评价指标，该指标可表示为

3.2 误差灵敏度分析

利用式(14)对直线驱动型并联机器人进行误差灵敏度分析，取并联机器人任务空间为600×200的圆柱体，并联机器人主要部件参数如表1所示。

表1 直线驱动型机器人主要部件参数Tab．1 Main parameters of linear driven robot

图4 灵敏度直方图Fig．4 Histogram of sensitivity

由图4可以看出，电缸与静平台底面安装夹角θ和3条支链在静平台上的分布角度α对整个工作空间内机器人动平台末端执行器定位精度影响最大，其次是电缸滑块的驱动s和平行四边形从动杆杆长L对末端执行器定位精度较大，对末端执行器定位精度影响稍大的是静平台半径R、动平台半径r和从动杆在动平台上的分布角度β，对末端执行器定位精度影响最小的是平行四边形从动杆分别与滑块和动平台接触处的定位尺寸e1、e2和滑块高度h;为此，在进行参数误差辨识时，将不考虑定位尺寸e1、e2和h的误差对机器人末端执行器位置精度的影响。

为了验证定位尺寸e1、e2和滑块高度h确实对末端位置精度影响不大，利用蒙特卡洛模拟法计算末端位置误差在不同高度上的分布规律，利用Matlab中randn函数随机产生均值为零的参数误差，其中，线性误差的标准差为0.01 mm，角度误差的标准差为0.02mm/m;分未考虑和考虑定位尺寸e1、e2和滑块高度h 2种情况，在每种情况下，在任务空间中分别取上、下2个平面，利用Matlab进行50次的模拟误差仿真，仿真结果如图5所示。

由分布图可以看出，随着工作平面到静平台距离的增大，相应工作平面的位置误差也随之增大;通过对比可以看出，2种情况下不同平面的位置误差分布图基本上是吻合的，所以灵敏度系数小的误差源对位置误差影响极小，基本可以忽略。因此只需要进行21项误差参数的辨识，就能有效地补偿直线驱动型并联机器人的位置误差。

4 实验验证

为验证上述所得结论对直线驱动型并联机器人精度标定的有效性和可行性，对并联机器人进行测量。实验所用测试平台如图6所示，测量工具是FARO公司的激光跟踪仪 Vantage(测试精度为(16+0.8)μm/m)，并用相应的辅助装夹设备来实时测量动平台中心的位置。在直线驱动型并联机器人理论工作空间中选取一些测量点，通过位置逆解解出这些点的电缸滑块位置，控制机器人运动到所选取点处，用激光跟踪仪测量其在激光跟踪仪坐标系下的空间坐标，限于篇幅，选取部分点的理论坐标和实测坐标如表2所示。

由误差灵敏度分析得，只需要进行21项误差参数的辨识，就能有效地补偿机器人的标定精度。这里选用遗传算法对其进行参数辨识，设任意2个测量点在机器人正解模型下的坐标分别为ri和rj，在激光跟踪仪坐标下的坐标为Ri和Rj，为了避免标定测量过程中机器人坐标系与测量装置坐标系之间转换带来的误差，采用相对位置替代绝对位置，所以定义残差

图5 不同平面下的位置误差分布Fig．5 Distribution maps of position error within different planes

图6 机器人标定测量现场Fig．6 Scene of test equipment

选定遗传算法的适应度函数为

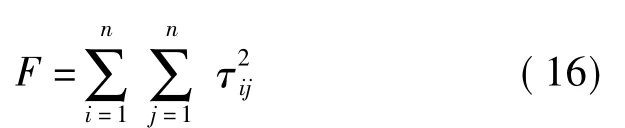
表2 机器人理论坐标和激光跟踪仪测量坐标Tab．2 Theoretical coordinates and measured coordinates mm

续表2 mm

表3 各项误差近似解Tab．3 Approximate solution of errors

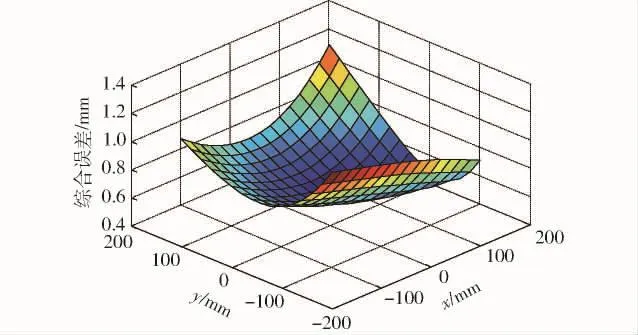
图7 z=959.070mm平面标定前动平台末端位置综合误差Fig．7 End position volume errors ofmoving platform of z=959.070mm plane before calibration

图8 z=959.070mm平面标定后动平台末端位置综合误差Fig．8 End position volume errors ofmoving platform of z=959.070mm plane after calibration

5 结论

(1)根据直线驱动型并联机器人几何结构模型和运动学模型，利用解析法建立动平台末端操作空间与关节空间之间的误差映射模型。

(2)在误差灵敏度模型的基础上，依据全域灵敏度评价指标，提出了一种误差源筛选方案，筛选影响位置精度的主要误差源，利用蒙特卡洛法进行随机模拟实验仿真，发现筛选前后动平台位置误差基本一致，验证了全域灵敏度评价指标的正确性。

(3)以激光跟踪仪为测量工具，对筛选后的主要误差源进行辨识，并修正并联机构的运动学模型，补偿后的平均综合误差为0.261 7mm，与补偿前的平均综合误差0.782 7mm相比，机器人的位置精度显著提高，验证了依据全域灵敏度指标所提出的误差源筛选方案对简化误差源和提高误差辨识效率是可行和有效的。

1 VISCHER P，CLAVEL R．Kinematic calibration of the parallel Delta robot［J］．Robotica，1998，6(2):207－218．

2 VEITSCHEGGER W K，WU C H．Robot calibration and compensation［J］．IEEE Journal of Robotics and Automation，1988，4(6):643－656．

3 DEBLAISE D，MAUR P．Effective geometrical calibration of a Delta parallel robot used in neurosurgery［C］∥IEEE/RSJ International Conference on Intelligent Robots and Systems，2005:1313－1318．

4 RENAUD P，ANDREFF N，MARQUET F，et al．Vision-based kinematic calibration of a H4 parallel mechanism［C］∥2003 International Conference on Robotics and Automation，2003，1:1191－1196．

5 RENAUD P，ANDREFFN，LAVEST JM，et al．Simplifying the kinematic calibration of parallelmechanisms using vision-based metrology［J］．IEEE Transaction on Robotics，2006，22(1):12－22．

6 GROTJAHN M，DAEMIM，HEIMANN B．Friction and rigid body identification of robot dynamics［J］．International Journal of Solids and Structures，2001，38(10):1889－1902．

7 MARTINELIA，TOMATISN．Simultaneous localization and odometry calibration formobile robot［C］∥Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems，2003:1499－1504．

8 RAUF A，PERVEZ A，UCHIYAMA M．Experimental results on kinematic calibration of parallel manipulators using pose measurement device［J］．IEEE Transactions on Robotics，2006，22(2):379－384．

9 MARCO A，STEVEN D．An analyticalmethod to eliminate the redundant parameters in robot calibration［C］∥Proceedings of IEEE International Conference on Robotics and Automation，2000:3609－3615．

10 KHALILM，GAUTIERM．Identifiable parameters and optimum configurations for robots calibration［J］．Robotica，1991，9(1): 63－70．

11 唐国宝，黄田．Delta并联机构精度标定方法研究［J］．机械工程学报，2003，39(8):55－60．TANG Guobao，HUANG Tian．Research on precision calibration method of Delta parallel mechanism［J］．Chinese Journal of Mechanical Engineering，2003，39(8):55－60．(in Chinese)

12 张文昌，梅江平，刘艺，等．基于激光跟踪仪的Delta并联机构运动学误差标定［J］．天津大学学报，2013，46(3):257－262．ZHANGWenchang，MEI Jiangping，LIU Yi，et al．Kinematic calibration error of Delta parallelmechanism based on laser tracker［J］．Journal of Tianjin University，2013，46(3):257－262．(in Chinese)

13 马晓丽，马履中，周兆忠．新型4自由度并联机构的运动学建模与分析［J］．农业机械学报，2006，37(3):100－104．MA Xiaoli，MA Lüzhong，ZHOU Zhaozhong．Kinematicsmodeling and analysis of a 4-DOF parallelmechanism［J］．Transactions of the Chinese Society for Agricultural Machinery，2006，37(3):100－104．(in Chinese)

14 VERL A，BOYE T，POTT A．Measurement pose selection and calibration forecast for manipulators with complex kinematic structures［J］．CIRP Annals Manafacturing Technology，2008，57:425－428．

15 马晓丽，陈艾华，陈晓英，等．虚拟轴工作台机构的误差分析和补偿［J］．农业机械学报，2007，38(11):123－128．MA Xiaoli，CHEN Aihua，CHEN Xiaoying，et al．Error analysis and compensation of a parallel mechanism for virtual-axial worktable［J］．Transactions of the Chinese Society for Agricultural Machinery，2007，38(11):123－128．(in Chinese)

16 谭兴强，张键，谢志江．风洞6_PUS并联支撑机器人运动误差建模与补偿［J/OL］．农业机械学报，2014，45(4):334－340．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?file_no=20140453＆flag=1．DOI:10．6041/j．issn．1000-1298．2014．04．053．TAN Xingqiang，ZHANG Jian，XIE Zhijiang．Motion error modeling and compensating for 6_PUS parallel robot of wind tunnel support system［J］．Transactions of the Chinese Society for Agricultural Machinery，2014，45(4):334－340．(in Chinese)

17 CHEN Yuzhen，XIE Fugui，LIU Xinjun，etal．Errormodeling and sensitivity analysis of a parallel robotwith SCARAmotions［J］．Chinese Journal of Mechanical Engineering，2014，27(4):693－702．

18 李晓丹．3-SPR机构的误差灵敏度分析［J］．机床与液压，2015，15(8):44－46．LIXiaodan．Error sensitivity analysis of 3-SPR mechanism［J］．Machine Tool and Hydraulic，2015，15(8):44－46．(in Chinese)

19 洪振宇，梅江平，赵学满，等．可重构混联机械手——TriVariant的误差建模与灵敏度分析［J］．机械工程学报，2006，42(12):65－69．HONG Zhenyu，MEIJiangping，ZHAOXueman，etal．Errormodeling and sensitivity analysis of reconfigurable hybrid robotmodule TriVariant［J］．Chinese Journal of Mechanical Engineering，2006，42(12):65－69．(in Chinese)

20 FAN K C，WANG H，ZHAO JW，et al．Sensitivity analysis of the 3-PRS parallel kinematic spindle platform of a serial-parallel machine tool［J］．International Journal of Machine Tools and Manufacture，2003，43(15):1561－1569．

Error Modeling and Sensitivity Analysis of Linear Driven Parallel Robot

YU Jin1YUWei1WU Chaoyu1CHENG Min1QIAN Xiaowu2
(1．The State Key Laboratory of Mechanical Transmissions，Chongqing University，Chongqing 400044，China 2．Department of Mathematics，Physics and Chemistry，Zhenjiang College，Zhenjiang 212002，China)

In order to improve the position precision of moving platform end effector of linear driven parallel robot，based on structure and kinematic model of parallel mechanism，the dimension errors，driving errors and assembly errors of parallel robotwhich influenced accuracy of themoving platform end effector were analyzed，the non-linearmapping from the actuated variables in joint space to the pose of the end-effector in operating space was established with analytic method．On the basis of the sensitivity errormodel，an error source selection scheme was proposed according to the global sensitivity evaluation index，which was defined to evaluate the error source on the position error of themoving platform in given workspace，and themain error sources that affected the location accuracy was selected．Itwas found that the position error of the moving platform was basically the same between all error sources and selected error sources by randomly simulating the dimension errors，driving errors and assembly errors of the parallel robotwith Monte Carlomethod，which verified the consistency of the evaluation index．By taking laser tracker asmeasurement tool，the position precision of themoving platform end effector of the parallel mechanism was improved remarkably after detecting the selected main errors of the parallel robot and calibrating the forward kinematic model，which verified the validity and feasibility of the error source selection scheme and reduced the complexity and computation of the error parameter identification．Ithad greatly important guidance to the error compensation of the complex structure．

parallel robot;errormodeling;global sensitivity;error source selection scheme

TP242

A

1000-1298(2017)07-0383-08

2017-04-21

2017-05-26

国家自然科学基金项目(51375507)和重庆市基础与前沿研究计划项目(cstc2016jcyjA0253)

于今(1964—)，男，副教授，主要从事流体传动与智能控制、机器人研究，E-mail:915638526@qq．com

10．6041/j．issn．1000-1298．2017．07．049