六自由度模块化机器人手臂奇异构型分析

李宪华 盛 蕊 张雷刚 宋 韬 张 军

(1．安徽理工大学机械工程学院，淮南232001;2．上海市智能制造及机器人重点实验室，上海200444)

六自由度模块化机器人手臂奇异构型分析

李宪华1盛 蕊1张雷刚1宋 韬2张 军1

(1．安徽理工大学机械工程学院，淮南232001;2．上海市智能制造及机器人重点实验室，上海200444)

对六自由度模块化机器人手臂工作空间内的奇异构型进行了分析。首先搭建模块化机器人手臂系统，并采用DH法对其进行结构建模，得到正运动学方程;其次，结合机器人手臂的正运动学方程，采用基于机器人连杆速度的方法构造其雅可比矩阵，再基于雅可比矩阵求解机械臂出现奇异状态的所有构型情况，得到所有奇异点并分别给出相应的手臂构型;最后，基于可操作度灵活性指标和最小奇异值灵活性指标应用Robotics工具箱对机械臂的奇异情况进行仿真分析，并考察机械臂处于奇异位型时末端参考点的可操作度椭球情况。仿真结果表明该机械臂共有3种奇异情况，验证了上述机械臂奇异位型分析的正确性，为后续模块化机械臂的轨迹规划研究和奇异点规避研究奠定了基础。

模块化机械臂;雅可比矩阵;灵活性;奇异构型;机器人工具箱

引言

模块化机械臂是由一系列具有不同功能尺寸特征与一定装配关系的关节、连杆和执行器等模块组成，各模块间通过机械和电气连接能构成不同工作空间、自由度的机械臂结构。机械臂在执行任务时需要保证其运动可靠性和稳定性，因此在保证机械臂的工作特性和运动精度的前提下，需通过合理的算法回避机械臂的奇异位型，故对机械臂的奇异性进行分析至关重要。机械臂的奇异位型主要有边界奇异位型和内部奇异位型［1］，边界奇异位型出现在机械臂工作空间边界，内部奇异位型则是由于2个及2个以上关节轴线重合造成的。当机械臂处于奇异位型时，会出现自由度缺失、灵活性变差、雅可比矩阵降秩等情况，因此研究机械臂奇异性对提高其作业性能具有重要意义。

对于机械臂而言，奇异性是机械臂的重要运动学特性［2］。国内外学者对机械臂的奇异性研究做出了很大贡献，机械臂的奇异位型分析理论主要有代数理论［3］、旋量理论［4］和线几何理论［5－6］。李诚等［7］采用微分变换法求得装校机器人的雅克比矩阵并对其进行奇异性分析，得到该机器人的奇异情况;张新等［8］以反恐排爆机器人五自由度机械臂为研究对象，求得其雅克比矩阵并对其进行奇异位型和工作空间分析;史士财等［9］应用一种相关旋量抑制的方法分析了一种7自由度机械臂，得到了该机械臂的奇异位型及其几何特征;BOHIGAS等［10］提出了一种基于数值计算的分析机构奇异位型的方法，并对平面连杆机构和并联机构进行奇异性分析; NOKLEBY［11］针对7自由度加拿大臂2做了奇异性分析，得到机械臂处于奇异位型的所有情况; CHENG等［12］分析了一种6自由度PUMA机器人的奇异性，并得到该机器人的奇异位型。近年来笔者所在课题组针对模块化机械臂做了大量的研究工作，笔者针对模块化机器人双臂进行了研究，完成了其运动学正解及逆解的解算和基于VC++编制运动学算法验证程序［13］。

本文针对课题组构建的六自由度模块化机器人手臂，首先采用DH法对其进行结构建模，得到正运动学方程;其次，采用一种基于机器人连杆速度的方法构造其雅可比矩阵，然后基于雅可比矩阵求解机械臂出现奇异状态的所有构型情况，并给出其相应的物理构型;最后，基于可操作度指标和最小奇异值指标，应用Robotics工具箱对机械臂的奇异位型进行仿真分析。

1 机器人手臂运动学

1.1 手臂系统构建

本文研究的机器人手臂采用德国Amtec公司的PowerCube模块构成，机器人的双臂结构完全一致，均由6个关节模块和1个手爪模块组成，各个模块间是由课题组设计和加工的连接件连接而成。机器人手臂系统的构建过程如图1所示，由于机器人2个手臂完全一致，现以其中一条手臂为研究对象。将手臂的末端坐标系原点选在关节4、5、6的交点处，即不考虑手爪的长度(参数d6)。机械臂常用的坐标系建立方法有 DH 法则［14－15］和螺旋理论［16］2种，其中DH法则应用较为广泛，故本文采用DH法则来描述机械臂的结构参数，进而建立其连杆坐标系，手臂模型以及完整的坐标系如图2所示，机器人手臂DH参数如表1所示。

图1 机器人手臂系统的构建过程Fig．1 Construct process ofmanipulator

图2 手臂模型以及手臂坐标系Fig．2 Model and coordinate frame ofmanipulator

表1 机器人手臂DH参数Tab．1 DH parameter ofmanipulator

1.2 运动学分析

在确定手臂的结构参数后，仅关节角为变量，可以求得手臂正运动学方程为

式中 θi——关节变量

p——末端参考点相对基坐标系的位置向量

［n o a］——末端参考点相对基坐标系的姿态矩阵

2 机器人手臂奇异构型分析

2.1 雅可比矩阵

机器人的雅可比矩阵定义为从关节空间向操作空间运动速度传递的广义传动比V［1］，即

J(q)——雅可比矩阵

雅可比矩阵可用于判别机器人的奇异位型，它是描述机器人手臂特征的重要参量，通常雅可比矩阵的求解方法有矢量积法［17］、微分变换法［1］、力和力矩递推法［1］。上述雅可比矩阵的求解方法中含有大量的矩阵乘法运算，计算量大且表达式冗长，本文则采用一种基于机器人连杆速度的简便方法构造雅可比矩阵［18］，由于本文机器人手臂只含有转动关节，故只给出转动关节的雅可比矩阵计算表达式为

其中

pe——机械臂末端参考点位置向量

zi－1——关节i－1的轴线方向向量

pi－1——连杆i－1的位置向量

通过式(3)～(6)可得出本文机器人手臂的雅可比矩阵形式为

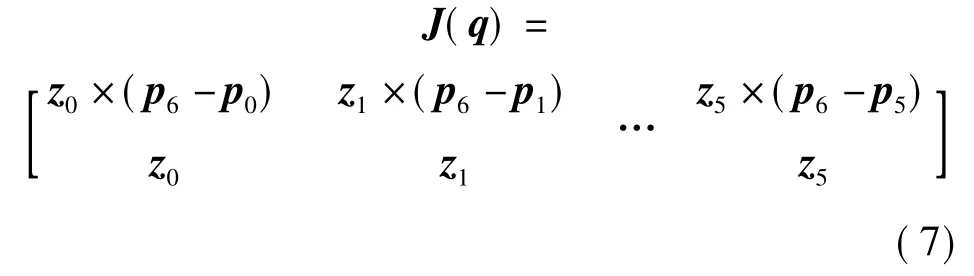
结合机器人手臂的正运动学方程分别求得z0、z1、z2、z3、z4、z5以及p0、p1、p2、p3、p4、p5、p6，由于手臂的末端坐标系原点在关节4、5、6的交点处，故有p4= p5=p6，且向量p6－p3和向量z3平行，为了便于分析将式(7)中矩阵进行分块，即

其中ci表示cosθi，si表示sinθi，由于篇幅原因J22的具体表达式不再给出。

2.2 机器人手臂奇异位型分析

机器人手臂奇异位型的出现由其自身结构造成，与描述其运动学坐标系的选取无关，故文中将手臂的末端坐标系原点选在关节4、5、6的交点处对手臂奇异性分析没有影响。机械臂出现奇异位型相当于机械臂丧失了一个或多个自由度，数学上用雅可比矩阵行列式是否为零来判断，即求出雅可比矩阵行列式为零的点即为机器人手臂的奇异点。由于式(8)中的J12为3×3阶零矩阵，故机器人手臂雅可比矩阵为下三角矩阵，存在关系

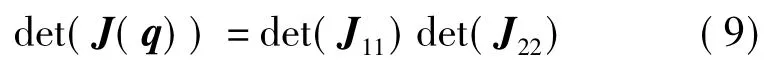
通过式(9)将机器人手臂的奇异性进行解耦分析，则有det(J11)=0或者det(J22)=0。

当det(J11)=0时得到

当det(J22)=0时得到

由上述分析可以得到机器人手臂奇异的3种情况:

(1)当cosθ2=0时，在机械臂的关节运动范围内有θ2=±π/2时，det(J11)=0，此时雅可比矩阵不可逆，机器人手臂出现奇异位型，关节速度会趋向于无穷大，此时机器人手臂的位姿如图3所示。

(2)当sinθ3=0时，在机械臂的关节运动范围内有θ3=0时，det(J11)=0，机器人手臂出现奇异位型，关节速度会趋向于无穷大，关节2和4轴线重合，手臂为伸直状态，此时手臂处于肘部奇异状态，机器人手臂的位姿如图4所示。

图3 θ2=±π/2时的奇异位型Fig．3 Singular configuration whenθ2=±π/2

图4 θ3=0时的奇异位型Fig．4 Singular configuration whenθ3=0

(3)当sinθ5=0时，在机械臂的关节运动范围内有θ5=0时，det(J22)=0，机器人手臂出现奇异位型，此时关节4和6轴线重合，手臂处于腕部奇异状态，机器人手臂的位姿如图5所示。

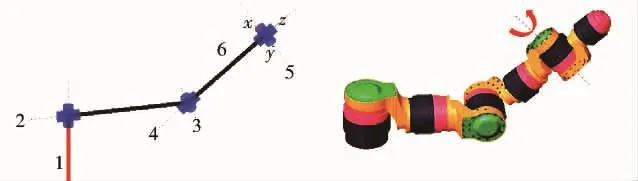
图5 θ5=0时的奇异位型Fig．5 Singular configuration whenθ5=0

2.3 灵活性指标

2.3.1 可操作度

机器人手臂灵活性是机器人运动学的重点研究内容，可操作度、条件数和最小奇异值是较为经典的3个机械臂灵活性评价指标，本文采用可操作度和最小奇异值衡量手臂的灵活性。YOSHIKAWA［19］将雅可比矩阵与其转置之积的行列式定义为可操作度指标

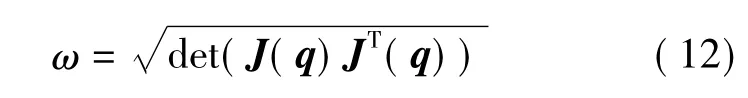
式中 ω——可操作度

它是指机械臂在各个方向上运动能力的综合量度，可以来表示机器人的整体灵活性。

在可操作度的定义基础上，YOSHIKAWA进一步提出了可操作度椭球，如图6所示，该椭球在几何层面上更加清晰、形象地对机器人的运动灵活性进行了阐述，将机器人的关节速度定义为一个单位球［20］，即

通过雅可比矩阵J(q)映射为任务空间的一个椭球，即

椭球各轴长的方向与(J(q)JT(q))－1的特征向量一致，各轴长等于其特征值平方根的倒数，也等于J(q)的奇异值。

图6 可操作度椭球Fig．6 Manipulability ellipsoid

显然，当雅可比矩阵为方阵时，ω=|det(J(q))|。当手臂处于奇异位型时，其雅可比矩阵降秩，即rand(J(q))小于其自由度，ω=0，手臂的可操作性为0，其对应的可操作度椭球在某个方向上的轴长也趋于0，退化为一平面。

2.3.2 最小奇异值

雅可比矩阵的最小奇异值表征了机械臂末端参考点的最难运动方向，可以作为衡量手臂构型与奇异位型接近程度的指标。KLEIN等［21］提出了将最小奇异值作为一种灵活性能指标来评估机械臂的灵活性。根据矩阵的奇异值分解理论，对雅可比矩阵J(q)进行奇异值分解［22］

式中U∈Rm×n，V∈Rn×n，σ1，σ2，…，σm为J(q)的奇异值。对角矩阵Σ和雅可比矩阵具有相同的秩，即rank(Σ)=rank(J(q))，且有

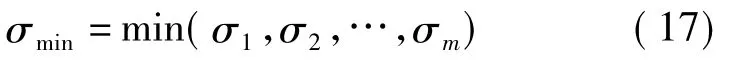
当手臂处于奇异位型附近时，会有σmin→0，手臂在该方向上最难运动，手臂灵活性变差。

3 手臂奇异性仿真分析

上文分析了六自由度模块化机器人手臂的奇异情况，共有3种奇异类型，为对上述分析进行验证，现应用Robotics工具箱对手臂的奇异性进行仿真分析。

(1)θ2=±π/2时。选定其他关节角度，让关节2角度在其运动范围内变化，即q=(0，θ2，π/6，0，π/6，0)，得到最小奇异值、可操作度和雅可比矩阵的秩随关节2角度变化曲线如图7所示，q=(0，π/2，π/6，0，π/6，0)和q=(0，－π/2，π/6，0，π/6，0)时机器人手臂末端参考点的可操作度椭球如图8所示。

图7 关节2角度与奇异值、可操作度、雅可比矩阵秩的关系Fig．7 Relationships between the second joint angle and singular value，manipulability and rank of Jacobianmatrix

图8 θ2=±π/2时的可操作度椭球Fig．8 Manipulability ellipsoid whenθ2=±π/2

(2)θ3=0时。选定其他关节角度为定值，使关节3角度在其运动范围内取值，即q=(0，π/6，θ3，0，π/6，0)，得到最小奇异值、可操作度和雅可比矩阵的秩随关节3角度的变化曲线如图9所示，q= (0，π/6，0，0，π/6，0)时机器人手臂末端参考点的可操作度椭球如图10所示。

(3)θ5=0时。选定其他关节角度为定值，使关节5角度在其运动范围内取值，即 q=(0，π/6，π/6，0，θ5，0)，得到最小奇异值、可操作度和雅可比矩阵的秩随关节5角度变化曲线如图11所示，q= (0，π/6，π/6，0，0，0)时机器人手臂末端参考点的可操作度椭球如图12所示。

由上述仿真结果可看出，机器人手臂的奇异位型共有3种，而且当出现上述3种情况的组合时，机器人手臂也处于奇异位型。机器人手臂在第1种奇异位型时，即θ2=±π/2，如图7、8所示，雅可比矩阵的最小奇异值在θ2=±π/2时发生突变，最小奇异值趋于0，此时手臂末端参考点的可操作度为0，雅可比矩阵也在θ2=±π/2处出现降秩，手臂末端参考点的位置可操作椭球在θ2=±π/2处退化为一个平面，说明θ2=±π/2是手臂的一个奇异位型;机器人手臂在第2种奇异位型时，即θ3=0，如图9、10所示，雅可比矩阵的最小奇异值在θ3=0时发生突变，且此时雅可比矩阵最小奇异值以及手臂末端参考点的可操作度均为0，雅可比矩阵也在θ3=0处出现降秩，手臂末端参考点的位置可操作度椭球在θ3=0处退化成为一个平面，说明θ3=0是手臂的一个奇异位型;同理机器人手臂在第3种奇异位型时，即θ5=0，如图11、12所示，可知θ5=0也是手臂的一个奇异位型。仿真结果进一步验证了文中求得的机器人手臂奇异位型的正确性。

图9 关节3角度与奇异值、可操作度、雅可比矩阵秩关系Fig．9 Relationships between the third joint angle and singular value，manipulability and rank of Jacobian matrix

图10 θ3=0时的可操作度椭球Fig．10 Manipulability ellipsoid whenθ3=0

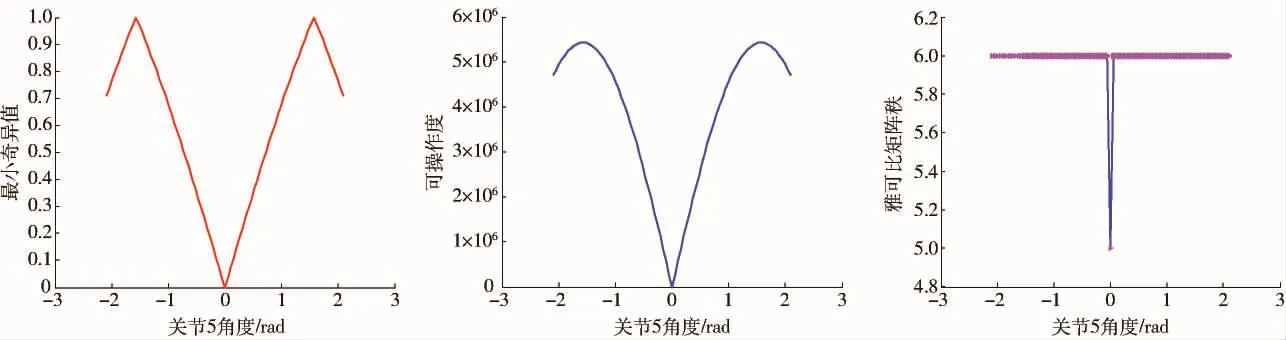
图11 关节5角度与奇异值、可操作度、雅克比矩阵秩关系Fig．11 Relationships between the fifth joint angle and singular value，manipulability and rank of Jacobian matrix

图12 θ5=0时的可操作度椭球Fig．12 Manipulability ellipsoid whenθ5=0

4 结束语

针对课题组构建的六自由度模块化机器人手臂构型，求解其运动学方程和雅可比矩阵，分析得到了机器人手臂处于奇异位型时的所有情况，并基于可操作度指标和最小奇异值指标应用Robotics工具箱对机械臂的奇异情况进行仿真分析，仿真结果验证了本文机械臂奇异位型分析的正确性。通过分析求解和仿真结果发现:该构型的机器人手臂与PUMA构型机器人的奇异情况不完全一样，该构型的机器人手臂共有3种奇异位型，分别是θ2=±π/2、θ3=0和θ5=0，手臂在这3种位型时，机器人手臂处于奇异状态，此时手臂的雅可比矩阵最小奇异值以及手臂末端参考点的可操作度均趋于0，手臂末端参考点的位置可操作度椭球也退化为一平面，出现自由度缺失、灵活性变差、雅可比矩阵降秩等情况。

1 熊有伦，唐立辛，丁汉，等．机器人技术基础［M］．武汉:华中科技大学出版社，2008．

2 梁喜凤，王永维．番茄收获机械手奇异性分析与处理［J］．农业工程学报，2006，22(1):85－88．LIANG Xifeng，WANG Yongwei．Analysis and treatment of singularity for a tomato harvestingmanipulator［J］．Transactions of the CSAE，2006，22(1):85－88．(in Chinese)

3 MERLET JP．A formal-numerical approach for robust in-workspace singularity detection［J］．IEEE Transactions on Robotics，2007，23(3):393－402．

4 吕永军．六关节串联机器人机构奇异位形研究［D］．沈阳:中国科学院研究生院(沈阳计算技术研究所)，2016．LYongjun．Research on singularity of 6-joint series robotmechanism［D］．Shenyang:Graduate School of Chinese Academy of Sciences(Shenyang Institute of Computing Technology)，2016．(in Chinese)

5 PENNE R，SMET E，KLOSIEWICZ P．A short note on point singularities for robotmanipulators［J］．Journal of Intelligent and Robotic Systems，2011，62(2):205－216．

6 杰姆．基于格拉斯曼-凯莱代数的机器人运动学奇异性分析［D］．武汉:华中科技大学，2014．JIM．Analysis of singularities condition of robots manipulators based on Glassman-Cayley algebra［D］．Wuhan:Huazhong University of Science and Technology，2014．(in Chinese)

7 李诚，谢志江，倪卫，等．六自由度装校机器人雅可比矩阵的建立及奇异性分析［J］．中国机械工程，2012，23(10):1165－1169．LICheng，XIE Zhijiang，NIWei，et al．Establishmentof Jacobianmatrix and singularity analysis of a 6-DOF installing-calibrating robot［J］．China Mechanical Engineering，2012，23(10):1165－1169．(in Chinese)

8 张新，马郡，马汶锴，等．排爆机器人机械臂奇异位形及工作空间分析［J］．天津工业大学学报，2015，34(5):37－42．ZHANG Xin，MA Jun，MA Wenkai，et al．Analysis of singular configuration and workspace of EOD robot's arm［J］．Journal of Tianjin Polytechnic University，2015，34(5):37－42．(in Chinese)

9 史士财，尹斌，蒋再男．一种七自由度冗余机械臂的奇异构形特征分析［J］．机械与电子，2014(10):67－70．SHIShicai，YIN Bin，JIANG Zainan．Features analysis of singular configurations ofa 7-DOF redundantmanipulator［J］．Machinery and Electronics，2014(10):67－70．(in Chinese)

10 BOHIGASO，ZLATANOV D，ROSL，etal．A generalmethod for the numerical computation ofmanipulator singularity sets［J］．IEEE Transactions on Robotics，2014，30(2):340－351．

11 NOKLEBY SB．Singularity analysis of the Canadarm2［J］．Mechanism＆Machine Theory，2007，42(4):442－454．

12 CHENG F T，HOUR T L，SUN Y Y，et al．Study and resolution of singularities for a 6-DOF PUMA manipulator［J］．IEEE Transactions on Systems，Man and Cybernetics-Part B:Cybernetics，1997，27(2):332－343．

13 李宪华，郭永存，张军，等．模块化六自由度机械臂逆运动学解算与验证［J/OL］．农业机械学报，2013，44(4):246－251．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?file_no=20130443＆flag=1．DOI:10．6041/j．issn．1000-1298．2013．04．043．LIXianhua，GUO Yongcun，ZHANG Jun，et al．Inverse kinematics solution and verification ofmodular 6-DOF manipulator［J/ OL］．Transactions of the Chinese Society for Agricultural Machinery，2013，44(4):246－251．(in Chinese)

14 杨新刚，黄玉美，杨文栋，等．基于可操作性的串联机器人相对传动比优化［J］．农业机械学报，2009，40(8):209－213．YANG Xin'gang，HUANG Yumei，YANG Wendong，et al．Relative proportion of serial robot transmission ratios optimization based on manipulability［J］．Transactions of the Chinese Society for Agricultural Machinery，2009，40(8):209－213．(in Chinese)

15 张永贵，黄玉美，高峰．基于遗传算法的机器人运动学参数误差识别［J］．农业机械学报，2008，39(9):153－157．ZHANG Yonggui，HUANG Yumei，GAO Feng．Robotic kinematics parameters error identification based on genetic algorithm［J］．Transactions of the Chinese Society for Agricultural Machinery，2008，39(9):153－157．(in Chinese)

16 焦有宙，丁攀，赵大旭．温室3P3R机械臂系统动力学建模与分析［J/OL］．农业机械学报，2012，43(5):179－183．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20120531＆journal_id=jcsam．DOI:10．6041/j．issn．1000-1298．2012．05．031．JIAO Youzhou，DING Pan，ZHAO Daxu．Dynamicmodeling and analysis for3P3R universalmanipulator in greenhouse［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2012，43(5):179－183．(in Chinese)

17 张鹏程，张铁．基于矢量积法的六自由度工业机器人雅可比矩阵求解及奇异位形的分析［J］．机械设计与制造，2011(8): 152－154．ZHANG Pengcheng，ZHANG Tie．Analysis on solution of6D of robot Jacobianmatrix and singularity configuration based on vector productmethod［J］．Machinery Design and Manufacture，2011(8):152－154．(in Chinese)

18 BRUNO S，LORENZO S，LUIGI V，et al．Robotics:modelling，planning and control［M］．London:Springer-Verlag London Limited，2010:105－113．

19 YOSHIKAWA T．Manipulability of roboticmechanisms［J］．International Journal of Robotics Research，1985，4(2):3－9．

20 谢碧云，赵京．机器人运动灵活性问题研究概述［J］．机械科学与技术，2011，30(8):1386－1393．XIE Biyun，ZHAO Jing．Advances in robotic kinematic dexterity and indices［J］．Mechanical Science and Technology，2011，30(8):1386－1393．(in Chinese)

21 KLEIN C A，BLAHO B E．Dexterity measures for the design and control of kinematically redundant manipulators［J］．International Journal of Robotics Research，1987，6(2):72－83．

22 PATEL S，SOBH T．Manipulator performance measures—a comprehensive literature survey［J］．Journal of Intelligent and Robotic Systems，2015，77(3－4):547－570．

Singular Configuration Analysis of 6-DOF Modular Manipulator

LIXianhua1SHENG Rui1ZHANG Leigang1SONG Tao2ZHANG Jun1
(1．School of Mechanical Engineering，Anhui University of Science and Technology，Huainan 232001，China 2．Shanghai Key Laboratory of IntelligentManufacturing and Robotics，Shanghai200444，China)

Aimed at 6-DOF modular manipulator，singular configurations was analyzed within its workspace．Firstly，modularmanipulator system was constructed，and the forward kinematicsmodel was conducted by using the DH method．Secondly，combining the kinematics equation，the Jacobian matrix was constructed by usingmethod based on link speed ofmanipulator，and all the singular states of the manipulator was solved through the method of singular decomposition，all the singular points within its workspace were acquired and the corresponding configurationswere shown．Lastly，simulation analysis of manipulator with singular configurationswas completed based on themanipulability flexible index and the minimum singular value flexible index by means of the robotics toolbox，changing of themanipulability，the smallest singular value and the Jacobian matrix rank of manipulator were shown during each joint rotting within its range，and the manipulability ellipsoid of end reference point of manipulator was explored when manipulator was in singular configuration．The simulation results showed that the manipulator had three singular states within its workspace，and the manipulability and the minimum singular value were tended to zero，the Jacobian matrix was rank-reduced and the position manipulability ellipsoid of end reference point of manipulator was reduced to a plane when manipulator was in each singular states above．Simulation results verified the correctness of the singularity analysis，and laid a foundation for subsequent trajectory planning research and singularity avoidance research of modular manipulator．

modularmanipulator;Jacobian matrix;flexibility;singular configuration;Robotics toolbox

TP241

A

1000-1298(2017)07-0376-07

2016-11-21

2017-01-13

国家高技术研究发展计划(863计划)项目(2007AA041604)、安徽省高校自然科学研究重点项目(KJ2016A200)和安徽省科技重大专项(16030901012)

李宪华(1980—)，男，副教授，主要从事机器人技术研究，E-mail:xhli01@163．com

10．6041/j．issn．1000-1298．2017．07．048