Tripod并联机器人工作空间完全解析与实验验证
2017-07-31牟家旺吴超宇钱小吾
牟家旺 于 今 吴超宇 程 敏,2 钱小吾
(1.重庆大学机械传动国家重点实验室,重庆400044;2.浙江大学流体动力与机电系统国家重点实验室,杭州310027; 3.镇江高等专科学校数理化工系,镇江212002)
Tripod并联机器人工作空间完全解析与实验验证
牟家旺1于 今1吴超宇1程 敏1,2钱小吾3
(1.重庆大学机械传动国家重点实验室,重庆400044;2.浙江大学流体动力与机电系统国家重点实验室,杭州310027; 3.镇江高等专科学校数理化工系,镇江212002)
针对Tripod并联机器人工作空间一般用数值搜索方法研究,难以给出边界曲面准确表达的问题,提出一种曲面扫略分析与机械结构形位分析结合的方法来解析Tripod并联机器人的工作空间。以正逆解的算法为基础,得到并联机器人各单开链扫略空间范围及其包络曲面表达式,用三维软件布尔运算得出各支链公共的工作空间,在考虑虎克铰约束和杆件干涉的情况下,再依据机械结构形位分析得到机器人实际工作空间及边界曲面表达式,并对工作空间的奇异性进行了分析。通过三坐标测量仪器测出实际的工作空间与理论分析解析出来的空间进行对比来验证解析方法的正确性,从而为机器人机械结构参数设计和工作空间计算奠定基础。
并联机器人;曲面扫略分析;形位分析;工作空间;边界曲面表达式
引言
自从CLAVEL[1]提出Delta三自由度并联机器人以来,由于其具有更好的承载能力、运动精度和刚度而被广泛应用于工程中,也一直是国际上研究的热点。国内外研究的少自由度并联机器人多为转动副的Delta机器人,而Tripod并联机器人是以平移副代替转动副,在大尺寸结构参数的情况下,电机的负载转动惯量更小,有更好的应用前景。在把并联机器人应用于工程实际过程中,首先需要解决的问题就是确定一个已知机械结构参数的机器人工作空间。现有Tripod并联机器人并联空间的研究很多,大多采用数值法中的三维搜索法[2-3]或者用计算机辅助模拟法确定工作空间[4]。GOSSELIN[5]则利用圆弧相交的方法来确定6自由度并联机器人的定姿态工作空间,并给出了工作空间的3维表示,此法以求工作空间的边界为目的,且可以直接计算工作空间的体积。FICHER[6]采用固定6个位姿参数中的3个姿态参数和一个位置参数,而变换其他2个参数研究了6自由度并联机器人的工作空间。MASORY等[7]同时考虑到各关节转角的约束、各杆长的约束和机构各构件的干涉来确定并联机器人的工作空间,且采用数值积分的方法计算工作空间的体积,比较接近实际。采用数值法虽然直观,但是存在计算时间长,边界曲面存在误差,不能求解完全的解。LI等[8]提出一种综合考虑空间利用率和全局空间灵活度的工作空间优化方法,其核心的工作空间求解还是采用数值搜索法。
相对于解析法,数值法求解无法获得准确的边界曲面方程,只能有直观的认识,无法准确获取空间尺寸与机械结构尺寸的数学关系,从而无法根据空间需求定向地调整机械结构参数[9-11]。
本文采用曲面扫略分析结合机械结构形位约束的数形方法,以正逆解[12-14]的算法为基础,分析方程特点得到并联机器人单开链子空间范围,求解边界曲面的解析表达式,从而得出空间尺寸与机械结构尺寸的关系,为以空间尺寸为标准的设计提供理论依据。
1 Tripod机器人运动学模型建立
Tripod并联机构由上、下2个等边三角形平台及3条完全相同的支链组成,如图1所示,每条支链都由1个平移运动的电缸(平移副P)和1个平行四边形机构组成,电缸与上面静平台以一个固定角度固连,电缸滑块与平行四边形机构以虎克铰(U副)连接,平行四边形与下面的动平台也以虎克铰(U副)连接。由空间自由度计算公式可知,此机构有3个自由度,动平台只能实现3个方向的平动。根据运动副的连接顺序,Tripod机器人又叫3-PUU型并联机器人。
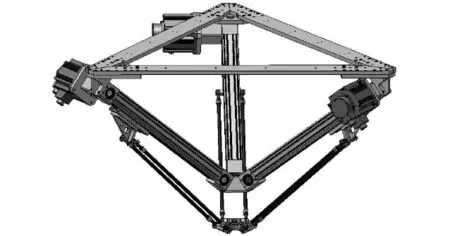
图1 并联机器人三维模型Fig.1 3-Dmodel of parallelmechanism
在静平台上固连基坐标OXYZ,坐标原点位于静平台中心,X轴过点A1,Y轴平行于A2A3。OA1到A1B、OA2到A2B、OA3到A3B的转角分别为α1、β1、θ1,静平台为边长为L的等边三角形,动平台为边长为R的等边三角形,平行四边形杆件机构简化为一个杆,如图2中CiDi长度为M。滑块距离Ai点的距离为滑块的滑行距离si;根据杆长约束建立方程式

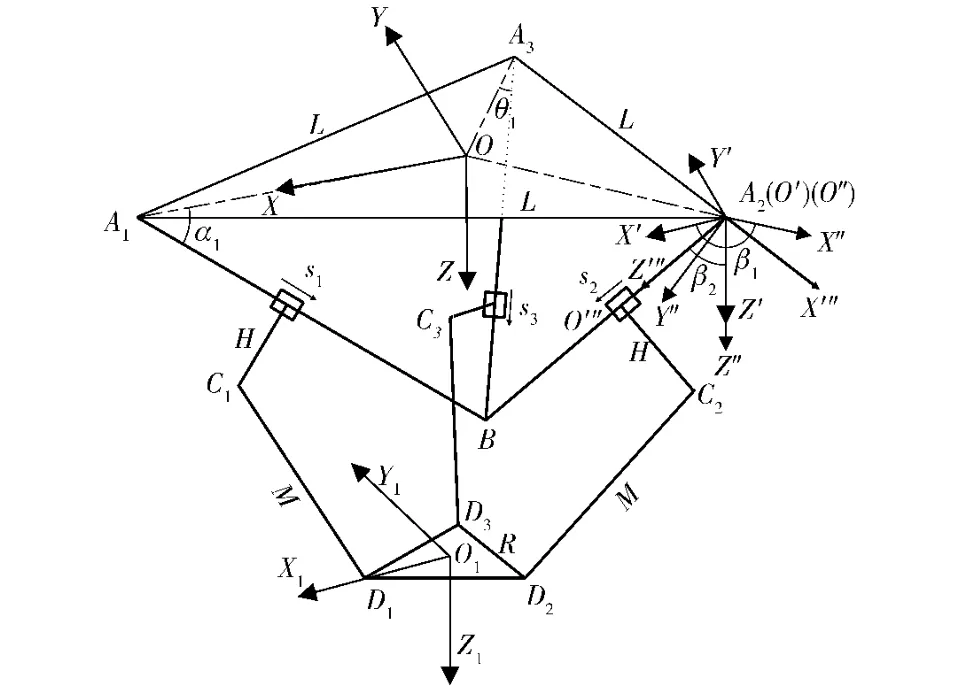
图2 并联机器人运动简图Fig.2 Kinematic diagram of parallelmechanism
设坐标系OXYZ中Ci、Di的坐标为(xi,yi,zi)、(Xi,Yi,Zi),则式(1)可整理为

以第2条支链为例,平移坐标系OXYZ原点到A2得到坐标系O'X'Y'Z',绕Z'轴逆时针旋转坐标系O'X'Y'Z',角度为β1,使X轴平行于OA2得到坐标系O″X″Y″Z″,再绕Y″轴顺时针旋转坐标系O″X″Y″Z″,角度为 β2,使 Z″轴平行于电缸方向得到坐标系OXYZ。则在坐标系OXYZ下C2点的坐标为(H,0,s2),则在坐标系OXYZ下的坐标(x2,y2,z2)为
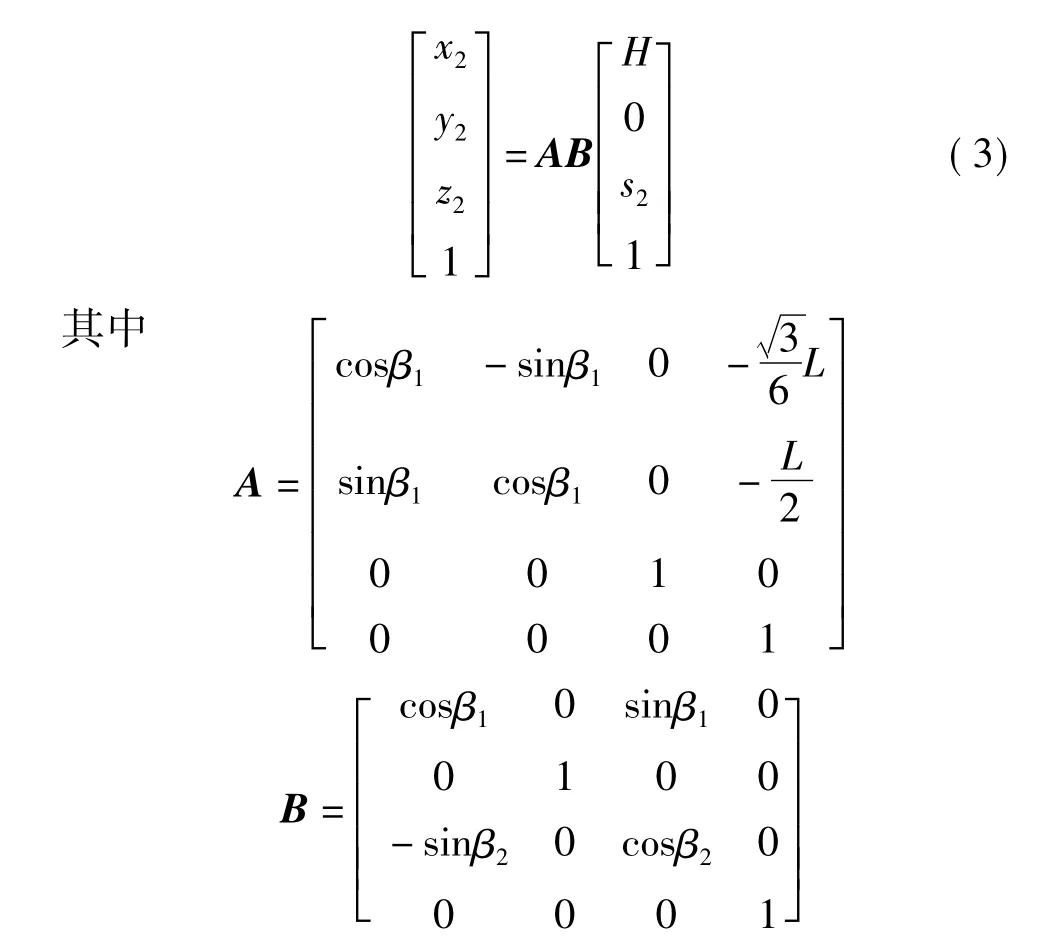
在动平台上固连坐标系O1X1Y1Z1,坐标原点位于动平台中心点 O1,X1轴过点 D1,Y1轴平行于D2D3。在坐标系OXYZ中,令坐标系O1X1Y1Z1的原点坐标为(X,Y,Z),研究机器人的工作空间即研究动平台中心点,即O1(X,Y,Z)可到达的运动空间,则D2坐标为

在已知电缸行程 s1、s2、s3情况下,3个未知数3个方程联立方程式(5)~(7)得到动平台中心坐标(X,Y,Z),即为3-PUU机器人运动学正解;在已知动平台中心坐标(X,Y,Z)的情况下联立方程式(5)~(7)得到每个电缸的行程si,即为3-PUU机器人运动学逆解。
2 工作空间解析
观察式(5)~(7)为空间球面方程形式,令所描述的球面分别表示为ψi(i=1,2,3)。球心的坐标在机械结构参数L、R、H、αi、βi、θi为定值时,球面ψi只随着si的变化而移动。当电缸的行程si变化时,圆心的轨迹分别为
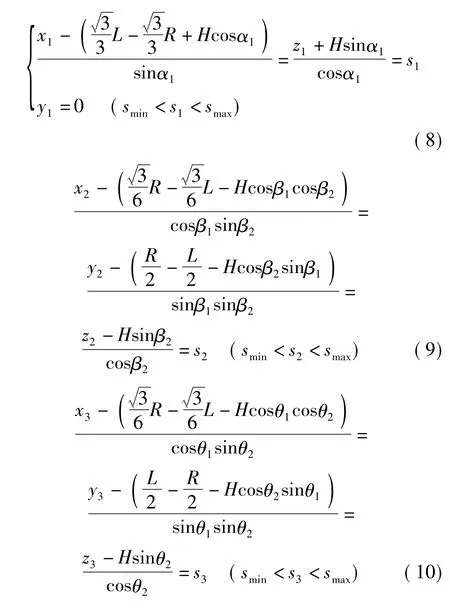
上述3条轨迹分别记作Li(i=1,2,3)。当电缸的行程si变化时,球面ψi的圆心沿着空间直线Li连续移动,球面ψi扫过的三维空间就是动平台中心O1在支链i约束下的变化范围,如图3所示。

图3 单开链子空间边界截面图Fig.3 Sectional view of single-open-chain sub-space boundary
根据球面在空间中的扫略过程分析可知,每个支链空间的外边界面可分为3部分,前后两端各有2个半球面,中间为空间圆柱面,圆柱面轴线过Li,如图4所示。
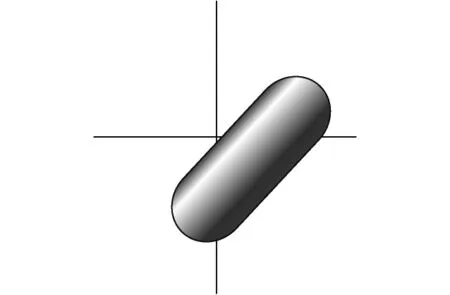
图4 单开链子空间三维图Fig.4 3-D model of single-open-chain sub-space
当给定si变化范围时,两端球面的方程已知,则求解单支链运动空间边界曲面方程的问题简化为求中间空间圆柱面方程的问题。由于此空间圆柱面的准线和母线方程都容易求得,联立2个方程,则可以求出空间任意方向圆柱面的表达式。由下文可知,圆柱面不是空间的边界面,所以方程结果不在文中详细描述。
根据上述分析,并代入并联机器人机械结构参数:L=1 300.41 mm,R=103.923 mm,M=610 mm,H=98.5 mm,α1=-52°,β1=-120°,β2=-52°,θ1=120°,θ2=-52°。当3个支链约束下确定的3个三维空间求交集时,得到的公共空间就是动平台中心O1在不考虑其他约束条件下的理想可达空间,如图5所示。

图5 理想可达空间三视图Fig.5 Three views of ideal reachable space
结合机器人的机械结构形位特征,对上述可达空间进行形位分析。当式(5)~(7)中si取最小值时,得到的3个球面分别为3个支链中一条支链滑块在上极限位置,另外2个支链滑块任意运动得到的面。根据实际情况中电缸和平行四边形连杆机构的安装位置约束可知,动平台中心O1只可能出现在以这3个球面为上边界面的以下空间中,否则平行四边形机构将会和电缸发生干涉,所以在上述动平台O1理想可达空间中切去这3个球体的空间,得到考虑了杆件干涉、不考虑虎克铰限制的可达空间,如图6所示。

图6 工作空间三视图Fig.6 Three views ofworkspace
空间由上下各3个球面包络出来,黑色上凹面是式(5)取si为最小值时确定的球面,黑色下凸面是式(5)取si为最大值时确定的球面,红色上凹面是式(6)取si为最小值时确定的球面,红色下凸面是式(6)取si为最大值时确定的球面,黄色上凹面是式(7)取si为最小值时确定的球面,黄色下凸面是式(7)取si为最大值时确定的球面。
3 虎克铰约束分析
研究的Tripod机器人虎克铰结构如图7所示。

图7 虎克铰结构图Fig.7 Diagram of Hooke hinge structure
与传统的虎克铰不同,所设计的虎克铰第1个自由度的旋转副U1在物理上没有角度限制,可以360°的旋转,旋转轴为U1第2个自由度的旋转副U2有角度限制,旋转轴为U1,建立虎克铰的简化模型,如图8所示。
过轴线U1,垂直于U2轴线创建平面2,其法向量设为n1;过U2旋转副的对称中心,平行于轴线U2并垂直于轴线U1创建平面1,其法向量设为n2。以第2条支链为例,由于旋转副U1没有结构上的角度限制,所以虎克铰的约束主要来自于旋转副U2,由结构特点可知,旋转副U2的旋转范围关于平面1对称,设杆件C2D2与平面1的夹角为γ21,所以与平面1的法向量n1的夹角为90°-γ21,根据几何关系可知


图8 虎克铰角度说明图Fig.8 Diagram of Hooke hinge angle
根据实际的结构限制可知,-40°≤γ21≤40°,由于n1为平面1的法向量,可得

由前文论述可知

将式(3)、(4)、(12)、(13)代入式(11)中,并代入机器人结构参数,可得

整理可得
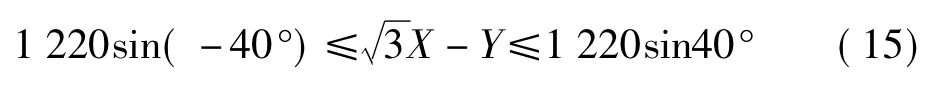
同样的方法可得到其他2条支链的方程,支链1为
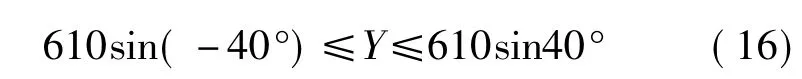
支链3为

将上述表达式(15)~(17)表示成几何描述即为工作空间必须为表达式所表示的6个平面包围的范围内,如图9所示。

图9 虎克铰约束的范围Fig.9 Range of Hooke hinge constraint
由图9可知,用扫略分析结合机械结构形位分析方法得到的工作空间(图6)都在虎克铰约束范围内,满足虎克铰约束条件。
4 奇异性分析
奇异位形是当机构进入某种临界状态时所具有的特定形态,在这种临界状态下,机构的实际自由度不再与理论自由度相等,即存在两种情况:一是机构丧失了应有的自由度;二是机构获得了额外的自由度。机构自由度的丧失意味着机构某种功能的丧失;机构获得额外的自由度则意味着即使锁定所有的驱动输入,机构在外力的作用下仍能运动,导致机构失控。一般而言,机构奇异位形研究的内涵体现在2个方面:对于确定的机构,找出它的所有奇异位形以及如何有效地避免机构奇异位形。分析式(5)~(7)可知,其描述的是动平台坐标O1(X,Y,Z)与电缸位移S(s1,s2,s3)的关系,可表示为

式中 Q——动平台位置矢量
S——平移驱动副的位置矢量
对零矢量方程(18)中各分量Q、S、O分别对时间求导,可得
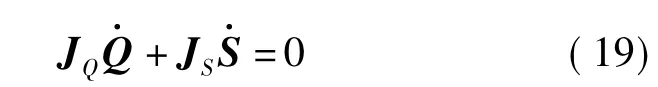
其中
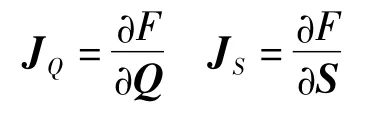
由式(19)可知当det(JS)=0时,存在非零向量Q产生零矢量S,当det(JQ)=0时,存在非零向量S产生零矢量Q,第1种情况即为逆运动学奇异,给定一个指定的运动方向,却得不到驱动的平移量,这一类情况多发生于机器人工作空间边界处,所有图5所示的工作空间边界(其中包括单支链工作空间球体交界处)都是奇异位置,第2种情况即为正运动学奇异,给定驱动的平移量,末端动平台位置矢量不变,即无论驱动如何运动,动平台始终不变。由于这一类奇异位置会在工作空间内部,所以本文主要讨论这一类奇异位置。令时,。将式(5)~(7)对时间t进行求导,得到


即J是该并联机构的雅可比矩阵,当det(J)= 0时,表明机构位于奇异位,机构丧失一个自由度。求|J|=0,经过化简得到
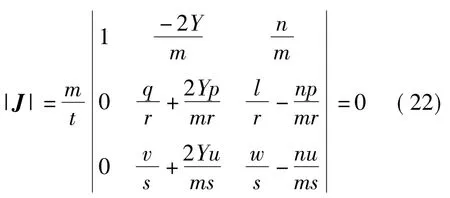
由此得到

则qw=lv,pw=ul,pv=qu,然后代入方程(5)~(7)。得到当X=Y=Z=0时,|J|=0,也就是静平台的原点位置时,此时上下平台半径相等,三分支平行,机构位于奇异位置。由于Z=0,所以静平台与动平台在同一平面。但此位置实际上是机构不能达到的位置,所以工作空间除边界外内部不存在奇异位置。
5 样机工作空间扫描实验验证
为验证所提出的工作空间解析方法的正确性,进行了样机工作空间扫描实验。实验所用3-PUU并联机器人如图10所示,并联机器人机械结构参数与上述理论分析的机器人参数相同。采用FARO公司激光跟踪仪 Vantage(测试精度为(16+ 0.8)μm/m)和相应的辅助装夹设备来实时测量动平台中心的位置。

图10 测试设备现场图Fig.10 Scene diagram of test equipment
空间扫描方法具体如下:3-PUU机器人在手动模式下,选定一个Z平面进行扫描,扫描的轨迹为先从(X,Y)=(0,0)的点开始,X单轴运动到负极限位置,再将Y轴单轴在X、Z坐标固定的条件下从负极限运动到正极限位置,激光跟踪仪以Y轴运动5 mm为一个步长,记录一个点的坐标位置。当Y轴运动到正极限位置后,X坐标增加10mm,再重复上述Y轴操作,完成整个Z平面的扫描。测试现场图如图10所示。由于难以对机器人完整的工作空间进行直接对比,为了验证理论计算的结果,任意选取2个Z切面来进行平面比较,比较理论计算和实验测试得到的空间切面是否相同,验证理论结果的正确性。由理论分析结果可知,工作空间上下两部分的切面形状存在较大的差异,所以在上下两部分分别选取2个平面进行验证,一个平面为Z=750 mm所对应的平面;另一个平面为Z=1 000mm所对应的平面;将理论分析空间切面和实验测试空间切面的数据放一起对比,如图11、12所示。

图11 Z=750mm理论和测试数据对比Fig.11 Comparison of theory and test data of Z=750mm plane

图12 Z=1 000mm理论和测试数据对比Fig.12 Comparison of theory and test data of Z=1 000mm plane
如图11、12所示,2个切面的大小、形状基本一致。为了证明理论和实际测试数据吻合,以每个测试边界点为圆心画圆,使每个圆与理论数据曲线相切,记录每个圆的半径。以测试点的X轴坐标为横坐标,以对应圆的半径为纵坐标,作出理论与测试数据分析图,如图13所示。
由图13可知,2个平面的误差范围绝对值最大为3.337mm,都小于5mm,即小于一个步长。考虑到测试数据由于机器人安装误差、控制器运动控制误差和测试误差的细微影响,上述误差在允许范围内,可以证明理论和实际测试数据吻合,理论分析结果正确。

图13 Z=1 000mm与Z=750mm平面误差Fig.13 Error analysis of data of Z=1 000mm and Z=750mm plane
6 结论
(1)建立Tripod并联机器人运动学模型,并得出了机器人运动学正逆解。
(2)在正逆解的基础上,提出了一种Tripod并联机器人工作空间解析方法:通过分析曲面扫略范围结合机械结构形位约束得到工作空间包络曲面的数学模表达,从而根据曲面表达式建立工作空间重要尺寸参数和机械结构参数之间的数学关系,从而获得了精确的机器人三维工作空间表达式,解决了常用数值分析法所不能解决的问题。
(3)考虑了虎克铰的限制,并做了理论分析,得出分析所得工作空间满足虎克铰的限制;并做了空间奇异性分析,没有奇异点出现。
(4)最后,用实验测试的空间三维扫描数据和理论计算工作空间进行对比,结果一致,证明了所提出的工作空间解析方法的正确性,从而为机器人工作空间计算、机械结构参数设计等提供了理论依据。
1 CLAVEL R.Une nouvelle structure demanipulateur parallèle pour la robotiquelégère[J].APII.,1989,23:501-519.
2 QIAN Y U,WANG Q,CHEN G,et al.Workspace and singularity analysis of3/3-RRRS parallel[J].Journal of Theoretical and Applied Information Technology,2013,48(3):1423-1429.
3 REZAEIA,AKBARZADEH A,NIA PM,et al.Position,Jacobian and workspace analysis of a3-PSP spatial parallelmanipulator[J].Robotics and Computer-Integrated Manufacturing,2013,29(4):158-173.
4 YU M L,WANG JR,LI J,et al.Kinematics analysis of exoskeletons rehabilitation robot based on ADAMS[C]∥Advanced Materials Research,2012,479:2333-2338.
5 GOSSELIN CM.Determination of theworkspace of6-DOF parallelmanipulators[J].ASME Journal of Mechanical Design,1990,112(3):331-336.
6 FICHER E F.A Stewart-platform based manipulator:general theory and practical construction[J].International Journal of Robotics Research,1986,5(2):157-182.
7 MASORY O,WANG J.Workspace evaluation of Stewart platforms[J].Advanced Robotics,1994,9(4):443-461.
8 LIY,XU Q.A new approach to the architecture optimization of a general3-PUU translational parallelmanipulator[J].Journal of Intelligent&Robotic Systems,2006,46(1):59-72.
9 HARADA T,DONG K,ITOIGAWA T.Design optimization of active scanning probe using parallel link mechanism[J].International Journal of Precision Engineering and Manufacturing,2012,13(8):1387-1394.
10 RUGBANIA,SCHREVE K.Modeling and analysis of the geometrical errors of a parallel manipulator micro-CMM[C]∥International Precision Assembly Seminar,2012:105-117.
11 陈根良,王皓,来新民,等.基于广义坐标形式牛顿-欧拉方法的空间并联机构动力学正问题分析[J].机械工程学报,2009,45(7):41-48.CHEN Genliang,WANGHao,LAIXinmin,etal.Workspace resolution andmechanism optimization on Delta parallelmechanism driven by prismatic pair[J].Chinese Journal of Mechanical Engineering,2009,45(7):41-48.(in Chinese)
12 ZHAO Y,QIU K,WANG S,et al.Inverse kinematics and rigid-body dynamics for a three rotational degrees of freedom parallelmanipulator[J].Robotics and Computer-Integrated Manufacturing,2015,31:40-50.
13 牛雪梅,高国琴,刘辛军,等.三自由度驱动冗余并联机构动力学建模与试验[J].农业工程学报,2013,29(16):31-41.NIU Xuemei,GAO Guoqin,LIU Xinjun,etal.Dynamicsmodeling and experiments of3-DOF parallelmechanism with actuation redundancy[J].Transactions of the CSAE,2013,29(16):31-41.(in Chinese)
14 张清华,张宪民.平面3-RRR柔性并联机器人残余振动主动控制[J/OL].农业机械学报,2013,44(2):232-237,266.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130242&flag=1.DOI:10.6041/j.issn.1000-1298.2013.02.042.ZHANG Qinghua,ZHANG Xianmin.Active residual vibration control of planar 3-RRR flexible parallel robots[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(2):232-237,266.(in Chinese)
15 黄田,汪劲松,WHITEHOUSE D J.Stewart并联机器人位置空间解析[J].中国科学(E辑),1998,28(2):136-145.HUANG Tian,WANG Jinsong,WHITEHOUSE D J.Workspace resolution on Stewart parallelmechanism[J].Science in China (Series E),1998,28(2):136-145.(in Chinese)
16 梅江平,高奔,谭杨,等.3-SPR并联机构运动学分析[J/OL].农业机械学报,2012,43(8):215-220.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20120839&flag=1.DOI:10.6041/j.issn.1000-1298.2012.08.039.MEIJiangping,GAO Ben,TAN Yang,et al.Kinematic analysis of 3-SPR parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2012,43(8):215-220.(in Chinese)
17 崔国华,周海栋,王南,等.基于Isight的3-UPS-S并联机器人机构多目标优化[J/OL].农业机械学报,2013,44(9):261-266.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130945&flag=1.DOI:10.6041/j.issn.1000-1298.2013.09.045.CUIGuohua,ZHOU Haidong,WANG Nan,et al.Multi-objective optimization of3-UPS-Sparallelmechanism based on Isight[J/ OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(9):261-266.(in Chinese)
18 LEE K M,SHAH D K.Dynamic analysis of a three degrees of freedom in parallel actuated manipulator[J].IEEE Journal of Robotics and Automation,1988,4(3):361-367.
19 张彦斌,张树乾,吴鑫.3-CRPa移动并联机构运动学分析与仿真[J/OL].农业机械学报,2012,43(7):200-205.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20120737&flag=1.DOI:10.6041/j.issn.1000-1298.2012.07.037.ZHANG Yanbin,ZHANG Shuqian,WU Xin.Kinematic analysis and simulation of 3-CRPa translational parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2012,43(7):200-205.(in Chinese)
20 冯李航,张为公,龚宗洋,等.Delta系列并联机器人研究进展与现状[J].机器人,2014,36(3):375-384.FENG Lihang,ZHANG Weigong,GONG Zongyang,et al.Developments of Delta-like parallel manipulators—a review[J].Robot,2014,36(3):375-384.(in Chinese)
21 高名旺,张宪民,刘晗.3-RRR高速并联机器人运动学设计与实验[J].机器人,2013,35(6):716-722.GAO Mingwang,ZHANG Xianmin,LIU Han.Experiment and kinematic design of 3-RRR parallel robot with high speed[J].Robot,2013,35(6):716-722.(in Chinese)
Workspace Resolution of Tripod Parallel Manipulator and Experimental Verification
MOU Jiawang1YU Jin1WU Chaoyu1CHENG Min1,2QIAN Xiaowu3
(1.The State Key Laboratory of Mechanical Transmissions,Chongqing University,Chongqing 400044,China 2.State Key Laboratory of Fluid Power and Mechatronic Systems,Zhejiang University,Hangzhou 310027,China 3.Department of Mathematics,Physics and Chemistry,Zhenjiang College,Zhenjiang 212002,China)
Aiming at the difficulty of using accurate analytical formulas to represent the Tripod parallel robotworkspace boundary surfaces,a method called surface-sweep analysis combined with the shape of mechanical structure analysis was proposed to give an accurate expression to the workspace of Tripod parallelmanipulator.On account of the Tripod parallel robot,the geometric model of the parallel robot was set up and the architecture of the parallel robot and the driving mode of the parallel robot were introduced.Based on the algorithm of forward and inverse kinematics solution,the scope of sweeping space and envelope surface expression of this sweeping space considering one of the robot parallel’s open chains were obtained.Then,the six envelope surfaceswere drawn in sequence and the overlap partof the six sweeping space was solved.In 3-D software,the public workspace can be obtained by using boolean operation algorithm.Then,under the consideration ofmechanical structure of shape analysis and physical constraints,the actual workspace and boundary surface expression of robot can be obtained.Furthermore,the singularity of the obtained workspace was analyzed.According to the comparison of workspacemeasured by the three coordinate measuring instrument and the workspace obtained by 3-D software,the validity of this analyticmethod was verified by using the error analysismethod,which layed foundation for the next step to figure out the influence ofmechanical parameters on the workspace and do some work on the size optimization of the parallel robot.
parallel robot;surface-sweep analysis;shape analysis;workspace;boundary surface expression
TP242
A
1000-1298(2017)07-0368-08
2016-10-31
2016-11-28
国家自然科学基金项目(51375507)、重庆市基础与前沿研究计划项目(cstc2016jcyjA0253)和流体传动与机电系统国家重点实验室开放基金项目(GZKF-201503)
牟家旺(1992—),男,博士生,主要从事智能控制、机器人与流体传动研究,E-mail:moujiawang@qq.com
于今(1964—),男,副教授,主要从事流体传动与智能控制、机器人研究,E-mail:yj93@cqu.edu.cn
10.6041/j.issn.1000-1298.2017.07.047
