沙障地表形态衍化数值模拟方法研究

孙 浩 刘晋浩 黄青青

(北京林业大学工学院，北京100083)

沙障地表形态衍化数值模拟方法研究

孙 浩 刘晋浩 黄青青

(北京林业大学工学院，北京100083)

提出了一个风沙相互作用数值模型，该模型以概率统计理论为基础，通过计算不同地表风速下沙粒的风蚀与沉积概率来实现风-沙相互作用过程，最后通过动网格技术，改变下边界节点坐标，实现沙床表面的起伏变化。数值计算与野外沙障凹坑的测量结果对比表明，沙障内地表形态的数值计算结果与实测地表形态较为接近，凹坑最低点位置向下风向一侧移动，误差最大位置为凹坑的最低点处，t=4 d时，平均绝对误差为17.86%，随着积沙增加，误差逐渐减小，t=8 d时，平均绝对误差为8.52%。所提模型无论从定性还是从定量上，都与野外测量结果较为一致，可以正确模拟沙障地表的发展过程。

沙障;地表过程;动网格;数值方法

引言

沙障在防风固沙工程中被大量应用并占有重要地位。一般认为，沙障可以有效降低近地表风速，抑制沙粒启动，削弱地表风沙流强度。科研人员对不同类型沙障的防风效能［1－4］、沙障周围流场特征［5－8］进行了大量的研究，而对沙障的衰退过程，目前研究还相对较少。一般认为，沙障方格内积沙是导致沙障失去固沙能力的主要原因。沙障的衰退过程即为沙障逐渐被沙掩埋的过程。沙障在铺设完成后，首先在沙障方格前沿开始产生积沙，并逐渐向纵深发展，上风侧的方格积沙量相对较高，下风向沙障内积沙较少，随着沙的淤积，沙障露出地表的高度逐渐降低，最终失去固沙能力，同时积沙饱和带也逐渐前移，当沙障内达到蚀积动态平衡时，沙粒不再沉积［9］。一种情况为沙障完全被沙掩埋，固沙带变成近乎于平坦地表;另一种情况为沙障形成稳定凹曲面，由于沙障后的涡流气动作用达到蚀积平衡，此时固沙带完全丧失阻沙能力。许多国内学者对不同尺寸的沙障内凹曲面进行研究，结果表明，1 m×1 m方格沙障容易形成稳定凹曲面，以凹坑深度与方格尺寸比值表示蚀积系数，在1/10～1/8之间［10－13］。稳定凹曲面的形成条件与风力、沙障材料及地表坡度密切相关，稳定凹曲面的蚀积系数也会发生相应变化［14］。

沙障凹曲面的发展是一个动态过程，目前对沙障的凹曲面发展速度、沙障衰退时间方面仍然研究不足，主要是野外环境较为复杂，同时需要长时间的监测工作。在风沙相互作用的研究中，数值计算是一个重要的研究方法，大量的研究表明，数值计算可以很好地描述风沙运动的瞬态形为，与实验结果较为接近，但当前的数值计算方法只能模拟短时间的流固两相运动过程［15－16］，对于沙障凹坑的形成过程这种大时间尺度问题的模拟，无论是欧拉-欧拉［17－18］还是欧拉-拉格朗日［19－22］双流体模型都无法满足要求。

为了对沙障地表发展过程这种大时间尺度的风沙运动进行模拟，本文基于概率理论对风沙相互作用数值模型进行研究，为沙障衰退过程及障内凹曲面形成预测提供方法，从而为工程治沙及沙障尺寸设计提供理论支撑。

1 数值方法

本文数值模型计算结构与传统两相流数值计算结构相同，由流体计算和沙体计算两部分构成，流体计算采用传统计算流体力学方法，沙体计算由本研究提出的模型进行计算。

1.1 沙相网格划分

在现有的两相流模拟中，气固两相之间的相互作用行为表示为气固两相之间的动量交换行为，在网格数量与颗粒数量都较多时，需要大量计算资源。而本研究为了实现大空间尺度的模拟，在模拟沙相时提出采用双重网格思想，原理如图1所示。

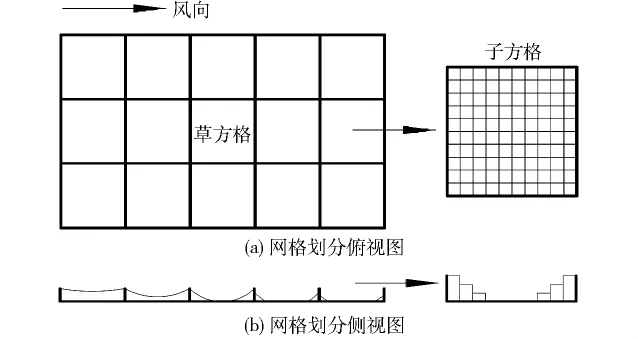
图1 沙相网格划分原理Fig．1 Principle of sand phasemeshing

将整个沙障地表看作二维平面，划分网格时首先按草方格尺寸划分网格，作为母网格，网格单元数量与沙障网格数量相等。再对母网格进行网格划分，生成子网格。首先将沙床表面进行粗糙网格划分，计算粗糙网格总沙量变化，然后对粗糙网格再次细化，计算母网格单元的积沙量在子网格单元的分布情况，最终计算子网格单元厚度，实现地表动态变化。

1.2 风沙两相耦合计算过程

风沙两相流计算主要包含气相计算和沙相计算，具体步骤为:①施加边界条件。对计算模型的气相和沙相的计算域施加边界条件，气相计算需要设置壁面类型、速度入口、时间步长等参数，沙相计算需要对沙粒物理参数、地表输沙量、时间步长及沙相模型相关参数等进行初始化。②风场计算。应用传统的流体计算理论对空气相进行计算，并获得下边界壁面剪力数据。③沙相计算。通过壁面剪力计算沙床表面每个子网格单元输沙率，进而计算整个草沙障输沙率，计算沙床沉降量分布和侵蚀量分布。④基于沙障间沙粒沉降概率模型计算每个子网格单元的沙粒沉降量，进而确定子单元网格厚度。⑤循环检测相邻子网格单元厚度，超过沙体坍塌临界角度时，子单元发生坍塌行为，修改子单元网格厚度。⑥采用动网格技术根据子单元厚度，调整下边界网格节点坐标，实现沙床表面动态变化，然后根据边界网格坐标变化，调整内部网格节点坐标。⑦判断程序终止时间，如果到达终止时间程序结束，否则返回。计算流程如图2所示。

1.3 风沙相互作用数值模型

将每个草方格内部看做一个母单元，草方格内部积沙和风蚀总量确定之后，计算沙障内部具体的风沙蚀积行为。草方格内风沙相互作用原理如图3所示。图中Qin为进入方格上空的总输沙率;a为进入方格区域内的来流风沙的进入概率;aQin为来流风沙影响方格内部沙床蚀积变化的输沙率;Qerosion/n为方格内子单元由于风蚀产生的平均起沙输沙率。

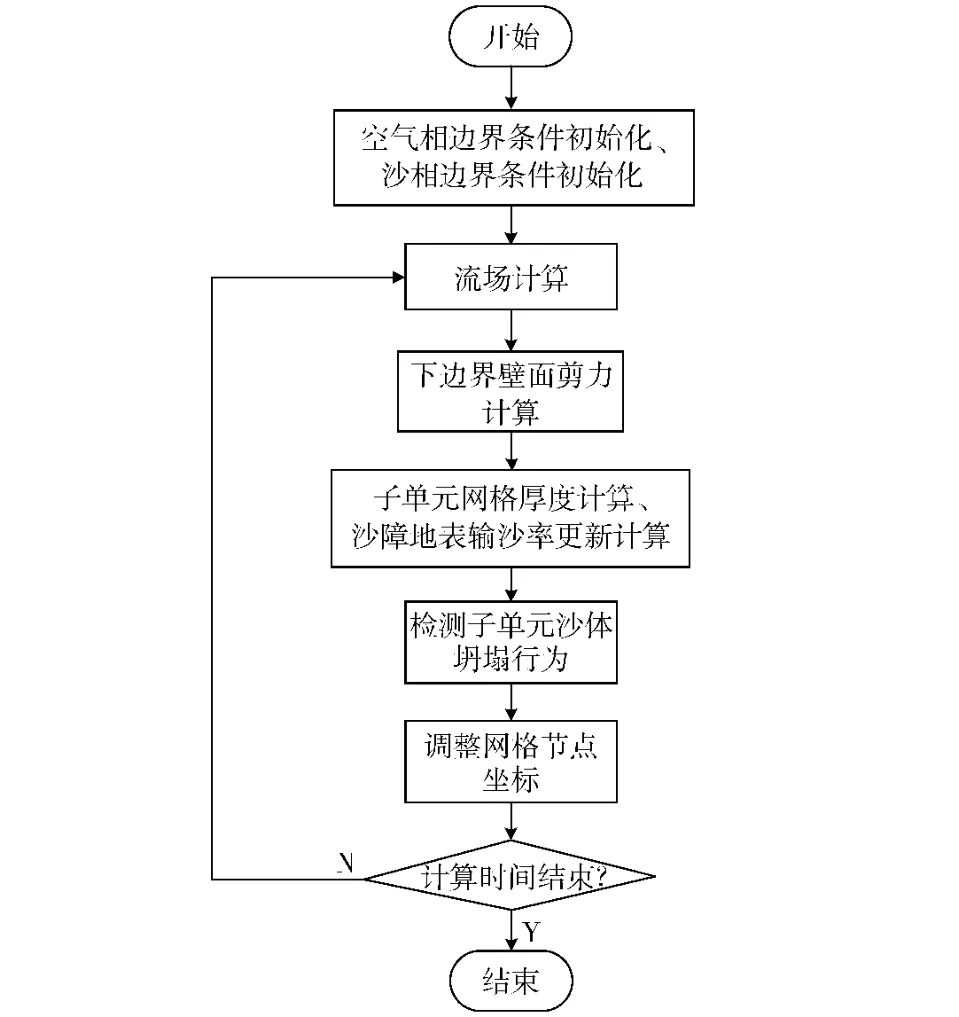
图2 程序流程图Fig．2 Flow chart of program

图3 草方格风沙作用原理图Fig．3 Schematic of interaction between wind and sand in straw checkerboard

考虑进入任意沙障方格单元内的风沙流微元的运动过程，从风沙流微元进入沙障方格范围后，与地表发生沙粒交换，风沙流率产生变化，一直到流出沙障范围这一过程。由于沙床表面的地表是否发生侵蚀还取决于此位置上方的输沙率是否达到饱和，因此需要对比地表当前位置由风蚀产生的饱和输沙率与地表上方此时的输沙率，本文应用参数c对此差值进行修正，定义为风沙流与地表相互作用产生的沙粒交换速率。c(Qerosion/n－aQin)即为地表的沙量变化速率，地表上方的风沙流与地表沙床相互作用后，沙障地表内输沙率将发生变化，Qair为变化后的沙床表面输沙率，Qair=c(Qerosion/n－aQin)+aQin。沙障内地表附近的风沙流微元会因为继续运动一部分流出沙障上空范围，与一部分的入口风沙流共同组成方格的出口输沙率，即Qout，一部分则会发生沉降，沉积在沙床表面。此模型中需要确定3个参数，入口风沙流参与地表相互作用的这部分风沙流的比例参数a，定义为风沙流进入概率;沙障方格内风沙流飞出沙障的概率b，定义为逃逸概率;沙粒交换速率c。

1.3.1 进入概率a数学模型

草方格入口风沙流进入沙障地表附近直接参与地表沙粒交换的概率，受沙障内部沙床表面高度的影响，本文假定a只与沙床表面高度有关，因此a是变量为高度h的函数。本文假定进入概率a随沙障内部平均高度变化服从指数函数分布，当沙障内部地表高度与草头高度相等时，进入沙障范围内的风沙流将全部对地表沙粒运动产生影响，此时进入概率为1。进入概率a的表达式为

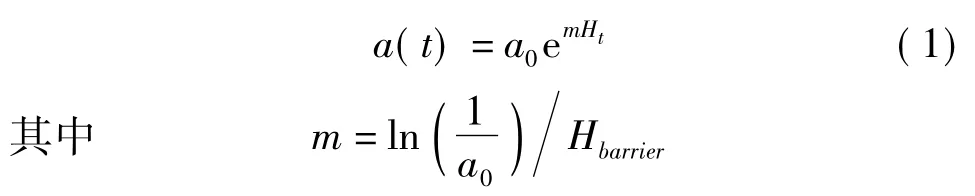
式中 t——时间，s m——高度调整系数

a(t)——t时刻的风沙流进入概率

a0——初始风沙流进入概率

Ht——t时刻沙障内部地表平均高度，m

Hbarrier——沙障草头高度，m

1.3.2 逃逸概率b数学模型

沙障内风沙流流出沙障的概率与沙障内部地表与空中沙粒交换速率、沙障内地表平均高度、沙障内风沙流速度有关，与进入概率a的数学模型相同，本文定义逃逸概率b的数学模型为指数函数模型。b的初值b0由初始化的沙障地表整体输沙率和沙粒交换速率c确定得出，c值假定仅与沙粒物理参数有关，是一个常数。初始时刻t=0时，沙障方格的出口风沙流率和入口风沙流率由沙相边界条件进行初始化。逃逸概率b的表达式为

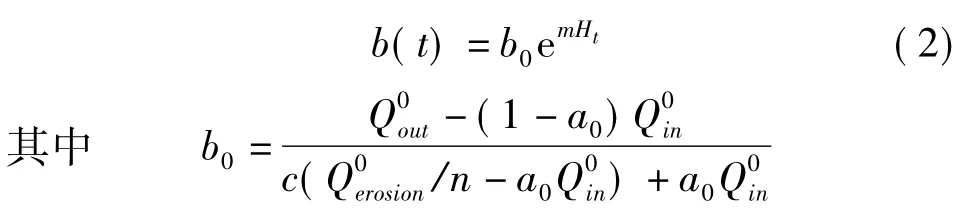
式中 b(t)——t时刻的风沙流逃逸概率

b0——t=0时的逃逸概率

n——沙障内子单元数量

1.4 草方格障间风蚀量计算

当沙床表面剪切风速超过临界起沙风速时，沙粒启动形成风沙流，并在1～2 s内逐渐保持稳定。有关剪切风速和稳定输沙率的数学模型，前人已经对其进行了大量的研究，主要分为2类，一种为O’brien-Rindlaub型方程，将地表以上一定高度的风速作为输沙率函数变量。另一种为Bagnonld型方程，将地表剪切风速作为输沙率函数变量。由于沙障地表并非平坦地面，沙障上方风速廓线不完全服从对数分布，因此，对于铺设沙障的地表，以地表剪切风速作为计算输沙率的依据是合理的。本文使用的输沙率计算公式为

式中 Qelement——子单元网格的输沙率，kg/(m·s)

Rt——沙粒启动时临界剪切风速和当前剪切风速的比值

ρs——沙粒密度，kg/m3

g——重力加速度，m/s2

u*——剪切风速，m/s

d——沙粒平均直径，mm

D——参考沙粒直径，取0.25mm

草方格内总风蚀率为

式中 i——草方格内子网格单元编号

Qelement(i)——单元i的风蚀率

1.5 子网格单元厚度计算

沙床表面的沙粒沉降分为两部分，一是由于沙床表面的风沙流和地表上沙粒相互作用产生的地表沙量变化，二是由于沙障内部风沙流在运动过程中由于沙障的阻碍和地表起伏而引起的沙粒沉降。计算网格厚度变化时，首先要计算沙障方格内部各子单元网格的沙粒变化量。

1.5.1 风沙蚀积作用产生的地表沙量变化

在气流的作用下，沙障地表会有不同程度的风沙流形成，而当前位置是否发生风蚀或者堆积取决于当前地表的摩阻风速和风沙流的供给量，即当前位置上方的风沙流浓度。沙床表面可以产生的最强风沙流与当前位置的摩阻风速有关，本文将在一定摩阻风速下产生的最大风沙流率定义为当前位置的风沙流承载力。当沙源供给量大于承载能力时，沙粒在此位置发生沉降，当沙源供给量小于承载力时，此位置发生风蚀。

沙床表面的输沙率分布取决于沙障内摩阻风速分布，显然每个单元的沙源供给量不是均匀分布，为了对模型进行简化，本文假设每个子网格单元的沙源供给量相同，如图4所示，即Qsupply=aQin。每个子单元的沙量承载力可以由式(3)计算得出，定义为 Qcapacity。

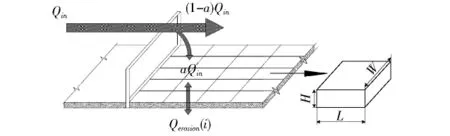
图4 沙床子单元厚度计算原理图Fig．4 Schematic of thickness calculation of sand element

图4中H为子单元厚度，L为子单元顺风向长度，W为子单元垂直风向宽度。研究表明，沙床表面从静止状态到形成饱和风沙流状态需要1～2 s的时间，故由于沙源的供给量和承载力不均衡导致的沙量变化也需要一定的时间，本模型中应用沙粒交换速率c对此结果进行修正。子单元网格沙粒变化率计算式为

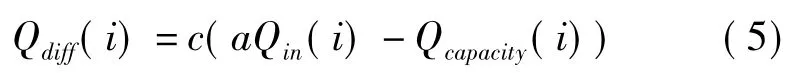
式中 Qdiff(i)——单元i的沙粒变化率，

当Qdiff(i)＞0时，风沙流中的沙粒发生沉降，当Qdiff(i)＜0时，子单元发生风蚀。

子单元高度计算式为

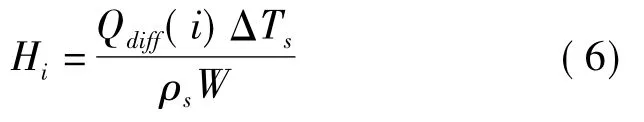
式中 Hi——单元i厚度，m

ΔTs——沙相计算时间步长，s

1.5.2 沙障阻挡及地表起伏产生的沙量沉降

风沙流在进入沙障范围后，会受到沙障的阻挡而发生明显的堆积，而地表的起伏变化同样会引起沙粒的不均匀沉降，研究表明对于沙丘地貌，风沙流在到达沙丘位置时，沙粒容易在沙丘坡脚处发生堆积，一方面由于沙丘坡脚处风速变弱，沙粒的承载能力变弱，另一方面也是由于地表起伏发生变化，沙粒从水平运动转变为沿迎风坡向上运动，需要克服重力向上爬升。本模型中将沙障内部地表风沙流的不均匀沉降表达为概率模型，通过计算沙障内部不同子网格的沉降概率，来计算子网格的沉降量。结合以往的研究，本文假定沙粒沉降概率与地表坡度变化率有关。坡度变化率越高，沙粒沉降概率越高，地表平坦时，沙粒沉降概率为0。本文模型将沙障内的地表分为3种子地形，如图5所示，可简化为坡中、坡顶和坡谷。

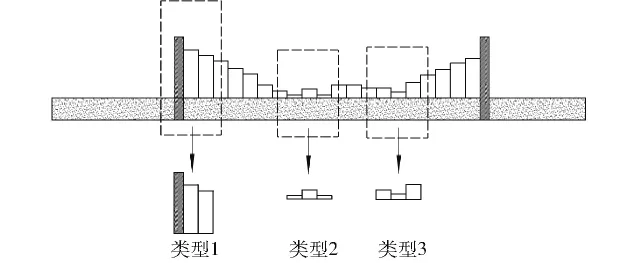
图5 沙障内地表小地形Fig．5 Sub landform in sand barrier checkerboard

沙障内子单元的坡度角变化量计算式为

式中 θdiff(i)——第i个子单元的坡度角变化量

单元i判断为坡顶地形时，θdiff(i)=0。沙障方格内子单元的概率计算式为

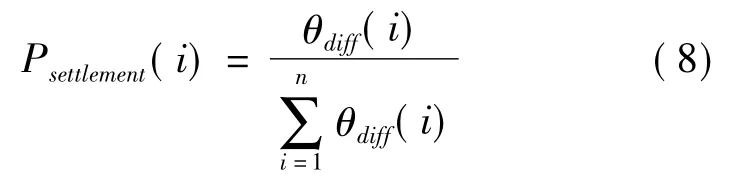
式中 Psettlement(i)——第i个子单元的沉积概率

子单元沉降量和沙障内输沙率更新示意图如图6所示。

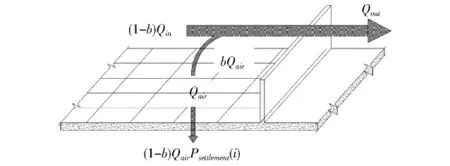
图6 沙粒沉降及沙障输沙率计算Fig．6 Calculation of sand settling and sand transport rate above sand barrier

图6中，(1－b)QairPsettlement(i)为子单元网格的沉降量，子单元厚度改变量计算与式(6)相同。沙障方格的出口输沙率更新为Qout，并作为下一个母网格的入口输沙率，计算式为

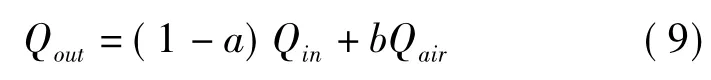
2 数值计算

本文以开源流体力学计算软件OpenFOAM为基础，编写沙相数值模型，并与流场耦合进行数值计算。

2.1 几何模型及网格划分

本文风沙两相耦合计算模型采用二维几何模型，模拟沙障在风洞环境下的积沙行为，模型计算域如图7所示。

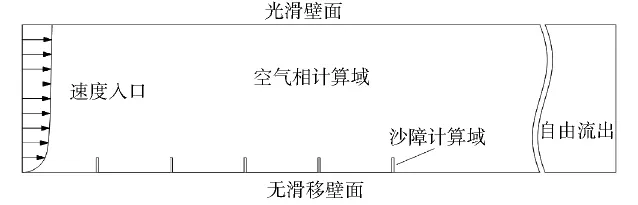
图7 沙障计算域示意图Fig．7 Schematic diagram of computational setup for sand fence

计算域由空气相计算域和沙障计算域构成，计算域高度为1 m，沙障高度为0.1 m，沙障间距为1m，入口边界到第1个沙障的距离为1 m，计算域右侧沙障到计算域出口的距离为8 m，为了后面便于动网格调整，避免出现低质量网格而增加计算误差，模型对沙障部分采用孔隙域模型，设置其孔隙为零。

流场网格尺寸为25 mm×25 mm。在使用标准k-ε湍流时，一般要求y+在30～200之间，以保证近壁面流场计算准确，壁面第 1层网格高度为1mm，壁面网格设置10层。网格划分如图8所示。

图8 计算域网格划分Fig．8 Mesh grid of computational domain

2.2 边界条件及模型参数初始化

流场左边界采用速度入口边界条件，入口风速沿高度服从对数函数分布，摩阻风速为0.6m/s。右边界采用自由流出边界，上边界采用光滑壁面边界，下边界采用无滑移壁面边界，沙障计算域设置为孔隙域模型。主要参数如表1所示。

表1 模型参数设置Tab．1 Model parameters

3 数值计算结果

对上述模型进行计算，不同时间的流场速度分布计算结果如图9所示，时间t为沙相的计算时间。时间t=0 d时，流场已经充分发展，然后开始耦合计算。从图中可以看出，t=0.5 d时，沙床表面沙障两侧最先开始积沙。随着时间的发展，沙障两侧积沙逐渐提高，沙坑表面逐渐发展为圆弧形态，由于沙坑内各位置的地表风速分布不均，圆弧最低点逐渐向下风向移动。从以往的研究和实地调查中可以看出，从定性分析上看，本模型的沙坑发展与野外观测结果较为吻合。

对野外草沙障凹坑沿主风向中线进行测量，并与数值计算结果进行对比，结果如图10所示。由图10可以看出，时间为4 d时仿真结果与本文的测量结果较为一致。时间为8 d时，仿真结果与张登山等［14］的实地测量结果接近。当仿真时间为4 d时，仿真结果与实地测量结果相比，相对误差最大的位置为凹曲面的最低点处，仿真结果比实验结果小30.80%，沙障内部凹曲面的平均绝对误差为17.86%。当仿真时间为8 d时，仿真结果与实地测量结果相比，差距最大的位置仍为凹曲面的最低点处，仿真结果比实验结果小16.94%，沙障内部凹曲面的平均绝对误差为8.52%。仿真结果小于实验结果的原因为:沙障不具有透过性时，障后涡流强度更高，沙床表面的风蚀量大于实际工况。而实际情况下，沙障存在一定的孔隙，加之草头对气流的扰动，导致沙障后涡流强度小于模拟工况，即便如此，仍可以从定量与定性上看出，模拟结果与实验结果吻合较好。

图9 流场速度分布Fig．9 Velocity distributions of wind flow field

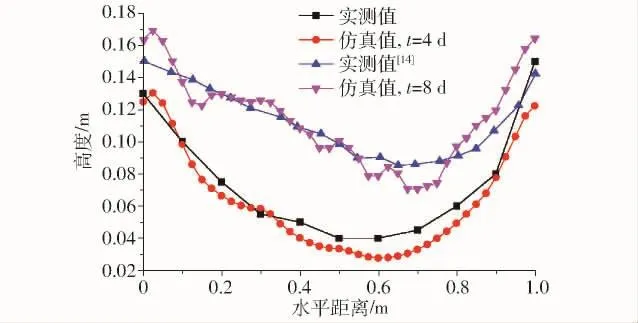
图10 仿真结果与实验结果对比Fig．10 Comparison of simulated results and field measurement results

4 讨论

沙障地表的衍化过程是沙障地表长期的风沙蚀积过程，沙障在风沙作用下，障内地表形态发生改变，而障内地表形态的改变又反过来影响流场结构的变化。虽然实际问题中，沙体颗粒数量巨大，对于沙障地表形态改变这一大空间与时间尺度的问题，现有的模型无法满足要求，但大量的沙粒运动，在风力作用下却表现出了一定的概率统计规律，如地表的风沙流结构与剪切速度的关系、沙粒长期的沉降概率等。应用概率统计模型虽然对于模拟风沙瞬时运动不够精确，但在模拟长期的风沙耦合过程方面却表现出了特有的优势，不但避免了沙粒数量带来的大计算量，而且避免了颗粒计算的小时间步长问题，使得计算速度加快。

本文的计算模型将沙障看作为非透过性薄板墙体，与实际的沙障有一定差距，导致在计算初期，地表衍化过程与实际情况有一定差距，凹坑最低点处的仿真结果比实验结果小30.80%，但随着积沙过程的持续，沙障墙体两侧被沙掩埋，墙体的孔隙作用对流场的影响减弱，使得沙障内积沙一定程度后，模拟工况和实际工况差距缩小，沙障内凹坑发展逐渐接近实际情况;另一方面，在野外环境下，沙障凹坑的发展是在多个风向下共同作用形成的，而模拟工况更接近于风洞环境，使得沙障地表的数值计算与野外地表发展过程有一定偏差。本文选择主风向明显的沙障地表进行沙障凹坑的测量，尽量缩小模拟工况和实际工况的差距，在数值计算结果与实际测量结果的对比中，数值模型计算结果虽然只代表实际工况下地表发展中经历的一个地表形态，不能精确地确定地表实际情况下发展到此形态所需要的时间，但通过数值模型，可以对比不同尺寸沙障在同一环境下地表的发展过程、衰退以及沙障可以保持固沙作用的时间，可以为沙障的尺寸设计提供参考。

5 结束语

本文提出的风沙相互作用模型基于概率统计理论，通过动网格技术调整计算域下边界，实现沙障地表的形态变化。数值计算表明，本文模型计算结果与实际沙障的地表形态发展过程较为吻合，凹坑发展过程中，初始积沙时，凹坑内积沙速度较快，而障间形成凹曲面后，地表高度增长变缓，沙障凹坑最低点向下风向移动。从沙障曲面的定量分析可以看出，沙障地表初期发展与实际环境下地表变化差距较大，相对误差最大为30.80%，平均绝对误差为17.86%。当沙障内部存在一定积沙后，数值计算与实际测量结果差距缩小，仿真结果与实验结果相比相对误差最大为16.94%，沙障内部凹曲面的平均绝对误差为8.52%，本文数值模型可以正确模拟野外沙障的凹坑发展过程。

参 考 文 献

1 庞营军，屈建军，谢胜波，等．高立式格状沙障防风效益［J］．水土保持通报，2014，34(5):11－14．PANG Yingjun，QU Jianjun，XIE Shengbo，etal．Windproof efficiency ofupright checkerboard sand-barriers［J］．Bulletion of Soil and Water Conservation，2014，34(5):11－14．(in Chinese)

2 屈建军，凌裕泉，俎瑞平，等．半隐蔽格状沙障的综合防护效益观测研究［J］．中国沙漠，2005，25(3):329－335．QU Jianjun，LING Yuquan，ZU Ruiping，et al．Study on comprehensive sand-protecting efficiency of semi-buried checkerboard sand-barriers［J］．Journal of Desert Research，2005，25(3):329－335．(in Chinese)

3 黄强，雷加强，王雪芹．塔里木沙漠公路不同地貌部位的高立式沙障阻沙特征［J］．干旱区地理，2000，23(3):227－232．HUANG Qiang，LEIJiaqiang，WANG Xueqin．Sand-obstructing effectof the high sandbarriers in the differentmorhpologic sections along the traim desert highway［J］．Arid Land Geography，2000，23(3):227－232．(in Chinese)

4 党晓宏，高永，虞毅，等．新型生物可降解PLA沙障与传统草方格沙障防风效益［J］．北京林业大学学报，2015，37(3): 118－125．DANG Xiaohong，GAO Yong，YU Yi，et al．Windproof efficiency with new biodegradable PLA sand barrier and traditional straw sand barrier［J］．Journal of Beijing Forestry University，2015，37(3):118－125．(in Chinese)

5 DONG Z B，LUOW Y，QIAN G Q，et al．A wind tunnel simulation of themean velocity fields behind upright porous fences［J］．Agricultural and ForestMeteorology，2007，146(1):82－93．

6 CORNELISW M，GABRIELSD．Optimal windbreak design for wind-erosion control［J］．Journal of Arid Environments，2005，61(2):315－332．

7 ZHANG N，KANG J，LEE S．Wind tunnel observation on the effect of a porous wind fence on shelter of saltating sand particles［J］．Geomorphology，2010，120(3):224－232．

8 DONG Z B，QIAN G Q，LUOW Y，et al．Threshold velocity for wind erosion:the effects of porous fences［J］．Environmental Geology，2006，51(3):471－475．

9 姚正毅，陈广庭，韩志文，等．机械防沙体系防沙功能的衰退过程［J］．中国沙漠，2006，26(2):226－231．YAO Zhengyi，CHEN Guangting，HAN Zhiwen，et al．Declinemechanism and process ofmechanical defense system［J］．Journal of Desert Research，2006，26(2):226－231．(in Chinese)

10 王振亭，郑晓静．草方格沙障尺寸分析的简单模型［J］．中国沙漠，2002，22(3):229－232．WANG Zhenting，ZHENG Xiaojing．A simplemodel for calculatingmeasurements of straw checkerboard barriers［J］．Journal of Desert Research，2002，22(3):229－232．(in Chinese)

11 常兆丰，仲生年，韩福桂，等．粘土沙障及麦草沙障合理间距的调查研究［J］．中国沙漠，2000，20(4):455－457．CHANG Zhaofeng，ZHONG Shengnian，HAN Fugui，et al．Research of the suitable row spacing on clay barriers and straw barriers［J］．Journal of Desert Research，2000，20(4):455－457．(in Chinese)

12 马学喜，李生宇，王海峰，等．固沙网沙障积沙凹曲面特征及其固沙效益分析［J］．干旱区研究，2016，33(4):898－904．MA Xuexi，LIShengyu，WANG Haifeng，et al．Concave surface features in sand-fixing net barriers and evaluation of sand-fixing benefits［J］．Arid Zone Research，2016，33(4):898－904．(in Chinese)

13 周丹丹，虞毅，胡生荣，等．沙袋沙障凹曲面特性研究［J］．水土保持通报，2009，29(4):22－25．ZHOU Dandan，YU Yi，HU Shengrong，et al．Concave surface characteristics of sand bag sand barrier［J］．Bulletin of Soil and Water Conservation，2009，29(4):22－25．(in Chinese)

14 张登山，吴汪洋，田慧丽，等．青海湖沙地麦草方格沙障的蚀积效应与规格选取［J］．地理科学，2014，34(5):627－634．ZHANG Dengshan，WU Wangyang，TIAN Huili，et al．effects of erosion and deposition and dimensions selection of strawcheckerboard barriers in the desert of qinghai lake［J］．Scientia Geographica Sinica，2014，34(5):627－634．(in Chinese)

15 喻黎明，邹小艳，谭弘，等．基于CFD-DEM耦合的水力旋流器水沙运动三维数值模拟［J/OL］．农业机械学报，2016，47(1):126－132．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20160117＆journal_id= jcsam．DOI:10．6041/j．issn．1000-1298．2016．01．017．YU Liming，ZOU Xiaoyan，TAN Hong，et al．3D numerical simulation of water and sediment flow in hydrocyclone based on coupled CFD-DEM［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2016，47(1):126－132．(in Chinese)

16 喻黎明，谭弘，邹小艳，等．基于CFD-DEM耦合的迷宫流道水沙运动数值模拟［J/OL］．农业机械学报，2016，47(8): 65－71．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20160810＆journal_id=jcsam．DOI: 10．6041/j．issn．1000-1298．2016．08．010．YU Liming，TAN Hong，ZOU Xiaoyan，et al．Numerical simulation of water and sediment flow in labyrinth channel based on coupled CFD-DEM［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2016，47(8):65－71．(in Chinese)

17 CHEN G H，WANG W W，SUN C F，et al．3D numerical simulation of wind flow behind a new porous fence［J］．Powder Technology，2012，230:118－126．

18 LOPESA M G，OLIVEIRA L A，ALMERINDO D，et al．Numerical simulation of sand dune erosion［J］．Environmental Fluid Mechanics，2013，13(2):145－168．

19 TONG D，HUANG N．Numerical simulation of saltating particles in atmospheric boundary layer over flat bed and sand ripples［J］．Journal of Geophysical Research:Atmospheres，2012，117(D16):16205．

20 HUANG N，XIA X P，TONG D．Numerical simulation ofwind sand movement in straw checkerboard barriers［J］．The European Physical Journal，2013，36:1－7．

21 SCHMEECKLEM W．Numerical simulation of turbulence and sediment transport of medium sand［J］．Journal of Geophysical Research Earth Surface，2014，119(6):1240－1262．

22 DURAN O，CLAUDIN P，ANDREOTTIB．Direct numerical simulations of aeolian sand ripples［J］．Proceedings of the National Academy of Sciences，2014，111(44):15665－15668．

Numerical Method of Surface Morphology Evolution of Sand Barrier

SUN Hao LIU Jinhao HUANG Qingqing
(School of Technology，Beijing Forestry University，Beijing 100083，China)

A new numerical model of sand-wind interaction was proposed to predict the surface morphology evolution and provide the basis for dimension design of sand barrier．Based on the theory of probability and statistics，the model realized sand-wind interaction process by calculating wind erosion and deposition probability of sand grains at different wind speeds．Firstly，the model parameters of air phase and sand phase were initialized，and the velocity distribution can be calculated by computational fluid dynamic(CFD)method．Secondly，the wind friction velocity of sand element was calculated by using velocity field data，and the sand transport rate can be obtained．Finally，the thickness of sand elementwas calculated by calculating sand change in one time step．The moving mesh technique was used to change the fluctuation of the sand bed by changing the coordinates of lower boundary nodes．The numerical resultswere compared with the measured results，which showed that the numerical results of the surfacemorphology in the sand barrierwere close to themeasured results．The lowest point of pitwas themaximum position thatmoved along the downwind area，the average absolute errorwas17.86%when t=4 d，the error was decreased gradually with the increase of sand accumulation，the average absolute error was8.52%when t=8 d．Both qualitative and quantitative resultswere consistentwith themeasured results，and themodel can simulate the surfacemorphology evolution of sand barrier correctly．

sand barrier;surface process;dynamic mesh;numericalmethod

S727.23;S775

A

1000-1298(2017)07-0265-07

2017-03-25

2017-05-03

“十二五”国家科技支撑计划项目(2015BAD07B00)

孙浩(1989—)，男，博士生，主要从事环境流体力学和风沙物理学研究，E-mail:251045257@qq．com

刘晋浩(1958—)，男，教授，博士生导师，主要从事林业装备自动化及智能化研究，E-mail:liujinhao@vip．163．com

10．6041/j．issn．1000-1298．2017．07．033