基于SFLA-M-L模型的景观格局优化研究
2017-07-31张启斌岳德鹏方敏哲
张启斌 岳德鹏 方敏哲 张 耘 李 倩 马 欢
(1.北京林业大学精准林业北京市重点实验室,北京100083;2.北京联合大学应用科技学院,北京102200; 3.北京林业大学林学院,北京100083)
基于SFLA-M-L模型的景观格局优化研究
张启斌1岳德鹏1方敏哲1张 耘2李 倩3马 欢1
(1.北京林业大学精准林业北京市重点实验室,北京100083;2.北京联合大学应用科技学院,北京102200; 3.北京林业大学林学院,北京100083)
以内蒙古自治区巴彦淖尔市磴口县为研究区,基于混合蛙跳算法,耦合逻辑回归与马尔可夫模型构建了SFLA-M-L(Shuffled frog leaping algorithm-Markov-logistic regression)模型。利用逻辑回归,综合考虑高程、坡度、地下水埋深、干旱度指数、归一化植被指数与当前景观分布进行了景观适宜性分析;利用Markov模型,构造了县域景观转移概率矩阵。利用景观适宜性指数和景观聚集度指数构造目标函数,以景观转移概率矩阵为景观变异的控制条件,对2016年景观格局分布进行了县域景观格局优化。优化结果中,景观聚集度为96.71%,比2016年景观分布提升了6.43个百分点;景观适宜性指数为96.23%,比2016年景观分布提升了4.18个百分点;不同景观类型间相互转移超出转移概率矩阵控制仅4.66 km2,确保了优化结果的合理性。
景观格局优化;混合蛙跳算法;逻辑回归模型;马尔可夫模型
引言
景观格局指的是不同属性、形状、大小的景观斑块在空间上的镶嵌形式,它决定着资源和环境在空间的分布形式,对多种生态过程产生重要影响[1-3]。景观格局优化是指在充分理解格局和过程间耦合关系的基础上,通过调整优化各景观类型斑块的空间分布和数量,使其达到最大的生态效益[4-5]。概念模型、数学模型、GIS技术等是景观格局优化的常用方法,然而景观格局优化涉及到的栅格空间数据具有像元数量多、计算量大的特点,上述方法已经难以满足景观格局优化对于高性能计算的要求。针对这一问题,众多学者将智能优化算法与GIS空间处理技术相结合,构建智能景观格局优化模型[6-8]。
混合蛙跳算法已经在众多领域的优化问题中得到应用,如路径规划问题、复杂产品装配序列问题、Web用户聚类问题等。在景观格局优化领域,郭小燕等[9-12]将混合蛙跳算法用于土地利用优化问题,以生态系统服务功能值和土地利用格局紧凑度为目标函数对兰州市的土地利用格局进行了优化,取得了较好的研究结果。然而单独的混合蛙跳算法在进行景观格局优化时,不能充分考虑研究区的具体生态环境特点,传统景观格局优化方法中的地形、水文、生态等因子均未在优化过程中体现。因此在混合蛙跳算法的基础上耦合其他模型,充分考虑多种因子进行景观格局优化具有实际意义。
本文以内蒙古自治区巴彦淖尔市磴口县为例,基于混合蛙跳算法耦合逻辑回归与马尔可夫模型构建SFLA-M-L(Shuffled frog leaping algorithm-Markovlogistic regression)模型,实现对景观格局优化模型的改进。利用该模型综合考虑多种因子,并对不同景观类型间的互相转移进行上限控制,使景观格局优化结果更贴近研究区实际情况。
1 SFLA-M-L模型构建
混合蛙跳算法是群智能优化算法的一种,该算法集成了遗传算法和群智能算法的优点,实现了全局和局部搜索能力的均衡,算法简单,易于实现[13]。本文基于混合蛙跳算法,耦合逻辑回归模型与Markov模型构建SFLA-M-L模型,用于研究区景观格局优化。
1.1 模型关键技术
1.1.1 定义解空间与青蛙个体
以景观格局栅格数据为数据源进行景观格局优化,设栅格数据有m行n列,则模型的目标搜索空间为m×n维的矩阵。算法首先在目标搜索空间内产生F只青蛙(即F种解)生成初始种群,景观格局栅格数据中的像元依次排列,构成青蛙的基因,第i只青蛙表示问题的第i个解,其数学表示为

式中 Xi——编号为i的青蛙
j——青蛙所在位置横坐标
k——青蛙所在位置纵坐标
xi,j,k——青蛙Xi在位置(j,k)的基因
青蛙基因的取值为1~6的整数,从小到大分别代表了林地、耕地、沙地、山地、水体、建筑用地。
1.1.2 适应度函数建立
适应度函数确定了种群中每只青蛙的优劣,控制着种群的进化方向[14]。景观破碎化阻碍物种间的物质交流,减小物种生存空间,改变生态系统特性,影响系统内的能量平衡和物质流动,加剧物种入侵等,因此本文在适应度函数中考虑了景观聚集度[15-16]。同时,研究利用的逻辑回归模型考虑了高程、地下水埋深、归一化植被指数等因子,分析了景观格局在空间分布上的适宜性,确保土地利用优化结果的现实意义[17]。本文利用聚集度指数与土地利用适宜性共同判定每只青蛙的适应度,适应度函数的具体形式为
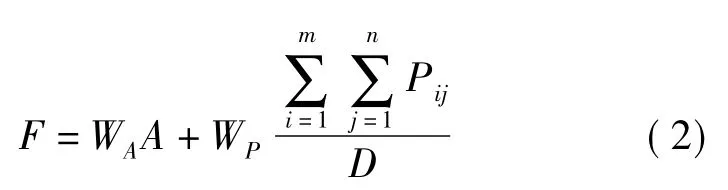
式中 F——适应度
WA——聚集度指数指标权重
WP——景观适宜性指数指标权重
A——某只青蛙所代表的景观格局优化方案的景观聚集度指数
Pij——某只青蛙在(i,j)处的基因所对应的景观格局适宜性指数
D——景观格局栅格数据中的像元个数
Pij通过逻辑回归计算得到,回归中的自变量为多种因子(高程、地下水埋深、归一化植被指数等),回归的结果为对应每个景观类型的适宜性图,通过确定该青蛙在像元(i,j)的景观类型并对照适宜性图集确定该位置景观格局适宜性指数。
1.1.3 子群体划分方法
利用1.1.2节中的适应度函数判定初始种群中每只青蛙的适应度,将青蛙个体按照适应度从优到劣排序,将整个青蛙种群划分为M个子群体,将适应度排名与青蛙的子群体数相除,按照相除所得的余数划分子群体范围:将余数为1的青蛙分入第1子群体,余数为2的青蛙分入第2子群体,依次类推,将余数为M-1的青蛙分入第M-1子群体,将余数为0的青蛙分入第M子群体,最终将所有青蛙个体划分完毕。以子群体为单位进行局部深度搜索,即在子群体的每次迭代中,首先确定群组内的最优青蛙Xb,最差青蛙Xw,全局最优青蛙Xg,通过对当前子群体中最差个体进行更新与变异操作实现对整个群体的优化。
1.1.4 更新与变异操作
(1)更新操作
在以子群体为单位进行局部搜索时,子群体内的最差青蛙Xw向群体内或子群体内最优青蛙Xb学习,学习时采用随机替换算子,系统首先产生随机数e、c、h、f,其中e、h∈(1,m),c、f∈(1,n),在景观格局栅格数据中定位坐标为(e,h)和(c,f)的像元,以该两像元分别作为左上角与右下角生成矩形范围,截取学习目标青蛙Xb在该范围内的基因信息,并用其替换当前子群体内最差青蛙Xw对应范围的基因,完成更新操作,如图1所示。
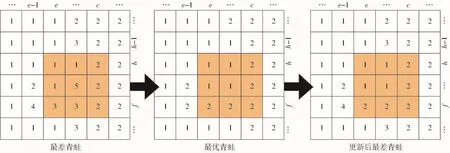
图1 更新操作Fig.1 Diagram of update operation
(2)变异操作
根据适应度函数进行判定,当子群体内的最差青蛙Xw经过更新操作并没有得到更好的适应度时,对其进行变异操作,变异操作流程如图2所示。
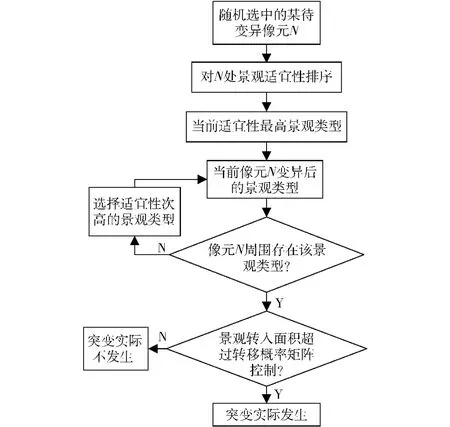
图2 变异操作Fig.2 Diagram ofmutation operation
变异时,在栅格空间内随机选取k个像元,综合考虑逻辑回归与景观聚集度2方面,对选中的像元进行变异,变异策略如下:根据适宜性图集,对变异像元位置上的景观类型适宜性进行排序,找到适宜度最高的景观种类;搜索变异像元相邻的8个像元,确认相邻像元中是否存在与适宜度最高的景观种类相同的景观类型:若是,则突变为该类型完成变异操作;若否,则选择适宜性次高的景观类型再次搜索,直到变异操作完成。判断该变异发生后,景观转移的面积是否超过景观格局转移概率矩阵的控制,若没有超过,则该变异实际上发生,否则,该变异实际上不发生。
1.2 模型优化步骤
本研究构建的景观格局优化模型用不同的青蛙代表每种景观格局优化方案,以C#为编程语言,在.net平台下调用arc Objects二次开发组件实现运行,通过高速迭代搜索最优的景观格局优化方案,其优化步骤描述如下:
(1)生成初始青蛙种群,确定算法参数
为避免随机生成青蛙导致的盲目搜索,本研究以研究区2016年的景观格局栅格数据为基础,对其进行1.1.4节中的变异操作,生成初始种群,并按照1.1.3节所述方法划分青蛙子群体。本研究种群中共产生1 000只青蛙,生成子群体10个,每个子群体内有100只青蛙,算法迭代次数设置为1 000次,聚集度指数A与土地利用适宜度P的权重均设置为0.5。
(2)划分子群体及子群体内局部搜索
按照1.1.3节中所述方法划分子群体,组内最差青蛙Xw通过1.1.4节中的更新与变异操作向组内最优青蛙或全局最优青蛙Xb学习,子群体内一次完整的搜索过程如图3所示,一次搜索完成后,对子群体内的青蛙进行重新排序,确定新的组内最优青蛙和最差青蛙,开始下一次搜索,直到达到局部搜索次数停止搜索。

图3 子群体内部搜索Fig.3 Diagram of sub-group search
(3)全局搜索
当每个子群体均完成局部搜索后,将每个子群体内的青蛙合并重新进行1.1.3节中所述的子群体划分过程,使得子群体内的基因信息得到全局交换,之后再进行局部搜索。当全局优化完成规定的迭代次数后,输出此时的全局最优解作为最终的景观格局优化结果。
(4)限制条件
为防止沙漠化进程、减少水土流失,并充分考虑数据可得性,根据《水土保持工作条例》等政策法规,设置约束条件如下:坡度大于25°的像元禁止向耕地变异;坡度大于15°的像元禁止向建设用地变异;坡度大于30°的像元禁止向林地变异;禁止其他景观类型与山地间产生变异。
(5)优化结果输出
蛙群满足迭代终止条件后,将全局最优青蛙输出为栅格专题图,作为最终的景观格局优化方案。
图4为模型的整体流程。

图4 模型优化步骤Fig.4 Model optimization procedure
2 模型案例研究
图5 研究区位置Fig.5 Location of study area
2.1 研究区概况
磴口县位于内蒙古自治区巴彦淖尔市,地处106°10'~107°10'E、40°10'~40°57'N,位于内蒙古自治区西南部,如图5所示。磴口县县域西侧为狼山山脉,东侧为黄河,北侧为河套平原,南侧部分为乌兰布和沙漠。县域内部从东南向西北逐渐由绿洲向沙漠过渡,属典型的荒漠绿洲交错区,生态区位极为关键[18]。县域大陆性气候特征显著,降水稀少(144.5mm),蒸发强烈(2 397.6 mm),年均风速3m/s,风蚀强烈,土地沙化风险较高。近年来磴口县景观格局发生了较大变化,景观破碎化、景观空间分布的不合理是该区域当前面临的突出问题之一[19-20]。
2.2 数据来源与处理
本研究涉及的景观格局数据来自磴口县2007年与 2016年遥感影像,2007年遥感影像采自Landsat5 TM传感器(共7个波段,分辨率30 m× 30m),2016年遥感影像采自Landsat 8 OLI传感器(共9个波段,Band 8分辨率为15m×15m,其他波段分辨率为30 m×30 m),影像采集时间均为8、9月份。所有影像均为tif格式,由地理空间数据云下载,网址为http:∥www.gscloud.cn/。本研究景观格局分类体系根据《生态环境状况评价技术规范》与县域具体特点建立,景观类型分为林地、耕地、沙地、水体、山地、建筑用地6种。影像分类与预处理借助ENVI 5.2软件完成。
高程与坡度数据同样来自地理空间数据云(http:∥www.gscloud.cn/),下载后经裁剪拼接制成。地下水埋深数据通过磴口县境内103个常年观测井的实测数据经空间差值得到。干旱度指数由中国林科院沙林中心所测的多年平均蒸发量和多年平均降水量作比制成,归一化植被指数由遥感影像反演得到。
2.3 景观适宜性分析
利用逻辑回归模型,考虑高程、坡度、地下水埋深、干旱度指数、归一化植被指数与当前景观分布,对县域每种景观类型的空间分布适宜性进行分析。模型通过IDRISISelva软件运行,每种景观类型的景观适宜性指数如图6所示。
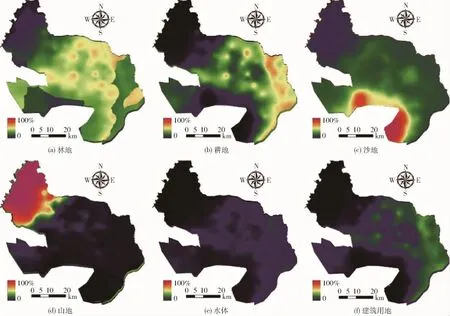
图6 景观适宜性指数Fig.6 Landscape suitability results
由图6可知,磴口县多种景观类型中,山地景观的高适宜性空间十分集中,当前山体的空间分布范围内,景观适宜性指数达到100%,在当前山体景观的外围迅速衰减到0。沙地在县域南部的适宜性指数较高,部分地区达到100%,而县域中部仅有少数地区达到了50%。林地景观在当前耕地与沙地的交错地带有较高的适宜性,然而其适宜性在县域东部黄河流经区域出现了较为明显的断裂,适宜性突然降低,这主要是由于该地区地势平坦,地下水埋深较浅且灌溉水源充足,更加适宜耕地景观的分布。耕地景观在黄河沿岸土地的适宜性较高,适宜性指数最高处达到64%,在县域中部水源较为丰富地区也有较高的分布适宜性。建筑用地的适宜性分布与耕地较为一致,但是其适宜性指数普遍较低,最高处为35%。水体的景观适宜性指数为研究区最低,在黄河流经地区为28%,这与水体面积较小有关。
2.4 景观转移概率分析
利用Markov模型,对研究区未来的景观面积变化进行预测。本文选取2007年与2016年2个时间节点的景观格局分布数据,利用IDRISISelva软件的Markov模块构建Markov模型,生成2016—2025年各景观类型间的转移概率矩阵,对县域未来景观格局的数量转移进行预测,并以此作为蛙跳算法变异操作中的控制条件,确保景观格局优化结果与实际情况吻合,结果如表1所示。

表1 景观格局转移控制面积Tab.1 Landscape transfer control area km2
由表1可知,在县域未来的演化趋势中,林地是转化最为活跃的景观类型,其向耕地和沙地的可能转移面积分别达到了124.19 km2和272.26 km2,其他5种景观种类向该地类的可能转移面积达到了543.72 km2。建筑用地与其他景观间的可能转移面积同样较大,且转出量明显大于转入量,该景观类型向林地与耕地的转移量达到了189.12 km2,占2016年建筑用地景观总面积的65.12%。沙地与其他景观类型间的可能转移面积较小,而与林地间的可能转移面积较大,其中沙地转向林地为231.96 km2,林地转向沙地为272.26 km2。磴口县水体景观面积较小,与林地和沙地间的可能转移面积较大,与其他景观间的转移较小。山地景观的可能转移面积为所有景观类型中最小,可能的转出与转入面积仅有6.36 km2与10.41 km2。
2.5 基于SFLA-M-L模型的景观格局优化
本研究以磴口县2016年的景观格局分布图为基础数据(图7a),按照1.2节中描述的算法,在.net平台下调用arc Objects组件,利用C#编写程序,对研究区的景观格局进行了优化,优化结果如图7b所示。为了验证逻辑回归模型及马尔可夫模型与混合蛙跳算法耦合的效果,本研究模型中去除上述2种模型,仅以景观聚集度为目标函数基于混合蛙跳算法构建 SFLA-AI(Shuffled frog leaping algorithmaggregation index)模型进行研究区的景观格局优化,结果如图7c所示。

图7 模型优化结果对比Fig.7 Optimization results comparison
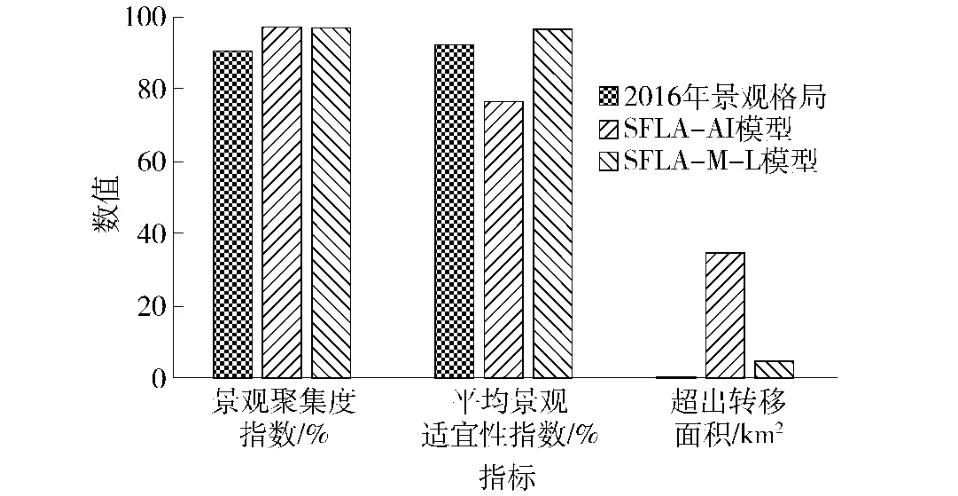
图8 景观格局优化结果各指标对比Fig.8 Indices comparison of landscape pattern optimization results
通过对优化结果的目视观察可知,2种优化模型的景观聚集度得到了较明显的提高,各景观类型的破碎化得到了很好的控制。对研究区2016年景观格局分布及2种优化结果的景观聚集度指数、平均景观适宜性指数、超出转移概率矩阵控制的转移面积进行计算,结果如图8所示。由图8可知,SFLA-M-L模型优化结果的景观聚集度指数为96.71%,SFLA-AI模型的景观聚集度指数为96.95%,2种优化结果不存在明显区别,相比优化前的90.28%都有明显提高。对2种模型优化结果的景观平均适宜性进行分析可知,SFLA-AI模型与SFLA-M-L模型的平均景观适宜性指数分别为76.33%与 96.23%,而优化前景观的适宜性为92.05%,SFLA-M-L模型明显更高。更高的景观适宜性指数能确保对县域土地的因地制宜,避免在水土条件欠佳的地方进行植树造林、开垦耕地等活动,对县域土地的合理利用具有重要作用。对2种优化结果中超出转移概率矩阵的转移面积进行计算可知,SFLA-M-L模型几乎没有超出控制(超出面积为4.66 km2),而SFLA-AI模型的模拟结果中超出了34.52 km2,其中建筑用地向林地的转移超出转移概率矩阵13.59 km2,与转移概率矩阵控制面积相差较大。优化结果中某几种景观类型间过大的转移面积将导致优化结果与县域实际情况相差过远,使景观格局优化方案的实施面临困难,因此在优化算法中加入景观格局转移概率矩阵的控制十分必要。
3 结论
(1)以混合蛙跳算法为基础,耦合Markov模型与逻辑回归模型构建了SFLA-M-L模型用于景观格局优化,该模型以景观聚集度指数、景观适宜性指数为目标函数,综合考虑了高程、坡度、地下水埋深、干旱度指数、归一化植被指数与当前景观分布多个因子。在变异操作中通过Markov模型生成的景观转移概率矩阵作为景观转移面积的控制,使优化结果更符合实际。
(2)选取典型荒漠绿洲交错区内蒙古自治区巴彦淖尔市磴口县为研究区,利用SFLA-M-L模型对研究区景观格局进行了优化。为研究SFLA-M-L模型的优化效果,在模型中去除逻辑回归模型与Markov模型,仅以景观聚集度为约束条件构建SFLA-AI模型,再次进行了景观格局优化。对2种模型的模拟结果进行对比可知,2种模型均使得县域景观格局的聚集度得到提高,而SFLA-M-L模型的优化结果有更高的景观适宜性指数(96.23%),且景观转移面积几乎未超过景观转移概率矩阵的控制,仅超出4.66 km2。
1 TURNER M G.Landscape ecology:the effect of pattern on process[J].Annual Review of Ecology&Systematics,2003,20(20):171-197.
2 岳德鹏,于强,张启斌,等.区域生态安全格局优化研究进展[J/OL].农业机械学报,2017,48(2):1-10.http:∥www.jcsam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170201&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2017.02.001.YUE Depeng,YU Qiang,ZHANG Qibin,et al.Progress in research on regional ecological security pattern optimization[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2017,48(2):1-10.(in Chinese)
3 岳德鹏,王计平,刘永兵,等.GIS与RS技术支持下的北京西北地区景观格局优化[J].地理学报,2007,19(11):1223-1231.YUE Depeng,WANG Jiping,LIU Yongbing,et al.Landscape pattern optimization based on RS and GIS in northwest of Beijing[J].Acta Ecographica Sinica,2007,19(11):1223-1231.(in Chinese)
4 韩文权,常禹,胡远满,等.景观格局优化研究进展[J].生态学杂志,2005,24(12):1487-1492.HANWenquan,CHANG Yu,HU Yuanman,et al.Research advance in landscape pattern optimization[J].Chinese Journal of Ecology,2005,24(12):1487-1492.(in Chinese)
5 刘杰,叶晶,杨婉,等.基于GIS的滇池流域景观格局优化[J].自然资源学报,2012,27(5):801-808.LIU Jie,YE Jing,YANG Wan,et al.A GIS-based landscape pattern optimization approach for lake Dianchi Watershed[J].Journal of Natural Resources,2012,27(5):801-808.(in Chinese)
6 欧定华,夏建国.基于粒子群算法的大城市近郊区景观格局优化研究——以成都市龙泉驿区为例[J].地理研究,2017,36(3):553-572.OU Dinghua,XIA Jianguo.Landscape pattern optimization in peri-urban areas based on the particle swarm optimization method:a case study in Longquanyi District of Chengdu[J].Geographical Research,2017,36(3):553-572.(in Chinese)
7 赵冬玲,杜萌,杨建宇,等.基于CA-Markov模型的土地利用演化模拟预测研究[J/OL].农业机械学报,2016,47(3): 278-285.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160339&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.03.039.ZHAO Dongling,DU Meng,YANG Jianyu,et al.Simulation and forecast study of land use change based on CA-Markov model[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(3):278-285.(in Chinese)
8 杨励雅,邵春福,聂伟.基于混合遗传算法的城市土地利用形态与交通结构的组合优化[J].上海交通大学学报,2008,42(6):896-899.YANG Liya,SHAO Chunfu,NIE Wei.Hybrid genetic algorithm for integrated optimization of urban land use pattern and transportation structure[J].Journal of Shanghai Jiaotong University,2008,42(6):896-899.(in Chinese)
9 郭小燕,刘学录,王联国.基于混合蛙跳算法的土地利用格局优化[J].农业工程学报,2015,31(24):281-288.GUO Xiaoyan,LIU Xuelu,WANG Lianguo.Land use pattern optimization based on shuffled frog leaping algorithm[J].Transactions of the CSAE,2015,31(24):281-288.(in Chinese)
10 EBRAHIMI J,HOSSEINIAN S H,GHAREHPTTIAN G B.Unit commitment problem solution using shuffled frog leaping algorithm[J].IEEE Transactions on Power Systems,2011,26(2):573-581.
11 LUO Jiaping,LIXia,CHEN Minrong,etal.A novel hybrid shuffled frog leaping algorithm for vehicle routing problem with time windows[J].Information Sciences,2015,316:266-292.
12 ARSHISS,ZOLFAGHARIA,MIRVAKILISM.A multi-objective shuffled frog leaping algorithm for in-core fuelmanagementoptimization[J].Computer Physics Communications,2014,185(10):2622-2628.
13 崔文华,刘晓冰,王伟,等.混合蛙跳算法研究综述[J].控制与决策,2012,27(4):481-486.CUIWenhua,LIU Xiaobing,WANGWei,et al.Survey on shuffled frog leaping algorithm[J].Control and Decision,2012,27(4):481-486.(in Chinese)
14 金芬,孙春华,钟鸣.遗传算法中适应度函数的改进[J].机械设计与制造,2010(3):218-219.JIN Fen,SUN Chunhua,ZHONG Ming.Improvement of fitness function in genetic algorithm[J].Machinery Design&Manufacture,2010(3):218-219.(in Chinese)
15 刘建锋,肖文发,江泽平,等.景观破碎化对生物多样性的影响[J].林业科学研究,2005,18(2):222-226.LIU Jianfeng,XIAOWenfa,JIANG Zeping,et al.A study on the influence of landscape fragmentation on biodiversity[J].Forest Research,2005,18(2):222-226.(in Chinese)
16 覃凤飞,安树青,卓元午,等.景观破碎化对植物种群的影响[J].生态学杂志,2003,22(3):43-48.TAN Fengfei,AN Shuqing,ZHUO Yuanwu,etal.Effectof landscape fragmentation on plant populations[J].Chinese Journalof Ecology,2003,22(3):43-48.(in Chinese)
17 谭龙,陈冠,王思源,等.逻辑回归与支持向量机模型在滑坡敏感性评价中的应用[J].工程地质学报,2014,22(1):56-63.TAN Long,CHEN Guan,WANG Siyuan,et al.Landslide susceptibilitymapping based on logistic regression and support vector machine[J].Journal of Engineering Geology,2014,22(1):56-63.(in Chinese)
18 于强,岳德鹏,张启斌,等.磴口县荒漠绿洲景观时空演变及其格局特征分析[J].生态科学,2016,35(6):73-83.YU Qiang,YUE Depeng,ZHANG Qibin,et al.Spatial-temporal evolution and pattern characteristics of desert oasis landscape in Dengkou County[J].Ecological Science,2016,35(6):73-83.(in Chinese)
19 张启斌,岳德鹏,于强,等.林业生态工程建设对磴口县景观格局演变及重心迁移的影响[J].浙江农业学报,2017,29(2):261-269.ZHANG Qibin,YUEDepeng,YU Qiang,et al.Effects of forestry ecological projects on landscape pattern evolution and migration of barycenter in Dengkou County[J].Acta Agriculturae Zhejiaugeusis,2017,29(2):261-269.(in Chinese)
20 于强,岳德鹏,DIYang,等.基于EnKF-MCRP模型的生态用地扩张模拟研究[J/OL].农业机械学报,2016,47(9):285-293.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160939&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.09.039.YU Qiang,YUE Depeng,DIYang,et al.Simulation on ecological land use expansion based on EnKF-MCRPmodel[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(9):285-293.(in Chinese)
Landscape Pattern Optim ization Based on SFLA-M-L Model
ZHANG Qibin1YUE Depeng1FANG Minzhe1ZHANG Yun2LIQian3MA Huan1
(1.Beijing Key Laboratory of Precision Forestry,Beijing Forestry University,Beijing 100083,China 2.College of Applied Science and Technology,Beijing Union University,Beijing 102200,China 3.College of Forestry,Beijing Forestry University,Beijing 100083,China)
Landscape pattern determines the local distribution of resources and habitats,which has an important impact on a variety of ecological processes.Based on the full understand of the coupling relationship between landscape pattern and ecological processes,landscape pattern optimization is aimed at achieving the maximum ecological benefits through the adjustment of the landscape patches’spatial distribution and size.In order to considermore factors in landscape pattern optimization and make the optimization resultsmore scientific and reasonable,an SFLA-M-Lmodelwas built based on shuffled frog leaping algorithm(SFLA),logistic regression model and Markov model.The landscape pattern of Dengkou County,Bayannaoer City,Inner Mongoliawas optimized to verify themodel.Logistic regression model was used to analyze the landscape pattern suitability based on DEM,slope,under ground water depth,aridity index,NDVI and current landscape distribution.Markov model was used to build the landscape transition probability matrix.The objective function of SFLA-M-L was built based on the landscape suitability atlas and landscape aggregation index.Landscape pattern transition probability matrix was used to restrict the transfer of different landscape types.In the optimization results,the landscape aggregation index was 96.71%,which was 6.43 percentage points higher than the landscape pattern in 2016;landscape suitability index was96.23%,which was4.18 percentage points higher than the landscape pattern in 2016;the transfer area beyond the control of landscape pattern transition probabilitymatrix was only 4.66 km2,and the rationality of the optimization resultswas ensured.
landscape pattern optimization;shuffled frog leaping algorithm;logistic regression model; Markovmodel
X171.1;S181
A
1000-1298(2017)07-0159-08
2017-04-25
2017-05-20
国家自然科学基金项目(41371189)和“十二五”国家科技支撑计划项目(2012BAD16B00)
张启斌(1990—),男,博士生,主要从事3S技术在生态环境中的应用研究,E-mail:bin0538@outlook.com
岳德鹏(1963—),男,教授,博士生导师,主要从事景观生态学和土地评价研究,E-mail:yuedepeng@126.com
10.6041/j.issn.1000-1298.2017.07.020
