基于最优特征加权的图像分类算法

王玉晶

(阿坝师范学院教务处， 四川 汶川 623002)

基于最优特征加权的图像分类算法

王玉晶

(阿坝师范学院教务处， 四川 汶川 623002)

通过研究图像分类过程中特征选择和分类器构建问题， 提出了一种基于最优特征加权的图像分类算法. 首先提取图像的颜色和纹理特征， 接着采用混沌粒子群优化算法对特征的权值进行求解， 确定每一个特征对图像分类的贡献， 最后采用相关向量机对加权的图像样本集进行学习， 构建分类器， 从而实现图像的分类. 实验结果表明， 相对于当前较流行的图像分类模型， 该模型不仅能够提高图像的分类准确率， 而且能够大幅度减少了图像的分类时间， 具有一定的实际应用价值.

图像分类； 特征选择； 混沌粒子群算法； 相关向量机

0 引 言

随着图像处理技术的不断成熟， 网络上图像数量急剧增加， 对大规模图像进行有效管理， 快速、 准确找到用户需要的图像具有十分重要的意义[1]. 图像分类是图像管理中的关键技术， 因此， 如何构建性能优异的图像分类模型， 提高图像的检索效率和正确率显得尤为重要[2].

为了提高图像分类的正确率， 提出一种混沌粒子群(Particles Swarm Optimization， PSO)算法优化特征权值的图像分类模型(PSO-RVM)， 该模型采用混沌粒子群算法确定特征权值， 并采用相关向量机(Relevance Vector Machine, RVM)构建图像分类器. 仿真实验结果表明， PSO-RVM不仅提高了图像分类的正确率， 而且图像分类速度得到大幅提升， 具有较高的实际应用价值.

1 相关研究工作

图像分类属计算模式识别中的多分类问题， 因此， 特征提取和选择、 分类器设计是两个最为关键的过程[3]. 当前图像分类特征主要有颜色、 纹理、 形状等， 由于单一特征只能描述图像一方面的信息， 当图像受到外界影响时， 就难以准确描述图像类别信息[4]. 而不同特征可以从多方面描述图像类别信息， 实现优势互补， 因此当前学者们主要提取多种特征进行图像分类[5]. 然而多特征数量比较大， 使图像分类器的输入向量维数过高， 在图像分类器学习过程中， 易出现“维数灾”等难题， 而且特征之间存在一些冗余信息， 对图像分类结果产生不利影响， 为此， 将特征输入到分类器学习之前， 需求对特征进行优化和选择[6]. 当前传统特征选择算法主要有： 主成分分析、 线性判别分析等， 这些算法具有速度快、 效率高等优点， 但得到的结果可解释性差， 破坏了原始特征表示的意义[7-8]. 随后有学者提出了基于群智能算法的图像特征选择方法， 如遗传算法、 粒子群优化算法等[9-10]， 它们根据特征对图像分类结果的贡献给每一个特征赋予一个权值， 成为主要图像特征选择算法， 然而传统群智能算法存在一定的缺陷， 如局部最优， 对后继图像分类结果产生不利影响[11]. 当前图像分类器主要采用神经网络、 支持向量机等进行构建[12-13]， 神经网络要求训练样本大、 支持向量机， 存在学习效率低等不足. 相关向量机是一种新发展起来的机器学习算法， 解决了神经网络要求训练样本大， 避免了支持向量机学习效率低等缺陷， 为图像分类器的构建提供了一种新的工具[14].

2 PSO-RVM 的图像分类原理

基于PSO-RVM的图像分类模型工作原理为： 首先提取图像的颜色和纹理特征， 并进行归化一化处理， 然后采用混沌粒子群优化(CPSO)算法确定特征的相应权值， 最后采用RVM构建图像分类器， 具体如图 1 所示.

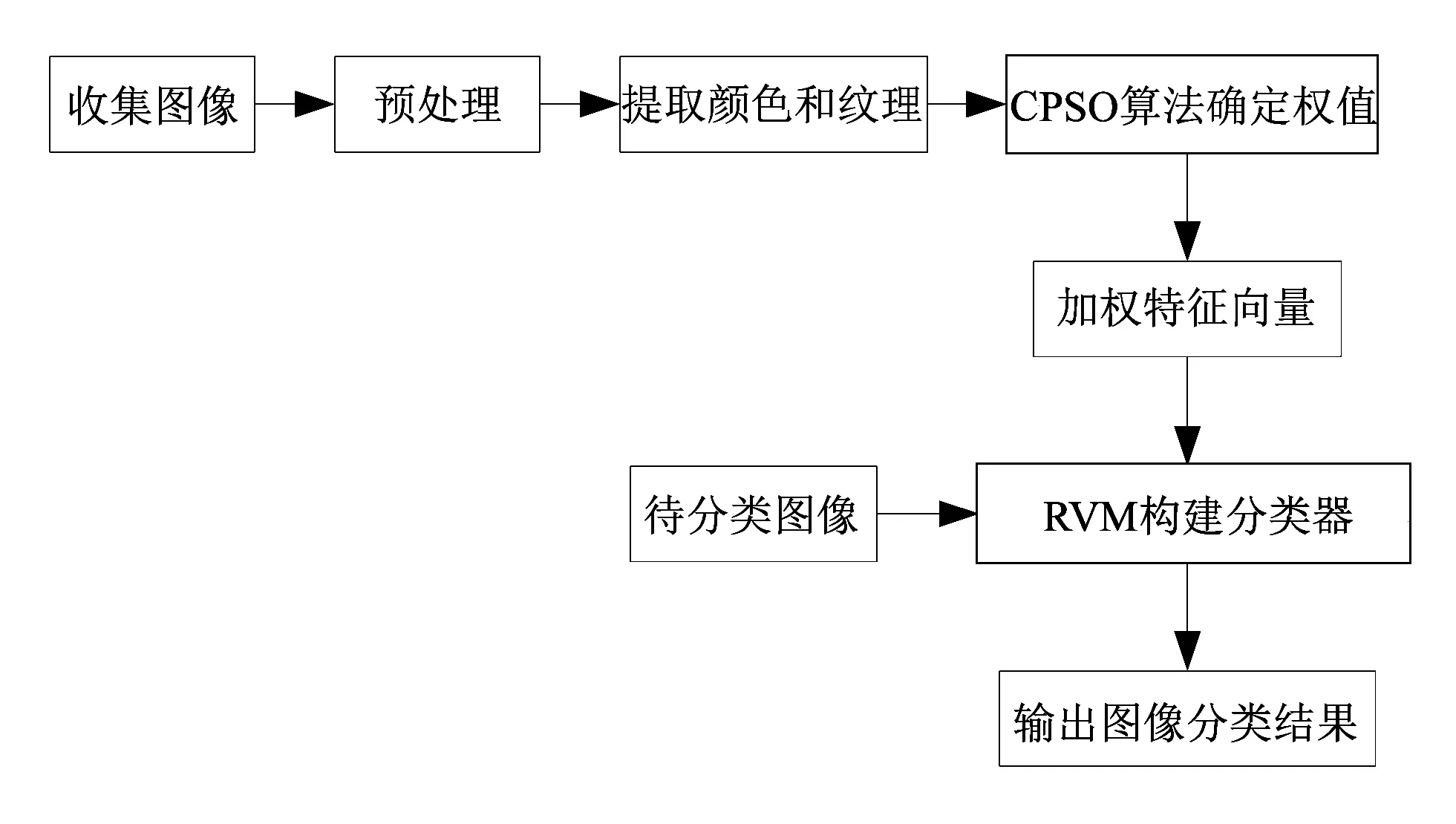
图 1 PSO-RVM的图像分类原理Fig.1 Principle of PSO-RVM image classification

3 PSO-RVM的图像分类模型

3.1 提取图像特征

3.1.1 提取图像的纹理特征

纹理是一种重要的图像特征， 可以描述图像中反复出现的局部模式和排列规则， 其中灰度共生矩阵是一种常用的图像纹理特征提取算法. 灰度共生矩阵表示两个像素同时出现的概率(P(i,j,d,θ))， 其计算公式为

P(i,j,d,θ)=

{[(x,y),(x+dx,y+dy)|f(x,y)=i,

式中：x，y是像素的坐标；i，j是灰度值； dx， dy是位置偏移量；d是像素间的距离；θ为灰度共生矩阵的生成方向.

Haralick等定义了14个灰度共生矩阵特征参数， 通过对图像的纹理分析研究， 结果表明， 在14个灰度共生矩阵的纹理特征中， 仅有4个特征是不相关的， 为此， 本文采用该4个特征描述图像的纹理特征.

1) 角二阶矩(ASM). 角二阶矩是图像灰度分布均匀性的度量， 纹理粗时ASM值大， 纹理细时ASM值小， 其定义如下

2) 惯性矩(CON). 惯性矩反映了图像的清晰度， 纹理沟纹深时CON值大， 效果清晰， 纹理沟纹浅时CON值小， 效果模糊， 其定义如下

3) 熵(ENT). 熵是图像所具有的信息量的度量， 若图像没有任何纹理， 则ENT值几乎为0， 纹理复杂时ENT值大， 纹理简单时ENT值小， 其定义如下

(4)

4) 相关性(COR). 相关性反应灰度共生矩阵的元素在行方向或列方向的相似度， 其定义如下

分别统计角二阶矩、 惯性矩、 熵、 相关性4个参量在0°, 45°, 90°, 135°方向上的值， 将角二阶矩、 惯性矩、 熵、 相关性的均值和方差共8个量作为纹理特征.

3.1.2 提取图像的颜色特征

颜色是一种非常稳定的图像特征， 其中颜色矩是一种简单有效的颜色特征描述方法， 由于颜色信息主要分布于低阶矩中， 因此， 提取图像的一阶矩和二阶矩作为颜色特征. 设i通道的第j个像素为pij，N为像素总数， 每一个颜色通道的一阶矩和二阶矩计算公式分别为

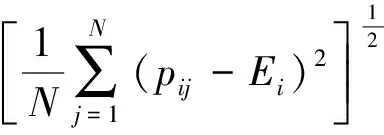
3.2 混沌粒子群优化算法

3.2.1 标准粒子群优化算法

Kennedy等通过对模拟鸟群觅食进行分析， 提出了PSO算法， 假设待求解问题的搜索空间为D维， 第i个粒子的当前最优解为pbest， 整个群体的全局最优解为gbest， 每次迭代， 粒子的位置和速度的更新公式为

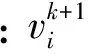
3.2.2 粒子群优化算法的混沌机制

针对标准PSO算法存在早熟收敛、 易于陷入局部极值、 解的精度低等问题， 将混沌系统引入到PSO算法中， 首先利用混沌序列对粒子位置进行初始化， 提高种群的多样性， 选择最优的初始种群； 然后在粒子群搜索过程中， 对最优位置进行混沌处理， 把混沌序列中的最优位置粒子代替当前粒子群中一个粒子的位置， 这样在迭代中产生局部最优解的许多邻域点， 加快找到最优解的速度.

Logistic混沌映射是一种经典的混沌系统， 其定义如下

式中：μ表示控制参数[15].

令xk是通混沌运算映射到[0,1]区间后的向量，βk为迭代k次后的混沌向量， 则施加了随机扰动后的混沌向量xk+i可以表示为

3.3 混沌粒子群优化算法确定权值

1) 采集图像， 提取颜色和纹理共10个特征， 并对该10个特征进行归一化处理， 组合得到图像分类的特征向量集.

2) 设置PSO算法的相应参数， 主要包括： 最大的迭代次数tmax， 惯性权重ω， 学习因子c1、c2， 混沌扰动范围等.

3) 随机产生一个10维分量的向量， 向量的值在[0 1]范围内， 该10维向量分别表示10个特征向量的权值， 采用Logisic映射产生N个初始种群向量， 从N个初始群中选择性能最好的M个解组成初始粒子群， 随机初始化速度.

4) 评价每个粒子的适应度， 如果粒子适应度fi优于pbest和gbest， 则更新pbest和gbest.

5) 更新粒子的位置和速度.

6) 根据Logistic混沌产生混沌序列， 并将其通过逆映射， 返回到原解空间， 在原解的空间对每个可行解计算其适应度值fi， 得到性能最好的可行解， 用性能最好的可行解替代当前群体中粒子的位置.

7) 判断是否满足条件， 若满足则停止， 输出最优位置， 即10个特征向量的最优权值.

3.4 构建图像分类器

式中：ωi为噪声.

通过核函数K(x,xi)的线性组合形式描述RVM， 即

(12)

式中：w=[w0,w1,…,wN]T为权值向量.

RVM的概率模型可以描述为

(13)

引入超参数β， 整个训练样本数据组的似然函数表示为

p(t|

式中：t=[t0,t1,…,tN]T.

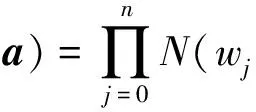
式中：a=[a0,a1,…,aN]T为超参数.

根据贝叶斯公式即可得到w后验分布的数学表达式

p(w|

式中：p(w|a)与p(t|w,β)皆为高斯分布.

p(t|a,β)中不含有w, 则可将其看作一个系数， 因此可写为

p(w|t,a,a)=N(w|

式中：Σ是协方差矩阵；μ是均值向量， 它们分别为

其中，A=diag(a0,a1,…,aN).

w的后验分布必须对β和aj进行优化， 可得到aj和β的计算公式

其中，μj为μ的第j个元素，Σjj是矩阵Σ的第j个对角元.

对于新输入的一组数据x*， 对应输出为t*,

t*=φ(x*)μ.

4 仿真实验

4.1 数据来源

为了测试PSO-RVM图像分类模型的有效性， 在Intel® Core(TM) i5-2450M 2.85 GHz CPU， 4 GB RAM， Windows 7 操作系统， Matlab 2013环境下仿真实验. 数据来源于标准图像分类试数据库： Pascal VOC 2012， 该数据库包含20类彩色图像， 具体为： 鸟、 猫、 奶牛、 狗、 马、 绵羊、 飞机、 自行车、 船、 公交车、 小汽车、 摩托车、 火车、 瓶子、 椅子、 餐桌、 盆景、 沙发和电视与显示器， 共计11 540个图像. 本文选择鸟、 狗、 飞机、 瓶子、 盆景等5类图像作为仿真对象.

4.2 结果与分析

4.2.1 与其它特征提取算法的性能对比

为提高CPSO算法选择特征的优越性， 采用主成分分析算法(PCA)、 遗传算法(GA)、 标准粒子群算法(PSO)进行对比实验， 其PCA选择累计贡献率为90%的向量， 而GA、 PSO、 CPSO算法通过确定特征权选择特征向量， 所有分类器均采用RVM构建， 每一种算法均运行10次实验， 它们的平均分类正确率如图 2 所示.

图 2 不同特征选择算法的平均分类正确率对比Fig.2 Comparison of average classification accuracy for different feature selection algorithms

从图 2 可以看出： 相对于PCA算法， GA、 PSO、 CPSO算法的平均分类正确率均得到一定的提高， 这主要是因为PCA算法是一种线性特征提取算法， 而图像受到光照等外界因素的影响， 特征之间不是简单的线性变化关系， 同时PCA算法是对特征融合和降维， 丢失了部分有用信息， 而GA、 PSO、 CPSO算法为确定特征权值， 通过特征权值确定每一个特征对图像分类结果的作用， 可以获得更加理想的图像分类效果.

4.2.2 与其它分类器的性能对比

为了测试RVM构建图像分类器的优越性， 采用最近邻算法(KNN)、 支持向量机(SVM)、 BP神经网络(BPNN)构建分类器进行对比实验， 所有特征的权值采用CPSO算法进行确定， 每一种模型均运行10次实验， 统计它们平均分类的正确率， 结果如图 3 所示.

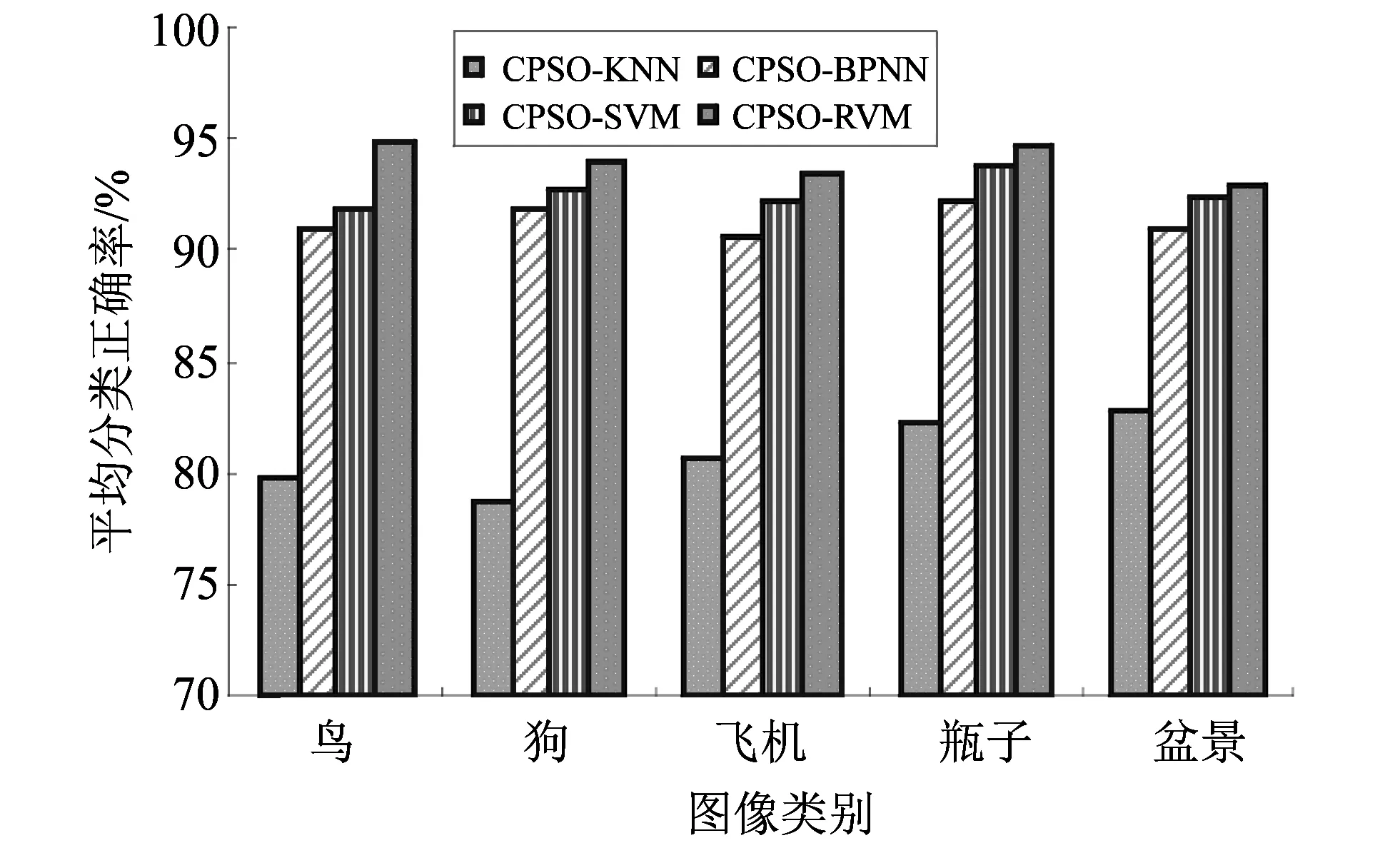
图 3 不同分类器的平均分类率对比Fig.3 Comparison of average classification accuracy of different classifiers

从图 3 可知， 相对于其它图像分类器， RVM的分类正确率最高， 这主要是由于RVM具有更优的非线性学习和泛化性能， 构建的图像分类器可以更加准确地描述图像特征向量与图像类别之间的非线性映射关系， 因此RVM提高了图像分类的正确率， 降低了图像的误分率.

4.2.3 不同模型的分类速度对比

速度也是评价图像分类模型的一个有意义指标， 所有模型的图像平均分类时间如表 1 所示.

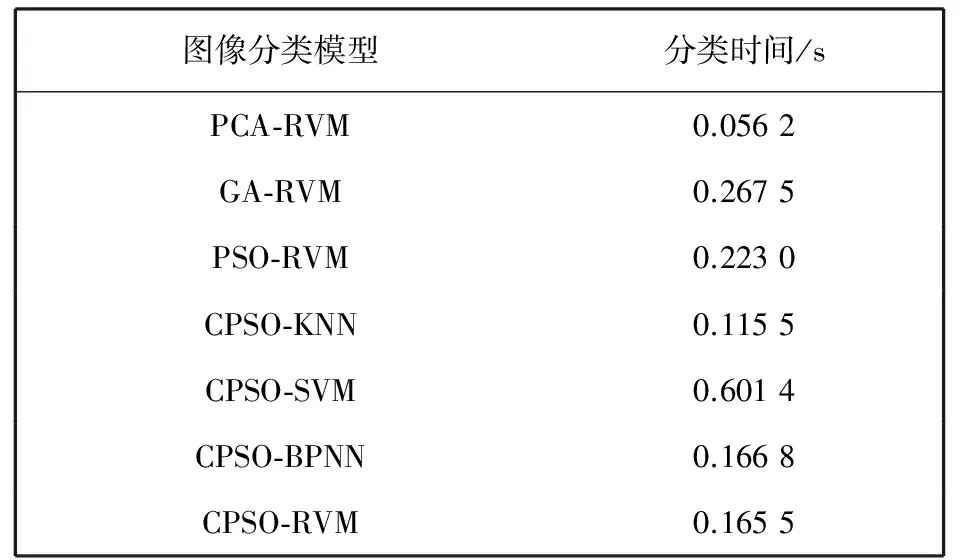
表 1 不同模型的平均分类时间对比

从表 1 可知， 相对于PCA算法， GA、 PSO、 CPSO算法的平均分类时间相对较高， 但是PCA算法的分类正确率太低， 不能满足图像管理实际应用要求， 相对于GA、 PSO算法， CPSO算法的分类速度得到提高， 可以很好地满足网络图像分类的在线要求. 同时SVM、 BPNN， RVM的分类速度也得到加快， 虽然KNN 分类速度最快， 但存在分类正确率低， 错误差高的缺陷， 因此PSO-RVM的图像分类综合性能最优.

5 结 语

为了获得更好的图像分类结果， 结合CPSO算法和RVM的优点， 提出一种混沌粒子群算法优化特征值的的图像分类模型. 仿真实验结果表明， 该模型加快了图像分类的速度， 提高了图像的分类正确率， 可以满足图像分类的实际应用需求.

[1]Lu D, Weng Q. A survey of image classification methods and techniques for improving classification performance[J]. International Journal of Remote Sensing, 2007, 28(5)： 823-870.

[2]刘丽, 匡纲要. 图像纹理特征提取方法综述[J]. 中国图像图形学报， 2009， 14(4)： 623-635. Liu Li， Kuang Gangyao. Overview of image textural feature extraction methods[J]. Journal of Image and Graphics， 2009， 14(4)： 623-635. (in Chinese)

[3]杨关， 冯国灿， 陈伟福， 等. 纹理分析中的图模型[J]. 中国图象图形学报， 2011， 16(10)： 1818-1825. Yang Guan， Feng Guocan， Chen Weifu， et al. Graphical models in texture analysis[J]. Journal of Image and Graphics， 2011， 16(10)： 1818-1825. (in Chinese)

[4]陈凯， 肖国强， 潘珍， 等. 单尺度词袋模型图像分类方法[J]. 计算机应用研究， 2011， 10(28)： 3986-3988. Chen Kai， Xiao Guoqiang， Pan Zhen， et al. Single-scale image classification employing Bag-of-Words model[J]. Application Research of Computers， 2011， 10(28)： 3986-3988. (in Chinese)

[5]Zhang B C， Gao Y S， Zhao S Q， et al. Local derivative pattern versus local binary pattern： face recognition with high-order local pattern descriptor[J]. IEEE Transactions on Image Processing， 2010， 19(2)： 533-544.

[6]张刚， 马宗民. 一种采用Gabor小波的纹理特征提取方法[J]. 中国图像图形学报， 2010， 15(2)： 248-254. Zhang Gang， Ma Zongmin. An approach of using gabor wavelets for texture feature extraction[J]. Journal of Image and Graphics， 2010， 15(2)： 248-254. (in Chinese)

[7]王向阳， 杨红颖， 郑宏亮， 等. 基于视觉权值的分块颜色直方图图像检索算法[J]. 自动化学报， 2010， 36(10)： 1489-1492. Wang Xiangyang， Yang Hongying， Zheng Hongliang， et al. A color block-histogram image retrieval based on visual weight[J]. Acta Automatica Sinica， 2010， 36(10)： 1489-1492. (in Chinese)

[8]李大湘， 彭进业， 贺静芳. 基于EMD-CkNN多示例学习算法的图像分类[J]. 光电子·激光， 2010， 21(2)： 304-306. Li Daxiang， Peng Jinye， He Jingfang. Image categorization based on EMD-CkNN multi-instance learning algorithm[J]. Journal of Optoelectronics Laser， 2010， 21(2)： 304-306. (in Chinese)

[9]杜娟， 孙君顶. 基于特征加权和支持向量机的图像分类研究[J]. 激光与红外， 2013， 43(3)： 315-318. Du Juan， Sun Junding. Image classification based on feature weighting and support vector machine[J]. Laser & Infrared， 2013， 43(3)： 315-318. (in Chinese)

[10]刘一鸣. 自适应量子行为粒子群算法及其在图像分类中的应用研究[D]. 杭州： 浙江大学， 2011.

[11]Jiang S H， Chen B F. Method of image retrieval based on integrating low level feature with relevance feedback[J]. Machine Building and Automation， 2009， 38(3)： 51-53.

[12]刘亚楠， 涂铮铮， 罗斌. 基于加权高阶奇异值分解的支持张量机图像分类[J]. 微电子学与计算机， 2014， 31(5)： 28-31. Liu Yanan， Tu Zhengzheng， Luo Bin. Support tensor machine image classification based on weighted high-order singular value decomposition[J]. Microelectronics & Computer， 2014， 31(5)： 28-31. (in Chinese)

[13]谢文兰， 石跃祥， 肖平. 应用BP神经网络对自然图像分类[J]. 计算机工程与应用， 2010， 46(2)： 163-166. Xie Wenlan， Shi Yuexiang， Xiao Ping. Classification of natural image based on BP neural network[J].Computer Engineering and Applications， 2010， 46(2)： 163-166. (in Chinese)

[14]柳长源， 毕晓君， 韦琦. 基于相关向量机的含噪声人脸图像识别[J]. 吉林大学学报(工学版)， 2013， 43(4)： 1121-1125. Liu Changyuan， Bi Xiaojun， Wei Qi. Noisy face images recognition based on relevance vector machine[J]. Journal of Jilin University (Engineering and Technology Edition)， 2013， 43(4)： 1121-1125. (in Chinese)

[15]高雷阜， 刘旭旺. 一种基于混沌的自适应粒子群全局优化方法[J]. 计算机工程与应用， 2010， 46(3)： 51-53. Gao Leifu， Liu Xuwang. Adaptive particle swarm global optimization algorithm based on chaos[J]. Computer Engineering and Applications， 2010， 46(3)： 51-53. (in Chinese)

Image Classification Algorithm Based on Optimal Feature Weighting

WANG Yu-jing

(Dean’s Office of Aba Teachers University, Wenchuan 623002, China)

This article focuses on the problem of feature selection and classifier construction in the image classification process. An image classification algorithm based on optimal feature weighting was proposed. Firstly, collect the color and texture feature of images. Secondly, calculate the weights of each feature using chaotic particle swarm optimization algorithm, where the weights represents contributions of correspond feature to the classification model is determined. Finally, the weighted vector sample set is studied by the relevant vector machine, and then construct the classifier to achieve the image classification. Experiment results show that the proposed algorithm not only can improve the accuracy of image classification, but also reduce the classification time, which means that it has a certain practical value compared with the popular image classification model.

image classification; features selection; particles swarm optimization algorithm; relevance vector machine

2016-08-23

四川省教育厅重点科研资助项目(15ZA0339)； 阿坝师范学院校级科研基金资助项目(ASC15-20)

王玉晶(1982-)， 女， 讲师， 硕士， 主要从事模式识别、 智能算法的研究.

1673-3193(2017)02-0196-06

TP391

A

10.3969/j.issn.1673-3193.2017.02.018