新型卡铁偏转式闭锁机构设计与动力学仿真

孙艳馥， 李回滨， 闫 雷， 郭光全， 吕慧贞

(1. 沈阳理工大学 装备工程学院， 辽宁 沈阳 110159； 2. 山东特种工业集团， 山东 淄博 255201；3. 晋西工业集团有限责任公司， 山西 太原 030051)

新型卡铁偏转式闭锁机构设计与动力学仿真

孙艳馥1， 李回滨1， 闫 雷2， 郭光全3， 吕慧贞3

(1. 沈阳理工大学 装备工程学院， 辽宁 沈阳 110159； 2. 山东特种工业集团， 山东 淄博 255201；3. 晋西工业集团有限责任公司， 山西 太原 030051)

通过对闭锁机构工作特性的分析， 在12号霰弹的基础上， 设计了一款新型的卡铁偏转式闭锁机构. 利用UG软件对所设计的机构进行三维建模， 以闭锁块为研究对象， 通过动力学分析建立了闭锁机构动力学微分方程， 并运用ADAMS对模型进行仿真. 仿真结果表明： 闭锁机构能在0.5 s内完成开锁， 在1 s内完成闭锁； 后坐与复进的运动特性证明闭锁机构运动协调、 闭锁可靠并能复进到位. 所建立的卡铁偏转式闭锁机构动力学微分方程， 为自动武器闭锁机构的设计提供了一定的理论依据.

卡铁； 偏转式； 闭锁机构； 动力学

0 引 言

闭锁机构按照发射时身管与枪机的联接性质分为惯性闭锁和刚性闭锁两大类[1]. 惯性闭锁机构闭锁时身管和枪机无扣合或在壳机力作用下能自行开锁. 刚性闭锁机构闭锁时身管和枪机可牢固扣合， 射击时壳机力不能使枪机直接开锁， 必须在主动件强制作用下才能开锁， 这类闭锁机构工作可靠， 被广泛采用. 由于卡铁偏转闭锁机构由成对的开锁工作面、 闭锁工作面和闭锁支撑面等组成， 开闭锁动作分别在开闭锁工作面的相互作用下完成， 壳机力也作用在闭锁支撑面上， 因而这种闭锁机构开闭锁动作可靠， 安全系数高， 所以在半自动泵动式霰弹枪中能够发挥重要作用. 国内对于轻武器闭锁机构进行了多方面的研究， 如文献[2]对机头回转式闭锁机构建立了运动分析模型， 进行了运动特性仿真分析； 文献[3]对各种枪机闭锁机构的计算模型进行了梳理； 文献[4]运用有限元的方法对机头回转式闭锁机构进行了动应力分析； 文献[5]对枪机回转式闭锁机构开锁过程进行了运动分析； 文献[6]对枪管回转式闭锁机构进行了设计与动力学分析. 但目前对于偏转式闭锁机构的研究相对较少， 因而对卡铁偏转式闭锁机构进行动力学研究很有必要， 可以为卡铁偏转式闭锁机构的发展提供理论依据和技术手段， 对于提高武器的性能具有促进作用.

1 新型卡铁偏转式闭锁机构的设计

1.1 设计原理

卡铁偏转式闭锁机构工作时， 枪机框运动中靠斜面带动卡铁上下偏转一定角度， 使枪管与枪机之间完成开闭锁动作. 这种机构的闭锁支撑面在机匣两侧导轨上对称布置， 无附加力矩， 有利于提升精度， 是目前通过中间零件闭锁的诸结构中比较成功的一种[1]. 为了更好地发挥卡铁偏转闭锁方式的优势， 使得开闭锁动作灵活， 应尽量减少开闭锁过程中的能量消耗[7]， 且使闭锁机构结构简单、 工艺性好. 设计的新型卡铁偏转式闭锁机构工作原理图如图 1 所示.

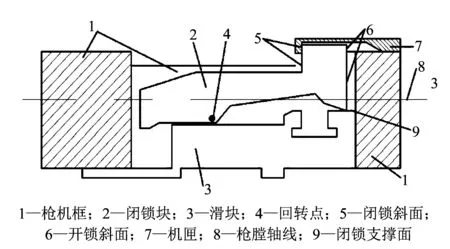
图 1 新型卡铁偏转闭锁机构原理图Fig.1 Schematic diagram of new locking mechanism of lock-iron deflection type

1.2 设计原则

闭锁机构的设计必须满足其设计要求， 才能达到武器装备的性能要求， 卡铁偏转式闭锁机构的结构设计要求主要有：

1) 闭锁机构应留出初始弹底间隙；

2) 在壳机力作用下不应自行开锁；

3) 应当避免或减小由楔紧引起的附加摩擦力；

4) 闭锁支撑面与身管轴线对称布置[8]；

5) 机构应尽量结构简单、 工艺性好、 可靠性高[9].

1.3 设计方法

选用12号霰弹进行闭锁机构设计， 其外形呈圆柱形， 直径18.4 mm， 弹长72 mm， 单发弹重25.6 g. 以该参数为设计依据， 运用偏转式闭锁工作原理进行设计. 基于UG软件对设计的枪机框、 滑块、 闭锁块、 枪机等实现三维建模， 其模型如图 2～图 5 所示.

图 2 枪机框Fig.2 Bolt carrier

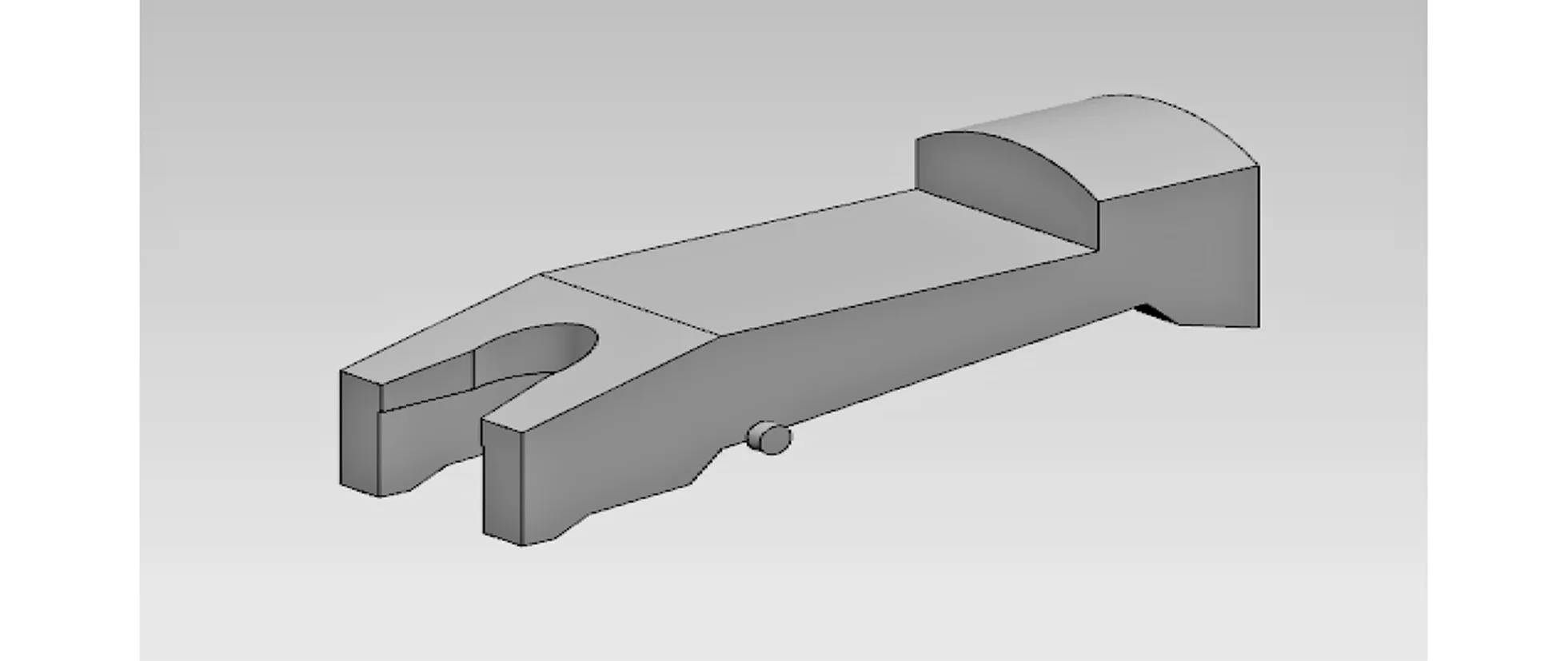
图 3 闭锁块Fig.3 Locking block

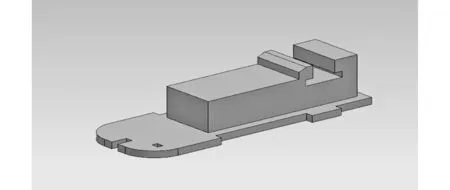
图 4 滑块Fig.4 Slide

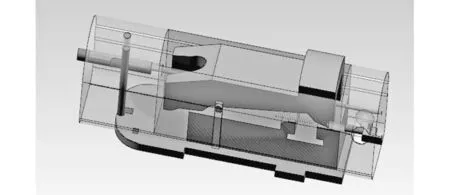
图 5 枪机Fig.5 Bolt

由于霰弹的长度为72 mm， 所设计的枪机框的长度必将大于霰弹的长度以实现枪机框可以基本上遮盖抛壳窗， 并且枪机框的整体宽度为20 mm， 高度为24.2 mm， 与霰弹底部的面积相比较大， 可以稳固地将霰弹抵住， 防止霰弹底部因受力不均影响弹丸的发射与枪械的稳定.

闭锁块配合于枪机框内部， 闭锁块总长为46 mm， 宽为14 mm； 闭锁部分长为10 mm， 可以保证有足够的刚度以避免闭锁不可靠； 闭锁部分比其余部分略高以实现与枪管的配合； 闭锁块下部分的轮廓形状与滑块相配合.

滑块作为一个载体承载着枪机框与其相关的部件， 而且主导了开闭锁的运动. 滑块的总长为63 mm， 总宽为23 mm， 高度为14 mm， 滑块前端部分的上沿将与闭锁块的闭锁支撑面接触， 闭锁块的旋转位移由滑块的高度决定. 而滑块的凸起部分应和闭锁块相同， 与枪机框接触， 如此， 当滑块运动时， 枪机框能与滑块配合只进行前后方向的运动， 左右方向被限制而不会发生位移， 这样也保证击针的位置使击针只会前后运动， 降低了枪弹击发故障率.

闭锁机构与击针组件、 抽壳机构共同组成了枪机， 构成了枪械的核心部件， 共同完成复进、 闭锁、 击发、 后坐、 开锁等工作循环.

2 动力学仿真

2.1 数学模型建立

为了便于分析， 在忽略一些次要影响因素的基础上建立闭锁机构动力学模型， 模型的建立需作以下几点假设：

1) 认为闭锁机构各构件是规则的， 且各构件质心分布均匀；

2) 忽略闭锁时闭锁块与机匣以及滑块之间碰撞产生的影响；

3) 认为射击时整枪保持水平， 不受重力分力影响.

据以上假设， 闭锁机构工作时的受力情况如图 6 所示.

图 6 卡铁偏转闭锁机构受力分析图Fig.6 Stress analysis diagram of locking mechanism of lock-iron deflection type

由图 6 可知， 滑块作为基础构件作平移运动， 闭锁块作为工作构件作定轴转动. 基础构件滑块0在主动力F的推动下沿x方向作平移运动， 带动作用使定力矩为M1的工作构件1绕O1点作定轴转动， 根据牛顿第二定律， 可得两构件的运动微分方程如下

式中：m0为滑块质量；m1为闭锁块质量；Ff1为闭锁块与滑块之间摩擦力；Ff2为滑块与枪机框之间摩擦力；F为主动力；J1为闭锁块转动惯量；M1为阻力矩；FR为约束反力；MR1为约束反力矩；r为滑块转动力矩；φ1为滑块偏转角度；x为滑块平动位移.

2.2 仿真结果分析

利用ADAMS对闭锁机构进行动力学仿真， 仿真时间设置为1 s， 步长为1 000. 设置驱动函数为Step(time,0,0,0.5,90)+Step(time,0.5,0,1,-90)， 构件之间添加系统默认接触力， 设置霰弹枪材料均为Steel. 枪机框与闭锁块位移、 速度曲线对比图如图 7， 图 8 所示. 从图7知： 0.11 s时枪机框和闭锁块开始运动， 运动趋势平稳， 当0.89 s 时停止运动. 枪机框和闭锁块的运动趋势大致相同， 证明两者运动同步， 符合设计原理. 从图8知： 0.11 s时闭锁块开锁， 闭锁块速度产生突变， 枪机框被滑块带动， 速度在瞬间增大， 0.89 s 时闭锁块复进到位准备闭锁， 在0.89～1 s内开始上弹， 此时枪机框受到外力作用而产生速度的瞬变， 闭锁块由于闭锁支撑面的作用也产生迅速变化. 由图 7， 图8可知， 闭锁块偏转开锁和闭锁的时间为0.11 s和0.89 s， 且能在0.5 s内完成开锁， 在1 s内完成闭锁. 仿真结果表明开、 闭锁机构作用可靠， 可正常工作.

图 7 枪机框与闭锁块位移曲线对比图Fig.7 Displacement curve diagram of bolt carrier compared with lock-iron

图 8 枪机框与闭锁块速度曲线对比图Fig.8 Velocity curve diagram of bolt carrier compared with lock-iron

3 闭锁机构运动特征分析

闭锁机构工作循环方式对武器性能有很大影响. 它描述了基础构件的工作顺序和各机构的运动关系， 可作为机构是否可靠、 协调， 射击频率、 后坐阻力等是否满足要求的依据. 工作循环方式的制定是以基础构件的位移或时间为自变量来制作的[6]. 表 1 是闭锁机构射击时各部件的运动情况一览表： 后坐时， 前端与枪机框一起后坐， 枪机框后坐10 mm为自由行程， 闭锁块不发生偏转， 滑块后坐10 mm后坐到位， 并开锁， 滑块继续后坐， 枪机抽弹， 套筒后坐60 mm时抛出弹壳， 之后枪机后坐到位； 复进时套筒复进20 mm后推弹， 复进30 mm时枪机推弹入膛， 与滑块一起复进过程中完成闭锁， 最后复进到位. 闭锁机构运动特性满足了设计原理[10]， 说明闭锁机构设计合理， 可保证开闭锁过程可靠工作.

表 1 闭锁机构射击时各部件的运动情况一览表[11]

4 结 论

通过对卡铁偏转式闭锁机构的设计、 建模、 动力学研究以及ADAMS仿真可得出如下结论：

1) 证明了所设计的闭锁机构可以可靠地在0.5 s 内完成开锁， 在1 s内完成闭锁的功能.

2) 闭锁机构的基础构件的工作顺序和运动关系也有效地证明机构作用可靠、 运动协调、 射击频率满足要求.

3) 运动学分析所得到了闭锁机构动力学微分方程为闭锁机构的设计提供了一定的理论依据， 具有一定的指导意义.

[1]薄玉成， 王惠源， 李强， 等. 自动机结构设计[M]. 北京： 兵器工业出版社. 2009.

[2]黄怀宇. 某反器材武器闭锁机构分析研究[D]. 南京： 南京理工大学， 2010.

[3]姜迪. 自动武器设计计算模型与软件研究[D]. 南京： 南京理工大学， 2015.

[4]葛藤， 赵军， 周克栋. 某新型自动步枪闭锁机构动应力分析[J]. 弹道学报， 2006, 18(2)： 36-39. Ge Teng, Zhao Jun, Zhou Kedong. Analysis of dynamic stress of a new rifle locking mechanism[J]. Journal of Ballistics, 2006, 18(2)： 36-39.(in Chinese)

[5]王金梅， 张清. 回转闭锁机构开锁过程的运动分析[J]. 华北工学院学报， 1996， 17(1)： 90-94. Wang Jinmei， Zhang Qing. Motion analysis of unlocking course of rotary breech-action[J]. Journal of North China Institute of Technology， 1996， 17(1)： 90-94. (in Chinese)

[6]梁振刚， 韩铁， 袁志华， 等. 回转式枪自动机结构动力学仿真研究[J]. 火力与指挥控制， 2015， 40(10)： 183-186. Liang Zhengang， Han Tie， Yuan Zhihua， et al. Dynamic simulation research on the structure of revolving pistol automatic[J]. Fire Control & Command Control， 2015， 40(10)： 183-186. (in Chinese)

[7]张伟， 姚养无. 枪机回转式闭锁机构开锁能量损失分析[J]. 华北工学院学报， 1999， 20(3)： 252-255. Zhang Wei， Yao Yangwu. The analysis on the energy consumption of the rotating-bolt locking mechanism[J]. Journal of North China Institute of Technology， 1999， 20(3)： 252-255. (in Chinese)

[8]杨卓. 链式机枪自动机设计及仿真研究[D]. 太原： 中北大学， 2015.

[9]代程. 某多功能发射装置的建模和仿真分析[D]. 南京： 南京理工大学， 2013.

[10]王宇建， 崔艳国， 张军挪， 等. 某重机枪闭锁机构与常见故障间的关系分析[J]. 兵工自动化， 2006， 25(7)： 42-43. Wang Yujian， Cui Yanguo， Zhang Junnuo， et al. Analysis for locking mechanism of certain heavy scatter-gun and relations of common faults[J]. Ordnance Industry Automation， 2006， 25(7)： 42-43. (in Chinese)

[11]靳通. 某迁移式自动机的设计与仿真研究[D]. 南京： 南京理工大学， 2013.

Design and Dynamic Simulation of the New Locking Mechanism of Lock-Iron Deflection Type and Dynamic Simulation

SUN Yan-fu1， LI Hui-bin1， YAN Lei2， GUO Guang-quan3， LÜ Hui-zhen3

(1. School of Equipment Engineering, Shenyang Ligong University, Shenyang 110159, China；2. Shandong Special Industries Group, Zibo 255201, China； 3.Jinxi Industries Group Co. Ltd., Taiyuan 030051, China)

On the basis of the 12th canister, designed a new locking mechanism of lock-iron deflection type through the analysis of the working characteristics of the locking mechanism, to improve the research on the dynamics of the locking mechanism. Established the 3D model based on UG and selected locking block as the research object, established the dynamics differential equation of the locking mechanism through the dynamics analysis and made simulation on the model by using the ADAMS. The results show that the locking mechanism can be completed the unlock within 0.5 s and lock within 1 s, the motion characteristics of the recoil and reentry proved that the locking mechanism is coordinated, and the locking is reliable and can be repositioned. Dynamics differential equation of the locking mechanism of lock-iron deflection type provides a certain theoretical basis for the design of the automatic weapon locking mechanism.

lock-iron; deflection type; locking mechanism; dynamics

2016-08-17

孙艳馥(1971-)， 女， 副教授， 主要从事武器发射及弹药结构设计的研究.

1673-3193(2017)02-0145-05

TJ203+.2

A

10.3969/j.issn.1673-3193.2017.02.009