小波和余弦变换的电机轴承故障特征参数构造

原菊梅

(太原工业学院 自动化系， 山西 太原 030008)

小波和余弦变换的电机轴承故障特征参数构造

原菊梅

(太原工业学院 自动化系， 山西 太原 030008)

针对传统故障诊断特征参数的应用缺陷， 提出了一种小波和余弦变换的感应电机轴承故障特征参数提取方法. 首先， 根据感应电机轴承振动信号的特点选择合适的小波滤波器和信息代价函数， 并将感应电机轴承振动信号分解到各个不同的频域子空间； 然后， 基于离散余弦变换的频域能量聚集性对分解后的信号构造感应电机轴承故障特征参数， 并对实际感应电机轴承正常、 内圈故障、 外圈故障和滚珠故障4种状态的振动信号进行分析， 验证了所构造的特征参数能有效地实现电机轴承的早期故障检测与诊断； 最后， 与传统故障诊断特征参数方法进行了比较， 说明所提出的特征参数构造方法对于感应电机轴承早期故障的诊断优于传统故障诊断特征参数方法.

小波包； 离散余弦变换； 故障诊断； 电机； 轴承

振动信号分析法是目前最常用的轴承故障诊断方法之一. 振动信号的传统处理方法有通过相关函数、 充分统计量、 时域指数、 频域指数等直接分析测量信号， 提取诸如方差、 峭度、 功率谱重心指标等时频域特征值来检测故障的发生， 但是， 这些方法对于轴承早期故障的诊断效果都不理想. 近几年， 人工神经网络(Artificial Neural Networks， ANN)、 支持向量机(Support Vector Machine， SVM)、 模糊逻辑(Fuzzy Logic)和进化算法(Evolving Algorithms， EA)等各种智能化技术都已成功应用于机器状态的自动检测与诊断中， 很大程度上改善了故障诊断的可靠性和自动诊断程度[1]. 但是， 对于早期故障诊断问题仍没有得到很好地解决. 小波分析具有多尺度性和“数学显微”特性， 可以对信号实现多尺度分析， 并能提取信号的全局特征和局部特征， 在机械故障特征提取中具有独特的优势[2]， 受到广大故障诊断研究工作者的青睐. 唐贵基等[3]提出了一种基于小波包分析、 频带能量分析和包络分析相结合的轴承故障诊断方法. Konar P等[4]提出了应用小波和支持向量机对感应电机轴承故障进行检测的方法. 李健宝等[5]提出了一种结合小波包分解与自回归模型的故障特征提取方法. 赵志宏等[6]提出了一种基于小波包变换与样本熵的轴承故障诊断方法. 文献[7-9]研究发现离散小波变换在缩短计算时间和早期故障检测方面优于连续小波变换. Kumar等[10]利用神经网络研究离散小波分析对于轴承故障的检测能力， 指出离散小波分析对于感应电机状态检测过程中的原始数据降噪是十分有用的. Ghods A等[11]应用频域离散小波变换于随机模型， 该方法适用于更多的电机轴承故障情形， 特别是早期故障诊断.

本文基于正交小波包的信号分解功能， 将电动机的振动信号分解成相互正交的频率子空间， 然后， 对每个频率子空间借助离散余弦变换(Discrete Cosine Transform， DCT)的频域能量聚集性构造其故障特征参数， 从而实现电动机轴承的早期故障检测与诊断， 最后测试4种电动机轴承状态信号， 并与传统特征值的诊断结果进行比较， 结果表明， 所提出的方法具有更好的早期故障诊断效果.

1 正交小波包和信息代价函数的选择

1.1 正交小波包的空间分解及频域表现

与多分辨率分析方法不同， 正交小波包分解是用一对滤波器来实现信号的分解的， 它对信号的低频和高频部分同时进行分解， 且这种分解是无冗余无疏漏的， 其分解结果如图 1 所示[5-6].

图 1 小波包分解Fig.1 Wavelet packet decomposition

由图 1 可见， 对于任意给定的分解尺度j， 信号会被分解成2j个子空间， 这种分解过程可以表示为一个二进制结构树.

其中，A1反映了信号的概况，D1是信号的噪声分量，AA2也是信号的概况， 但比A1含有较小的噪声，DA2、AD2和DD2是哭声分量，AAA3是几乎不含哭声的信号的概况，DAA3、ADA3、DDA3、ADD3、DAD3、ADD3和DDD3都属于噪声分量. 可以看出， 信号被分解成各个不同频带的子信号.

1.2 小波滤波器和信息代价函数的选择

实验检测系统由Y90S-4 型三相感应电动机、 变频器、 压电式传感器、 电荷放大器、 传声器、 恒流源、 INV300F 智能信号采集处理分析仪和个人计算机组成. 实验模拟了电机驱动端轴承(型号为SKF6205)的内圈故障、 外圈故障、 滚珠点蚀和轴承正常4种轴承状态， 测量了该感应电动机的振动信号， 故障设置采用电火花加工单点损伤的方法， 损伤直径为0.18 mm， 深度为0.28 mm. 电机上测振点选择了5点， 分别装在电机两端的轴向、 垂直径向和水平径向上， 感应电动机运行在空载稳定运行状态下， 电机转速为 1 800 r/min， 采样频率为12 kHz. 实验中轴承的数据为内圈直径25 mm， 外圈直径52 mm， 厚度15 mm， 滚珠直径8.18 mm， 节径44.2 mm， 滚珠个数为9个， 依此可计算得内圈故障、 外圈故障和滚动体故障的特征频率分别为转速的5.42、 3.58和 4.71倍.

一般来说， 小波包的选择取决于信号本身的性质、 信号分解的目的和最佳原则的选择. 在运用振动信号进行故障诊断时， 信号中的冲击分量往往是故障的征兆， 这就要求小波函数具有较高的频率选择性， 也即要求小波函数的频域波形衰减要快， 变化要陡， 在时间域内要有丰富的波形变化， 而Daubechies(简称dbN)小波正好具有这样的特点， 并且是具有高阶消失矩的紧支集正交小波， 同时， 在所有已有的正交小波函数中， 对于给定阶数的消失矩， dbN小波具有最短的紧支集. dbN中的N表示db小波的阶次， 随着N的增大， 尺度函数和小波函数的支撑范围逐渐变宽. 根据各故障特征频率， N选为5， 分解层次选为3层即可以满足电机轴承故障频率的细化要求.

信息代价函数选用Shannon熵判据， 即令xi为信号x(t)在某一子空间正交基上的投影， 则定义

为x的Shannon熵.

2 正交小波包感应电机轴承故障特征提取

2.1 正交小波包感应电机轴承振动信号分解

利用1.2节中选择的db5正交小波和Shannon熵判据对实验所采集到的电机轴承正常、 内圈故障、 外圈故障和滚动体故障4种工况的振动信号进行三层正交小波包分解， Shannon熵判据按式(1)计算. 4种工况的振动信号分解结果如图 2 所示.

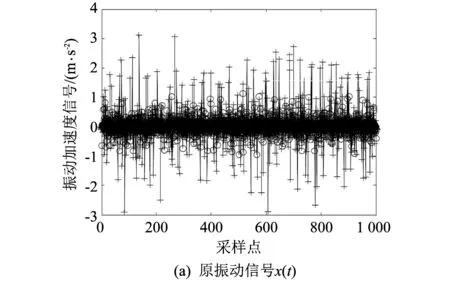
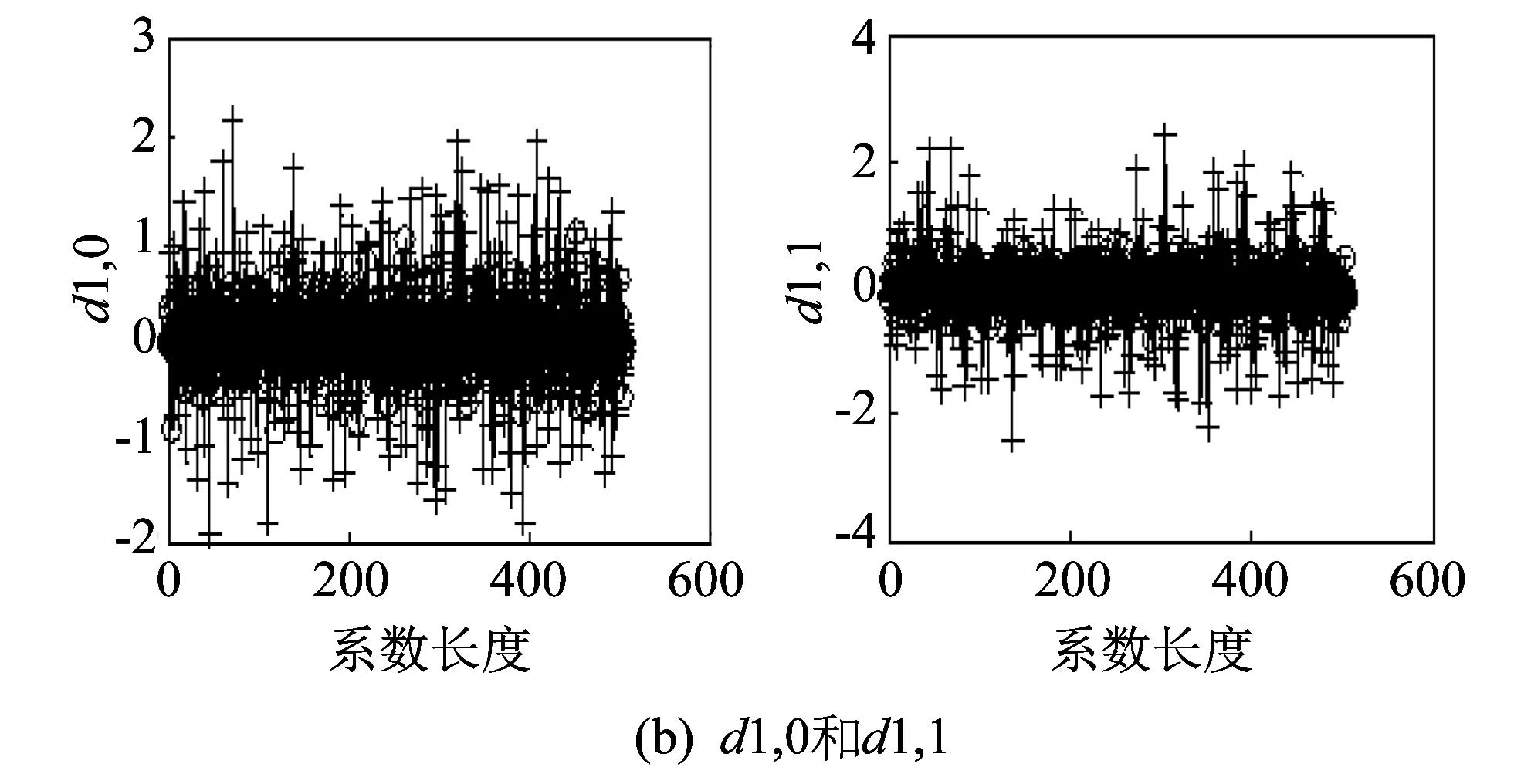
图 2 振动信号的小波包分解Fig.2 Vibration signal wavelet packet decomposition

图 2 中， 带三角形点的线条表示正常工况的振动信号分解结果， 带圈的线条表示外圈故障时振动信号的分解结果， 带加号的线条表示内圈故障时振动信号的分解结果， 带星号的线条表示滚珠故障时振动信号的分解结果. 可以看出， 在不同的节点上， 不同工况的变化是不同的.

2.2 频域能量聚集性的轴承故障特征参数构造

离散余弦变换具有很好的能量压缩性能[12]， 因此， 对2.1节中分解的每个子空间进行离散余弦变换， 得到各个子空间的离散余弦变换系数. 即数据长度为N的一维离散余弦变换定义为

k=0,1,2,…,N-1.

上述方程中的α(k)定义为

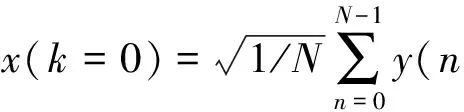
在此基础上， 构造故障特征参数为电机当前状态下各个子空间离散余弦变换系数2-范数相对于电机标准状态下各个子空间离散余弦变换系数2-范数的变化率. 即定义

式中：x为经小波包分解的每个子空间的离散余弦变换系数向量；i,j为小波包分解的二进制树节点；f,h分别表示电机轴承的失效和正常状态.

选择一组电机轴承正常工况时的振动加速度数据作为标准数据， 按式(2)计算各种工况的各个子空间的故障特征参数， 计算结果如图 3 所示.

由图 3 可以看出， 正常工况下的特征参数值都较小； 而3种故障状态下的特征参数相对于正常状态的变化都比较大， 且每种故障的8个特征参数变化是不同的， 彼此之间具有明显的差异.

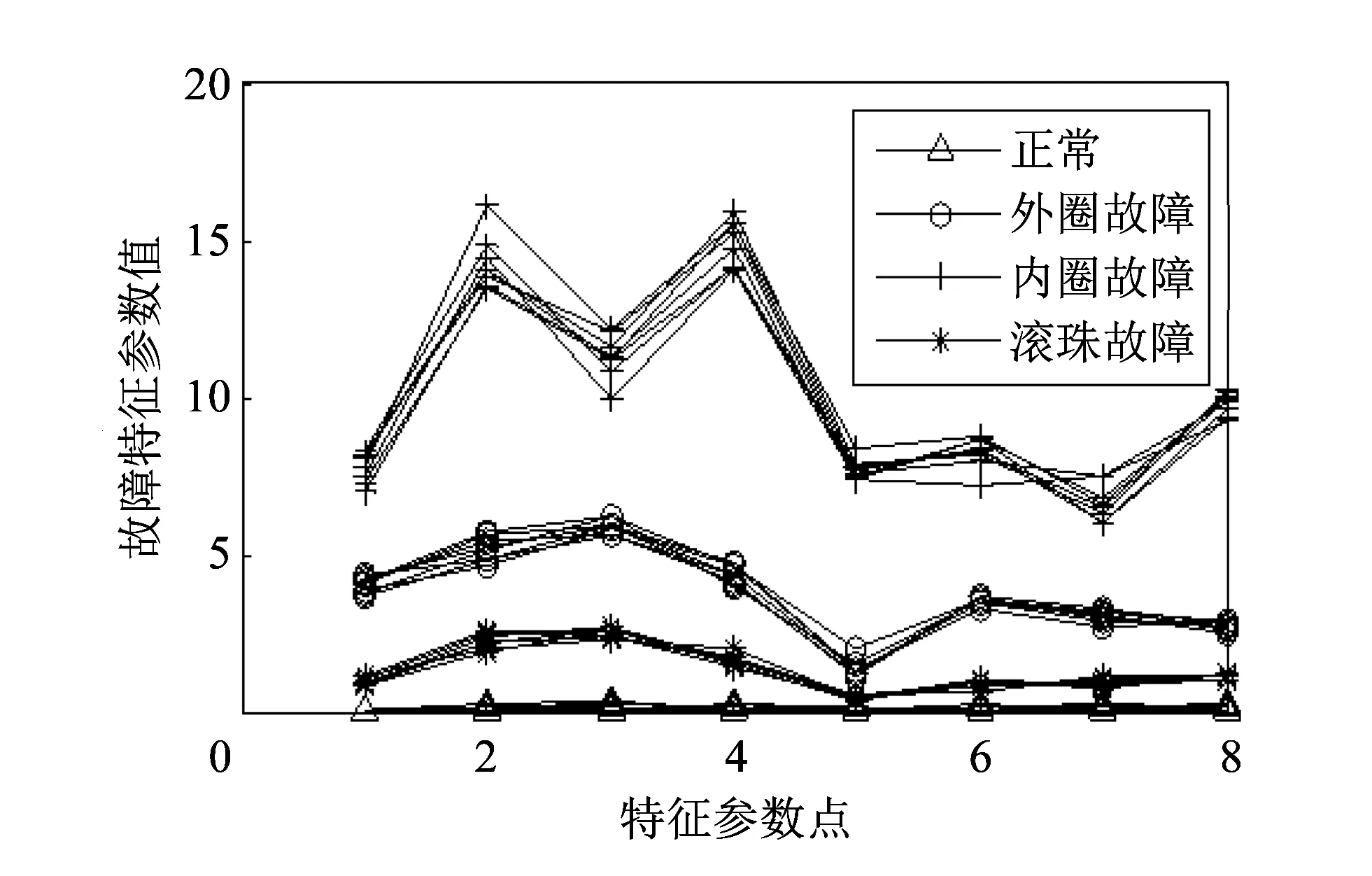
图 3 第种工况下各组数据的故障特征参数Fig.3 Fault feature parameters of every groups data under different conditions

2.3 基于特征参数的感应电机轴承故障诊断

对图 3 中的特征参数进行K均值聚类分析， 分别用欧氏距离和布洛克距离进行聚类分析， 分析结果如表 1 所示.

表 1 两种K均值聚类分类结果

由表 1 可以看出， 这两种距离都能正确分类电机轴承的4种工作状态.

3 与传统特征参数的比较

传统的故障诊断特征参数有时域参数和频域参数， 时域参数有峰值、 均值、 均方根值、 方根幅值、 标准差、 偏度、 峭度、 波形指标、 裕度指标和偏态指标等， 频域参数有频谱中心、 频域方差、 谐波因子和谱原点矩等. 对1.3节中采集到的电机轴承的内圈故障、 外圈故障、 滚珠点蚀和轴承正常4种状态的振动信号进行传统时域特征参数提取(选取常用的8个特征参数)， 处理结果如图 4 所示.

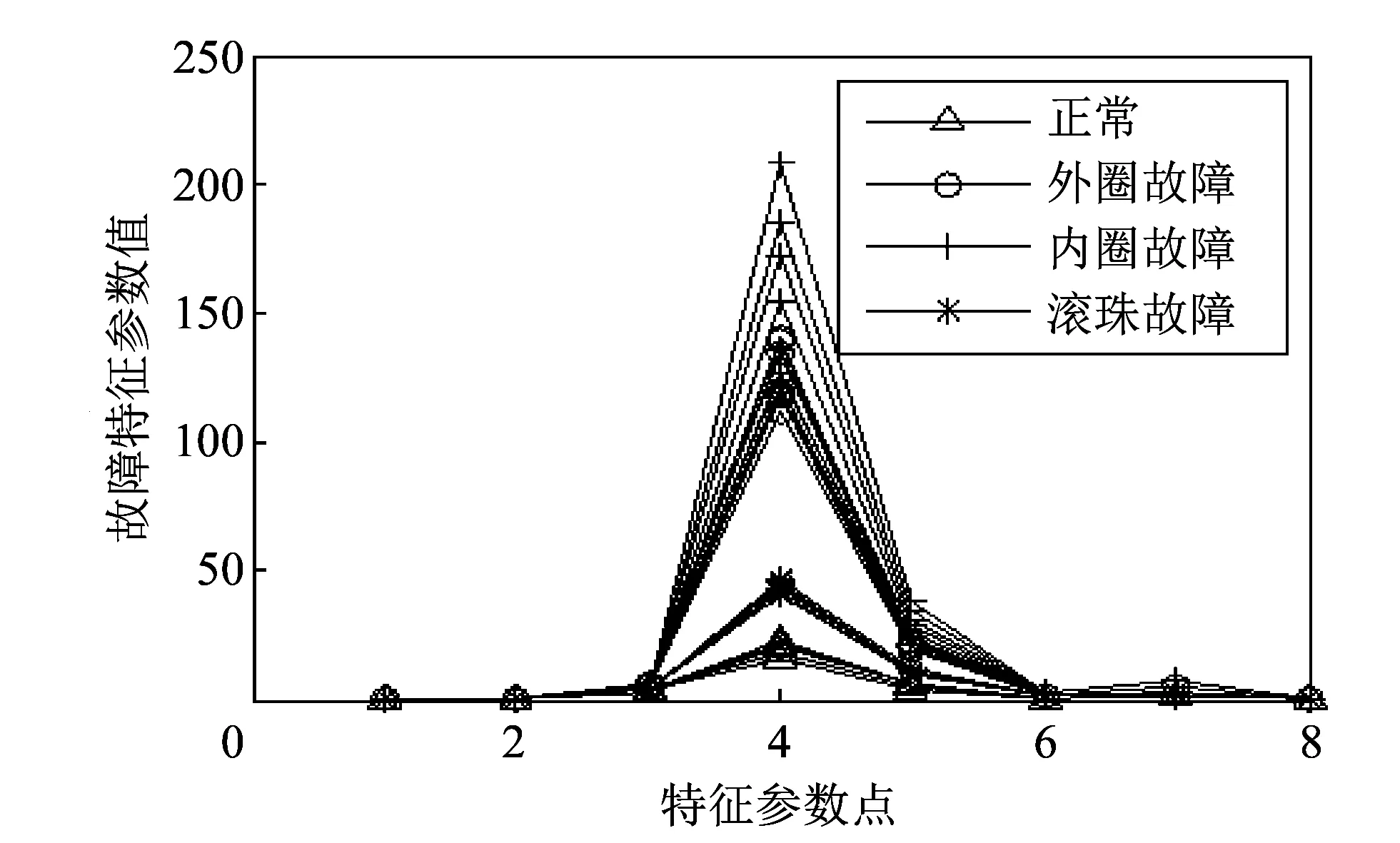
图 4 每种工况下的传统特征参数Fig.4 Tradition feature parameters of every groups data under different conditions

由图 4 可以看出， 这些传统的特征参数变化规律并不明显， 且4种工况间出现了重叠.

对图 4 中的传统特征值进行K均值聚类分析， 同样分别用欧氏距离和布洛克距离进行聚类分析， 分析结果如表 2 所示.

由表 2 可以看出， 这两种距离都不能完全正确的分类电机轴承的4种工作状态. 其中， 欧氏距离的误诊率为34.4%， 布洛克距离的误诊率为12.5%.

表 2 传统时域故障特征参数的两种K均值聚类分类结果

同样方法对采集到的电机轴承4种状态的振动信号进行传统频域特征参数提取并进行欧氏距离和布洛克距离聚类分析， 分析结果如表 3 所示.

表 3 传统频域故障特征参数的两种K均值聚类分类结果数

由表 3 可以看出， 完全无法正确分类电机轴承的4种工作状态.

由此可见， 对于传统的故障诊断特征参数需要采用其它较为复杂的智能方法进行分类分析才可以进行故障诊断. 说明传统特征参数不能直接用来进行电机轴承早期故障的诊断， 而此处提出的基于正交小波包分解的感应电机轴承特征参数提取方法可以用于电机轴承早期故障的诊断.

4 结 论

在对感应电机轴承振动信号进行正交小波包分解的基础上， 基于离散余弦变换的频域能量聚集性构造了感应电机轴承故障特征参数. 通过对感应电机轴承正常、 外圈故障、 内圈故障和滚珠故障4种工况的实测振动信号进行分析， 验证了所构造的特征参数能有效地实现电机轴承早期故障的检测与诊断. 并与传统特征参数方法进行了比较， 说明所提方法相对于传统特征参数方法更有效.

[1]Li B, Zhang P L, Tian H, et al. A new feature extraction and selection scheme for hybrid fault diagnosis of gearbox[J]. Expert Systems with Applications, 2011, 38(8)： 10000-10009.

[2]赵志宏， 杨绍普， 刘永强. 多小波系数特征提取方法在故障诊断中的应用[J]. 振动、 测试与诊断， 2015， 35(2)： 276-280. Zhao Zhihong， Yang Shaopu， Liu Yongqiang. Application of feature extraction method in fault diagnosis based on multi-wavelet coefficients[J]. Journal of Vibration， Measurement & Diagnosis， 2015， 35(2)： 276-280. (in Chinese)

[3]唐贵基， 蔡伟. 应用小波包和包络分析的滚动轴承故障诊断[J]. 振动、 测试与诊断， 2009， 29(2)： 201-204. Tang Guiji， Cai Wei. Rolling bearings fault diagnosis by using wavelet packetand envelope analysis[J]. Journal of Vibration， Measurement & Diagnosis， 2009， 29(2)： 201-204. (in Chinese)

[4]Konar P， Chattopadhyay P. Bearing fault detection of induction motor using wavelet and support vector machines[J]. Applied Soft Computing， 2011， 11(6)： 4203-4211.

[5]李健宝， 彭涛. 基于小波包参数模型的滚动轴承智能故障诊断[J]. 振动、 测试与诊断， 2012， 32(2)： 229-233. Li Jianbao， Peng Tao. Intelligent fault diagnosis of rolling bearing based on wavelet packet autoregressive model[J]. Journal of Vibration， Measurement & Diagnosis， 2012， 32(2)： 229-233. (in Chinese)

[6]赵志宏， 杨绍普. 基于小波包变换与样本熵的滚动轴承故障诊断[J]. 振动、 测试与诊断， 2012， 32(4)： 640-644. Zhao Zhihong， Yang Shaopu. Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J]. Journal of Vibration， Measurement & Diagnosis， 2012， 32(4)： 640-644. (in Chinese)

[7]Corral-Hernández J A， Antonino-Daviu J A. Influence of the start-up system in the diagnosis of faults in the rotor of induction motors using the discrete wavelet transform[J]. Procedia Computer Science， 2016， 83： 807-815.

[8]Yan R Q， Gao R X， Chen X F. Wavelets for fault diagnosis of rotary machines： a review with applications[J]. Signal Process， 2014， 96(5)： 1-15.

[9]Ergin S， Uzuntas A， Gulmezoglu M B. Detection of stator， bearing and rotor faults in induction motors[J]. Procedia Engineering， 2012， 30： 1103-1109.

[10]Kumar H S， Pai P S， Sriram N S， et al. ANN based evaluation of performance of wavelet transform for condition monitoring of rolling element bearing[J]. Procedia Engineering， 2013， 64： 805-814.

[11]Ghods A， Lee H H. Probabilistic frequency-domain discrete wavelet transform for better detection of bearing faults in induction motors[J]. Neurocomputing， 2016， 188： 206-216.

[12]陈彦龙， 张培林， 李兵， 等. 基于能量聚集性的轴承复合故障诊断[J]. 噪声与振动控制， 2013(1)： 191-196. Chen Yanlong， Zhang Peilin， Li Bing， et al. Combined bearing fault diagnosis method based on energy aggregation[J]. Journal of Noise and Vibration Control， 2013(1)： 191-196. (in Chinese)

Feature Parameter Structure of Motor Bearing Fault Based on Wavelet and Cosine Transform

YUAN Ju-mei

( Dept. of Automation, Taiyuan Institute of Technology, Taiyuan 030008, China)

For the defects in application of the traditional characteristic parameters method of fault diagnosis, a new method based on the wavelet and cosine transform of characteristic parameter extraction was proposed to diagnose the bearing fault of induction motors. According to characteristics of vibration signals of the induction motor bearing, appropriate wavelet filter and information cost function were selected at first, and the vibration signals were decomposed into different frequency-domain subspaces. Then, the characteristic parameters of the bearing fault of induction motors were constructed by using the frequency domain energy aggregation of the discrete cosine transform, and the actual induction motoractual vibration signals of the induction motor bearing under normal, failure of inner, outer ring and ball bearing fault were analyzed. The analysis results verify that the constructed characteristic parameters can effectively achieve early detection and diagnosis of faults. At last, a comparison between the traditional characteristic parameters method and the proposed method was made, which states that the new method has better early diagnosis effects of bearing fault of induction motors.

wavelet packet; discrete cosine transform; fault diagnosis; motor; bearing

2016-09-27

山西省自然科学基金资助项目(2013011018-2)

原菊梅(1965-)， 女， 教授， 博士， 主要从事复杂系统建模与优化、 故障诊断的研究.

1673-3193(2017)02-0191-05

TP206.3

A

10.3969/j.issn.1673-3193.2017.02.017