基于离散元法的顺层岩质边坡的地震响应分析

江婷+沈振中+聂柏松+刘冲+谈家诚

摘要：基于离散元法，结合某水电站厂房后缘顺层岩质边坡工程，研究缓倾角多结构面岩质边坡的地震响应规律及锚杆的加固效果，提出了该边坡抗震加固优化方案。研究表明：未加固顺层块状岩质边坡在地震过程中位移呈現阶梯式增长，地震结束时刻边坡岩块松散崩落；加固后边坡位移显著减小，且能在地震作用下保持稳定；锚杆的剪力响应与其附近结构面的相对位移相关性强，表明锚杆附近岩层面间的相对位移是激发锚杆加固作用的主要因素，在坡面出露且出露点低的岩层面在地震作用下相对位移较大，对应的锚杆承受剪力也较大，据此可更合理地布置锚杆。

关键词：岩质边坡；结构面；离散元法；地震响应；锚杆；加固

中图分类号：TU 457 文献标识码：A 文章编号：1672-1683（2017）04-0136-06

Abstract：The seismic responses and anchor reinforcement effects of a bedding stereoplasm rock slope with multiple structural planes behind the powerhouse of a hydro-power plant by use of the DEM，and a optimal layout plan of the anchors is proposed.The research shows that displacements of the unreinforced bedding stereoplasm slope under seismic action is present the stepped increases，and the rock blocks fall at the end of earthquake.Displacements of reinforced slope diminish significantly，and the slope can remain stable in the earthquake.The shear force response of the anchor elements shows good agreement with the relative displacement response of the lay of terrain around the anchor element，which means that the relative displacement of the lay of terrain around the anchor is the main stimulation factor of the anchor reinforcement effects in the earthquake and the relative displacement of the lay of terrain emerging on slope surface and at a lower elevation is larger so that the shear force of the corresponding anchor is larger.Hereby this paper put forward the reasonable arrangement schemes of the anchor.

Key words：rock slope；structural plane；DEM；seismic response；anchor；strengthening

节理化缓倾角岩质边坡在水电工程中大量存在，地震诱发其失稳是影响水电工程建设顺利进行的关键问题[1-4]。加强对地震作用下边坡的动力响应研究，为边坡稳定进行预报预警提供力学理论依据，极具工程意义[5-8]。

岩质边坡位移的动力响应较为复杂，目前主要通过现场监测法、模型试验法和数值模拟法得到边坡位移动力响应。现场监测方法是最直接的方法，可信度高，但由于地震的不可预测性和监测周期长的原因，现场监测方法人力和物力成本较高。室内模型试验不必进行复杂全尺寸试验来获得真实试验成果，比较经济，但目前大多进行的是简单概化的模型试验研究，地质条件与加载条件较单一，无法精确模拟实际工程。数值模拟方法可以模拟分析复杂岩土体内部的响应现象和破坏机理，并把结果展示出来，因而许多工程中应用较多的是基于数值模拟方法来进行边坡位移动力响应的。数值模拟法主要有有限元法和离散元法等。例如张江伟[9]利用有限元法，基于强度折减法探讨了边坡在地震作用下的稳定性判定方法；彭宁波[10]等采用FLAC3D分析了波型以及振幅、及频率等地震参数对顺层岩质边坡的动力响应的影响；廖少波[11]等采用3DEC软件，基于离散元方法分析地震波在节理岩体中的传播特性，揭示地震作用对块状岩质边坡稳定性的影响机制；郑允[12]等采用UDEC软件提出一种计算爆破开挖时岩质边坡安全系数的节点拟静力法，提出利用最大节点位移时程曲线来判断边坡临界状态。

目前对岩质边坡的失稳判据已有了较深入的研究，一旦发现边坡存在失稳可能便要采取加固措施，而利用锚杆进行边坡治理是最常用的方法[13-15]，但如何合理有效地布置锚杆是加固设计的难题。本文基于离散元法，结合某水电站工程，应用通用离散元程序对地震作用下岩质边坡加固前后的动力响应进行研究，分析地震作用下加固与未加固边坡的位移状况以及锚杆的受剪情况，提出锚杆优化布置的建议。

[BT2+*8]1 离散元法动力计算模型

离散元法在连续介质力学的基础上，加入接触的概念，并将其作为连续体之间的边界，并采用连续力学方法描述连续体和接触的力学行为[16-17]。在UDEC模型中，把岩体定义为相互接触的块体的组合，块体代表岩体物理力学性质，接触代表结构面两侧块体间的相互作用。结构面的切向刚度较低，可不断地调整结构面的物理力学参数（如切向刚度、法向刚度、内摩擦角、黏聚力等）从而不断地改变结构面宏观物理力学性能，从而使模型不断地接近实际构造。

UDEC软件将岩体模型剖分成块体，将块体定义为可变形的，再讲块体划分为由有限差分的三角形单元组成的网格，在计算过程中单元各节点都是可以运动的。当研究区域的边界条件及作用力系改变时，一些块體将产生加速度并发生位移，块体的位置将改变，移动后的块体将与其周围的块体发生“叠合”，出现新的作用力系，随着力的传递，更多的块体发生位移。

1.1 差分网格构建

1.2 锚杆结构模拟

UDEC软件中采用cable单元[19]来模拟锚杆，即通过对锚杆、浆体和岩体单元边界的节点的相对位移，表示锚杆、灌浆体以及岩土体之间的相对滑动。在建模计算过程中，锚杆被分为许多双弹簧单元，弹簧1表述锚杆单元之间的拉拨力，弹簧2表述锚杆单元与砂浆间的黏结力，见图1。通过这些单元物理力学性质和位移可求出锚杆的变形情况和应力状态。

1.3 边界条件确定与地震波输入

固定边界会反弹地震波，而黏滞边界[20]是在模型边界施加法向阻尼器和切向阻尼器，阻尼器产生切向力和法向黏性力，将反射波引起的应力抵消，能够达到吸收入射波能量的目的。因此地震响应计算时须采用黏滞边界。

在地震响应计算前须对地震波进行基线校正和滤波处理。基线校正是在原始地震波时程上加入一个低频的多项式函数波型，使动力计算结束后模型速度和加速度为零。滤波处理是滤掉地震波中的高频部分，因为通过功率谱分析发现输入地震波的低频部分的能量占了地震波总能量的绝大部分，而且离散化的介质存在能量传播的上限频率，只有当输入的荷载频率小于这个上限频率时计算结果才有意义。

2 工程实例

2.1 地质工程概况

某水电站主厂房后缘边坡，开挖后形成高约30 m的顺层块状岩质边坡。根据工程地质勘察报告可知，一级、二级和三级边坡的倾角分别是72°、53°和72°，由倾角为56°的连续等距岩层面组和倾角为146°的不连续等距节理组切割形成块状边坡。该边坡具备有该类边坡的一般特点，即岩性单一，边坡结构面主要是层面和节理，节理的间距与层厚成正比，层面结合程度较好，在地震作用下可能发生局部崩塌性破坏，危及厂房安全。根据边坡工程地质情况和可能的破坏型式以及锚杆布置情况，在对其合理简化的基础上，建立如图2所示的剖面。岩体和结构面物理力学参数见表1和表2。工程中采用全长粘结式砂浆锚杆，其布置间距为2.5 m，锚杆布设角度和长度见表3，锚杆物理力学参数见表4。岩体材料采用理想弹塑性模型，破坏准则为M-C准则，采用面接触的Coulomb滑动模型模拟边坡的结构面和节理面。

在地震过程中，未加固顺层块状岩质边坡的监测点位移在3～5 s、9～10 s、14～16三个时间段突增，其他时间段保持平稳，呈现阶梯式增长，这说明位移具有累积效应，边坡岩块崩落发生在岩块位移累积到一定值时，而不是地震加速度最大时。在地震结束时刻，一级边坡坡面岩块松散滑移崩落，部分已滑落到坡脚，边坡处于不稳定状态。一级边坡上的岩块易滑移崩落，是因为在地震过程中，岩块所处位置越低处，所处位置为潜在滑动面时滑动体积越大，越易滑动。由分析可知，该边坡需进行加固。

2.3 加固后边坡的动力响应特性

2.3.1 边坡位移响应分析

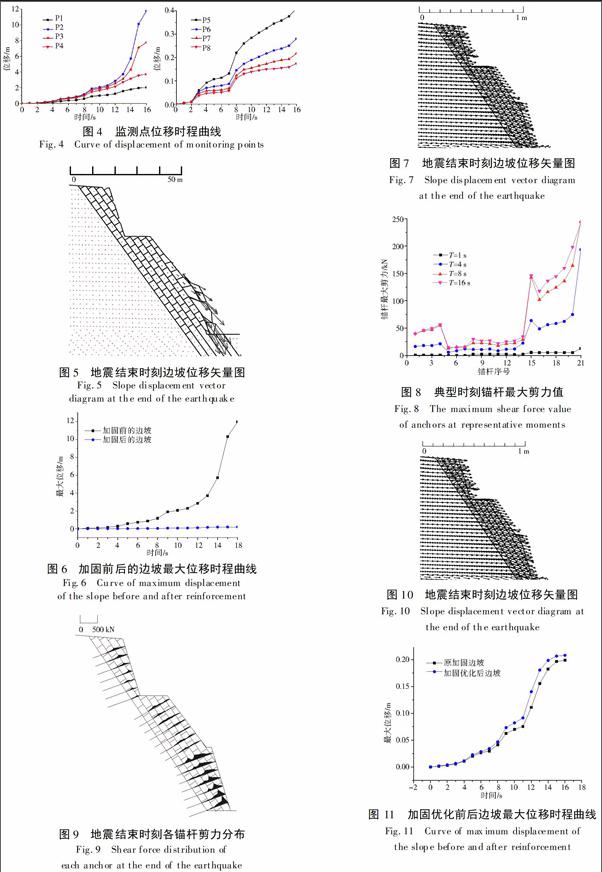
UDEC能够记录边坡在地震过程中任意时刻下位移最大的节点的位移值，加固前后的边坡最大位移时程曲线见图6，加固后地震结束时刻边坡单元节点位移情况见图7。

全长粘结式锚杆与周围岩体有很大的粘结刚度，能承受很大的轴向拉拨力，使锚杆在地震过程中不发生滑脱。在地震结束时刻，加固前边坡发生破坏，其最大位移值达到11.97 m，此时坡体的最大位[CM（22]移代表坡体岩块的最大滑落距离；加固后边坡坡面完好、未发生岩块滑落，最大位移为0.20 m，比未加固边坡减少了近98%，且最大位移曲线趋于平稳没有上升趋势。这表明锚杆加固效果显著，加固后边坡在地震作用下未发生破坏。

2.3.2 锚杆剪力分析

对于顺层边坡，全长粘结式锚杆的主要作用是阻止边坡岩体沿着层面滑动破坏，即抗剪作用大于抗拉作用，故本文重点分析锚杆的剪力。典型时刻各锚杆最大剪力时程曲线见图8，地震结束时刻锚杆剪力分布情况见图9，锚杆截面上的剪力对锚杆上任意一点矩为顺时针转向时为正，反之为负。

地震作用下，岩层面错动较大因此岩层面附近锚杆剪力较大。当锚杆穿过多个岩层面时，锚杆与在坡面出露的岩层面相交的部位剪力较大，且出露[CM（22]点越低剪力越大，因为出露点越低的岩层面为潜在滑动面时滑动体积越大，结构面相对位移越大。结合边坡的具体情况分析可知，第一级边坡的锚杆剪力最大，第三级边坡上锚杆剪力次之，第二级边坡上的锚杆剪力最小，这和计算结果相吻合。

2.4 加固锚杆布置优化

加固后边坡在给定的地震荷载下能保持稳定，但从岩层面对岩质边坡动力响应影响及加固后边坡的锚杆剪力分析来看，工程中所采用的加固措施可以适当优化，具体如下：

（1）第二级边坡坡度较缓，且坡面并无岩层面出露，锚杆的加固作用并没有充分发挥，地震结束时刻各锚杆最大剪力值也验证这个推论，第二级边坡的锚杆最大剪力仅为34 kN。因此，可考虑不在该级边坡布置锚杆；

（2）第三级边坡最下部3支锚杆所穿过的岩层面在整个边坡坡面均未出露，这三支锚杆的抗震加固作用也没有充分发挥，且地震结束时刻这3支锚杆的最大剪力仅为15.7 kN。因此，可考虑不布置编号为5、6、7的3支锚杆；

（3）对于第三级边坡最上部编号为1、2、3和4的4支锚杆，从地震结束时刻锚杆剪力值上看，最大剪力只有56，相对较小，但这4支锚杆均穿过了在第三级边坡坡面出露的岩层面，取消这4支锚杆可能会导致坡体沿岩层面滑动，所以不能取消布置这4支锚杆。

综上，取消布置编号为5～14的锚杆。

2.5 优化加固后边坡的动力响应特性

优化加固后地震结束时刻边坡单元节点位移情况见图6，优化加固前后最大位移时程曲线见图7。

在地震过程中，优化加固边坡未发生破坏，其位移和原加固边坡位移在方向和大小上基本保持一致。地震结束时刻优化加固后的边坡保持稳定，其最大位移时程曲线趋于稳定值，大小为0.21 m，仅比原加固边坡多了0.01 m。可判断优化加固方案与原加固方案效果相差不大，均能使边坡在给定地震荷载下保持稳定。

3 结论

对边坡进行地震响应过程模拟，有助于人们及时采取适当的加固措施，避免灾难发生。本文采用UDEC，针对某水电站厂房后缘顺层块状岩质边坡，计算分析了缓倾角多结构面复杂岩质边坡的动力响应规律及锚杆的加固效果。主要结论如下：

（1）离散元法能够很好地模拟含有岩层面、节理面等非连续结构面的岩质边坡的动力响应，即可以得到任何时刻下坡体与锚杆单元各节点的变形状态与应力状态，模拟出坡体渐进破坏的过程，其非连续性的破坏特征是有限元法等连续性方法所难以模拟的。

（2）基于该方法研究发现：未加固顺层块状岩质边坡在地震作用下，其破坏模式以一级边坡上局部岩块掉落为主，因为有岩层面出露且出露点低的坡面部位更可能发生岩块滑落。而加固后边坡能够在地震作用下保持稳定。穿过在坡面出露的岩层面的锚杆才能真正发挥作用，据此可优化锚杆的布置方案。

在其他工程中，岩质边坡的结构面分布形式多样，其破坏形式也很多。本文只是讨论了顺层块状岩质边坡加固前后的地震响应情况，而在其他结构面分布形式下的边坡稳定性则有待进一步研究。

参考文献（References）：

[1] 言志信，张森，张学东.地震边坡失稳机理及稳定性分析探讨[J].工程地质学报，2010，18（6）：844-850.（YAN Zhi-xin，ZHANG Sen，ZHANG Xue-dong .Failure mechanism and stability analysis of slope under earthquake[J].Journal of Engineering Geology，2010，18（6）：844-850.（in Chinese））

[2] 石崇，王盛年，刘琳.地震作用下陡岩崩塌颗粒离散元数值模拟研究[J].岩石力学与工程学报，2013，32（增1）：2798-2805.（SHI Chong，WANG Sheng-nian，LIU Lin.Research of avalanche disaster numerical simulation based on granular discrete element method of high-steep slope under seismic loads[J].Chinese Journal of Rock Mechanics and Engineering，2013，32（s1）：2798-2805.（in Chinese））

[3] 贺续文，刘忠，廖彪，等.基于離散元法的节理岩体边坡稳定性分析[J].岩土力学，2011，32（7）：2199-2204.（HE Xu-wen，LIU Zhong，LIAO Biao.Stability analysis of jointed rock slopes based on discrete element method[J].Rock and Soil Mechanics，2011，32（7）：2199-2204.（in Chinese））

[4] 宁宇，徐卫亚，郑文棠.应用离散元强度折减对复杂边坡进行稳定性分析[J].岩土力学，2007，28（增）：569-574.（NING Yu，XU Wei-ya，ZHENG Wen-tang.Application in complicated high slope with strength reduction method based on discrete element method[J].Rock and Soil Mechanics，2007，28（s）：569-574.（in Chinese））

[5] 刘天苹，李世海，刘晓宇.节理化岩质边坡随机结构面有限元和离散元耦合计算方法研究[J].岩石力学与工程学报，2014，33（增1）：3114-3122.（LIU Tian-ping，LI Shi-hai，LIU Xiao-yu.Study of dem and fem combination method for stochastic structural plane in jointed rock slope[J].Chinese Journal of Rock Mechanics and Engineering，2014，33（s1）：3114-3122.（in Chinese））

[6] He J M，Li S D，Yin Y P.Study of seismic response of colluvium accumulation slope by particle flow code[J].Granular Matter，2010，12：483-490 （10.1007/s10035-010-0213-8）.

[7] 杨国香，伍法权，董金玉.地震作用下岩质边坡动力响应特性及变[JP+2]形破坏机制研究[J].岩石力学与工程学报，2012，31（4）：696-702.（YANG Guo-xinag，WU Fa-quan，DONG Jin-yu.Study of dynamic response characters and failure mechanism of rock slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering，2012，31（4）：696-702.（in Chinese））

[8] 郑颖人，叶海林，黄润秋，等.地震边坡稳定性分析探讨[J].地震工程与工程振动，2010，30（2）：66-73.（ZHENG Ying-ren，YE Hai-lin，HUANG Run-qiu，et al.Study on the stability analysis of earthquake slope[J].Journal of Earthquake Engineering and Engineering Vibration，2010，30（2）：66-73.（in Chinese））

[9] 张江伟.土质边坡地震动力响应特牲分析及稳定性评价[D].北京：中国地震局地球物理研究所，2015（ZHANG Jiang-wei，Seismic dynamic response analysis and stability evaluation of soil slope[D].Beijing：Insititute of Geophysics，China Earthquake Administration，2015.（in Chinese））

[10] 彭宁波.锚固岩质边坡地震动力响应及锚固机理研究[D].兰州：兰州大学，2014.（Peng Ningbo，Study on seismic responses and anchoring mechanism of anchored rock slope[D]..Lanzhou：Lanzhou University，2014.（in Chinese）

[11] 廖少波.强震作用下块状岩体边坡稳定性研究[D].武汉：中国地质大学，2013.（LIAO Shao-bo.Study on stability of block rock slope under strong earthquake[D].Wuhan：China University of Geosciences，2013.（in Chinese）

[12] 郑 允 ，陈从新，朱玺玺，等.基于UDEC 的岩质边坡开挖爆破节点拟静力稳定性计算方法[J].岩石力学与工程学报，2014，33（增3）：3932-3940.（ZHENG Yun，CHEN Cong-xin，ZHU Xi-xi，et al.Node quasi-static stability analysis of rock slope underExcavation blasting based on udec[J].Chinese Journal of Rock Mechanics and Engineering，2014，33（s3）：3932-3940.（in Chinese））

[13] 叶海林，郑颖人，黄润秋，等.岩质边坡描杆支护参数地震敏感性分析[J].岩土工程学报，2011，28（9）：1374-1379.（YE Hai-lin，ZHENG Ying-ren，HUANG Run-qiu，et al.Sensitivity analysis of parameters for bolts in rock slopes under earthquakes[J].Chinese Journal of Geotechnical Engineering，2011，28（9）：1374-1379.（in Chinese））

[14] 吴月秀，刘泉声，卢海峰，等.UDEC 中Saeb-Amadei 节理本构模型的二次开发[J].岩石力学与工程学报，2012，31（增1）：3022-3030.（WU Yue-xiu，LIU Quan-sheng，LU Hai-feng，et al.Implementation of saeb-amadei model into user-definedjoint constitutive model in udec，[J].Chinese Journal of Rock Mechanics and Engineering，2012，31（s1）：3022-3030.（in Chinese））

[15] 高保彬，高佳佳，袁东升.基于UDEC 的大采高覆岩破裂的模拟与分析[J].湖南科技大学学报：自然科学版，2013，28（2）：1-6.（GAO Bao-bin，GAO Jia-jia，YUAN Dong-sheng.Simulation and analysis of overlying strata fracture in large mining height top-coal caving face of coal seams based on UDEC[J].Journal of Hunan University of Science & Technology：Natural Science Edition，2013，28（2）：1-6.（in Chinese））

[16] Eberhardt E，Stead D，Coggan J S.Numerical analysis of initiation and progressive failure in natural rock slopes-the 1991 Randa rockslide[J].International Journal of Rock Mechanics and Mining Sciences，2004，41：69-87（10.1016/S1365-1609（03）00076-5）.

[17] Bonilla-Sierra V，Scholtes L，Donze FV.DEM analysis of rock bridges and the contribution to rock slope stability in the case of translational sliding failures[J].International Journal Of Rock Mechanics And Mining Sciences，2015，80：67-78.

[18] Kuhlmeyer R L，J.Lysmer.Finite Element Method Accuracy for Wave Propagation Problems[J].soil Mech & Foundations Div，ASCE，1973，99：421-427（10.1007/s11803-013-0196-7）.

[19] Itasca Consulting Group Inc.Theory and background[Z].Minnesota：Itasca Consulting Group，2002.

[20] Cundall P.A.UDEC-A generalized District Element Program for Modeling Jointed Roc[Z].European Research Office，U.S.Army.1980.

[21] SL203-97.水工建筑物抗震設计规范[S].（SL203-97.Code for seismic design of hydraulic structures.（in Chinese））