基于精细积分法的轴承-拉杆转子系统非线性动力学分析

黑棣，郑美茹

（陕西铁路工程职业技术学院 机电工程系，陕西 渭南 714000）

轴承-转子系统作为旋转机械的核心部件，广泛应用于航天、电力、工程等领域。许多学者针对轴承-转子系统的相关问题进行了研究。文献［1-2］研究了表面织构对滑动轴承性能的影响。文献［3］求解了Reynolds方程，并且得到油膜压力分布曲线，分析了各种参数对油膜力的影响。文献［4］利用变分原理和分离变量法求得了油膜力的近似解析解。

以上研究都是为了能够更准确地进行轴承-转子系统的动力学分析。因为系统的稳定性直接决定旋转机械运行的稳定性，因此，轴承-转子系统动力学分析计算十分关键，最常用的轴承-转子系统动力学计算方法有Runge-Kutta法［5-6］、Wilson-θ法［7-8］、Newmark法［9-10］等，但均对计算步长的依赖较大。

精细积分法对步长的依赖较小，而且能保证较高的精度。文献［11］基于2N类算法提出了精细积分法。文献［12］将Wilson-θ法和精细积分法结合分析了结构地震时程反应。文献［13］给出了单步4阶精度的精细积分法，该方法精度高，计算量小。文献［14］采用改进的精细积分法计算了转子系统的非线性动力学行为。文献［15］将数据库方法与精细时程积分法相结合，研究了可倾瓦轴承-转子系统的动力学响应。

现基于改进的精细积分法，将其与传统的Wilson-θ法、Newmark法进行比较，求解转子系统的非线性动力学响应，研究步长对转子系统的非线性动力学行为的影响。

1 转子系统运动方程

拉杆转子系统模型如图1所示。图中：O1和O2为2个圆盘的中心；mO1，mO2分别为两圆盘的质量；eO1，eO2分别为两圆盘的偏心量；l为转轴的总长；a和b为两转轴的长度；AO1＝a1，BO1＝b1，AO2＝a2，BO2＝b2；ma，mb分别为 AO，BO的集中质量；fx和 fy分别为轴承处x，y方向上的油膜力。

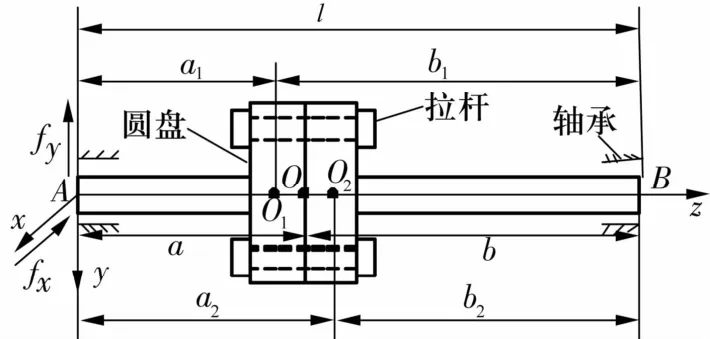
图1 轴承-拉杆转子系统示意图Fig.1 Sketch of bearing-rod fastening rotor system

式中：M为质量矩阵；G为陀螺矩阵；K为刚度矩阵；F为非线性油膜力向量；FAx，FAy-分别为轴承A处转子x，y方向的无量纲非线性油膜力；FBx，FBy-分别为轴承B处转子x，y方向的无量纲非线性油膜力；Q为外激励列向量；W为重力列向量；FR为圆盘间的非线性回复力；KR为量纲一的非线性回复刚度；Kb为拉杆量纲一的弯曲刚度。q为位移列向量；XA，YA，XO1，YO1，XO2，YO2，XB，YB分别为转子在轴承A端、圆盘O1处、圆盘O2处、轴承B端 x和 y方向的位移；θx1，θy1，θx2，θy2分别为圆盘1，2绕x和y轴的摆角；Jd1，Jd2分别为圆盘1，2的极转动惯量；Jz1，Jz2分别为圆盘1，2的赤道转动惯量；k11，k22分别为AO轴段x，y方向的弯曲刚度；k′11，k′22分别为 OB轴段 x，y方向的弯曲刚度；k33，k44，k′33，k′44分别为由于圆盘 1，2绕 x和 y轴摆动而引起的轴段刚度；k14，k23为AO轴段的交叉刚度；k′14，k′23为 OB轴段的交叉刚度，由于转子的对称性，有 k11＝k22＝k′11＝k′22，k33＝k44＝k′33＝k′44，k14＝k23，k′14＝k′［16］23；kR为非线性回复刚度；kb为拉杆的弯曲刚度。

2 改进的精细积分法

2.1 算法介绍

运用精细积分法求解转子系统的动力学响应，将（1）式化为

2.2 算法验证

为了验证该算法的有效性，针对以下算例，将其与Newmark法、Wilson-θ法进行比较。

分别采用3种算法进行计算，计算结果与精确解见表1。

由表1可以看出，文中方法的计算结果比Newmark法、Wilson-θ法更接近精确解。

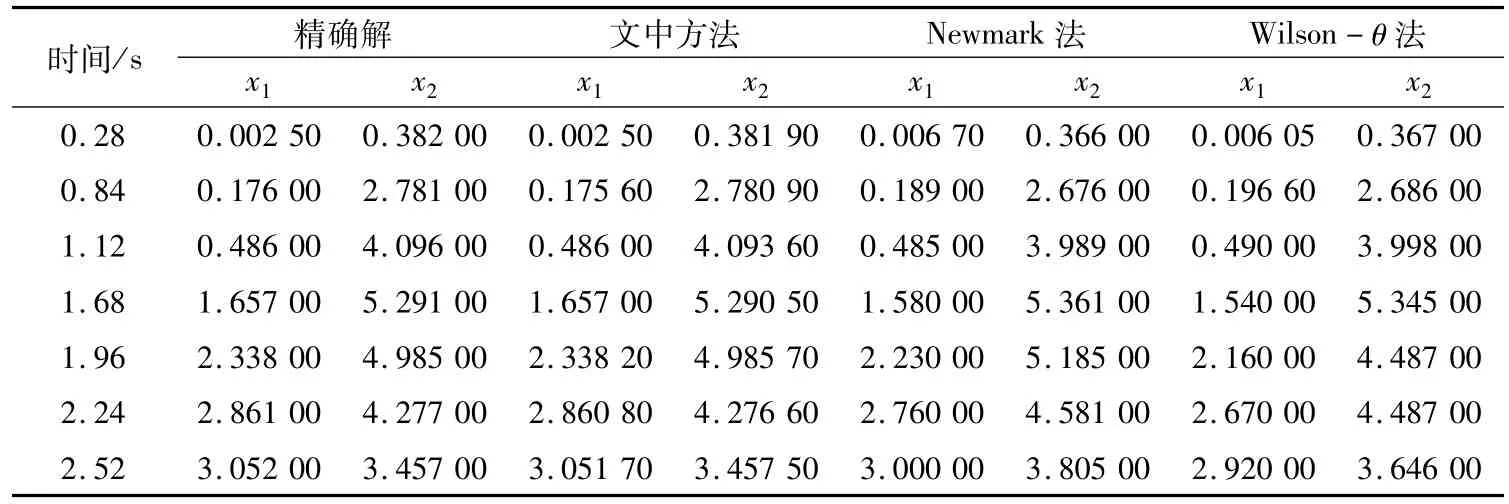
表1 3种方法计算结果Tab.1 Calculation results of three kinds of methods

3 数值算例

轴承-对称拉杆转子系统参数如下。轴承为360°径向滑动轴承，轴承宽度和直径之比D／d＝1，μ＝0.022 Pa·s，c＝0.000 49 m。转轴参数：r＝0.14 m，l＝3.3m，a＝1.6m，b＝1.6m，a1＝1.4 m，b1＝1.8 m，a2＝1.8m，b2＝1.4m，mA＝mB＝768.458 7 kg。圆盘参数：h＝0.4 m，R＝0.3 m，eO1＝eO2＝0.01c，mO1＝mO2＝690.044 5 kg，Jz1＝Jz2＝31.052 kg·m2，Jd1＝Jd2＝15.526 kg·m2。2m＝mA+mB+mO1+mO2，m＝1 458.5 kg。转轴刚度：k11＝k22＝k′11＝k′22＝9.992 5×107N／m，k14＝k23＝ -3.758 4×107N／m，k′14＝k′23＝3.758 4×106N／m，k33＝k44＝k′33＝k′44＝2.367 8×108N／m，kb＝kR＝2 k11。

以转子的量纲一转速为控制参数分析转子的非线性动力学行为，其计算步长为 h＝2π／200。当量纲一转速的变化范围为0.9～1.05时，转子轴承处和圆盘处y方向位移随转速的运动分岔图如图2所示。

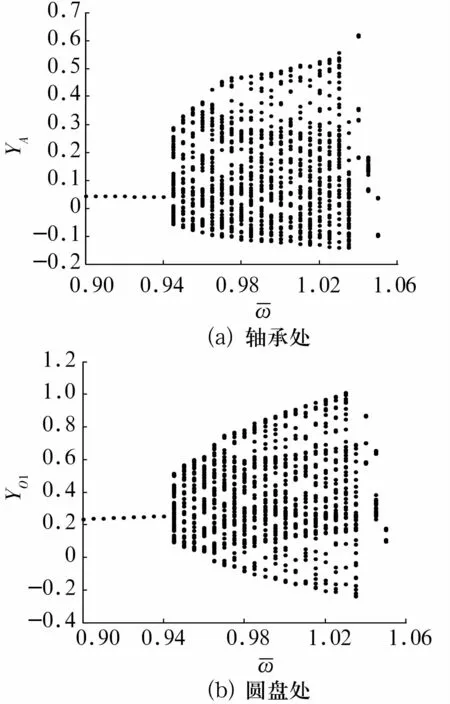
图2 转子轴承和圆盘处y方向位移随转速的运动分岔图Fig.2 Bifurcation diagram of y versus at bearing station and disk stations

由图2可以看出，转速较低时，转子系统的运动为周期运动，随着转速的升高，转子系统将发生分岔行为。

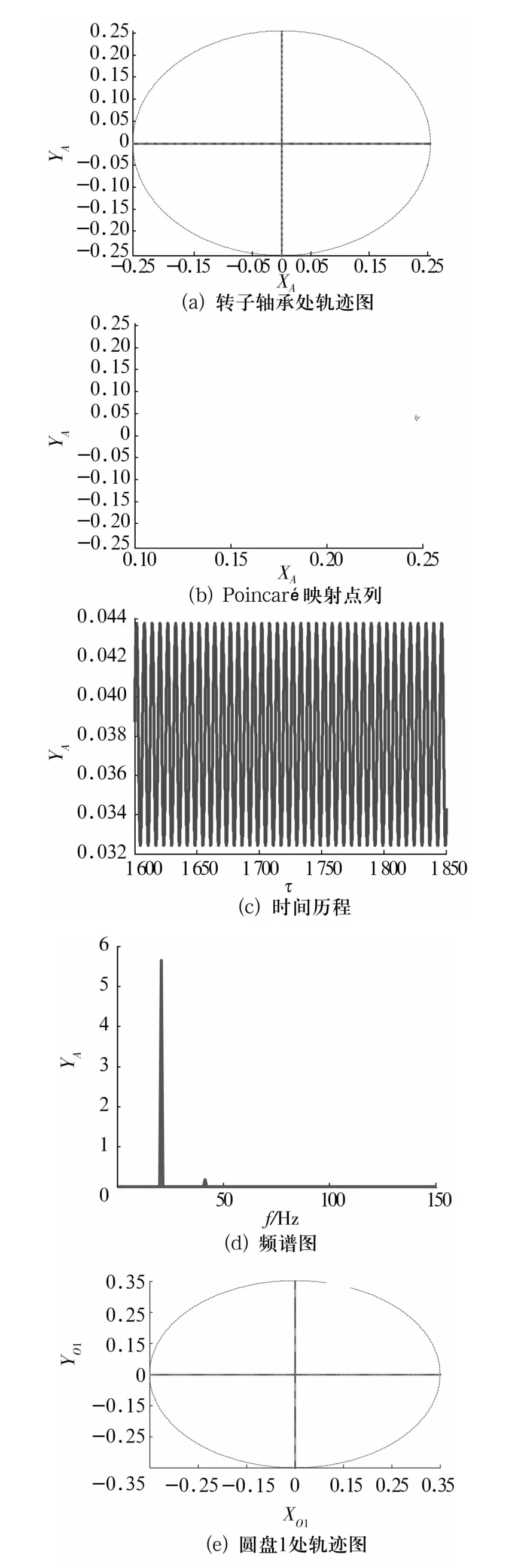
图3 ＝0.92时转子轴承处的轨迹图、Poincaré映射图、时间历程、频谱图和圆盘1处的轨迹图Fig.3 The orbit，Poincaré map，time series，spectrum of the rotor at bearing station and the orbit of disk 1 for＝0.92

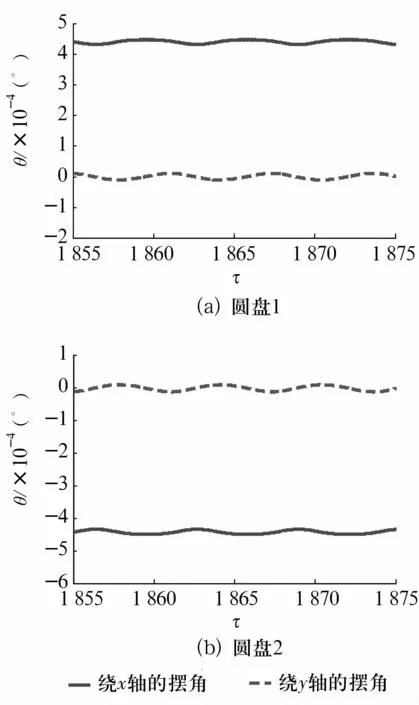
图4 ＝0.92时圆盘分别绕x，y轴的摆角Fig.4 The swing angle of disks around the x and y axis for＝0.92

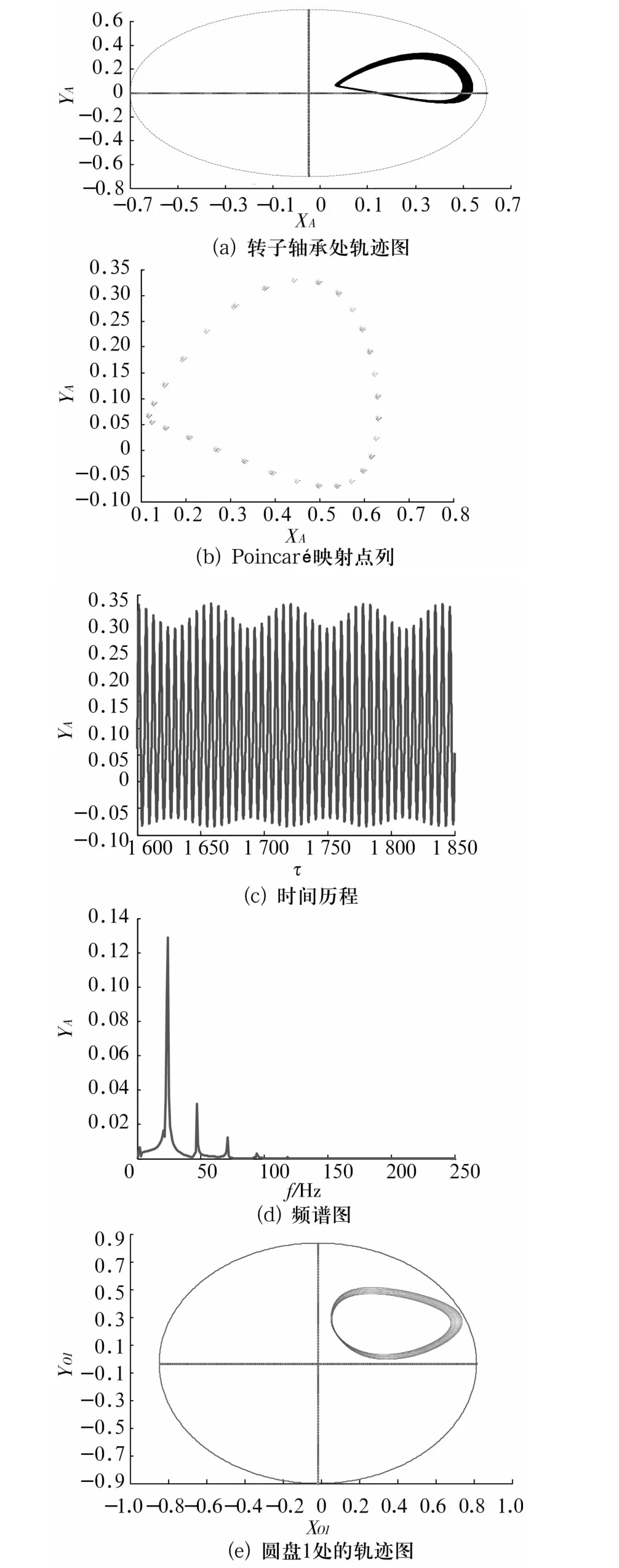
图5 ＝0.95时转子轴承处的轨迹图、Poincaré映射图、时间历程、频谱图和圆盘1处的轨迹图Fig.5 The orbit，Poincaré map，time series，spectrum of the rotor at bearing station and the orbit of disk 1 for＝0.95

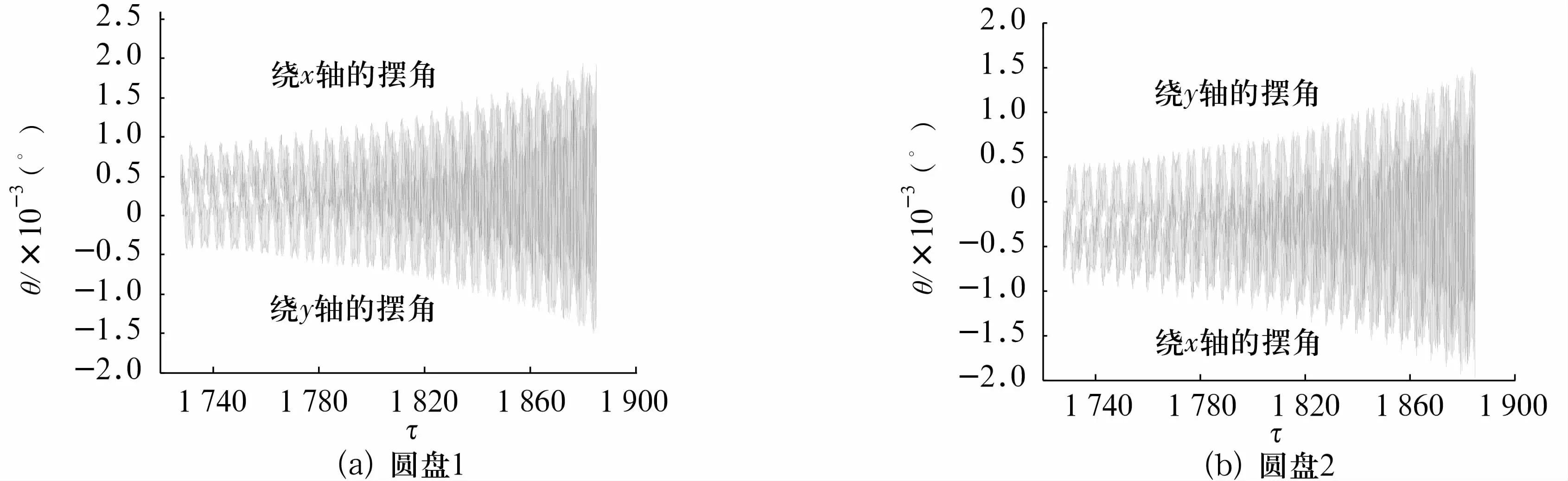
图6 ＝0.95时圆盘分别绕x，y轴的摆角Fig.6 The swing angle of disks around the x and y axis for＝0.95

图7 ＝1.04时转子轴承处的轨迹图、Poincaré映射图、时间历程和频谱图Fig.7 The orbit，Poincaré map，time series and spectrum of the rotor at bearing station for＝1.04

图8 ＝1.04时圆盘绕x，y轴的摆角Fig.8 The swing angle of disks around the x and y axis for＝1.04

以上计算步长取为h＝2π／200，为了研究计算步长对系统非线性动力学行为的影响，以下步长分别取为 h＝2π／400，2π／600，转子轴承处和圆盘处的分岔图如图9、图10所示。对比图2、图9和图10可知，转子系统运动的变化趋势基本相同，但分岔点有所不同，随着步长的减小，分岔点有少许增大，能够考察的转速范围也增大，且转子系统能够表现出更丰富的非线性动力学现象。由此可以看出，计算步长的变化对于转子系统运动具有一定影响。

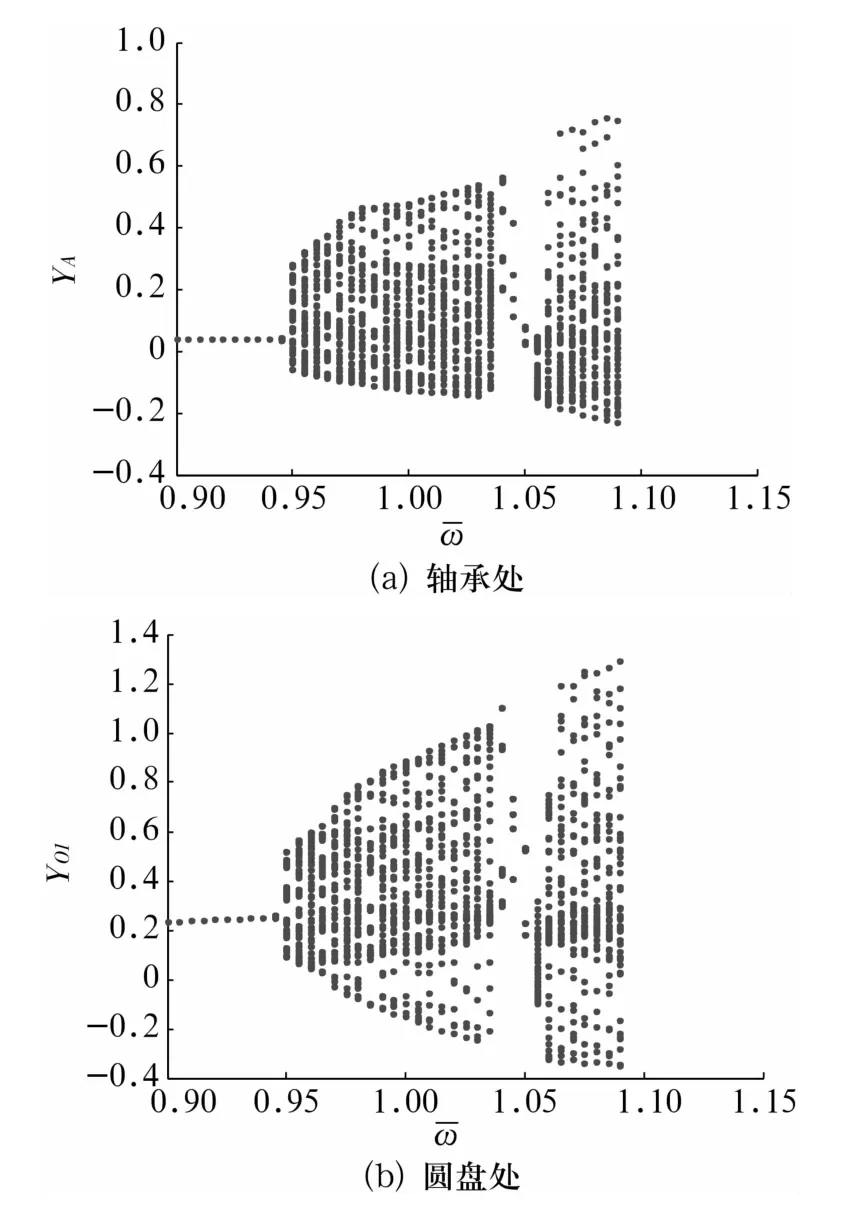
图9 h＝2π／400时转子轴承和圆盘处y方向位移随转速的运动分岔图Fig.9 Bifurcation diagram of y versus at bearing station and disk stations for h＝2π／400

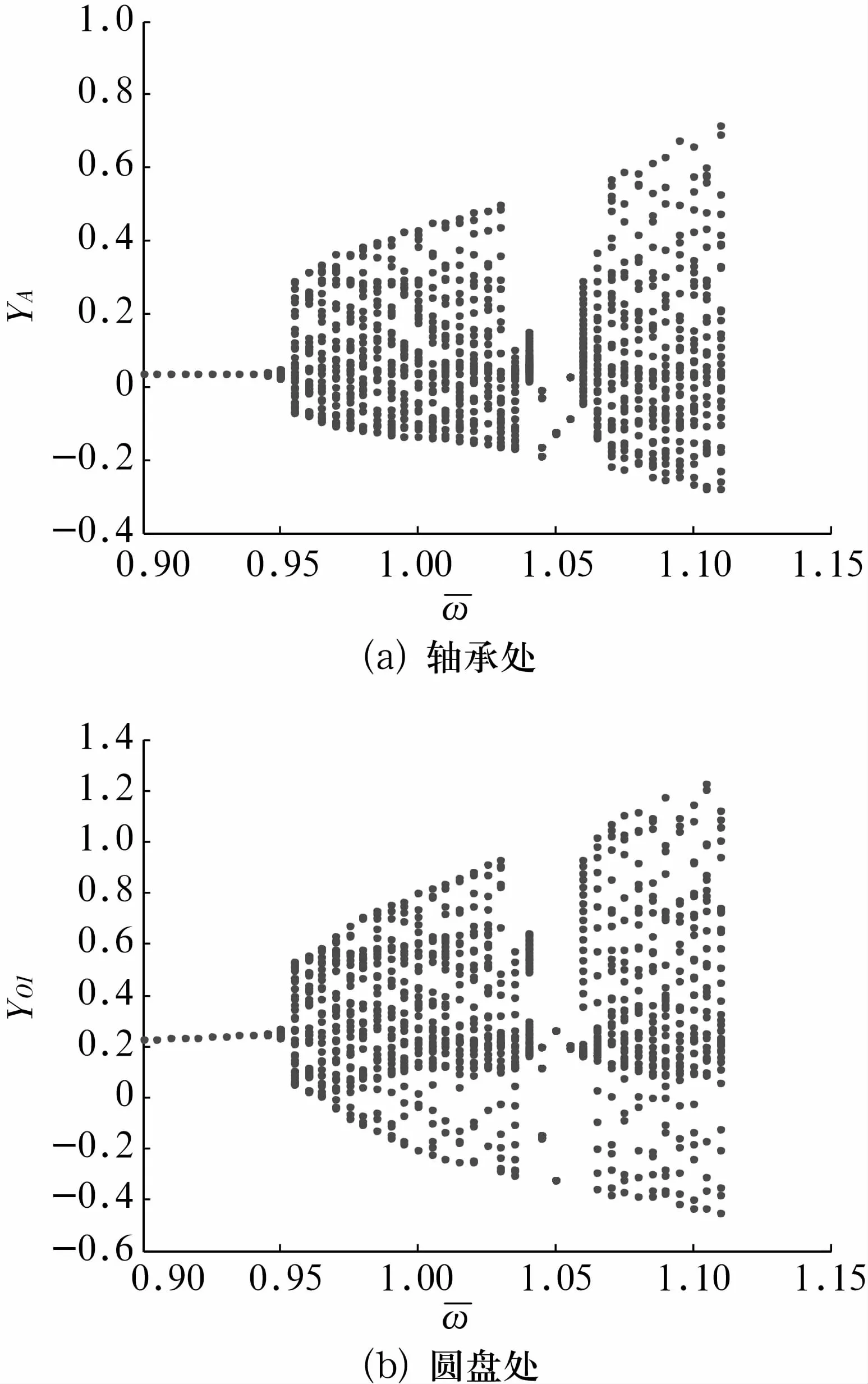
图10 h＝2π／600时转子轴承和圆盘处y方向位移随转速的运动分岔图Fig.10 Bifurcation diagram of y versus at bearing station and disk stations for h＝2π／600

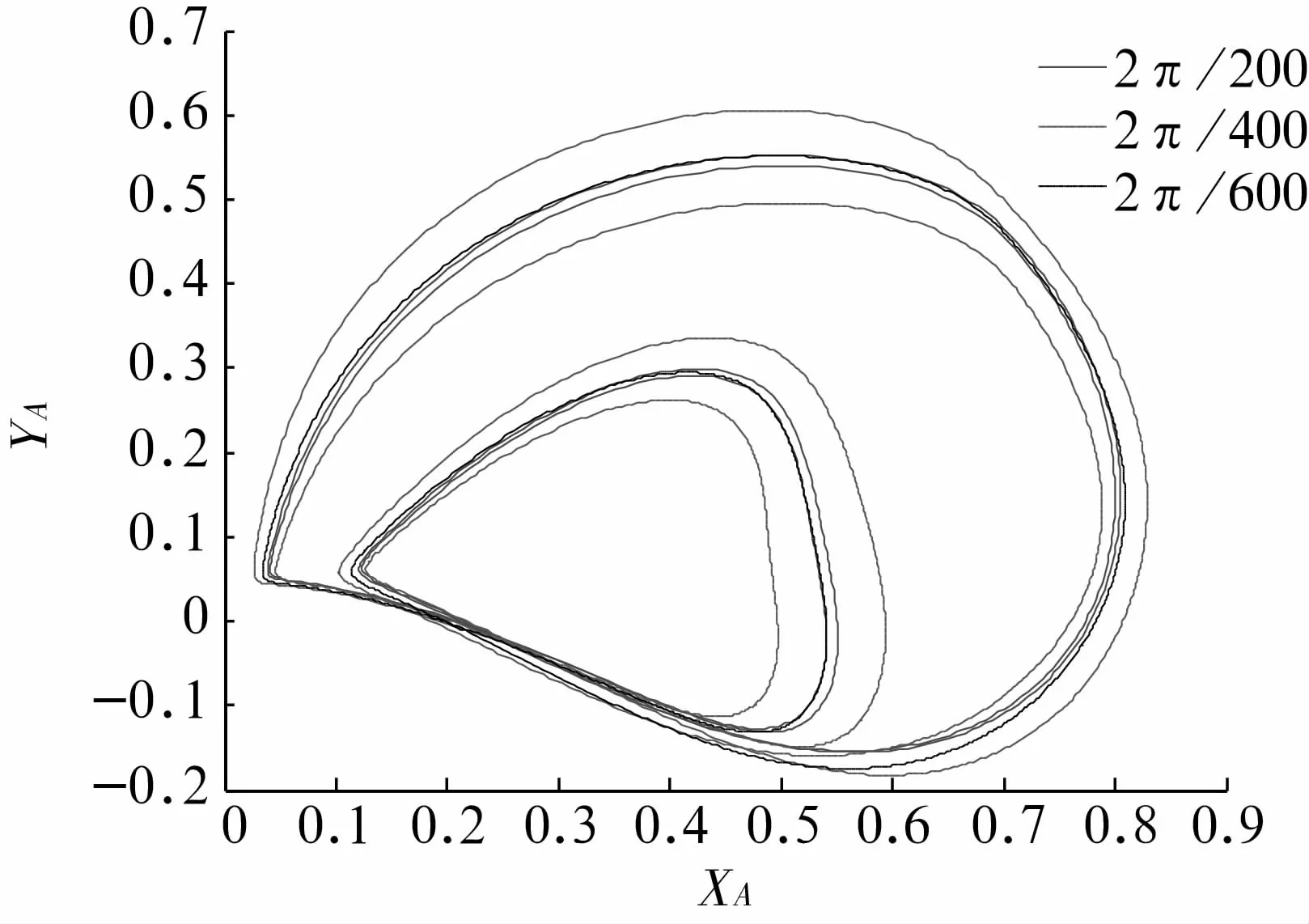
图12 ＝1.05时3种步长下轴承处轨迹Fig.12 Comparison between the three steps at bearing station for＝1.05

根据计算结果可以看出，计算步长对非周期运动影响较大，故从分岔点附近开始要缩小计算步长。在周期运动阶段，取不同的步长转子的运动轨迹有一定差别，但可以适当加大计算步长。

4 结束语

提出了一种改进的精细积分法，将其与常用的Newmark法、Wilson-θ法进行比较，发现该方法的计算结果比Newmark法和Wilson-θ法更接近精确解，验证了其可靠性。

运用改进的精细积分法计算拉杆转子系统的非线性动力学响应，从计算结果看出，该拉杆转子系统存在丰富的非线性运动现象。同时研究了拉杆转子圆盘的摆动，当转子系统处于准周期运动的情况下，圆盘的摆角随时间发散，最终导致转子碰壁。而其他情况下，圆盘的摆角均随时间呈周期性变化。

分析了计算步长对转子系统运动的影响，从计算结果可看出，计算步长对于转子系统非周期运动阶段的影响较大，故在非周期阶段应当采用较小的计算步长。在周期运动阶段，即使其他参数都相同，采用不同的计算步长，转子的运动轨迹仍有一定差别。计算步长对转子系统的影响有待进一步深入研究。