模型参考自适应PID控制在磁轴承中的应用

张建生，马啸宇，王一夫，章竹耀，吴璇

（1.南通大学 电气工程学院，江苏 南通 226019；2.常州工学院 电气与光电工程学院，江苏 常州 213002）

主动磁浮轴承系统（Active Magnetic Bearing System）利用电磁力使轴承转子稳定悬浮［1］，转子转速高、无机械磨损、无需润滑介质，系统可维护性高，维护成本较低。悬浮技术的应用条件相当苛刻，目前应用于军工、航天等重要领域［2］。主动磁悬浮轴承系统的数学模型表明其非线性且开环不稳定，需增加其他环节来实现转子稳定悬浮［1］。

常规PID控制因算法简单、参数整定困难及鲁棒性差等问题，难以达到对主动磁轴承转子的稳定悬浮控制要求。文献［3］采用改进的BP神经网络PID控制算法，找到某一最优控制规律下的PID参数，该算法有较强的非线性映射能力、自学习及自适应能力，但收敛速度慢、预测与训练能力有矛盾、从问题中选取典型样本实例组成训练集有很大难度。文献［4］在分析模拟PID控制器与数字PID控制器优缺点基础上，提出数模混合式PID控制器，使系统的响应速度及参数调节能力得到一定改善，但仍属于简单PID控制范畴，其固有缺点难以消除。文献［5］研究了模糊自适应PID控制，改善了系统的动、稳态性能，抗干扰能力及鲁棒性较强，但算法的模糊规则及隶属函数的建立完全凭经验且规则较难建立。为此，将模型参考自适应PID控制器应用到主动磁悬浮系统中，通过仿真分析验证其控制效果。

1 主动磁悬浮控制系统建模

单自由度主动磁悬浮控制系统原理如图1所示。系统中转子采用上、下电磁铁差动激励方式。图中：Ur为参考输入；Ul为信号调理电路处理位移信号值l后得到的电压信号；Uε为Ur与Ul的差值信号；Uc为控制器输出控制信号；I0为偏置电流；f1，f2分别为上、下电磁铁对转子的吸力；i为上、下电磁铁吸力变化导致的电流改变值；l为转子受到扰动导致偏离平衡位置的距离。

图1 单自由度主动磁悬浮控制系统原理图Fig.1 Principle diagram of active magnetic bearing control system with single degree of freedom

采用文献［3-7］中的差动激励方式建模，得到系统的开环传递函数为［8］

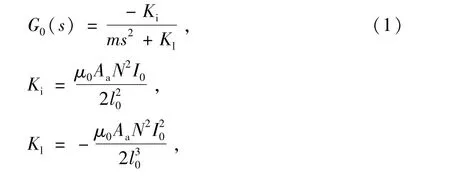
式中：Ki为电流刚度系数；Kl为位移刚度系数；μ0为真空磁导率；Aa为气隙面积；N为线圈匝数；I0为偏置电流；l0为平衡点位置。令（1）式分母为零，发现有一正根存在，根据Routh判据判定系统为开环不稳定系统［2，9］。

2 模型参考自适应PID控制器

2.1 控制系统组成

将模型参考自适应PID控制算法应用到主动磁悬浮轴承系统中，控制系统结构框图如图2所示。

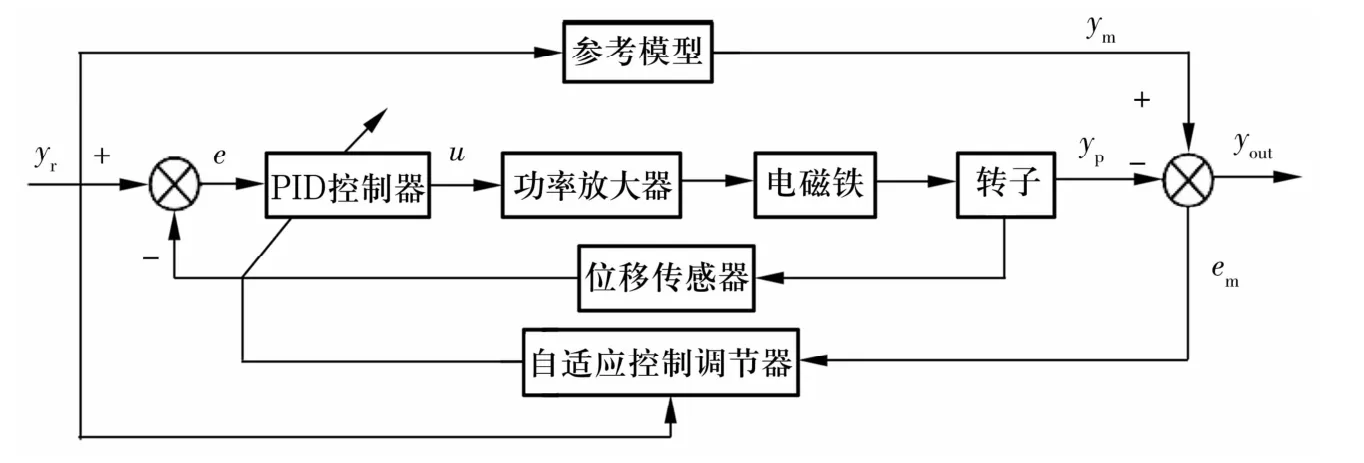
图2 主动磁悬浮轴承模型参考自适应PID控制系统结构框图Fig.2 Structure diagram of reference adaptive control system for active magnetic bearing model

图2中：yr为转子初始稳定悬浮位置；yp为转子的实际位置；ym为转子实现稳定悬浮的理论参考位置；e为转子从初始稳定悬浮位置相对实际位置的偏差信号；em为自适应控制误差信号；u为模型参考自适应PID控制器的输出信号；yout为系统输出响应。控制器以转子所在位置与初始稳定悬浮位置间的位移偏差作为控制输入信号，根据算法建立的参考模型与系统开环传递函数模型比较得到自适应控制误差，再驱动自适应调节器调整PID控制器参数kp，ki，kd，以不断减小系统误差，得到的控制信号通过改变上、下电磁铁线圈中的电流大小来调整转子的位置，使转子能够稳定悬浮。

2.2 控制算法推导

根据单自由度主动磁轴承系统模型，以上、下电磁铁中输出电流i作为输入量，以悬浮转子受扰动发生偏移经位移传感器检测后获得的输出电压Ul为输出量，得到主动磁轴承系统的输入输出开环传递函数为

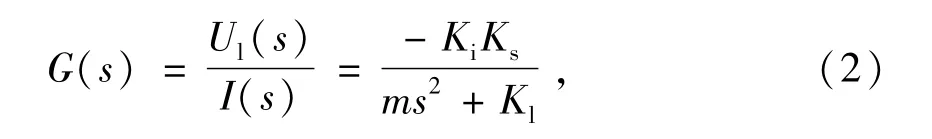
式中：Ks为位移传感器增益。由（2）式可知，开环传递函数的相对阶为2，故根据模型参考自适应PID控制算法设被控对象的系统状态方程［10-11］为

式中：xp为n维状态向量；u为控制量；yp为输出量；Ap为n×n矩阵；bp，hp为n×1向量。

根据（2）式和（3）式建立主动磁轴承输入输出传递函数为

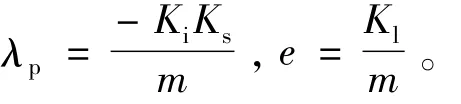
根据被控对象开环传递函数结构，选取磁悬浮轴承系统参考模型为

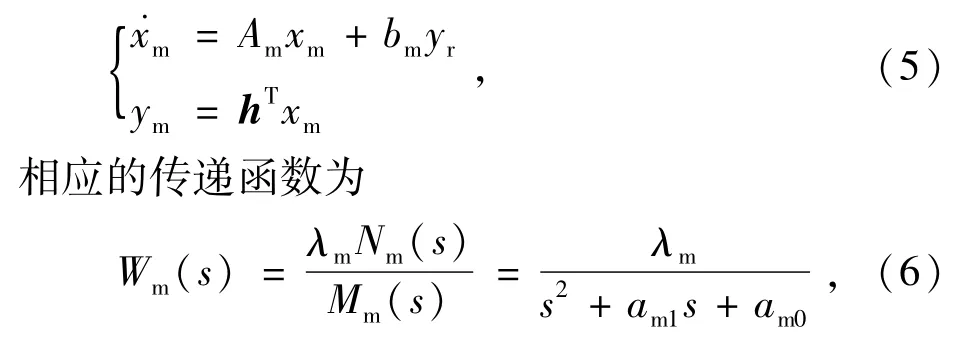
式中：Nm（s）＝1，λm＞0为参考模型增益；am1，am0为多项式一次项及常数项系数。Wm（s）的选取应为稳定最小相位系统并且与Wp（s）阶数及相对阶相同，还要有理想的动态性能。Mm（s）和Nm（s）分别为n阶和m阶首项为1的Hurwitz多项式。

从（4）式、（6）式可知，被控对象及参考模型的传递函数相对阶均为2，故Wm（s）不具有正实性，为保证 Wm（s）严格正实，引入一个多项式P（s），使 P（s）Wm（s）严格正实，取

式中：d0为可调参数；cT＝［c1，c2，…，cn-1］，dT＝［d1，d2，…，dn-1］cT，dT为参数可调向量；S（s）为n-1阶首项为1的稳定多项式；C（s），D（s）为n-2阶多项式。

控制器以转子所在位置与初始稳定悬浮位置间的位移偏差作为控制输入信号，根据算法建立参考模型与系统开环传递函数模型比较得到自适应控制误差em，驱动自适应调节器调整PID控制器参数kp，ki和kd，以不断减小系统误差，再通过控制器的输出信号u改变上下电磁铁线圈中电流大小以调整悬浮转子悬浮位置，使转子实现稳定悬浮。增量式PID控制算法［11］为

3 系统仿真与分析

单自由度磁轴承悬浮系统试验平台如图3所示。相关参数：转子质量m＝12 kg，功率放大器增益 Ka＝3.5 A／V，电流刚度系数 Ki＝418.25 N／A，位移传感器增益 Ks＝5 000 V／m，位移刚度系数Kl＝-2.201 8×106N／m。单自由度主动磁悬浮轴承控制系统结构框图如图4所示。

图3 单自由度磁轴承悬浮系统试验平台Fig.3 Experimental platform of single degree of freedom magnetic bearing

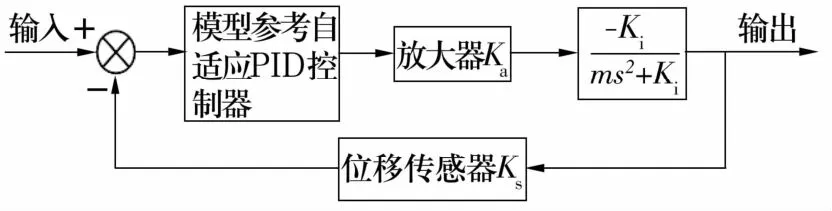
图4 单自由度主动磁悬浮轴承控制系统结构框图Fig.4 Control system structure of active magnetic bearing with single degree of freedom

利用MATLAB／Simulink进行系统仿真，以 C语言编写磁悬浮轴承系统的模型参考自适应PID控制算法［10-12］。未受扰动时的系统输出响应曲线如图5所示，PID控制器参数的整定曲线如图6所示。

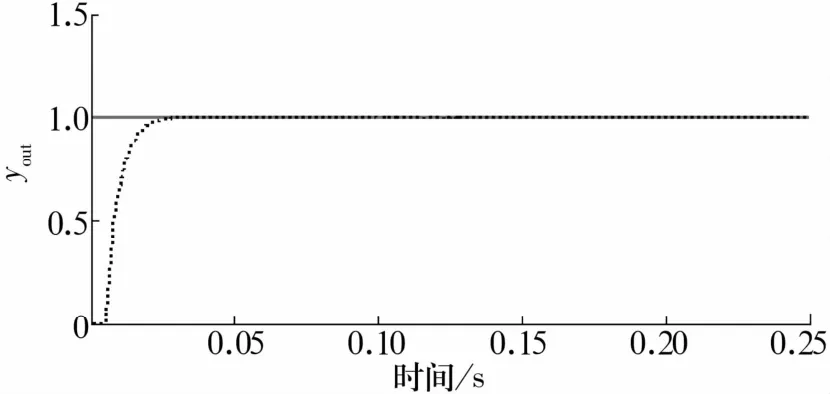
图5 未受到扰动时系统输出响应曲线Fig.5 Output response curve of system without disturbance

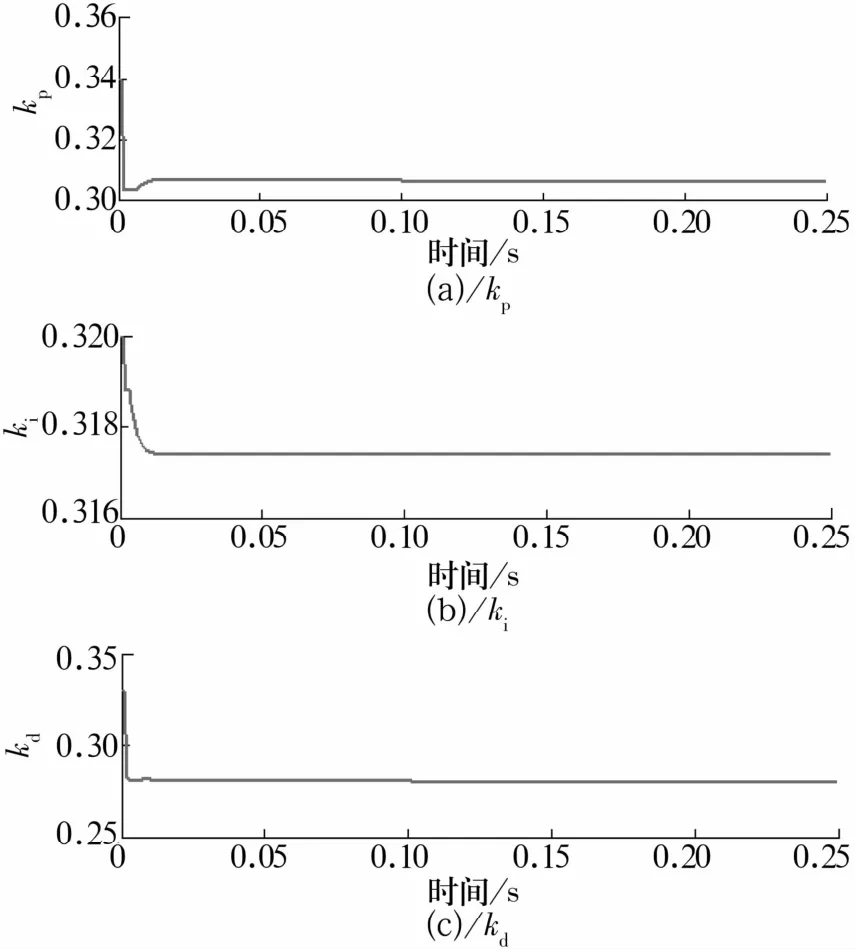
图6 PID参数整定曲线Fig.6 Tuning curve of PID parameters

由图5、图6可知，在无外部扰动情况下，磁悬浮轴承转子可实现稳定悬浮且几乎无超调，响应速度快，调节时间ts≈0.03 s。系统的动态性能、稳态性能均较好，此时得到控制器kp，ki，kd的整定参数分别为0.31，0.318，0.28。在 t＝0.1 s时给系统一个扰动信号，系统输出响应曲线如图7所示。经过约0.02 s干扰信号被抑制，转子回到稳定悬浮位置，证明系统具备抗干扰能力。

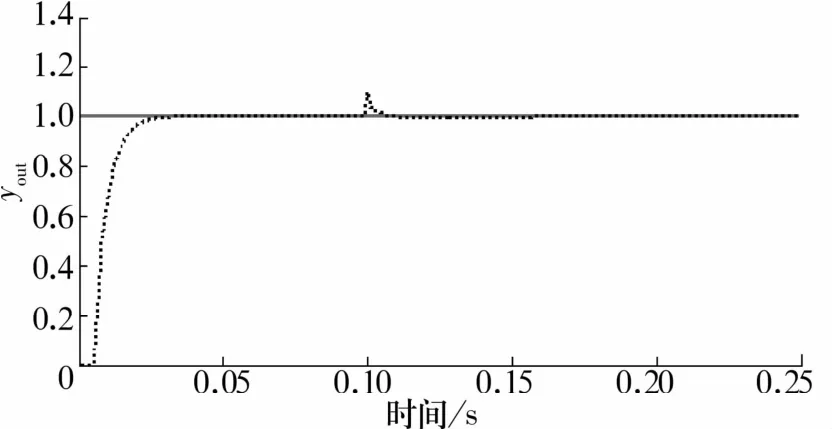
图7 受到扰动时系统输出响应曲线Fig.7 Output response curve of the system when the system is disturbed

常规PID控制算法与模型参考自适应PID控制算法都能达到使转子稳定悬浮的目的。与常规PID控制算法相比，模型参考自适应PID控制算法系统输出响应速度更快，超调量小，调节时间短，系统动、稳态性能更好（图8）。

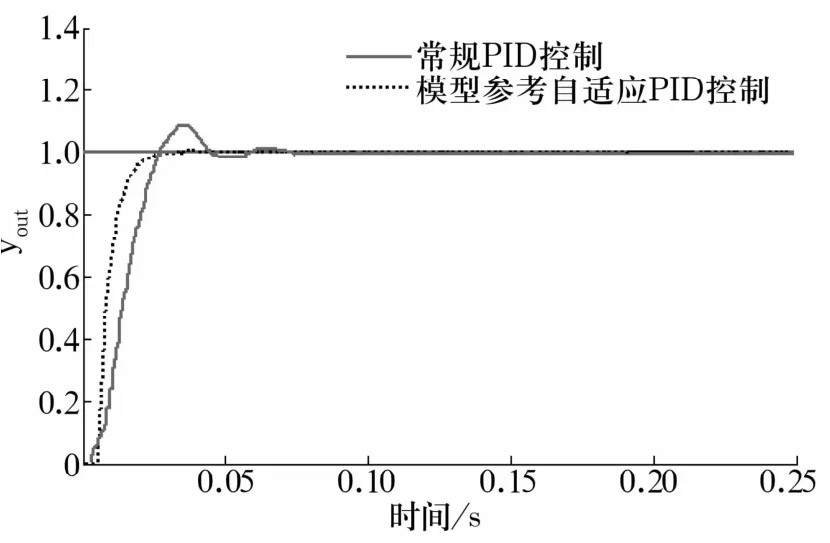
图8 2种控制算法下系统输出响应曲线对比Fig.8 Comparison of output response under two kinds of control algorithm

4 结束语

常规PID控制因算法简单、参数整定困难及鲁棒性差等问题，难以达到对主动磁轴承转子的稳定悬浮控制要求，限制了其在高精度控制系统中的应用。模型参考自适应PID控制通过参考模型与被控对象的比较，在线整定控制参数，使转子实现稳定悬浮，在有扰动情况下系统具有较强的抗干扰及恢复能力，控制效果优于常规PID控制。