一种新型轮毂轴承外圈结构的淬火有限元分析

2017-07-25李明磊邓凯文邓四二康乃正

轴承 2017年1期

李明磊，邓凯文，邓四二，康乃正

（1.河南科技大学机电工程学院，河南洛阳 471003；2.浙江兆丰机电股份有限公司，杭州 311232）

轮毂轴承套圈的淬火工艺可以使材料的性能显著提升［1］，但在淬火过程中伴随着不同程度的残余应力和变形，套圈的尺寸变化不均匀或尺寸的稳定性下降会导致后续的磨削工序中出现加工困难［2-3］。因此，研究减少淬火过程产生的残余应力与变形的方法，对于企业指导生产有着重要意义。

国内外众多学者对热处理淬火工艺的数值模拟技术开展了广泛的研究。文献［4］推导了轴承钢球的热传导方程，采用Bessel函数给出了热处理过程中钢球瞬态温度分布的解答，对钢球应力分布进行了分析。文献［5］采用ANSYS软件对20CrMoH直齿轮进行2种介质下表面淬火过程的有限元模拟，得到了淬火过程中的温度场、热应力与热变形等结果。文献［6］利用DEFORM软件模拟了渗碳淬火工艺对轮齿残余应力分布和变形量的影响，并研究了不同淬火温度对轮齿残余应力、变形及抗疲劳性能的影响规律。文献［7］利用有限元分析方法模拟了2A02合金叶片锻件经淬火处理后残余应力的分布，并选用模压冷变形处理消减残余应力。文献［8］将相变塑性引进计算模型，研究了不同材料的圆柱形试样在淬火过程中残余应力的分布，并与试验测定的应力分布进行了对比。目前大多数研究集中在对试样进行热处理仿真，而根据热处理仿真结果对试样结构进行改进的研究很少。

利用DEFORM有限元仿真软件对某型号轮毂轴承外圈的淬火过程进行仿真，研究不同结构参数下轮毂轴承外圈的应力／应变场，提出一种新型轮毂轴承外圈的结构。

1 淬火过程的有限元模型

1.1 淬火过程的数学模型

轮毂轴承外圈淬火过程是一个非稳态导热过程，运用能量守恒原理可推导出轮毂轴承外圈的导热微分方程，其表达式为

式中：λ为材料的导热系数；T为轴承套圈的瞬态温度；ρ为材料的密度；q为组织相变时产生的相变潜热；t为过程持续时间；cp为定压比热容。

在实际热处理过程中，轮毂轴承外圈加热到一定温度保温一段时间，以确保试件奥氏体化，此时可认为

式中：T0为炉内温度，即试件淬火初始温度。

淬火过程中总应变可由增量理论求解，淬火应变需要考虑热应变、组织应变和相变塑性应变的综合作用，即

式中：εt为热应变；εe为弹性应变；εp为塑性应变；εtr为相变应变；εtp为相变塑性应变［10］；βIJ为相变由I相向J相发生时所产生的单位方向上的体积变化量（即相变膨胀系数）；ξIJ为组织体积分数；δIJ为克罗地克系数；KIJ为I相到J相的相变塑性系数；S为偏张力。

1.2 有限元模型

轮毂轴承外圈的材料采用GCr15钢，成分和热物理性能参数分别见表1、表2。

表1 GCr15钢的化学成分（质量分数，%）Fig.1 Chemical component of GCr15 steel

表2 GCr15钢的热物理性能参数Fig.2 Thermo-physical property parameters of GCr15 steel

轮毂轴承外圈有限元模型如图1所示，其两端较薄，中部较厚，壁厚不均匀。由于轮毂轴承外圈的对称性，为简化数值模拟过程，取试件的四分之一进行有限元建模。对轮毂轴承外圈采用四面体网格划分方法，模型划分为85 934个单元，19 538个节点。其轮廓和尺寸如图2所示，其中外圈宽度B、沟曲率半径R、外径D、沟道直径 de分别为 36.25，6.86，82.40，75.25 mm。

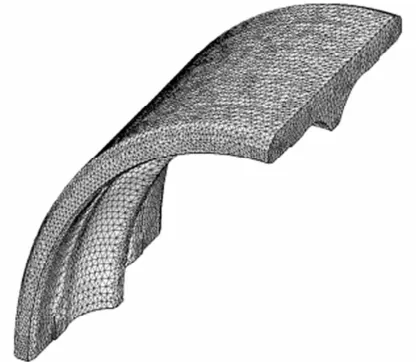
图1 轮毂轴承外圈的有限元模型Fig.1 The finite element analysis model of outer ring of hub bearing

图2 轮毂轴承外圈结构Fig.2 Structure of outer ring of hub bearing

2 淬火过程模拟结果分析与讨论

2.1 轮毂轴承外圈淬火后的应力与变形分析

使用的热处理工艺为：轮毂轴承外圈在工业热处理炉中加热至840℃，保温6～8 min，经传送带快速运送至30℃的循环油池中冷却，再运送至清洗室进行清洗。借助DEFORM有限元仿真软件求解轮毂轴承外圈淬火过程的瞬态应力／应变场。

淬火后轮毂轴承外圈的等效应力分布与径向变形情况分别如图3、图4所示。在淬火工序后，轮毂轴承外圈内外径均略有膨胀，且外圈外表面中部的膨胀量比两端大，沟道膨胀量也较大。这是因为在淬火过程中，试件温度逐渐降低使得热膨胀逐渐消除，取而代之的是马氏体相变引起的体积膨胀。淬火初期，两端的冷却速度比中部快，故两端壁厚收缩较快，到达马氏体转变温度后，两端首先形成马氏体，继而是厚壁表面和心部形成马氏体，由于马氏体形成的不同时性，使得两端马氏体能够相对地自由膨胀，限制中部材料沿轴向的延伸，同时，试件中部本身较厚，体积膨胀量也相对较大，所以导致中部的膨胀量比两端大。

图3 淬火后轮毂轴承外圈的等效应力分布Fig.3 Effctive stress distribution of outer ring of hub bearing after quenching

图4 淬火后轮毂轴承外圈的径向变形情况Fig.4 Radial deformation of outer ring of hub bearing after quenching

由图3可知，外圈外表面中部的残余应力最大，分析原因后，决定采用2种外圈结构对其等效应力和变形进行研究，如图5所示。在外圈外表面中部开槽，槽的设计原则为尽量使外圈壁厚一致。为了便于研究淬火后不同槽深的轮毂轴承外圈结构的等效应力分布，在工件上取外圈沿轴向方向路径AB和外圈滚道路径CD进行分析，如图6所示（外圈壁厚的截面图）。

图5 轮毂轴承外圈开槽后的三维模型Fig.5 3D modeling of hub bearing ring after slotting

图6 轮毂轴承外圈横截面上的路径AB和路径CDFig.6 The path AB and CD at section of hub bearing ring

2.2 不同结构轮毂轴承外圈的应力分析

由于在后续加工过程中或者实际使用过程中会打破工件内部残余应力的平衡状态，相应部位的弹性变形也会发生变化，从而引起工件尺寸的变化，所以，残余应力会对工件的变形以及尺寸稳定性产生较大的影响。

淬火后轮毂轴承外圈表面等效应力随槽深变化的规律如图7所示。由图可知，矩形槽0.6 mm深时的最大等效应力达到260 MPa左右，随着槽深的加大，最大等效应力也逐步下降，并且深度越深，外圈外表面中部的应力峰越尖，说明在开槽部分应力仍然分布不均匀；弧形槽0.6 mm时的最大等效应力达到250MPa左右，比矩形槽略低，随着槽深的加大，最大等效应力急剧减小，1.8 mm槽深时最大等效应力只有85 MPa左右，明显低于矩形槽1.8 mm槽深时的最大等效应力。同时，弧形槽部分的等效应力分布较为均匀，几乎没有应力峰，因此弧形槽结构1.8 mm深时的等效应力分布较好。

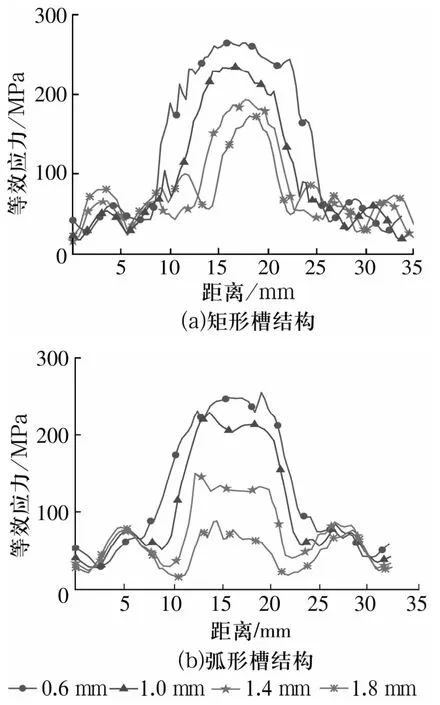
图7 表面路径AB的等效应力随槽深变化曲线Fig.7 The effective stress of hub bearing on surface at path AB

淬火后轮毂轴承滚道处等效应力随槽深变化的规律如图8所示。由图可知，滚道处的等效应力随着槽深的加大而减小，弧形槽滚道处的等效应力在同样槽深处要小于矩形槽。

图8 滚道处路径CD的等效应力随槽深变化曲线Fig.8 The effective stress of the hub bearing on raceway at path CD

综上所述，弧形槽由于其应力分布均匀，同时相同槽深时应力小于矩形槽，所以弧形槽结构效果更佳。

2.3 不同结构轮毂轴承外圈的变形分析

马氏体在淬火过程中，由于工件各部位的冷却速度不均匀，出现热应力和组织应力相互作用从而导致零件变形。导致工件变形的因素有：工件的形状和尺寸、原始组织的均匀性、淬火前的粗加工状态（车削时进刀量的大小、机加工的残余应力等）、淬火时的加热速度与温度、工件的摆放方式、入油方式、淬火介质的特性与循环方式、介质的温度等［11］。

不同矩形槽深的轮毂轴承外圈径向变形情况如图9所示。由图可知，槽深0.6 mm时，外圈外表面中部的变形明显比两端的大。槽深1.0～1.8 mm时，中部变形较为均匀，两端变形较大。这是由于槽深越大，滚道处的壁厚越薄，导致其冷却速度大于两端冷却速度。淬火初期，滚道薄壁处的冷却速度比两端快，故滚道薄壁处收缩较快，到达马氏体转变温度后，滚道处首先形成马氏体，继而是两端部表面和心部形成马氏体，由于马氏体形成的不同时性，使得滚道处马氏体能够相对自由地膨胀，限制两端部材料沿轴向的延伸，同时，试样两端本身比滚道处厚，体积膨胀量也相对较大，所以两端的膨胀量比中部大。

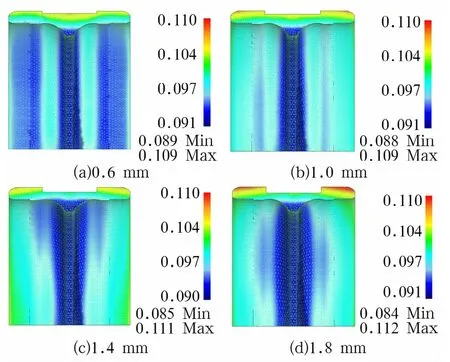
图9 不同矩形槽深的轮毂轴承外圈径向变形Fig.9 The radial deformation of hub bearing ring with different depths of rectangular groove

不同弧形槽深的轮毂轴承外圈径向变形如图10所示。由图可知，当槽深达到1.8 mm时，整个外圈的壁厚趋于一致，变形程度也趋于一致，达到0.11 mm，因此外圈的外径膨胀均匀，变形情况优于矩形槽结构，可以为机加工余量的确定提供指导。而滚道处的径向变形几乎没有变化，均在0.10 mm左右，说明外圈外表面结构的改变对滚道处的径向变形几乎没有影响。