极限状态条件下边坡喷锚结构冻融破坏分析★
2017-07-24毕全超张铭修王学蕾
毕全超 张铭修 王学蕾 饶 强
(河北建筑工程学院,河北 张家口 075000)
极限状态条件下边坡喷锚结构冻融破坏分析★
毕全超 张铭修 王学蕾 饶 强
(河北建筑工程学院,河北 张家口 075000)
针对混凝土喷层与坡体分离的脱粘现象,通过力等效原理对喷层自身的重力进行分解,并结合圣维南原理,提出了三种破坏假设并进行了分析计算。结果表明:在喷层与坡体完全脱粘的极限状态条件下,喷层厚度不宜过大;当采取喷锚支护措施时,应综合考虑混凝土局部压碎和钢筋受剪断裂两种情况。
喷锚支护,冻融循环,承载极限,脱粘现象
0 引言
我国是一个多山国家,随着交通事业的迅猛发展,在工程建设中大多数边坡需要采用支护措施以保证安全。喷锚支护作为一种最为常见的边坡治理措施,其原理是锚杆(索)、混凝土喷层和岩土体三者共同形成受力体系。该体系可以防止岩土体松动、分离,喷射的混凝土能侵入周围岩土体裂隙、封闭节理、加固结构面和层面,提高岩土体的整体性并抑制变形的发展,从而提高边坡的稳定性[1-6]。
喷锚支护作为用于边坡加固的一种常用形式广泛应用于工程实践中,而随着水分的迁移及其在三相之间的转换,会出现混凝土喷层与坡面脱粘的现象,并导致支护结构破坏。对喷锚结构进行极限状态分析,控制混凝土喷层的合理厚度,对实际工程的安全具有重要的意义。
1 锚杆受力分析
以一土质边坡为例,假设其坡角α,锚固角β,锚杆间距m,锚杆直径d,喷层厚度n,喷射混凝土的体积密度ρ,其范围为2 200 kg/m3~2 300 kg/m3。
假设混凝土喷层与坡面脱粘但锚固系统未被破坏,相当于混凝土喷层悬挂于锚杆上,造成锚杆需承受所有来自喷层自身的重力。由于锚杆均布布置,所以以单根锚杆作为单元体,分析受力。对于依附于锚杆上的混凝土,按照面积均匀分割考虑,如图1所示。

对锚杆进行简单受力分析:
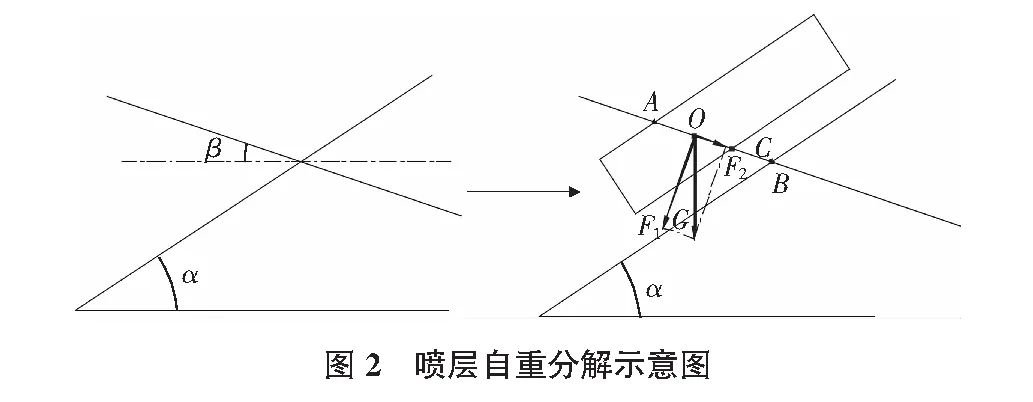
混凝土重力沿锚杆方向进行分解,分解为垂直于锚杆方向的力F1和平行于锚杆方向的力F2,如图2所示。
其中,各力大小如下:
G=m2·n·ρ·g
(1)
F1=G·sin(α+β)
(2)
F2=G·cos(α+β)
(3)
下面对破坏方式提出假设并进行受力分析和理论计算:
1)混凝土喷层因自重过大,与锚杆接触面的上部混凝土局部压碎;
2)在钢筋与混凝土接触面,钢筋受剪断裂,喷层滑落垮塌;
3)混凝土喷层沿锚固角方向滑移。
2 针对极限状态假设的理论分析与计算
2.1 混凝土局部压碎假设
混凝土喷层的重力全部传递给锚杆,可能造成与锚杆接触面上部混凝土局部压碎。根据圣维南原理,若假设成立,只可能是混凝土与钢筋的接触面的局部混凝土被压碎。
单根锚杆相当于受到面积为m2的混凝土重力影响,钢筋在混凝土喷层中的长度为L,钢筋与混凝土喷层的有效接触面积为:
S=n·d/sin(α+β)
(4)
混凝土单元体的重力:
G=m2·n·ρ·g
(5)
只有垂直于锚杆方向的力F1对锚杆有剪切作用,所以剪切力的值为:
V=F1=G·sin(α+β)
(6)
接触面混凝土压应力:
(7)
由上式可知,接触面混凝土压应力与喷层厚度n无关,而与坡角α、锚固角β和锚杆间距m成正比,与锚杆直径d成反比。计算结果如表1所示。
由表1可以得出:锚固角对混凝土的受压作用影响较小,而坡角和锚杆间距对混凝土的受压作用影响较大,若采用18 mm的螺纹钢作为锚杆,锚杆间距不宜超过5 m。若坡角较缓,可适当增大锚杆间距。
2.2 钢筋受剪断裂假设
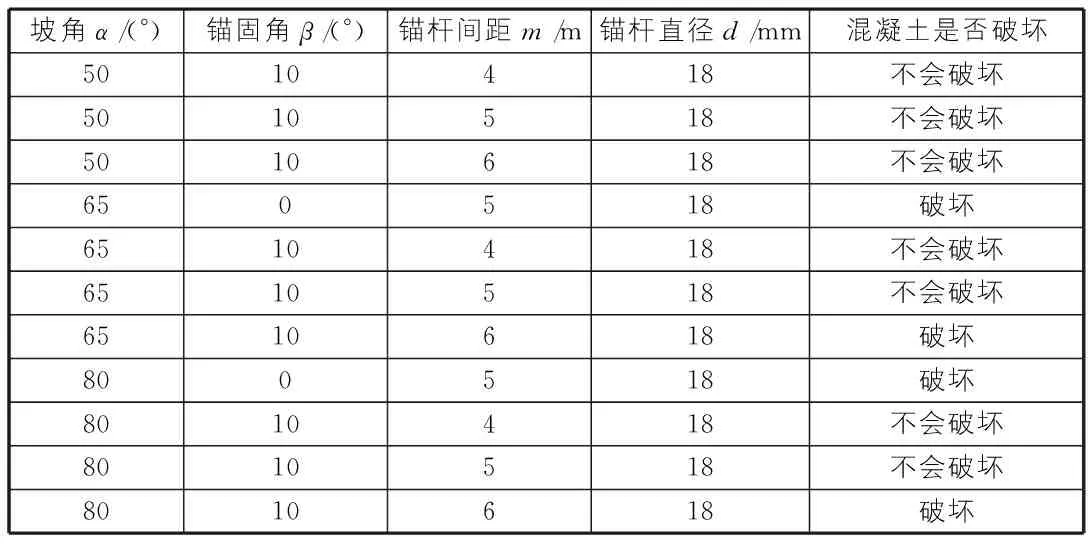
表1 混凝土受压计算
针对钢筋在与混凝土接触面受剪断裂的假设进行钢筋受剪分析,根据剪切公式τ=V/A判断剪力最大的接触面所在位置。剪切公式中,钢筋的截面面积A(查规范可得)一定。在AC段(不包括C点),部分混凝土的重力对钢筋有剪切作用;C点处,受全部混凝土重力影响,钢筋所受的剪力最大,为V=Vmax,即最大剪力作用面为C点所在的钢筋截面。
钢筋所受剪力为:
(8)
由式(8)可得,在钢筋处于极限抗剪状态时,喷层的最大厚度可表示为:
(9)
由式(9)可知,钢筋所受剪力与坡角α、锚固角β、锚杆间距m、喷层厚度n成正比,与钢筋截面面积A成反比。选用Q235钢筋的极限抗剪强度进行计算,计算结果如表2所示。

表2 喷层厚度计算结果
由表2可以得出:
1)锚固角、锚杆间距、锚杆直径一定的情况下,随着坡角的增大,喷层厚度的极值逐渐减小,且减小的趋势越来越缓;
2)坡角、锚杆间距、锚杆直径一定的情况下,随着锚固角的逐渐增大,喷层厚度的极值逐渐减小,几乎呈均匀下降趋势且趋势稳定但影响很小;
3)坡角、锚固角、锚杆直径一定的情况下,随着锚杆间距的逐渐增大,喷层厚度的极值急剧减小且趋势越来越缓;
4)坡角、锚固角、锚杆间距一定的情况下,随着钢筋直径增大,喷层厚度的极值逐渐增大,且增长趋势越来越大;
5)综上所述,喷层厚度极值与几个因素都有关,当坡角为60°,锚杆倾角为10°,钢筋直径为18 mm,锚杆间距为4 m时,在钢筋的极限抗剪强度情况下,喷层厚度极大值取用94 mm。若锚杆间距较大时,应适当增大选用钢筋直径。
2.3 混凝土喷层沿锚固角滑移假设
针对锚杆沿锚固角滑移的假设,对锚杆沿锚固角方向进行受力分析,如图3所示。
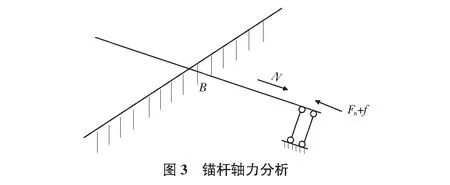
在上面所述的受力分析中,沿锚固角方向的力为F2;Fn是锚杆的杆端承载力;f是锚杆的侧摩阻力。
N=F2=G·cos(α+β)=m2·n·ρ·g·cos(α+β)
(10)
若Fn+f 若Fn+f=N时,沿锚固角方向混凝土喷层不会发生滑移; 因为Fn和f是被动力,Fn+f不可能大于N。 经上述分析可得,混凝土喷层可能会沿锚固角方向发生滑移,但不会破坏。若混凝土喷层会沿着锚固角方向发生滑移,直至混凝土喷层贴合边坡,喷锚系统达到稳定状态,不会破坏;初始时,喷锚系统就已经稳定,不会产生滑移,不发生破坏。 本文通过力等效原理把喷层自身的重力进行分解,并结合圣维南原理,提出了混凝土局部压碎、钢筋受剪断裂、混凝土喷层沿锚固角方向滑移三种假设并进行了受力分析和理论计算,结果表明,在假设喷层与坡体完全脱离的极限状态下: 1)接触面混凝土压应力与喷层厚度n无关,而与坡角α、锚固角β和锚杆间距m成正比,与锚杆直径d成反比; 2)钢筋所受剪力与坡角α、锚固角β、锚杆间距m、喷层厚度n成正比,与钢筋截面面积A成反比; 3)锚固角对混凝土的受压作用和喷层厚度均影响较小,而坡角和锚杆间距对两者的影响都较大; 4)混凝土喷层可能会沿锚固角方向发生滑移,但不会破坏; 5)当采取喷锚支护措施时,应综合考虑混凝土局部压碎和钢筋受剪断裂两种情况。 [1] 杨玉川,杨兴国,邢会歌,等.基于传压原理的喷锚支护边坡稳定性分析方法[J].中国农村水电,2014(11):101-104,108. [2] 张伟勇.喷锚支护优点浅析[J].路基工程,2004(4):60-62. [3] 毕全超,王学蕾,张 韬,等.谈冻融循环下的边坡灾害及防治措施[J].山西建筑,2016,42(33):66-67. [4] 毕全超,王学蕾,董 捷,等.冻融循环影响下边坡锚固结构的受力分析[J].科技资讯,2017,15(1):57-60. [5] 胡居义,文海家,张永兴,等.高边坡喷锚支护及其可靠性预测[J].工程勘察,2004(6):1-3. [6] 湛 伟.浅析边坡支护中喷锚支护技术的应用[J].广东科技,2012(3):213-214. Analysis of frost-thaw failure of anchor-shotcrete retaining under limit state★ Bi Quanchao Zhang Mingxiu Wang Xuelei Rao Qiang (HebeiUniversityofArchitecture,Zhangjiakou075000,China) In this paper, the view of the phenomenon of concrete spraying and the peeling on the slope, the gravity of the concrete sprayed layer is decomposed by the force equivalent principle and combined with the Saint-Venant principle. Three kinds of assumptions and the stress analysis and theoretical calculation are carried out. The results show that the thickness of the spray layer should not be too large under the ultimate condition of the spray layer and the slanting body completely. When taking the anchor-shotcrete retaining measures, we should consider the local crushing of concrete and steel shear fracture two cases. anchor-shotcrete retaining, freeze-thaw cycle, bearing the limit, debonding phenomenon 1009-6825(2017)17-0061-03 2017-03-13★:河北省科技厅计划项目(编号:15275416);河北省教育厅青年基金(编号:QN2014136);河北建筑工程学院研究生创新基金(编号:XA201709);张家口市交通局项目(路堑边坡锚固结构在冻融循环下的力学行为及灾害预防研究,编号:16033) 毕全超(1981- ),男,硕士,副教授; 张铭修(1992- ),男,在读硕士 TV554.12 A3 结语
